Cite this Article
Wang Guang-Yi, Cai Bo-Zhen, Jin Pei-Pei, Hu Ti-Ling. Memcapacitor model and its application in a chaotic oscillator. Chinese Physics B , 2016, 25(1): 010503  
Permissions
Memcapacitor model and its application in a chaotic oscillator
Wang Guang-Yi †, , Cai Bo-Zhen , Jin Pei-Pei , Hu Ti-Ling
Key Laboratory of RF Circuits and Systems, Ministry of Education of China; Institute of Modern Circuits and Intelligent Information, Hangzhou Dianzi University, Hangzhou 310018, China

 

† Corresponding author. E-mail: wanggyi@163.com

Project supported by the National Natural Science Foundation of China (Grant Nos. 61271064, 61401134, and 60971046), the Natural Science Foundation of Zhejiang Province, China (Grant Nos. LZ12F01001 and LQ14F010008), and the Program for Zhejiang Leading Team of S&T Innovation, China (Grant No. 2010R50010).

Abstract
Abstract

A memcapacitor is a new type of memory capacitor. Before the advent of practical memcapacitor, the prospective studies on its models and potential applications are of importance. For this purpose, we establish a mathematical memcapacitor model and a corresponding circuit model. As a potential application, based on the model, a memcapacitor oscillator is designed, with its basic dynamic characteristics analyzed theoretically and experimentally. Some circuit variables such as charge, flux, and integral of charge, which are difficult to measure, are observed and measured via simulations and experiments. Analysis results show that besides the typical period-doubling bifurcations and period-3 windows, sustained chaos with constant Lyapunov exponents occurs. Moreover, this oscillator also exhibits abrupt chaos and some novel bifurcations. In addition, based on the digital signal processing (DSP) technology, a scheme of digitally realizing this memcapacitor oscillator is provided. Then the statistical properties of the chaotic sequences generated from the oscillator are tested by using the test suit of the National Institute of Standards and Technology (NIST). The tested randomness definitely reaches the standards of NIST, and is better than that of the well-known Lorenz system.

PACS : 05.45.–a ; 05.45.Jn ; 05.45.Pq
Keyword : memcapacitor ; oscillator ; chaos ; statistical test
1. Introduction

In 1971, Chua postulated the missing fourth circuit element which is named the memristor by using the functional relation between charge q and flux φ (d φ = M d q ). [ 1 ] Until 2008, an operational Chua memristor was finally realized by a team of researchers at Hewlett-Packard (HP) based on a thin film of titanium dioxide, [ 2 ] which has attracted immense worldwide interest from both industry and academia.

In 2009, Ventra, Pershin, and Chua extended the concept of the memrisor to memcapacitor and meminductor, which are defined by the charge–voltage relation and the current–flux relation, respectively. [ 3 ] These memory devices are common at the nanoscale, where the dynamical characteristics of ions and electrons are likely to depend on the histories of the systems that exhibit their memorability. [ 3 ] These nanoscale devices can store information without a power source, and their combination in circuits is likely to find new applications in non-volatile memory, and to simulate learning, adaptive, and spontaneous behaviors. [ 3 ] Therefore, the nanoscale memory device is becoming a new hot spot in research. [ 4 – 6 ]

In 2009, a piecewise model of the memcapacitor was presented in Ref. [ 3 ]. In fact, it has long been found that a nanoscale capacitor possesses a memory effect, and shows a capacitance–voltage or charge–voltage hysteresis characteristic, the examples include Ge nanocrystal embedded Hf-aluminate high- k gate dielectric [ 7 ] and metal oxide semiconductor structure containing nanocrystals deposited by ion-beam-assisted electron beam deposition. [ 8 ] Since then some systems with the memcapacitance property have been found, including vanadium dioxide metamaterials, [ 9 ] ionic memcapacitive effects in nanopores, [ 10 , 11 ] the analog memory capacitor based on field configurable ion-doped polymers, and the solid-state memcapacitive system with negative and diverging capacitance. [ 12 ] Especially, Ref. [ 13 ] proposed a bistable non-volatile elastic-membrane memcapacitor, which has two stable states, i.e., low and high capacitance configurations, and exhibits a chaotic oscillation with certain driven voltage amplitudes and frequencies.

Now as a memory device, the memristor has been widely studied in non-volatile memory, artificial neural networks, and nonlinear circuits such as chaotic oscillators. [ 14 – 20 ] However, compared with the memristor, the memcapacitor and the meminductor have been relatively little studied. Although actual solid-state memcapacitors and meminductors have not appeared yet, it is of significant importance to design effective equivalent models of these two elements and make prospective studies of their applications. [ 21 ]

References [ 22 ] and [ 23 ] presented piecewise linear and exponential 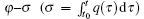characteristics, respectively, and also designed the corresponding chaotic oscillators. Fitch introduced a chaotic circuit with the memcapacitor model of cubic smooth φ – σ characteristic. [ 24 ] References [ 25 ] and [ 26 ] respectively proposed a SPICE model of parallel plate memcapacitor and a memcapacitor emulator. Reference [ 27 ] presented a memristor model on the basis of the LDR memristor model.

We propose an HP memristor-like memcapacitor model in this paper. The reason is that the properties of memristor, memcapacitor, and meminductor are common at the nanoscale level, and thus the HP memristor-like memcapacitor model conforms more to the future real memcapacitor. Based on the memcapacitor model, a circuit model for emulating the behaviors of the mamcapacitor is constructed, and on the basis of the memcapacitor circuit model, a memcapacitor oscillator is designed. Its dynamical behaviors are analyzed and verified by theoretical analysis and circuit experiments respectively. Some special phenomena and good randomness of the oscillator are found. Furthermore, an analog circuit and a digital circuit are designed for confirming the memrcapacitor oscillator. Finally, its statistical properties are tested by the NIST standards.

2. Memcapacitor model
2.1. Mathematical model of memcapacitor

Some studies have found that some micro systems can exhibit memcapacitor effects. Hence according to the model of the nanoscale HP memristor, we give a memristor-like model of the memcapacitor.

The memristance of the HP memristor can be written as [ 2 ]

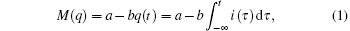
where a and b are coefficients related to the HP memristor, and q ( t ) and i ( τ ) are the charge and the current through the memristor, respectively.

Similarly, Chua defined the memcapacitor as a charge-controlled capacitor, and the relation between voltage u and charge q is described as [ 3 ]

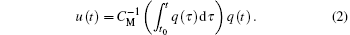
Considering Eqs. ( 1 ) and ( 2 ), we can define a charge-controlled memcapacitor from

where ( α + βσ ) is the inverse memcapacitance, i.e., ; and . By integrating Eq. ( 3 ) with respect to time t , the relation between flux φ ( t ) and σ is obtained as

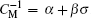
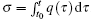
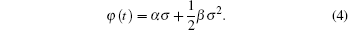
Let α = 0.7, β = 3.2, and q ( t ) = Q m sin(2 π ft ), the applied voltage (blue) and the resulting charge (green) are shown in Fig. 1(a) , where Q m = 0.5 C. When Q m = 0.5 C, Q m = 0.3 C, and Q m = 0.2 C, the corresponding u – q hysteresis curves are shown in Fig. 1(b) , and the σ – φ characteristic is shown in Fig. 1(c) .

Fig. 1. Characteristics of charge-controlled memcapacitor: (a) waves of voltage and charge, (b) voltage–charge hysteretic curves, (c) φ – σ curve.
2.2. Equivalent circuit of the memcapacitor model

Figure 2(a) shows the proposed circuit to emulate the properties of the memcapacitor described by Eq. ( 3 ). The voltage across resistor R1 is proportional to the input current, and so the input current can be sampled by R1. The output of instrument amplifier AD620AN is sent to the input port of the integrator consisting of operational amplifier U3B and capacitor C2, and the charge – q is obtained from the output of this integrator. When the – q is integrated again by the integrator consisting of OP amplifier U3A and capacitor C1, is obtained from the integrator. The output of multiplier A1 is βσq ( t ) as − q and σ are sent simultaneously to the input port of the multiplier. The voltage u ( t ) = ( α + βσ ) q ( t ) is obtained from the output of the adder consisting of U3C and R12.

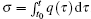
Fig. 2. Equivalent circuits for charge-controlled memcapacitor: (a) equivalent circuit of u – q characteristic, (b) equivalent circuit of φ – σ characteristic.

Figure 2(b) shows the equivalent circuit to emulate the φ – σ characteristic. The simulation results obtained by using Multisim are described in Fig. 3 .

Fig. 3. Characteristics of charge-controlled memcapacitor: (a) hysteresis u – q curve, (b) φ – σ characteristic.
3. Memcapacitor oscillator
3.1. Oscillator circuit

Based on Chua’s circuit and Ref. [ 24 ], a charge-controlled memcapacitor circuit is designed as shown in Fig. 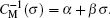4 , which consists of four linear elements and one charge-controlled memcapacitor with the proposed HP-memristor-like memcapacitance . The negative conductance − G provides energy for the circuit so as to maintain a continuous oscillation in the circuit.

Fig. 4. Oscillator circuit with charge-controlled memcapacitor.

By taking the current i L through the inductor, the voltage u c across the capacitor, and the charge q m on the memcapacitor as state variables, and by applying Kirchoff’s laws to this circuit, the state equations are obtained as

where u cm ( t ) = ( α + βσ m ) q m ( t ). As , equation ( 5 ) can be transformed into the following form:

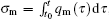
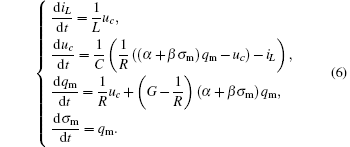
When L = 0.13 H, C = 3.57 F, R = 0.21 k Ω , G = 2.1 mS, α = 0.7 F −1 , and β = 0.8 F −1 ·C −1 ·s −1 , this memcapacitor oscillator exhibits a chaotic oscillation as shown in Fig. 5 . It is clear that all the circuit variables, i.e., the voltage u c across the capacitor C , the current i L through the inductor L , the charge q m through the mamcapacitor C M , and the voltage u cm across the memcapacitor C M , are chaotically evolving with time. The bifurcation diagram of current i L and the corresponding Lyapunov exponent spectrum with respect to parameter L are shown in Fig. 6 , from which we can see a novel and complex bifurcation process. The bifurcation of current i L from period-5 to period-6 emerges at 1/ L = 8.58; while at 1/ L = 8.64, the bifurcation from period-6 to period-3 occurs, and the bifurcation from period-3 to period-2 occurs at 1/ L = 8.79. In addtion, forward period-doubling and inverse period-doubling emerge simultaneously on each side of the period-6 window, 1/ L ∈ [7.98, 8.07]; and the forward abrupt chaos and the inverse abrupt chaos also occur on each side of the period-3 window, 1/ L ∈ [7.69, 7.74].

Fig. 5. Chaotic attractors of memcapacitor-based oscillator: (a) u c – i L trajectory, (b) q m – u c trajectory, (c) q m – i L trajectory, (d) u cm – q m trajectory.
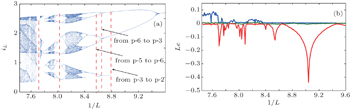Fig. 6. Dynamical characteristics of memcapacitor-based oscillator: (a) bifurcation plot of current i L versus inductance L , (b) Lyapunov exponents versus inductance L .

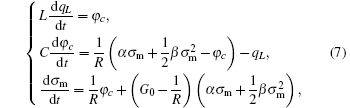
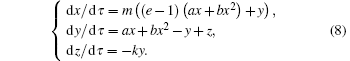
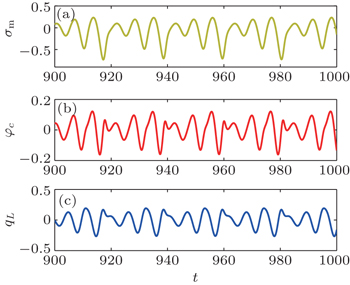
By integrating Eq. ( 5 ) directly with respect to time t and inserting Eq. ( 4 ) into the integrated equations, the following three-dimensional equations with variables q L , φ c , and σ m can be obtained:

where q L = ∫ i L ( t ) d t , φ c = ∫u c ( t ) d t , and σ m = ∫ q m ( t ) d t . Let τ = t / RC , x = σ m , y = φ c , z = − Rq L , m = C , e = RG 0 , a = α , b = β /2, and k = R 2 C / L , equation ( 7 ) can be transformed into the concise form

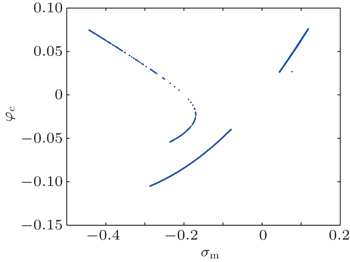
This system has a chaotic attractor with Lyapunov exponents Le 1 = 0.114, Le 2 = 0, and Le 3 = −2.2878 when m = 4.5, e = 0.48, a = 0.7, b = 0.4, and k = 1.75. The trajectories of the circuit variables are shown in Figs. 7(a) – 7(c) ; the σ – φ characteristic curve and the waveforms of σ m ( x ), φ c ( y ), and q L (− z / R ) are shown in Figs. 7(d) and 8 , respectively.

Fig. 7. The (a) φ c − σ m trajectory, (b) q L – φ c trajectory, (c) q L – σ m trajectory, (d) φ m – σ m trajectory.
Fig. 8. Waveforms of (a) σ m , (b) φ c , and (c) q L .
3.2. Basic dynamical characteristics
3.2.1. Dissipativeness and stableness

The divergence of system ( 8 ) is described as

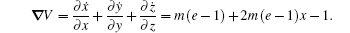
When ∇ V < 0, i.e., x < 1/ m ( e − 1) − 1 or σ m < 1/ C ( RG 0 − 1) − 1, this system is dissipative, hence implying a possible attractor with the convergence rate d V /d t = e −3.34 − 7.488 x , where m = 4.5 and e = 0.48.

Let ẋ = ẏ = ż = 0, we obtain two equilibria, S 1 (0, 0, 0) and S 2 (− a/b , 0, 0). This is different from most memristor-based oscillators, which possess an infinite number of equilibria, or an equilibrium set, or a line equilibrium.

The Jacobian matrix of Eq. ( 8 ) is given by

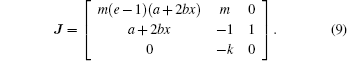
The characteristic equation for the equilibria can be written as

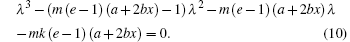
Solving this characteristic equation with the above given parameters, we obtain the characteristic values λ 1 = −2.8973 and λ 2,3 = 0.1297 ± 0.9862i for equilibrium S 1 , and λ 1 = 0.8363 and λ 2,3 = −0.0991 ± 1.8488i for equilibrium S 2 , displaying that both of them are unstable saddle-focus.

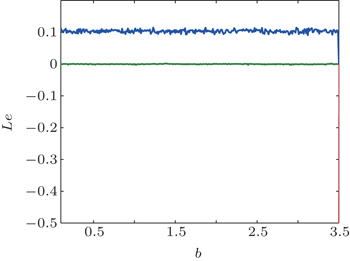
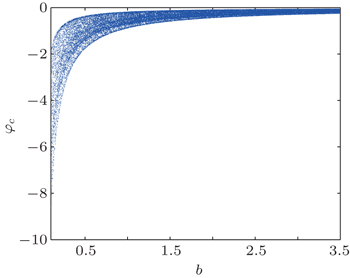
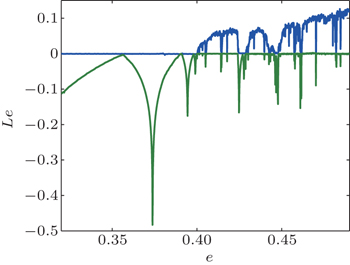
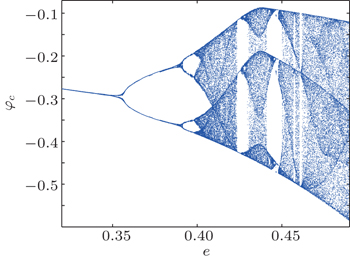
3.2.2. Sustained chaos with constant Lyapunov exponents

The Lyapunov exponent spectrum versus parameter b (for clarity, only the two larger Lyapunov exponents are drawn, similarly hereinafter) and the corresponding bifurcation diagrams are shown in Figs. 9 and 10 , respectively, where m = 4.5, e = 0.48, a = 0.7, k = 1.75, and b ∈ [0.1, 3.5]. From Fig. 9 , we find that the largest Lyapunov exponent is always positive and is approximately constant in the region b ∈ [0.1, 3.5], implying that this system has good robustness with different mamcapacitors and different parameters, and can generate good PN sequences with a big key space.

Fig. 9. Lyapunov exponents versus memcapacitor parameter b .
Fig. 10. Bifurcation of flux φ c through capacitor C versus parameter b .
3.2.3. Abrupt chaos and complex period bifurcations

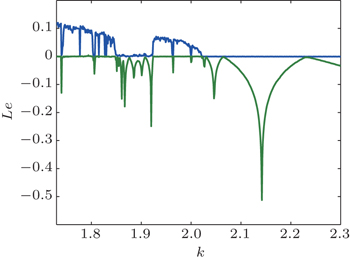
The Lyapunov exponent spectrum and the corresponding bifurcation diagram of variable y versus parameter k are shown in Figs. 11 and 12 , respectively, where m = 4.5, e = 0.48, a = 0.7, b = 0.4, and k ∈ [1.73, 2.3]. Obviously, system ( 8 ) has no solution at k < 1.73, but it is suddenly chaotic without bifurcation at k = 1.73. When k ∈ [1.83,1.92], a novel bifurcation occurs from chaos to period-3 → period-6 → period-3 → chaos; while when k ∈ [1.92,2.3], this system undergoes an inverse period-doubling bifurcation and finally evolves into a period-1 obit.

Fig. 11. Lyapunov exponents versus parameter k .
Fig. 12. Bifurcation of flux φ c versus parameter k .
3.2.4. Double period-3 windows

Figure 13 shows the Lyapunov exponent spectrum versus parameter e , where m = 4.5, a = 0.7, b = 0.4, and k = 1.75, and figure 14 shows the corresponding bifurcation diagram. From Figs. 13 and 14 , it is clear that this system enters a chaotic region after a process of period-doubling bifurcation. Interestingly, there exist two poeriod-3 windows in the chaotic region, and this rarely occurs in the conventional chaotic systems.

Fig. 13. Lyapunov exponents versus parameter e .
Fig. 14. Bifurcation of flux φ c versus parameter e .
3.2.5. Typical period doubling bifurcations

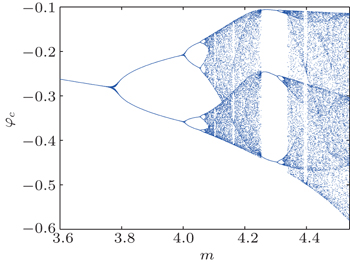
The Lyapunov exponent spectrum versus parameter m and the corresponding bifurcation diagram are shown in Figs. 15 and 16 , respectively, where e = 0.48, a = 0.7, b = 0.4, k = 1.75, and m ∈ [3.6,4.54]. With the variation of capacitance C of the linear capacitor, the memcapactor oscillator exhibits the typical period doubling bifurcation and a period-3 window.

Fig. 15. Lyapunov exponents versus parameter m .
Fig. 16. Bifurcation of flux φ c versus parameter m .
3.2.6. Dynamical map and Poincare section

Now we present the dynamical map of system ( 8 ) in order to simultaneously show the bifurcations of σ m with respect to parameters m (i.e., C ) and e (i.e., R ). It is shown in Fig. 17 , in which the blue region with the label C denotes the chaotic state of the oscillator, while the yellow region with the label P denotes the periodic state of the oscillator. Figure 18 shows the Poincare section for the proposed system, here z = 0.

Fig. 17. Dynamical map with parameters m and e .
Fig. 18. Poincare section for φ c = 0.
4. Analog and digital realizations of the memcapacitor oscillator
4.1. Analog realization

In this section, we give two analog circuit schemes for realizing the proposed memcapacitor oscillator based on the u – q characteristic and the φ – σ characteristic of the memcapacitor, respectively.

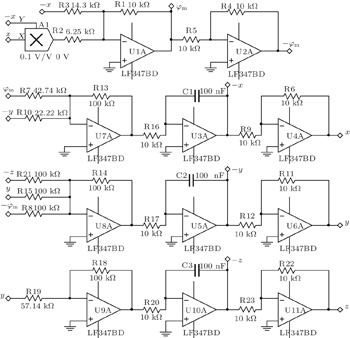
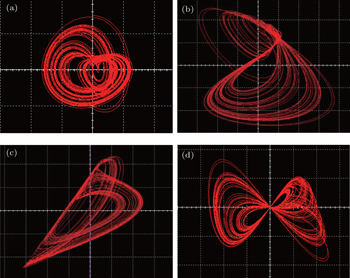The memcapacitor oscillator circuit, which is designed according to the u – q model (i.e., Eq. ( 3 ) and Fig. 2(a) ) and system ( 6 ), is shown in Fig. 19 , and the results of simulation using the Multisim software are shown in Fig. 20 .

Fig. 19. Memcapacitor oscillator based on the u – q circuit model.
Fig. 20. Simulated experimental results: (a) i L – u c phase diagram, (b) u c – q m phase diagram, (c) i L – q m phase diagram, (d) q m – u cm phase diagram.

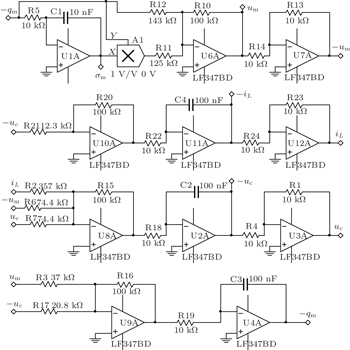
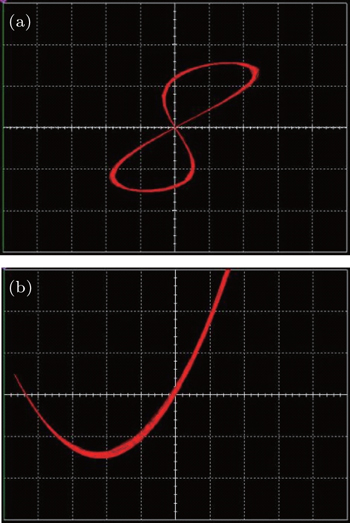
On the other hand, the memcapacitor oscillator circuit designed according to the φ – σ characteristic (i.e., Eq. ( 4 ) and Fig. 2(b) ) and system ( 8 ), is shown in Fig. 21 . The phase portraits of the chaotic signal observed using an analog oscilloscope is shown in Fig. 22 , and the experimental setup is shown in Fig. 23 .

Fig. 21. Memcapacitor oscillator based on the φ – σ circuit model.
Fig. 22. Experimental results of memcapacitor-based oscillator: (a) σ m – φ c phase diagram, (b) φ c – q L phase diagram, (c) σ m – q L phase diagram, (d) σ m – φ m phase diagram.
Fig. 23. Experimental circuit board for memcapacitor-based oscillator.

The significance of the experiment with these charge-controlled memcapacitor circuits is that those circuit variables which are originally observed and measured with difficulties, such as flux φ c in the linear capacitor, flux φ m in the memcapacitor, charge q L on the inductor, and σ m , are directly observed and measured in this experiment. Particularly, the σ m – φ m characteristic described by 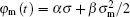is also obtained from the experimental oscilloscope.

4.2. Digital analog realization

Now, we provide a scheme for digitally realizing the proposed charge-controlled memcapacitor oscillator. The reasons for digitally realizing this system are shown as follows. Firstly, the analog chaotic circuit and its synchronization are easily affected by the precisions of the circuit elements and matching of the circuit parameters. Secondly, the digital technology is the mainstream technology for the expected future applications of the memcapacitor oscillation. Thirdly, it is digitalized so that we can detect the random properties of pseudo random sequences generated from this oscillator.

The digital signal processing (DSP) technology is used to realize the charge-controlled memcapacitor system, since the DSP technology is the mainstream technique for digital signal processing at present. Furthermore, the system utilizing the DSP technology is more effective for the practical applications of both pseudo random sequence generation and chaotic information encryption/decryption processing. For this purpose, the iterative form of Eq. 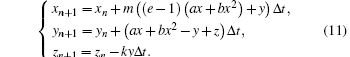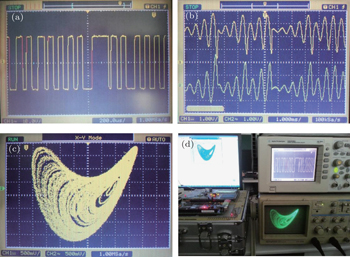( 8 ) is given by applying Euler’s method

Utilizing the DSP evaluation board (ICETEK-VC5509-AE) and the software environment platform CCStudio-v3.3, we can solve Eq. ( 11 ) or ( 8 ) and obtain the variables x , y , and z .

A simple way to generate a binary sequence from the above solved chaotic real value signal is to use the following threshold function:

where x i denotes the value of the i -th decimal place in variable x (or y or z ), i = 5, 6, 7, 8; and c is a constant taking the values of 0, 1, 2, 3, …, 9. Using Eqs. ( 11 ) and ( 12 ), we can obtain digital chaotic sequences which are referred to as binary PN sequences. An experimental binary PN sequence obtained by the DSP evaluation board is shown in Fig. 24(a) . Figure 24(b) shows the waveforms of x and y , which are obtained by a D/A converter. Figure 24(c) shows the phase diagram of x and y , and figure 24(d) shows the experimental setup.

Fig. 24. Digital circuit experiment: (a) chaotic PN sequence digitalized from x , (b) waveforms of x and y , (c) chaotic phase diagram of x and y , (d) experimental setup.
4.3. Statistical tests for randomness of the memcapacitor oscillator

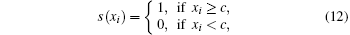
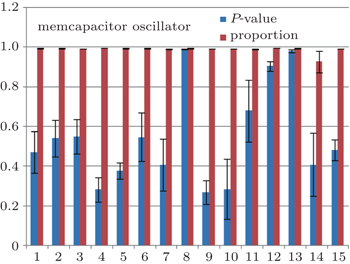
In this section, by using the NIST test suite, the randomness of the proposed memcapacitor oscillator is verified by testing its binary sequences.

The NIST test suite, the most authoritative tool for pseudo-random testing currently, is a statistical software package consisting of 15 tests, which is developed to test the 757 randomness of binary sequences produced by pseudorandom signal generators. The 2.0 version of the test suite package is used in the experiment.

For a binary sequence of ‘0’ and ‘1’ of a given length n , the sequence is divided into k non overlapping parts with equal length m ( k = n/m ), here n = 1000000000 and m = 1000, so k = 1000000.

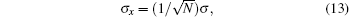
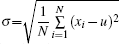
A final analysis report is generated for each test from the test suite package with relevant intermediate values, including test statistics (proportions) and P -values for each test. In order to compare with the well-known Lorenz system, a conclusion describing the quality of the sequences can be obtained by four tests based on these P -values and proportions, shown in Tables 1 and 2 for the memcapacitor oscillator and the Lorenz oscillator, respectively. For ease of comparison between the values of mean and standard error, the data for each level of the standard error are also given in the tables. In Tables 1 and 2 , the standard errors are calculated by

where and N = 4.

Table 1.

Test report of the memcapacitor oscillator.

.
Table 2.

Test report of the Lorenz oscillator.

.

The distribution of P -values is used to examine uniformity. A P -value is calculated from

where

in which F i denotes the number of P -values in sub–interval i , and refers to the sample size.

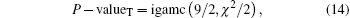
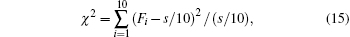
If P − value T ≥ 0.0001, the sequences can be considered to be uniformly distributed. From Table 1 , all statistical test P -values of the memcapacitor satisfy the requirement.

If a value of proportion falls outside the interval defined by 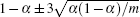, where α is the significance level, then there is evidence that the data are non-random. In the test, α = 0.01, m = 1000, and the confidence interval is (0.98056, 0.99944). From Table 1 , we can see that all statistical test proportions of the memcapacitor fall into the confidence interval.

From Tables 1 and 2 , we can now conclude that the stochastic performance of the memcapacitor oscillator is comparable to the stochastic performance. And most of the tested proportions of the memcapacitor oscillator are better than those of the Lorenz system, such as frequency, block frequency, runs, longest run, rank, non overlapping template, universal, random excursions, random excursions variant, and linear complexity. The corresponding error bars are shown in Figs. 25 and 26 for the proposed memcapacitor oscillator and the Lorenz oscillator, respectively, in which the horizontal axis represents the test item marked with 1, 2, 3, …, 15 in Tables 1 and 2 .

Fig. 25. Sequence of the memcapacitor oscillator.
Fig. 26. Sequence of the Lorenz oscillator.
5. Conclusion

We design a mathematical model of the charge-controlled memcapacitor and its equivalent circuit for future advance studies of memcapacitor. On the basis of this model, a memcapacitor-based oscillator circuit is designed and realized. Theory analysis and experiments show that this oscillator possesses complex dynamical characteristics, such as sustained chaos with constant Lyapunov exponents, burst chaos, and novel irregular bifurcations. Moreover, a digital realization of the oscillator is given by using the DSP technology and the chaotic PN sequence is obtained. Random properties of the PN sequence fully meet the NIST standard, and therefore the proposed memcapacitor oscillator can be used for designing PN sequence generators as a new random signal seed.

Reference
1 Chua L O 1971 IEEE Trans. Circuit Theory 18 507
2 Strukov D B Snider G S Stewart D R Williams R S 2008 Nature 453 80
3 Di Ventra M Pershin Y V Chua L O 2009 Proc. IEEE 97 1717
4 Hu S G Liu Y Chen T P Liu Z Yu Q Deng L J Yin Y Hosaka S 2013 Appl. Phys. Lett. 103 133701
5 Hamdioui S Taouil M Haron N Z 2013 IEEE Trans. Computers 64 247
6 Yu Z Y Tian H Chen G H Chua L O 2015 IEEE Trans. Circuits Syst. II 62 402
7 Kim Y Park K H Chung T H Bark H J Yi J Y Choi W C Kim E K Lee J W Lee J Y 2001 Appl. Phys. Lett. 78 934
8 Lee P F Lu X B Dai J Y Chan H L W Jelenkovic E Tong K Y 2006 Nanotechnology 17 1202
9 Driscoll T Kim H T Chae B G Kim B J Lee Y W Jokerst N M Palit S Smith D R Ventra M D Basov D N 2009 Science 325 1518
10 Lai Q Zhang L Li Z Stickle W F Williams R S Chen Y 2009 Appl. Phys. Lett. 95 213503
11 Krems M Pershin Y V Di Ventra M 2010 Nano Lett. 10 2674
12 Martinez-Rincon J Di Ventra M Pershin Y V 2010 Phys. Rev. B 81 195430
13 Martinez-Rincon J Pershin Y V IEEE Trans. Electron Devices 58 1809
14 Yang F Y Leng J L Li Q D 2014 Acta Phys. Sin. 63 080502 (in Chinese)
15 Li Z J Zeng Y C Li Z B 2014 Acta Phys. Sin. 63 010502 (in Chinese)
16 Bao B C Hu F W Liu Z Xu J P 2014 Chin. Phys. B 23 070503
17 Yu Q Bao B C Hu F W Xu Q Chen M Wang J 2014 Acta Phys. Sin. 63 240505 (in Chinese)
18 Xu B R 2013 Acta Phys. Sin. 62 190506 (in Chinese)
19 Wang G Y He J L Yuan F Peng C J 2013 Chin. Phys. Lett. 30 110506
20 Buscarino A Fortuna L Frasca M Gambuzza L V 2012 Chaos 22 023136
21 Yu D S Liang Y Chen H Herbert H C Iu 2013 IEEE Trans. Circuits Syst. II 60 207
22 Hu Z Li Y Jia L Yu J 2010 International Conference Communications, Circuits and Systems (ICCCAS 2010) July 28–30, 2010 Chengdu, China 828 10.1109/ICCCAS.2010.5581864
23 Hu Z Li Y Jia L Yu J 2010 International Conference Communications, Circuits and Systems (ICCCAS 2010) July 28–30, 2010 Chengdu, China 824 10.1109/ICCCAS.2010.5581863
24 Fitch A L Iu H H C Yu D S 2014 Circuits and Systems (ISCAS), 2014 IEEE International Symposium on June 1–5, 2014 Melbourne, Australia 482 10.1109/ISCAS.2014.6865177
25 Biolek D Biolek Z Biolkova V 2010 Electron. Lett. 46 520
26 Fouda M E Radwan A G 2012 Electron. Lett. 48 1454
27 Wang X Y Fitch A L Iu H H C Qi W G 2012 Phys. Lett. A 376 394