Cite this Article
Hou Wei, Yan Peng-Cheng, Li Shu-Ping, Tu Gang, Hu Jing-Guo. Application of long-range correlation and multi-fractal analysis for the depiction of drought risk. Chinese Physics B , 2016, 25(1): 019201  
Permissions
Application of long-range correlation and multi-fractal analysis for the depiction of drought risk
Hou Wei 1, †, , Yan Peng-Cheng 2 , Li Shu-Ping 2 , Tu Gang 3 , Hu Jing-Guo 4
National Climate Center, Beijing 100081, China
College of Atmospheric Sciences, Lanzhou University, Lanzhou 730000, China
Jilin Meteorological Science Institute, Changchun 130062, China
Department of Physics Yangzhou University, Yangzhou 225002, China

 

† Corresponding author. E-mail: houwei@cma.gov.cn

Project supported by the National Basic Research Program of China (Grant No. 2012CB955901), the National Natural Science Foundation of China (Grant Nos. 41305056, 41175084, and 41375069), and the Special Scientific Research Fund of Meteorological Public Welfare Profession of China (Grant No. GYHY201506001).

Abstract
Abstract

By using the multi-fractal detrended fluctuation analysis method, we analyze the nonlinear property of drought in southwestern China. The results indicate that the occurrence of drought in southwestern China is multi-fractal and long-range correlated, and these properties are indifferent to timescales. A power-law decay distribution well describes the return interval of drought events and the auto-correlation. Furthermore, a drought risk exponent based on the multi-fractal property and the long-range correlation is presented. This risk exponent can give useful information about whether the drought may or may not occur in future, and provide a guidance function for preventing disasters and reducing damage.

PACS : 92.70.Aa
Keyword : multi-fractal detrended fluctuation analysis ; return intervals ; drought risk
1. Introduction

Drought is one of the most severe disasters occurring in China in terms of disaster area and loss. Against the background of global warming, drought in China has become more and more severe in recent years. Particularly in the southwestern China, [ 1 – 3 ] for five successive years (2009–2013), continuous winter-to-spring drought occurred in this region. [ 4 – 7 ] A particularly severe drought event occurred between 2009 and 2010, the drought continued from autumn to winter and then to spring. This was the most severe drought event ever recorded since the recording of meteorological data began, and it resulted in significant economic loss. Much current research focusses on the drought events in southwestern China from the aspects of the cause of drought, [ 4 – 7 ] wet/dry classification, [ 8 , 9 ] social and economic effects, [ 10 , 11 ] etc. The aim of this paper is to study whether the change of drought events can be determined from the analysis of the time series of drought index, so as to extract more effective information to advance the research about drought monitoring and drought early warning. While studying multi-fractal data, Bogachev et al . [ 12 – 14 ] found that if a time series is multi-fractal, then the return interval sequence of the extreme event in this time series has the same auto-correlation exponent as the one of the original time series, and this characteristic will result in the group occurrence of extreme events. [ 15 – 18 ] Consequently, the return intervals of the extreme events obey a decaying power-law distribution. This characteristic has been applied in predicting the occurrence of extreme events in economic time series. [ 15 , 16 ] In consideration of the fact that a drought event can be regarded as a type of extreme event with little precipitation, [ 13 , 19 ] we try to introduce this idea into drought research.

This study adopts the detrended fluctuation analysis method to study the standardized precipitation index (SPI) [ 20 ] time series in southwestern China. This paper consists of three parts. Firstly, we discuss the multi-fractal characteristic of the SPI time series, and analyze the spatial distribution of the long-range correlations of the SPI time series in southwestern China. Secondly, we analyze the auto-correlation coefficient of the SPI time series and the return interval sequence of the drought event. After that, we obtain the risk exponent of the drought event. Finally, the average value of the obtained risk exponent is used as an indicator to identify the risk of future drought events. We then verify the validity of the risk exponent as an indicator of drought events in southwestern China.

2. Data and methods
2.1. Data

This study uses the SPI which is a drought index introduced and applied in many previous studies. [ 9 , 21 , 22 ] In order to calculate the SPI at different timescales, we use monthly precipitation data from 1961 to 2012. The data were obtained from 303 stations within the southwestern China, including Yunnan, Guizhou, Sichuan, and Chongqing. The locations of the stations are shown in Fig.  1 . The monthly precipitation data were released by the China meteorological administration. The contour maps in this paper are plotted by using the kriging interpolation method. The SPI at the 1-month timescale is labeled SPI1. SPI3 and SPI6 are the SPI at 3-month and 6-month timescales, respectively.

Distribution of stations in Southwest China.

2.2. Methods
2.2.1. Auto-correlation coefficient

The auto-correlation coefficient C ( s ) is calculated by

where N is the length of the time series, s is the lag time, is the standardized variate, and indicates the average value of the sequence. We refer to φ i as uncorrelated if C ( s ) is zero when s is positive. If correlations exist up to a certain s × , then the auto-correlation coefficient will be positive up to s × and disappear at values above s × . In the case of long-range correlations, C ( s ) decays as

2.2.2. Multi-fractal detrended fluctuation analysis

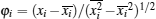
The multi-fractal detrended fluctuation analysis (MFDFA) [ 23 ] is often used in analyzing long-range correlations and multi-fractal properties of a non-stationary time series. [ 24 – 33 ] The algorithm is as follows.

First, calculate the cumulated data series

Divide { Y j } into N s ≡ int ( N / s ) non-overlapping equal-length sub-sequences, each sub-sequence has a length of s . The integral multiple of the sub-sequence length is not exact sometimes, in order to effectively use the residual data after division, a similar division of the sequence is made from the end to the beginning. Then we can obtain sub-sequences and the root mean squared error of each sub-sequence. This is calculated as follows:

in which Y {( k −1) s + j } indicates the sub-sequence, and y k ( j ) is the polynomial fitting of the sub-sequence. We then calculate the average value of the root mean squared error of all sub-sequences to obtain the q -order fluctuation function

In general, the fluctuation function F q ( s ) is a function of the sub-sequence length, F q ( s ) ∼ s h ( q ) , in which h ( q ) is called the Hurst exponent, and is usually obtained by calculating the log–log of F q ( s ) and s . When q = 2, the MFDFA is the same as the detrended fluctuation analysis (DFA). [ 34 ] For the moment, h (2) = H is called the generalized Hurst exponent. The h ( q )is the scaling exponent used for evaluating whether or not the sequence is long-range correlated. When the sequence is single fractal, the deviation has consistent scaling behaviors in all sub-sequences, and h ( q ) is a constant independent of q . It is particularly necessary to point out that h ( q ) = 1/2 when the sequence is uncorrelated or short-range correlated. The sequence is multi-fractal when h ( q ) depends on q and is a function of q . We have

where C is a correlation measurement, [ 35 , 36 ] and H is the Hurst exponent. When H = 0.5, C = 0; it shows non-correlation, namely, the sequence is an independent random white noise, and the past state of the sequence has no influence on the future. When 0 < H < 0.5, C < 0; it shows a negative correlation, namely, the sequence has an anti-persistence property similar to that of pink noise, [ 35 , 36 ] which implies that two adjacent events have an inverse correlation. If the sequence is positive at the previous moment, then it is highly possible that the sequence will be negative at the next moment. When 0.5 < H ≤ 1, C > 0; it shows a positive correlation, namely, the sequence has a persistence characteristic similar to black noise, [ 35 , 36 ] which implies that two adjacent events have a positive correlation. If the sequence is positive at the previous moment, then it is highly possible that the sequence will be positive in the next moment. When H is closer to 0.5, the noise contained in the sequence is larger, the tendency of the sequence is more uncertain.

In general, if a sequence is multi-fractal, then its Hurst exponent h ( q ) has the following relationship with the exponent τ ( q ):

We use the Legendre transformation in Eq. ( 7 ) to obtain a relationship between h ( q ) and the singular spectrum

in which f ( α )∼ α is a multiple-fractal singularity spectrum, [ 19 , 26 ] and the spectral width, the maximum value f max ( α ), and the asymmetry of the spectrum are the three characteristic quantities of the multiple fractals. These three characteristic quantities are typically used to describe the multiple-fractal degree. The larger the spectrum width, the larger the f max ( α ). The more obvious the asymmetry of the spectrum, the more obvious the multiple fractal characteristics. [ 26 ]

2.2.3. Return intervals of drought events

The drought grade of SPI is usually defined according to the probability distribution, and it will usually be in a drought state when the SPI is smaller than 0. [ 20 ] For an SPI time series, the corresponding drought event sequence can be established by a given threshold Q . The time interval of two adjacent drought events is defined as the return interval of drought events r i ( i = 1,2,3, …, N ), as shown in Fig.  2 . For the convenience of analysis, [ 20 ] Q = −0.5 is taken as the threshold value in this paper, i.e., the drought events of light grade and above are studied.

Return intevals of drought.

3. Analysis of the drought exponent
3.1. Multi-fractal analysis

As an example, the analysis of the SPI1 time series of Chuxiong based on MFDFA is performed, and the results are shown in Fig.  3 . Figure  3(a) is a bi-logarithmic diagram that shows the change of q -order fluctuation function F q ( s ) with the length of sub-sequence, s . It can be seen from the figure that the fluctuation function F q ( s ) scales with s as F q ( s )∼ s h ( q ), and the slope is the Hurst exponent h ( q ). The slopes of various curves with different q are different, which is the multi-fractal characteristic. The relationship between F q ( s ) and s becomes unstable when s is larger than a certain value (the dashed box in Fig.  3(a) ), and becomes sensitive to s . Figure  3(b) shows the non-linear relationship between the scaling exponent τ ( q ) and q , in which the scope of q is [−10, 10] and the length of interval is 2. This also explains the multi-fractal property of the SPI1 sequence. In order to understand the relationship between h ( q ) and q more intuitively, the relationship between them is presented in Fig.  3(c) , in which the horizontal dashed line is the threshold value used to determine the long-range correlation of the SPI1 sequence; and the vertical dashed line refers to the Hurst exponent. It can be seen that h ( q ) is not fixed, but rather a function of q , which means that each sub-sequence has a different scale and further demonstrates the multi-fractal property of the SPI1. It can also be seen from Fig.  3(c) that when − 10 ≤ q < 6, 0.5 < h ( q ) < 1. This shows that the SPI1 sequence has a positive correlation, i.e., persistence property. Furthermore, when 6 < q < 10, 0 < h ( q ) < 0.5; it shows that the SPI1 sequence has an inverse correlation, i.e., anti-persistence property. The multi-fractal spectrum obtained from Eq. ( 8 ) is presented in Fig.  3(d) . The spectrum width is 0.26 and the maximum value is 1.0, which reflects the multifractal characteristic of the SPI1 sequence in a better way. The curve in Fig.  3(d) has a left hook shape. After the analysis of the data from the 303 stations, it is found that if the Hurst exponent is larger than 0.5, then the multi-fractal spectrum has a left hook shape. On the contrary, if the Hurst exponent is smaller than 0.5, then the multi-fractal spectrum has a right hook shape. Moreover, the change of |Δ f | is consistent with the change of | h (2) − 0.5|, and Δ f = f ( α min ) − f ( α max ).

The multi-fractal measures of Chuxiong: (a) q -order wave function F q ( s ), (b) quality index τ ( q ), (c) the generalized Hurst index h ( q ), and (d) the multi-fractal spectrum f ( d )∼ d .

Multi-fractal analyses are completed by using the MFDFA method. The analysis results of the SPI sequences with different timescales from other stations are very similar to the analysis results of the SPI1 sequence at Chuxiong. It can be seen from the results that the SPI sequence with different timescale at each station in southwestern China has multifractal characteristics. In addition, the multi-fractal scale exponent (Hurst exponent) obtained via the MFDFA method is sensitive to the length of sub-sequence, s . When s is larger than a certain value, the Hurst exponent shows instability. In summary, the SPI in southwestern China is multi-fractal.

3.2. Long-range correlation analysis

In general, the Hurst exponent ( q = 2) is used as the scale exponent to examine the correlation characteristic of a time series. Figure  4 shows the spatial distributions of the Hurst exponent h (2) in southwestern China for three timescales (SPI1 of Fig.  4(a) , SPI3 of Fig.  4(b) , and SPI6 of Fig.  4(c) ). Two representative stations are selected (Fig.  4(d) ) according to whether or not the Hurst exponent is larger than 0.5. For SPI1, the spatial distribution of the Hurst exponent shows a declining trend from the southwest to the northeast. The Hurst exponent in the west (except for western Yunnan province) is larger than 0.5 and shows a positive correlation. The Hurst exponents in other regions are smaller than 0.5 and show a negative correlation.

Figure  4(d) shows two representative stations where the SPI1 sequences have different long-range correlation characteristics. The Hurst exponent of Chongqing (triangle) is smaller than 0.5, i.e., the SPI1 sequence shows a negative correlation. The Hurst exponent of Bijie (circle) is larger than 0.5, i.e., the SPI1 sequence shows a positive correlation. The results for SPI1, SPI3, and SPI6 are similar.

The spatial distributions of the Hurst index for different time scales in southwestern China: (a) SPI1, (b) SPI3, and (c) SPI6, (d) SPI1 with two stations marketed, one with a Hurst index less than 0.5 (triangle), and one with a Hurst index greater than 0.5 (circle).

4. Return interval sequence analysis

The characteristics of the drought index series are also shown in the return interval sequence of drought events, and the probability density distribution and the auto-correlation coefficient of the return interval sequence obey a power-law distribution. [ 15 , 31 ] Therefore, if the size of a sequence is insufficient, then the long-range correlation of the sequence can be determined in this way. We first analyze the SPI1 sequence and then examine the return interval sequence of drought events. The sample size is limited due to the length of the return interval sequence of the drought event, thus the MFDFA method cannot be used to analyze the long-range correlation directly. [ 32 ] Therefore, we calculate the probability density distribution and the auto-correlation coefficient of the return interval sequence, as shown in Fig.  5 .

Log–log plots of the probability densities of return intervals of (a) Chongqing, (b) Bijie; and log–log plots of the autocorrelation coefficients of (c) Chongqing, (d) Bijie.

Figures  5(a) and 5(b) show the probability density distributions of the return interval sequence of drought events at Chongqing and Bijie, respectively. Figures  5(c) and 5(d) are the bi-logarithmic diagrams of the auto-correlation coefficients of the return interval sequence of the drought events at the two stations, in which −0.5 is taken as the threshold value Q . It can be seen from Figs.  5(a) and 5(b) that the probability density distributions of the return interval sequence of drought events at the two stations follow a power-law relationship

where r i is the return interval sequence, P Q ( r ) is the probability density distribution of the return interval sequence, and is the average return interval. Similarly, the auto-correlation coefficients of the return interval sequence of drought events at the two stations have a decaying power-law distribution, and the power-law relationship is

where C Q ( s ) is the auto-correlation coefficient, and s is the lag time. For a sequence which is multi-fractal (either positive or inverse correlation), the probability density distribution of the return interval sequence of extreme events in the sequence has a decaying power-law distribution. Furthermore, its autocorrelation coefficient has a decaying power-law distribution. So, the return interval sequence of the SPI1 time series also shows a long-range correlation.

5. Drought risk exponent
5.1. The algorithm of drought risk exponent

As the return interval sequence of drought events, as shown in Eq. ( 10 ), has a long-range correlation, i.e., there is a certain relationship between two successive drought events and this relationship may be used as a precursory indicator of the drought events in future, a model for evaluating the risk of drought events can be established. [ 12 – 14 ] To accurately establish the model, the sequence in question must have a longrange correlation and a multi-fractal nature. This will guarantee that the return interval sequence of drought events will have similar characteristics. This model can only be used when the return interval sequence has a long-range correlation.

The probability density function of return intervals of Chongqing.

Figure  6 shows the probability density distribution of the return interval sequence of the drought events at Chongqing, in which the horizontal coordinate r / R Q is the ratio between the return interval and the average return interval, the vertical coordinate is the probability. As can be seen, probability P Q shows a decaying power-law characteristic. If we assume that the time interval between the current time and the ending time of the previous drought event is x (as shown in Fig.  6 ), the left part of the dashed line of x may not be considered. This is because the time interval between the future drought event and the previous drought event cannot be smaller than x . Therefore, the risk of drought event at a certain time in future is defined as the ratio between the probability of drought event at that certain time and the probability of drought at all time after current time, namely,

where W Q ( x ,Δ x ) is the risk exponent defined in this paper, and it is the possibility of drought events within a certain period in the future. Here P Q ( r ) is the probability density of the return interval sequence, Q is the threshold value of drought, x is the time interval from the current time to the ending time of the previous drought event, and Δ x is the length of a certain period in the future to be considered and signifies that the drought event will occur within the period of x + Δ x . The value of Δ x can be changed according to specific demands. By taking the SPI1 sequences of Chongqing and Bijie between 1980 and 2012, we provide the risk exponent W Q ( x ,Δ x ), as shown in Fig.  7 .

The SPI1 index sequences of (a1) Chongqing, (b1) Bijie, and the risk indexes of drought of (a2) Chongqing, (b2) Bijie.

Figure  7 shows the SPI1 sequences and the risk exponents of Chongqing and Bijie. The Δ x here is taken as 1, i.e., the risk of drought events within one month in the future. Figures  7(a1) and 7(a2) show the results for Chongqing; and figures  7(b1) and 7(b2) show the results for Bijie. It can be seen from these figures that the SPI1 and the frequency of drought events are smaller at Chongqing, and the risk exponent is also smaller (Fig.  7(a2) ). The SPI1 and the frequency of drought event are larger at Bijie, and the risk exponent value is larger too (Fig.  7(b2) ). In addition, the risk exponent can also accurately reflect the risk of stronger or weaker drought events. For example, the SPI1 of Bijie is smaller from 1995 to 2000, and the risk exponent agrees with it, namely, the risk exponent of Bijie is smaller than that of Chongqing.

5.2. The accuracy rate of drought risk exponent

In order to determine the accuracy rate of the risk exponent, we show in Fig.  8 the probability density distribution of the monthly risk exponent at each station in southwestern China, namely, the accuracy rate of this risk exponent. [ 37 ] The calculation equation of this accuracy rate is

where r c is the times that the risk exponent W n in a month exceeds the average value of all risk exponents in 1961–2012 and the SPI1 for the month is smaller than −0.5; r is the times that W n exceeds the average value of all risk exponents in 1961–2012. The accuracy rate of the risk exponent in southwestern China is above 84%, furthermore, the accuracy rate is higher in the north of this area.

The spatial distribution of the accuracy rate of risk index of drought of SPI1 index in southwestern China.

6. Discussion and conclusion

In this study, we analyze the long-range correlation of SPI at each station in southwestern China by using the multifractal method. Based on the characteristic that the return interval sequence of drought events obeys a decaying power-law distribution, we obtain a risk exponent which can be used to determine the probability of a drought event in future. The main conclusions of this study are listed as follows.

The above analysis shows that we can predict the drought event based on the statistics of historical data with a certain degree of accuracy. If combined with the dynamic factor and the water vapor condition of the previous time, it is possible to provide a more accurate result for predicting, monitoring, and warning drought events in China, so as to minimize the economic losses caused by the events.

Reference
1 Huang J P Minnis P Yan H R 2010 Atmos. Chem. Phys. 10 6863
2 Qiu J 2010 Nature 465 142
3 Dai A 2012 Nat. Climate Change 3 52
4 Barriopedro D Gouveia C M Trigo R M Wang L 2012 J. Hydrometeor 13 1251
5 Huang R H Liu Y Wang L Wang L 2012 Chinese Journal of Atmospheric Sciences 36 443 (in Chinese)
6 Duan H Wang S Feng J 2013 Journal of Arid Meteorology 31 633 (in Chinese)
7 Sun J Q 2014 Chin. Sci.Bull. 59 3465
8 Yang J Gong D Wang W Hu M Mao R 2012 Meteorol. Atmos. Phys. 115 173
9 Chen H P Sun J Q Chen X L 2013 Atmos. Oceanic Sci. Lett. 6 5
10 Wang L Chen W Zhou W 2014 Adv. Atmos. Sci. 31 1035
11 Wang W Wang W J Li J S Wu H Xu C Liu T 2010 Procedia Environ. Sci. 2 1679
12 Boagchev M I Eichner J F Bunde A 2007 Phys. Rev. Lett. 99 240601
13 Boagchev M I Bunde A 2008 Phys. Rev. E 78 036114
14 Boagchev M I Bunde A 2009 Phys. Rev. E 80 026131
15 Bunde A Eichner J F Kantelhardt J W Havlin S 2005 Phys. Rev. Lett. 94 048701
16 Eichner J F Kantelhardt J W Bunde A Havlin S 2007 Phys. Rev. E 75 011128
17 Qian Z H Hu J G Cao Y Z 2012 Chin. Phys. B 21 109203
18 Zhao J H Wang Q G Zhi R Feng G L 2012 Acta Meteorologica Sinica 70 302
19 Kantelhardt J W Bunde E K Rybski D Braun P Bunde A Havlin S 2006 J. Geophys. Res. 111 D01106
20 McKee T B Doesken N J Kleist J 1993 Eighth Conf. on Applied Climatology, Anaheim, CA, Amer. Meteor. Soc. 179 184
21 Gao H Yang S 2009 J. Geophys. Res. 114 D24104
22 Orlowsky B Seneviratne S I 2013 Hydrology and Earth System Sciences 17 1765
23 Kantelhardt J W Zschiegner S A Koscielny Bunde E Bunde A Havlin S Stanley H E 2002 Physica A 361 87
24 Hong Y F Li Y H 2012 Fronters of Physics 3 261
25 Lovejoy S Schertzer D 2012 Nonlinear Proc. Geophys. 19 513
26 Norouzzadeh P Rahmani B 2006 Phys. A 367 328
27 Ruan Y P Zhou W X 2011 Phys. A 390 1646
28 Lin M Yan S X Zhao G Wang G 2013 Commun. Theor. Phys. 59 1
29 Kantelhardt J W Bauer A Schumann A Y Barthel P Schneider R Malik M Schmidt G 2007 Chaos 17 015112
30 Sun D Y Zhang H B Huang Q 2014 Acta Phys. Sin. 63 209203 (in Chinese)
31 Wang D L Yu Z G Anh V 2012 Chin. Phys. B 21 80504
32 Zhou Y Leung Y Yu Z G 2011 Chin. Phys. B 20 90507
33 Zhu S M Yu Z G Ahn V 2011 Chin. Phys. B 20 10505
34 Peng C K Buldyrev S V Havlin S 1994 Phys. Rev. E 49 1685
35 Peters E E 2002 Fractal Market Analysis Beijing Economic Science Press 3 36 (in Chinese)
36 Peters E E 1999 Chaos and Order in the Capital Markes translated by Wang X D 2nd Edn. Beijing Economic Science Press 33 150 (in Chinese)
37 Li T 2008 Multifractals: Theory and Some Application Beijing Beijing Jiaotong University 22 29 (in Chinese)