† Corresponding author. E-mail:
The wave function temporal evolution on the one-dimensional (1D) lattice is considered in the tight-binding approximation. The lattice consists of N equal sites and one impurity site (donor). The donor differs from other lattice sites by the on-site electron energy E and the intersite coupling C . The moving wave packet is formed from the wave function initially localized on the donor. The exact solution for the wave packet velocity and the shape is derived at different values E and C . The velocity has the maximal possible group velocity v = 2. The wave packet width grows with time ∼ t 1/3 and its amplitude decreases ∼ t −1/3 . The wave packet reflects multiply from the lattice ends. Analytical expressions for the wave packet front propagation and recurrence are in good agreement with numeric simulations.
Charge transfer (CT) is the key event in many processes in living and inorganic matter; photosynthesis, breathing and many others are the well known examples in living matter. [ 1 – 6 ] Very efficient CT was found later in synthetics analogous of DNA and polypeptides. [ 7 – 11 ] These substances have well organized structures consisting of repeating units, DNA bases (usually adenine) or peptide groups, and represent very good models for CT in one-dimensional systems.
The tight-binding approximation (TBA) is an efficient tool to study the CT. This approach is dated back to the Slater– Koster paper. [ 12 ] The TBA single-particle Hamiltonian can be written as 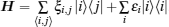
Many efforts were undertaken to study the wave function evolution using the TBA approximation. One well investigated example is the TBA on the disordered lattice. The case of the static disorder, when on-site energies take random values, received special attention. The Anderson localization [ 13 ] was studied extensively employing the TBA Hamiltonian. [ 14 – 18 ]
Two models of random values distribution are studied most often. In the first model, random on-site energies ɛ i are chosen uniformly from the interval [− W /2, W /2], with W denoting the disorder strength. [ 19 , 20 ] Random values in the second model are determined as ɛ i = λ cos(2 πiσ + ϕ ). On-site energies are random values if σ is incommensurate with the lattice period. [ 21 , 22 ]
It has been known that if the disorder strength is moderately small, then the moving wave packets are formed from the initially localized wave function. This moving wave function pulse can transport the charge. In studies of the wave packet dynamics it was found that the wave packet initially moves ballistically ∼ t , but at large times the wave packet movement is diffuse ∼ t β with β taking a wide range of values. [ 23 , 24 ] By virtue of problems associated with the investigations of random lattices, most of the studies were performed by approximate methods or numerically.
In the present paper, we consider the problem of the wave function temporal evolution. The TBA approximation is utilized. The lattice is homogeneous, i.e., both types of disorder–diagonal and off-diagonal, are absent. The wave function is initially localized on one site, i.e., ψ j ( t = 0) = δ j ,1 . The formed moving wave packet can multiply reflect from the ends of the lattice. It should be remembered that the recurrence phenomena to the initial state are in general well known. The Fermi–Pasta–Ulam recurrence is an example of nonlinear classical dynamics. [ 25 , 26 ] The other example is the interaction of the isolated vibrational mode with the continuous spectrum. [ 27 ]
The recurrence in quantum systems was considered by Zwanzig [ 28 ] for the discrete equidistant spectrum where a single level is initially occupied. The analysis of the Zwanzig’s problem was performed for the resonance [ 29 ] and for the non-resonance [ 30 ] cases.
There is a further point to be outlined. The considered TBA model can also govern the evolution of vibrational excitations. The vibrational energy transport in molecular wires was considered by Benserskii and coauthors. [ 31 , 32 ] The recurrence phenomena (Loschmidt echo) in molecular chains and nanoparticles was also analyzed. [ 29 ]
In the present paper we thoroughly analyze the simplest case of the defect-free lattice. Nevertheless the considered model can be relevant to systems with defects if the disorder strength is not too large. It is known for the three-dimensional lattices, that the critical value W , below which the system is conductive, is rather large, W cr ≈ 8.59 ± 0.05. [ 33 ]
It worth mentioning that Anderson’s localization theorem [ 13 ] is, strictly speaking, valid for one-dimensional systems in the thermodynamical limit ( N → ∞). The situation differs for the final-sized systems. There is the scaling which relates the parameters N and W cr . [ 33 – 38 ] But W cr does not depend on N in one-dimensional systems and, according to our preliminary results, lies in the region W cr ≈ 2. It means that if the diagonal disorder strength W ≲ 2 then results obtained for the defect-free lattice can be applicable to systems with defects.
If defects are off-diagonal, e.g., due to thermal fluctuations, then the above mentioned arguments are also valid. The defect-free approximation is fulfilled if the temperature is not too high ( kT /2 in one-dimensional systems should be compared with a critical value W cr ).
Exact expressions are also derived for the wave packet shape and velocity at arbitrary time instants including the wave packet parameters after reflections. This is done for the most interesting case when the wave function is initially totally localized on the lattice end which plays the role of an electron donor in experiments on the charge transfer in DNA. [ 8 , 9 ]
The “electron ping–pong” was found experimentally in DNA, [ 39 ] when a charge is triggered consecutively within the same DNA duplex after a charge injection. This phenomenon is also considered and analytical expressions for the wavefunction amplitude on the electron donor are derived.
The considered problem is relevant to the charge transport and our results mimic to some degree the numerous experiments on charge transfer in low-dimensional systems. Because the wave function evolution is governed by the quantum mechanics laws, the problem under consideration is designated as the quantum dynamics of charge transfer.
We consider the lattice consisting of ( N +1) sites. The left-most site is the “electron donor”. The wave function is initially totally localized on this site. Other N sites are a “reservoir” through which the wave function spreads.
In the second quantization representation, the TBA Hamiltonian is of the form
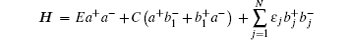

We consider a simple model when all on-site energies of the reservoir are equal and ɛ j = const = 0, which corresponds to the choice of the reference point for the electron energy. All intersite couplings on the lattice ξ j −1, j = 1, which corresponds to the choice of the energy unit. In general, E ≠ 0 and C ≠ 1 for the coupling between the donor and the reservoir.
It is instructive to rewrite the Hamiltonian (


The problem is to find how the electronic populations on all sites change in time. The dimensionless ( ħ = 1) Schrödinger equations for the wave function evolution have the form

If Eq. (
The goal of the present paper is to consider the wave packet spreading through the lattice and its reflections from the lattice ends. The quantum dynamical problem of the wave function evolution can be considered as the interaction of the donor with the reservoir. It is solved using the expansion in terms of the eigenfunctions of the reservoir. The reservoir is represented by the N × N tridiagonal matrix with zero leading diagonal and the unity values on the secondary diagonals (highlighted in bold in Eq. (
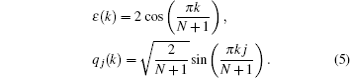
It is convenient to consider the problem in terms of amplitudes of modes b ( k ) instead of amplitudes on the lattice sites b j . These values are related by the orthogonal relationship
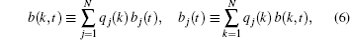
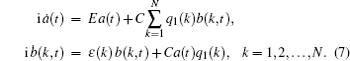
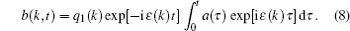
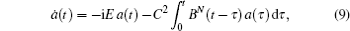
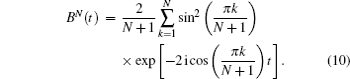
In the next section, we solve Eq. (
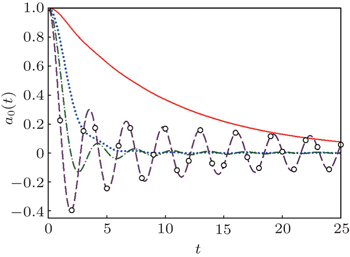
Initially, we consider the decay kinetics of the initial state a ( t = 0) = 1 in the semi-infinite lattice ( N → ∞). The amplitude on the donor is labelled by a 0 ( t ) in this case. The limit N → ∞ for the kernel B N ( t ) is also used. The expression for B N ( t ) is denoted by B 0 ( t ) at N → ∞. In this limit, equation (
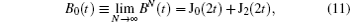

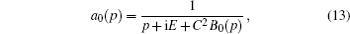
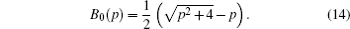

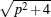
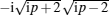
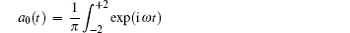
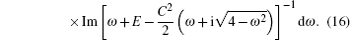
Few special cases can be noted, when the integral (
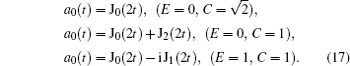
An integro-differential equation for the amplitude a 0 ( t ) is additionally derived in Appendix A, and its solution is obtained as a series of Bessel functions. The series is rather cumbersome, but expressions take simple forms in several particular cases.
Figure
The time dependence of the amplitude a 0 ( t ) for small C can be estimated by the Fermi’s golden rule, when the perturbation approximation in small parameter C 2 is used, and when an exponential decay occurs,
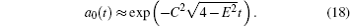
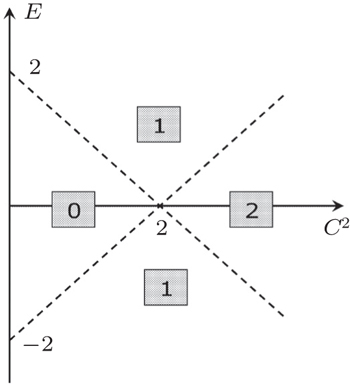
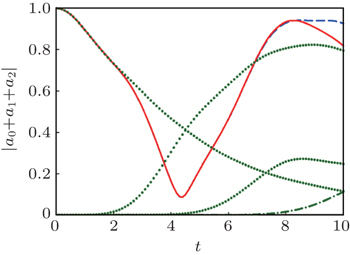
Now the case when the amplitude a 0 ( p ) has poles is considered. An analysis shows that one pole exists in the domain E > 2 − C 2 , and two poles, when E < C 2 − 2. There are no poles in the domain | E | < 2 − C 2 ( C 2 < 2). Figure
As an example, we consider the case of one pole in the domain E > 2 − C 2 ( C 2 < 2). The pole is at the point p = − i ɛ ( ɛ > 2). The relation between parameters E and C follows from Eq. (
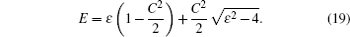
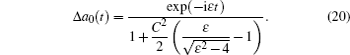
The full amplitude is then the sum of the leading term (
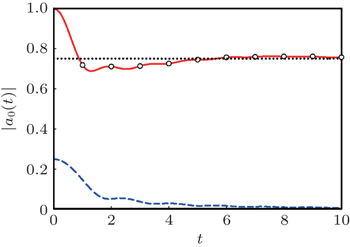
It is shown in Appendix C that if | E | > 2 − C 2 ( C 2 < 2), then there exists the bound state localized at the lattice end on the donor. The value ɛ (see Eq. (
Such a detailed analysis of the amplitude a 0 ( t ) decaying in the semi-infinite lattice is performed due to two reasons. First, the decay kinetics in the semi-infinite lattice coincides with the kinetic in the finite lattice consisting of N sites in the time range 0 ≤ t ≲ N /2. Second, as will be shown below, the full amplitude in the finite lattice can be represented as a sum of partial amplitudes, the first of which is just the amplitude a 0 ( t ) studied above in such detail.
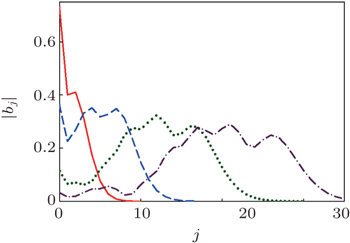
In this section, we will consider the quantum dynamics of the wave function on the lattice, i.e., amplitudes b j ( t ) variation with time. The moving wave packet gradually gains a well formed shape with a sharp leading front. This behavior is shown in Fig.
An expression for amplitudes b j ( t ) is obtained substituting the expression (

Initially, we consider the case of semi-infinite lattice ( N → ∞). Changing the summation in Eq. (

We consider the case when time t is so large that the amplitude a 0 ( t ) becomes very small, | a 0 ( t )| ≪ 1. Then the upper limit in the integration over time in Eq. (
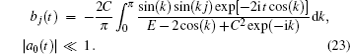
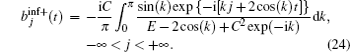
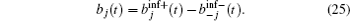
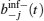

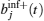
Expression 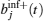
We analyze the expression (

Figure
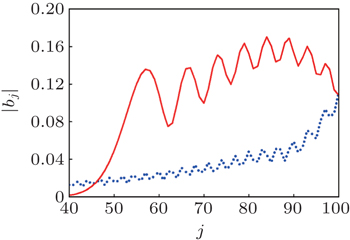
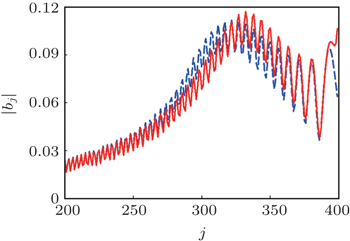 | Fig. 7. The pulse leading edge at t = 200. Dashed line represents the numeric result, solid line represents the asymptotic expansion ( |
If j ≈ 2 t , then both stationary points lie close to k = π /2 and the stationary phase method gives false results (the answer diverges if both points coincide). We consider the region j ≈ 2 t , corresponding to the pulse maximum and its leading edge, in more details. In this case, the expression for amplitudes (
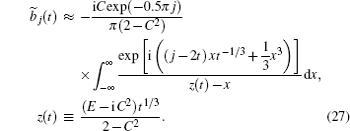
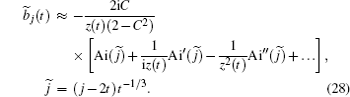
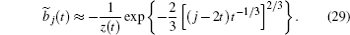
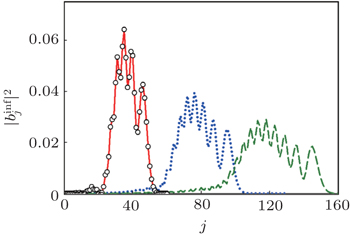
Figure
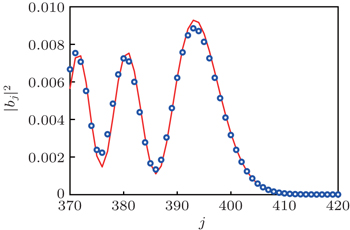 | Fig. 8. The pulse front at t = 200 ( E = 1, C 2 = 2). Empty circles: numeric result, solid line: asymptotic expansion ( |
Expression (
Figure
The pulse width also changes. The wave packet width can be estimated by the radius of the quantum excitation defined in the considered model as
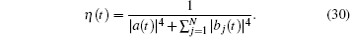
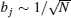
The velocity of the pulse front is 2, maximal possible group velocity. The leading edge has a sharp profile. Thus, if the finite lattice is considered, then until the front achieves the lattice end, its propagation is the same as in the infinite lattice. The pulse front achieves the lattice end at t ≈ N /2. After that the pulse reflects from the lattice end and the front moves backward to the donor.
Afterwards we consider the pulse reflection. We assume that the lattice is long enough. Then the amplitude a ( t ) on the donor is negligible and the pulse is fully formed. The pulse leading edge, moving with the velocity v = 2, reaches the lattice end at t ≈ N /2. After reflection it moves with the same velocity v = 2 in the opposite direction. At t ≈ N the pulse reaches the donor on the left end (see Fig.
To derive an expression for the reflected pulse we return to the expression (
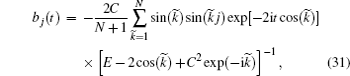
This expression can be transformed using the Poisson summation formula
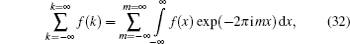
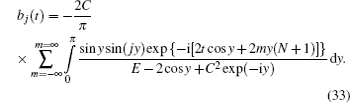

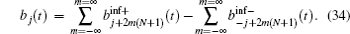
For the separating terms, which are relevant in the considered time domain (1 ≪ t < N ), the expression ( 
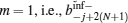
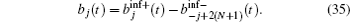
Figure
At the instant t ≈ N the pulse leading edge returns to the lattice beginning and starts to interact with the donor. Amplitude a ( t ) increases. Our approximation concerning the smallness of a ( t ) becomes invalid. The system begins its return to the initial state. This process is analyzed in the next section.
Starting from the initial condition a ( t = 0) = 1 the pulse, having the well formed shape, spreads through the lattice with the velocity v = 2. If the lattice consists of N sites, then the time of the first returning to the donor is t ≈ N . The cycle of k recurrences takes time t ≈ kN . We solve the Eq. (
In order to make sure in this kind of possibility, the kernel B N ( t ) (Eq. (
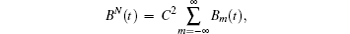
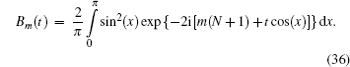
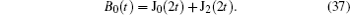
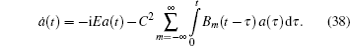
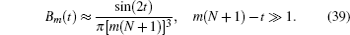
Now we represent amplitude a ( t ) as the sum of partial amplitudes
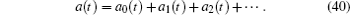
Prior to writing down an equation for a k ( t ), we make one comment. Terms B m ( t ) are small (even for not too long lattices). This smallness is ensured by the fact that B − m ( t ) = B m (− t ), and B m ( t ) ∼ ( mN ) −3 in the considered time range ( t > 0). Nevertheless terms with negative indices m are taken into account as their accounting allows one to derive explicit analytical formulaes.
We introduce functions B̃ m ( t ) to account for the contributions from B m ( t ) ( m < 0)
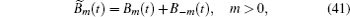
Now in accordance with our assumptions, we convert Eq. (
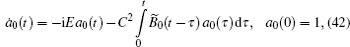
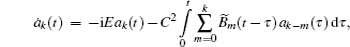

The Laplace transformation of Eq. (
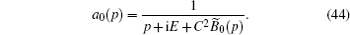
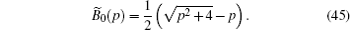
The Laplace transformation of system (


An explicit form of this integral can be obtained. With this aim in view, the integration contour is deformed as shown in Fig.
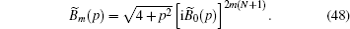
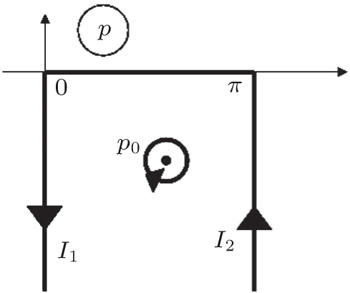 | Fig. 12. The integration along the path [0, π ] in expression ( |
The Laplace transforms of the partial amplitudes a k ( p ) ( k > 0) are expressed as
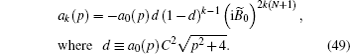
To get explicit expressions for the partial amplitudes, the inverse Laplace transform is made. Transforming the Laplace integral to the integration path around the cut [−2i, 2i], one gets an expression for a 0 ( t )
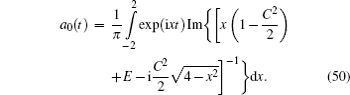
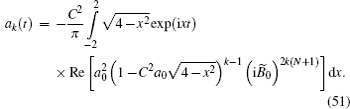
Therefore, if the partial sum a 0 + a 1 + ··· + a k is taken for the representation of amplitude a ( t ), then the error of such approximation is of the same order as the smallness of B̃ k ( t ), i.e., ∼ [( k + 1)( N + 1)] −3 .
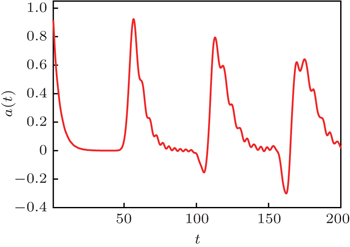
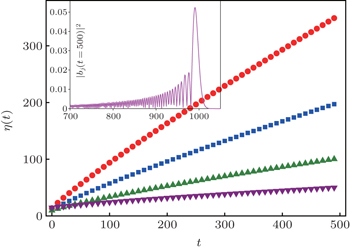
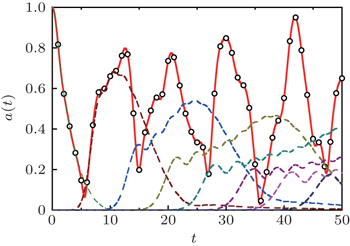
Consider as an example, the most unfavorable case of a very short lattice ( N = 2), and as an approximation, the sum of only three partial amplitudes a 0 + a 1 + a 2 . In Fig.
If the lattice is long enough then partial amplitudes, following each other, have enough time for damping on the corresponding time ranges [ t , t + N ]. In this case partial amplitudes do not interfere and reproduce the total amplitude with very high accuracy (see Fig.
Partial amplitudes interfere on short lattices and maxima of returning amplitudes are irregular. The dependence of the total amplitude a ( t ) versus time for the lattice with N = 10 is shown in Fig.
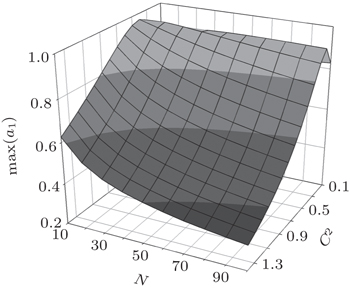
Incident and reflected pulses interfere on short lattices and the degree of returning is difficult to analyze at arbitrary parameter values C , E , N , but the first returning (maximal value of the partial amplitude a 1 ( t )) can be treated analytically if the lattice is long enough when the amplitude a 0 ( t ) becomes negligible.
The expression (
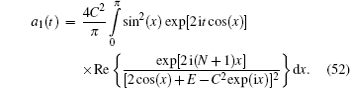
Figure
The wave function pulse, responsible for the charge propagation through the lattice, moves starting from the donor at the lattice end. If the electronic excitation is totally localized on the donor then, depending on the donor parameters, few scenarios of the quantum dynamics are realized. One of the most common cases is the formation of a pulse and its spreading through the lattice. The pulse moves with the maximal group velocity v = 2 and has the steep leading edge. The pulse amplitude decreases ∝ t −1/3 and the width increases ∝ t 1/3 . After reaching the opposite lattice end, the pulse reflects and moves in the opposite direction. This process can repeat many times.
The other scenario is realized if the parameters of the donor are such that the bound state is formed. Then the wave function is partially captured by this bound state. The analytical expressions describing the impulse dynamics coincide with the accurate numeric simulation with high precision.
There are several functions which describe the charge transfer employing the wave packet amplitudes b j ( t ). These include the first: 

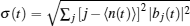
Different dependencies for probabilities and velocities of the pulse spreading are obtained as functions of the models used, and their parameters. Usually the dependence M 2 ( t ) ∝ t β is fulfilled. The power index β falls within the range 0 < β ≤ 2. The ballistic transport ( β = 2) is realized in the considered case of the defect-free lattice. If the lattice has the diagonal or/and off-diagonal disorder, then β < 2 and one or the other diffusion behavior is observed. Unusual hyperdiffusion cases when β > 2 are also known. [ 41 , 42 ] The second moment M 2 ( t ) is mostly calculated numerically, integrating the system similar to Eq. (
The problem of the electronic excitation spreading through the lattice formulated in a rather simple form, can be relevant to recent experiments on the charge transfer in synthetic olygonucleotides, polypeptides, and other non-metallic systems. At one time, it seemed that the polaron mechanism can adequately explain the charge transport in such substances. [ 43 – 50 ]
However, at least two weak points in the polaronic paradigm exist. First, polaron formation. After a charge is transferred to the chain, it should be more or less localized for some time allowing the polaron formation. The characteristic “dynamical” time of the lattice rearrangement 
The second problem is how the polaron can get an initial momentum necessary for the coherent movement. The initially formed unmovable polaron can start to move randomly (one-dimensional random walk) only under the influence of thermal fluctuations. Its diffusive movement cannot explain the experimentally observed single-step coherent transport. [ 9 ] As to our best knowledge, there exists the unique mechanism obeying the movement: When the next-to-nearest-neighbour interactions are included, for physical values of the parameters, polarons can spontaneously move, at T = 0, on bent chains that exhibit a positive gradient in their curvature. [ 51 ]
The discussed mechanism of quantum dynamical charge transfer allows one to exclude these difficulties in explaining the highly efficient charge transfer over long distances: the electronic wave packet, responsible for the charge transport, spontaneously forms and moves.
It is worth noting that results derived above for the defect-free lattices are also valid for weakly disordered systems. It was numerically verified that the pulse, travelling through the lattice N = 200 with the diagonal disorder W = 1, preserves its shape with rather good accuracy and is well approximated by Eq. (
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 |