Cite this Article
Qiao Yu, Lu Ben-Zhuo. Improvements in continuum modeling for biomolecular systems. Chinese Physics B , 2016, 25(1): 018705  
Permissions
Improvements in continuum modeling for biomolecular systems
Qiao Yu , Lu Ben-Zhuo †,
State Key Laboratory of Scientific and Engineering Computing, Academy of Mathematics and Systems Science, National Centerfor Mathematics and Interdisciplinary Sciences, Chinese Academy of Sciences, Beijing 100190, China

 

† Corresponding author. E-mail: bzlu@lsec.cc.ac.cn

Project supported by the National Natural Science Foundation of China (Grant No. 91230106) and the Chinese Academy of Sciences Program for Cross & Cooperative Team of the Science & Technology Innovation.

Abstract
Abstract

Modeling of biomolecular systems plays an essential role in understanding biological processes, such as ionic flow across channels, protein modification or interaction, and cell signaling. The continuum model described by the Poisson– Boltzmann (PB)/Poisson–Nernst–Planck (PNP) equations has made great contributions towards simulation of these processes. However, the model has shortcomings in its commonly used form and cannot capture (or cannot accurately capture) some important physical properties of the biological systems. Considerable efforts have been made to improve the continuum model to account for discrete particle interactions and to make progress in numerical methods to provide accurate and efficient simulations. This review will summarize recent main improvements in continuum modeling for biomolecular systems, with focus on the size-modified models, the coupling of the classical density functional theory and the PNP equations, the coupling of polar and nonpolar interactions, and numerical progress.

PACS : 87.15.A–
Keyword : Poisson–Boltzmann equation ; Poisson–Nernst–Planck equations ; ionic size effects ; density functional theory
1. Introduction

Modeling of biomolecular systems containing ionic particles and biomolecules is an important approach in life science for investigating the electrostatic properties, such as ion distributions, electrostatic free energy, reactive rate, and ion current. [ 1 – 9 ] Based on a mean field framework, the continuum model treats ions in solution as continuum distributions rather than discrete particles, avoiding large degrees of freedom in computation. In the general case, the Poisson–Nernst– Planck (PNP) equations are utilized for continuum modeling of biomolecular systems. In particular, in the equilibrium state, the ion density is assumed to obey the Boltzmann distribution, and the Poisson–Boltzmann (PB) model can describe the electrostatic interactions in a solvated system. It is noticed that the steady-state PNP equations can be reduced to the PB equation under equilibrium conditions. [ 10 ]

Although the continuum model has wide applications and has achieved great success in predicting many thermodynamic properties, the facts that ions are regarded as point charges and the model does not take into account the ionic volume exclusion and the ion–ion correlations make it unfeasible for systems where these effects are pronounced. [ 11 – 24 ] The continuum model can lead to a high unphysical concentration of counter ions in the vicinity of the biomolecule and miss the phenomena of ionic layering, overcharging or charge inversion, and like-charge attraction. [ 10 , 18 , 25 , 26 ]

In the past few decades, a large number of methods have been developed to improve the continuum model in order to precisely simulate the biomolecular systems and obtain more reasonable computational results. The ionic size effects are incorporated in the continuum model by taking into account the volume exclusion, resulting in a size-modified model. [ 11 – 14 , 16 – 18 ] Combining the classical density functional theory (DFT) with the PNP equations has also been proposed to improve the continuum model through the inclusion of an excess chemical potential, which is the variation of excess Helmholtz free energy with respect to the ion concentrations. [ 20 – 24 , 27 ] Biomolecular exclusion expressed by a characteristic function, as well as other polar and nonpolar interactions, is added to the free energy to obtain optimal volume and surface and minimum free energy. [ 28 – 30 ] Apart from these modifications, some other improvements to account for effects neglected by the traditional continuum models will be briefly discussed.

Along with relevant developments in physics, computer science, and mathematics, numerical methods have also been developed to obtain more accurate and efficient results. [ 1 , 31 ] A new treatment on the boundary is provided to give high solution accuracy and parallelization by using MPI and GPU, and the cilk plus system is used to increase the speed of computations.

The purpose of this review is to provide an overview of the continuum models, their recent improvements, and numerical progress for modeling the biomolecular systems. In Section 2, we discuss the continuum model governed by the PB/PNP equations. The improvements and numerical progress are presented in Section 3 and Section 4, respectively. Finally, we provide the conclusions in Section 5.

2. Continuum model

In the simulation of solvated biomolecular systems, the computational region Ω is composed of two parts, the biomolecular region Ω m with dielectric constant ɛ m , and the solution region Ω s with dielectric constant ɛ s . Figure  1 schematically illustrates such a system, in which Γ denotes the interface between the two different regions and ∂ Ω stands for the outer boundary of the whole system. [ 1 ]

Fig. 1. Illustration of a solvated biomolecular system.

The PB equation in Ω takes the form

where ϕ ( x ) is the potential needed to be solved, ɛ ( x ) = ɛ x ɛ 0 represents the dielectric permittivity in which ɛ x is the relative permittivity at the given point x , and ɛ 0 is the vacuum permittivity, K is the number of ion species in the solution, the characteristic function λ is 0 in Ω m and 1 in Ω s , c b i is the bulk concentration of the i -th ion species with charge q i , β is 1/( k B T ) with k B being the Boltzmann constant and T being the absolute temperature, , and Q i is the singular charge located at x i representing one of the N atoms in the biomolecule. On the interface Γ, two conditions need to be satisfied: (i) ϕ s = ϕ m and (ii) ɛ s ∂ ϕ s / ∂n = ɛ m ∂ϕ m / ∂n , where n is the outer unit vector of Γ. For the outer boundary ∂ Ω far away from the biomolecule, the Dirichlet boundary condition ϕ | ∂ Ω = 0 is commonly used.

In the general case, the PNP equations are given as follows:

where

D i ( x ) is the diffusive coefficient, , and c i ( x ) is the concentration of the i -th ion species at position x . It is not difficult to find that the Boltzmann distribution can be derived from the Nernst–Planck equation (Eq. ( 2 )) under equilibrium conditions where J i ( x ) is zero everywhere. Taking this distribution into the Poisson equation (Eq. ( 3 )), we can obtain the PB equation given in Eq. ( 1 ). In addition to describing the equilibrium conditions of the solvated biomolecular systems, the PNP equations can also model electrodiffusion processes, such as electro-diffusion reactions of mobile ions and charged ligands, and ion transport across channels. [ 7 , 8 , 10 , 17 ] Schematic illustrations of the electro-diffusion processes are presented in Fig.  2 . Similar to the PB model, all the mobile ions and charged ligands are modeled as diffusive particles with vanishing sizes. A small patch Γ a of Γ is specified to model the active site where the chemical reaction occurs, and the zero Dirichlet boundary condition is set for the reactive ion, while the other boundary conditons are the same as the equilibrium boundary settings. [ 6 , 10 ] The solvated system can be constrained in a spherical region, whereas the channel system is simulated in a cubic box.

Fig. 2. Illustrations of (a) a solvated biomolecule with active sites and (b) a channel system.

In biomolecular systems, the concrete form of the free energy is given by

where ρ = ρ f + ρ ion , Λ i is the thermal de Broglie wavelength, and μ i is the chemical potential of the i -th ion species. The potential in this functional is determined from the constraint of the Poisson equation (Eq. ( 3 )); thus the functional depends only on the ion concentrations. Under equilibrium conditions that minimize the free energy, we can derive the Boltzmann distribution and the chemical potential, resulting in the PB equation [ 32 – 34 ] and the free energy form given in Ref. [ 4 ].

3. Improvement of continuum model
3.1. Size-modified PB/PNP model

To consider the ionic size effects in ionic liquids, Andelman et al. modified the free energy form by introducing an additional solvent entropy term representing the unfavorable energy modeling the overpacking or crowding of ions and solvent molecules [ 14 ]

where a 0 is the size of water molecule, and a i is the size of the i -th ion species. By supposing that the sizes of different ion species and water molecules are identical, the ion concentrations at equilibrium state can be expressed as explicit functions of the electrostatic potential through variation of free energy with respect to concentration, which then leads to a size-modified PB model (SMPB). [ 14 ] For a 1 : z asymmetric solution with no fixed charge, the SMPB equation is

Andelman et al. proved that the modified PB equation can be obtained from both the mean-field approximation of the partition function in a formal lattice gas formalism and the including of an entropy term for the solvent molecules in the free energy in an alternative phenomenological approach. [ 35 ] A great decrease in the counter ion concentration is shown in their numerical simulations for a planar surface model and the oversaturation phenomenon is prohibited. Fenley’s team studied this SMPB model through comparing predictions between this equation and the nonlinear PB (NPB) equation for a lowdielectric charged spherical cavity in an aqueous salt solution and investigating the sensitivities to parameterization. [ 16 , 36 ]

To account for different ionic sizes, Chu et al . extended this model to include two different sizes and gave an explicit SMPB form in the study of ion binding to DNA duplexes. [ 15 ] All the explicit forms are obtained by substituting the ion concentration of Boltzmann distribution in the PB equation with an explicit form of modified concentration after considering the ionic volume exclusion. However, an explicit form of an ion concentration as a function of the potential and ionic sizes does not exist for a general case with various ionic and solvent molecular sizes. Because the PB model (equilibrium description) can be considered as a specific case of the PNP model (non-equilibrium description), we can resort to the sizemodified PNP framework to implicitly obtain the SMPB results. We have modified the steady-state PNP equations to obtain nonuniform size-modified PNP (SMPNP) equations that naturally treat arbitrary number of ion species with different sizes and can describe both equilibrium state (i.e., PB case) and non-equilibrium processes of ionic solutions. [ 10 , 17 ] The chemical potential from the variation of the free energy in Eq. ( 6 ) is used for constructing the ion flux from constitutive relations between flux and chemical potentials

where m i is the mobility of the i -th ion species. Substituting this J i in the NP equations given by Eq. ( 2 ), we obtain the modified NP equations of an SMPNP model

where , and the Poisson equation remains the same as given in Eq. ( 3 ).

3.2. Coupling of classical density functional theory and the PNP model

The classical DFT, a systematical theory to investigate inhomogeneous fluids, can be coupled with the PNP equations to improve simulation results for biomolecular systems. The major issue with DFT lies in the construction of an excess Helmholtz free energy. [ 37 ] The fundamental measure theory (FMT), derived by Rosenfeld, provides an excellent suggestion on how to construct the excess Helmholtz free energy for inhomogeneous hard sphere mixtures and has been developed and widely used in many studies. [ 21 , 38 – 46 ] According to the theory, [ 38 ] the excess Helmholtz free energy due to the hard sphere repulsion is given as follows:

where is a set of characteristic (weight) functions for α = 0, 1, 2, 3, V 1, V 2. For a three-dimensional sphere of radius R i , these functions are defined by

Here θ ( x ) is the unit step function

and δ ( x ) is the Dirac delta function.

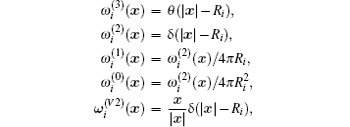
In addition to the ideal chemical potential , an excess chemical potential derived from the variation of the excess free energy defined in Eqs. ( 10 ) and ( 11 ) is introduced to account for the hard sphere interactions

The ion flux is then modified to and the coupling finally yields the following modified NP equations:

It is clear that integro-differential equations are evoked when FMT is incorporated into the PNP equations, which contain a large number of freedoms and are quite difficult for numerical implementation in real biomolecular simulations. For simplicity, most numerical experiments are constrained to the 1D case or use the definition of the Dirac delta function and change of variables to transform these 3D integrals into 2D integrals on spheres to remove the singularity in the integrands. [ 20 , 21 , 24 ] Only a few studies have provided 3D algorithms and performed calculations on 3D cases without biomolecules using fast Fourier transform to cope with the convolutional integrations. [ 22 , 23 ]

In contrast to the integral form of the excess chemical potential and the above mentioned efforts to solve the integrodifferential equations, Liu et al . have derived a local hard sphere description for in the 1D case, given by

where d j is the diameter of the j -th ion species. [ 46 ] To obtain more accurate simulations of biomolecular systems, we have incorporated a local excess chemical potential originating from the 3D hard sphere interactions [ 27 ]

into the PNP model to form a local hard sphere PNP (LHSPNP) model that can capture the ionic finite size and the excluded volume effects featured by the saturation phenomenon but simplify the numerical calculations at the same time. The first term in Eq. ( 16 ) is similar to the excess chemical potential in the SMPNP model where . Furthermore, similarities between the numerical results of these two models are also observed under most boundary conditions.

In addition to the chemical potential due to hard sphere repulsions, chemical potential terms resulting from electrostatic correlations and short-range attraction interactions have also been analyzed in many studies. [ 22 , 23 , 43 ] There are also some improvements in the FMT to account for discrete particle interactions. Kierlik and Rosinberg proposed a simplified version of the FMT, which was proven to be equivalent to the original FMT but required only four scalar weight functions. [ 45 ] Using the Mansoori–Carnahan–Starling–Leland bulk equation of state, Roth et al . and Wu et al . independently published the white-bear version or the modified FMT to make simulation results more accurate. [ 40 , 42 ] For inhomogeneous fluids of nonspherical hard particles, Mecke et al . derived a fundamental measure theory using the Gauss–Bonnet theorem. [ 44 ] These different forms of the excess Helmholtz free energy lead to different expressions of the excess chemical potential and thus different coupling results of DFT and PNP.

3.3. Coupling polar and nonpolar interactions

Polar and nonpolar interactions are coupled. In recent years, a few groups used a variational framework to study the coupled system. [ 28 – 30 , 47 ] In particular, in the studies pertaining to Refs. [ 28 ]–[ 30 ], the biomolecular surface (interface between solute and solvent) was not fixed, but determined as a model output. A variational model was proposed under the consideration of an assembly of solutes with arbitrary shape and composition surrounded by a dielectric solvent in a macroscopic volume to explicitly couple hydrophobic, dispersion, and electrostatic contributions in a continuum model. The typical free energy, including volume energy, surface energy, van der Waals interaction energy, and continuum electrostatic free energy, is expressed as a functional of the characteristic function ν

where P is the pressure difference between the liquid and vapor, ν ( x ) is 0 in space without solvent and 1 elsewhere, U VDW ( x , c w ( x ), { c i ( x )}) is the solvent–solute and/or solvent–solvent van derWaals interactions (model dependent), and c w ( x ) is the water molecular concentration. Optimal volume and surface are obtained via minimization of the free energy. Li et al . provided a representation of the interface by a phase field and expressed the free energy by all possible phase fields. [ 29 ] The equilibrium conformations and free energies of an underlying molecular system were determined by the variational principle. Wei used the differential geometry theory of surfaces for geometric separation of the macroscopic domain of the solvent from the microscopic domain of the solute, and for dynamical coupling of the continuum and discrete descriptions, to investigate multiscale multi-physics and multi-domain models. [ 30 ] The free energy functional can also properly include other energy terms from quantum mechanics, fluid mechanics, molecular mechanics, and elastomechanics, which will lead to more complicated models.

3.4. Other improvements

In addition to the above improvements, some other modifications have also been made to the continuum model. The homogeneous assumption of dielectric medium does not coincide with the experimental results of salt water solutions. [ 48 ] We explored a variable dielectric PB (VDPB) model by considering the dielectric as an explicit function of ionic sizes and concentrations. [ 25 ] Andelman et al . proposed a dipolar PB (DPB) model by coarse graining the interaction of individual ions and dipoles. [ 49 ] A Poisson–Fermi model was derived by introducing a fourth-order free energy functional to describe the interplay between overscreening and crowding. [ 13 , 19 ] Other modifications, for example, incorporating image charge effects [ 50 ] and Lennard–Jones hard sphere repulsion [ 24 ] into the primitive model, have also been studied to improve the continuum model. Horng et al . introduced the finite size effect by treating ions and side chains as solid spheres and using Lennard–Jones hard sphere repulsion potentials to characterize this effect, and observed the ion-selectivity behavior in a simple 1D analysis and simulation. [ 47 ]

Other beyond-mean-field models have been developed at the same time to account for the ion–ion correlations. Kjellander et al . introduced the dressed ion theory, a formally exact theory for electrolyte solutions and colloid dispersions by writing the ion–ion correlation function as a sum of a shortrange part and a (relatively) long-range part. [ 51 , 52 ] For nucleic acid mixtures, the tightly bound ion theory was presented by Tan et al ., which catures the fluctuations and the electrostatic and ion–ion correlations and provides reliable predictions for ion distributions and thermodynamic properties. [ 53 , 54 ] The integral equation theory was used to evaluate the distribution functions of solvents and ions and calculate the liquid structure and thermodynamic properties. [ 55 – 59 ] In case of high valence ions, a strong coupling theory as a correction to the PB approach is available to predict the counter ion distributions around charged objects. [ 60 ] Furthermore, a system of self-consistent partial differential equations has been derived to extend the PB equation to include the electrostatic correlation and fluctuation effects, [ 12 , 61 ] and recently a numerical method was developed to solve the equations. [ 62 ]

4. Numerical progress

In the simulation of biomolecular systems, progress has been made for developing more accurate and efficient algorithms. [ 1 , 31 ] In the finite difference method for the PB equation, to enforce the interface conditions and to obtain better numerical convergence, Wei et al . implemented the matched interface and boundary (MIB) method to accurately treat the interface conditions, and also used the regularization scheme described in Ref. [ 63 ] to remove the charge singularities in the molecule to achieve a higher level of accuracy. [ 64 , 65 ] Luo’s group developed the immersed interface method (IIM), a new discretization method, and implemented it in the PBSA solver incorporated in the Amber package. [ 66 ] Lu et al . used the finite element method and a body-fitted molecular surface mesh to solve the interface problem with a high level of accuracy. [ 1 , 7 ] At the same time, considerable efforts have been made to increase the speed of computations. Xie et al . employed the MPI to present a parallel adaptive finite element algorithm to solve the 3D electro-diffusion equations. [ 8 ] Geng et al . provided a GPU-accelerated direct-sum boundary integral method to solve the linear PB equation. [ 67 ] Yokota et al . presented a GPU-accelerated algorithm with the fast multipole method in conjunction with a boundary element method (BEM) formulation, resulting in strong scaling with parallel efficiency of 0.5 for 512 GPUs. [ 68 ] Lu et al . parallelized the adaptive fast multipole PB (AFMPB) package with the cilk plus system to harness the computing power of both multicore and vector processing, which achieved nearly optimal computational complexity in BEM and successfully solved on a workstation the PB equation for macromolecular systems such as a virus with tens of million degrees of freedom. [ 69 ]

5. Conclusions

We have summarized the PB/PNP types of continuum models based on the mean field approximation, their improvements to include the ionic size effects, other physical properties that have been missed in the previous models, the coupling of polar and nonpolar interactions, and numerical progress for biomolecular simulations. The main improvements for including the size effects are achieved by introducing an excess chemical potential term to account for discrete particle interactions ignored in the continuum model. However, differing from the SMPB/SMPNP models which are still based on mean field approximations, coupling of DFT and PNP provides a reliable framework for particle interactions. The variational treatment of the biomolecular surface is included in the free energy that couples polar and nonpolar interactions to obtain both an optimal surface and a minimum free energy. Numerical progress makes it possible to obtain more accurate and efficient algorithms for simulating biomolecular systems. It is expected that much effort will be made in the future for developing beyond-mean-field continuum models that can not only capture important detailed physical effects but also keep numerically tractable for biomolecular systems. At the same time, effective numerical techniques (along with advances in modern computer science and mathematics) need to be developed for dealing with larger and more complicated simulation systems.

Reference
1 Lu B Zhou Y Holst M McCammon J 2008 Commun. Comput. Phys. 3 973
2 Baker N 2005 Biomolecular Applications of Poisson-Boltzmann Methods Hoboken John Wiley & Sons, Inc. 349 379
3 Fogolari F Brigo A Molinari H 2002 J. Mol. Recognit. 15 377
4 Gilson M Davis M Luty B McCammon J 1993 J. Phys. Chem. 97 3539
5 Sharp K Honig B 1990 J. Phys. Chem. 94 7684
6 Lu B Zhou Y Huber G Bond S Holst M McCammon J 2007 J. Chem. Phys. 127 135102
7 Tu B Chen M Xie Y Zhang L Eisenberg B Lu B 2013 J. Comput. Chem. 34 2065
8 Xie Y Cheng J Lu B Zhang L 2013 Mol. Based. Math. Biol. 1 90
9 Pods J Schönke J Bastian P 2013 Biophys. J. 105 242
10 Lu B Zhou Y 2011 Biophys. J. 100 2475
11 Vlachy V 1999 Annu. Rev. Phys. Chem. 50 145
12 Netz R Orland H 2000 Eur. Phys. J. E 1 203
13 Bazant M Storey B Kornyshev A 2011 Phys. Rev. Lett. 106 046102
14 Borukhov I Andelman D Orland H 1997 Phys. Rev. Lett. 79 435
15 Chu V Bai Y Lipfert J Herschlag D Doniach S 2007 Biophys. J. 93 3202
16 Silalahi A Boschitsch A Harris R Fenley M 2010 J. Chem. Theory Comput. 6 3631
17 Qiao Y Tu B Lu B 2014 J. Chem. Phys. 140 174102
18 Li B Liu P Xu Z Zhou S 2013 Nonlinearity 26 2899
19 Liu J 2013 J. Comput. Phys. 247 88
20 Gillespie D Nonner W Eisenberg R 2002 J. Phys.: Condens. Matter 14 12129
21 Ji S Liu W 2012 J. Dyn. Differ. Equat. 24 955
22 Meng D Zheng B Lin G Sushko M 2014 Commun. Comput. Phys. 16 1298
23 Knepley M Karpeev D Davidovits S Eisenberg R Gillespie D 2010 J. Chem. Phys. 132 124101
24 Hyon Y Eisenberg B Liu C 2011 Commun. Math. Sci. 9 459
25 Li H Lu B 2014 J. Chem. Phys. 141 024115
26 Allahyarov E Gompper G Löwen H 2004 Phys. Rev. E 69 041904
27 Qiao Y Lu B Chen M 2016 J. Statistical Physics in press
28 Dzubiella J Swanson J McCammon J 2006 Phys. Rev. Lett. 96 087802
29 Zhao Y Kwan Y Che J Li B McCammon J 2013 J. Chem. Phys. 139 024111
30 Wei G 2013 J. Theor. Comput. Chem. 12 1341006
31 Li C Li L Petukh M Alexov E 2013 Mol. Based. Math. Biol. 1 42
32 Fogolari F Briggs J 1997 Chem. Phys. Lett. 281 135
33 Li B 2009 SIAM J. Math. Anal. 40 2536
34 Jadhao V Solis F J Olvera de la Cruz M 2013 Phys. Rev. E 88 022305
35 Borukhov I Andelman D Orland H 2000 Electrochim. Acta 46 221
36 Harris R Boschitsch A Fenley M 2014 J. Chem. Phys. 140 075102
37 Evans R 2009 Lectures at 3rd Warsaw School of Statistical Physics, Kazimierz Dolny 27
38 Rosenfeld Y 1989 Phys. Rev. Lett. 63 980
39 Rosenfeld Y Levesque D Weis J 1990 J. Chem. Phys. 92 6818
40 Roth R Evans R Lang A Kahl G 2002 J. Phys.: Condens. Matter 14 12063
41 Roth R 2010 J. Phys.: Condens. Matter 22 063102
42 Yu Y Wu J 2002 J. Chem. Phys. 117 10156
43 Jiang J Cao D Jiang D Wu J 2014 J. Phys.: Condens. Matter 26 284102
44 Goos H Mecke K 2009 Phys. Rev. Lett. 102 018302
45 Kierlik E Rosinberg M 1990 Phys. Rev. A 42 3382
46 Lin G Liu W Yi Y Zhang M 2013 SIAM J. Appl. Dyn. Syst. 12 1613
47 Horng T Lin T Liu C Eisenberg B 2012 J. Phys. Chem. B 116 11422
48 Hasted J Ritson D Collie C 1948 J. Chem. Phys. 16 1
49 Abrashkin A Andelman D Orland H 2007 Phys. Rev. Lett. 99 077801
50 Gan Z Xu Z 2011 Phys. Rev. E 84 016705
51 Kjellander R Mitchell J 1992 Chem. Phys. Lett. 200 76
52 Kjellander R 2001 Distribution Function Theory of Electrolytes and Electrical Double Layers Heidelberg Springer Netherlands 317 366
53 Tan Z Chen S 2005 J. Chem. Phys. 122 044903
54 Tan Z Chen S 2009 Predicting Electrostatic Forces in RNA Folding 465
55 Ikeguchi M Doi J 1995 J. Chem. Phys. 103 5011
56 Beglov D Roux B 1995 J. Chem. Phys. 103 360
57 Vrbka L Lund K Kalcher I Dzubiella J Netz R Kunz W 2009 J. Chem. Phys. 131 15109
58 Giambasu G Luchko T Herschlag D York D Case D 2014 Biophys. J. 106 883
59 Zwanikken J W Olvera de la Cruz M 2013 Proc. Natl. Acad. Sci. USA 110 5301
60 Moreira A Netz R 2000 Europhys. Lett. 52 705
61 Avdeev S Martynov G 1986 Colloid J. USSR 48 535
62 Xu Z Maggs A 2014 J. Compt. Phys. 275 310
63 Chern I Liu J Wang W 2003 Methods Appl. Anal. 10 309
64 Zhou Y Zhao S Feig M Wei G 2006 J. Comput. Phys. 213 1
65 Geng W Yu S Wei G 2007 J. Chem. Phys. 127 114106
66 Wang C Wang J Cai Q Li Z Zhao H Luo R 2013 Comput. Theor. Chem. 1024 34
67 Geng W Jacob F 2013 Comput. Phys. Commun. 184 1490
68 Yokota R Bardhan J Knepley M Barba L Hamada T 2011 Comput. Phys. Commun. 182 1272
69 Zhang B Peng B Huang J Pitsianis N Sun X Lu B 2015 Comput. Phys. Commun. 190 173