Lithium-ion transport in inorganic solid state electrolyte
[Gao Jian 1, 2 , Zhao Yu-Sheng 3 , Shi Si-Qi 4, 2, †, 
, Li Hong 1, ‡, ]
, Li Hong 1, ‡, ]
Cite this Article 
Gao Jian, Zhao Yu-Sheng, Shi Si-Qi, Li Hong. Lithium-ion transport in inorganic solid state electrolyte. Chinese Physics B , 2016, 25(1): 018211 
Permissions
Lithium-ion transport in inorganic solid state electrolyte
† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 51372228), the Shanghai Pujiang Program, China (Grant No. 14PJ1403900), and the Shanghai Institute of Materials Genome from the Shanghai Municipal Science and Technology Commission, China (Grant No. 14DZ2261200).
Abstract
Abstract
An overview of ion transport in lithium-ion inorganic solid state electrolytes is presented, aimed at exploring and designing better electrolyte materials. Ionic conductivity is one of the most important indices of the performance of inorganic solid state electrolytes. The general definition of solid state electrolytes is presented in terms of their role in a working cell (to convey ions while isolate electrons), and the history of solid electrolyte development is briefly summarized. Ways of using the available theoretical models and experimental methods to characterize lithium-ion transport in solid state electrolytes are systematically introduced. Then the various factors that affect ionic conductivity are itemized, including mainly structural disorder, composite materials and interface effects between a solid electrolyte and an electrode. Finally, strategies for future material systems, for synthesis and characterization methods, and for theory and calculation are proposed, aiming to help accelerate the design and development of new solid electrolytes.
Keyword : lithium-ion batteries ; solid state electrolyte ; ionic conductivity ; ion transport mechanism
1. Introduction
The early definition of solid state electrolytes (SSE) is usually indistinguishable from fast ion conductors (FICs) or super ion conductors (FICs), which are grouped as solid materials with ionic conductivity approaching (or in some cases exceeding) that of molten salts or electrolytic solutions. This implies a peculiar liquid-solid dual property, i.e., “some atoms have nearly liquid like mobility while others retain their regular crystalline arrangement.” [ 1 ]
With the great attention paid to lithium-ion batteries (LIBs), their potential applications in electric vehicles and large-scale smart grids demand an urgent enhancement of safety, which results in today’s broadened interest in inorganic solid state electrolytes. Some of their issues are as follows: (i) Composite solid electrolytes have higher conductivity at interphases. (ii) Solid electrolyte interphase (SEI) growing on electrodes (especially anions) is of critical importance for the performance of LIBs. However, Li 2 CO 3 , the main inorganic component, has much lower conductivity than the first defined superionic conductors. [ 2 – 5 ] In addition, electrode coatings, coreshell electrode particles and self-organized surfaces formed during synthesis also have functions similar to SEI. (iii) The conductivity of LiPON is of the magnitude 10 −6 S/cm, which is much lower than found before; however, a thin film allsolid- state cell structure enables over 30000 charge–discharge cycles. [ 6 ] Considering all of the above, the general discussion of solid state electrolytes in this review is focused on their role in a working cell (to convey ions while isolating electrons), but not for their conductivity and the ion transport mechanism.
This review will concentrate on the ion diffusion mechanism in inorganic solid state matter, and the ion diffusion in polymers is mentioned as an aside to clarify the perspective. Although the review will focus on solid state electrolytes working in LIBs, the theoretical models and treating processes can be applied to those working in fuel cells, solid oxide fuel cells (SOFC), Li–air batteries, Li–S batteries, electrochemical sensors, electrochromic devices, oxygen separation membranes, and so on.
The superionic phase can typically be distinguished from the usual phase because of the following properties, which are summarized in Ref. [ 1 ]: high ionic conductivity, low activation, an open structure with an interconnected network of vacant sites available to ionic species. Besides, the phase can be characterized by dynamic and collective effects: the absence of well-defined optical lattice modes, the presence of a pervasive, low-energy excitation, an infrared peak in the frequencydependent conductivity, unusual NMR prefactors, phase transitions and a strong tendency for mobile ions to be found between allowed sites. High ionic conductivity often conflicts with high structural stability, because higher ionic conductivity requires weak chemical bonding energy, which leads to opposite effects on the structural stability. As a compromise between the two aspects, a sort of “dual structure” will work: two separate sub-lattices provide, respectively, a rigid frame and a soft part that may undergo the phase transition to the higher symmetrical characteristic structure (disordered state) for mobile ions.
Atypical ionic conductors without “dual structure” or independent superionic phase can also be of interest as solid state electrolytes, as defined and interpreted above. Their characteristics usually lie between the normal thermally activated defect crystals and typical superionic conductors. Moreover, atypical ones often exist as thin film with nanometer scale thickness to make up for their deficient conductivity. Then the complexity of defects gives rise to the challenges of theoretical models and experimental characterization.
2. Brief history of the development of solid electrolytes [ 7 – 11 ] 1 ) is replaced with ( n + n ′ − αnx − x c ) μ , where n and n′ are the respective numbers of Li atoms and vacancies in the crystal lattice unit. [ 151 ] Besides, the 2D conduction mechanism is found at relatively lower temperature directly by neutron powder diffraction study, [ 152 ] while higher temperatures increase the oxygen vibration and open up the originally blocked bottleneck to enable the third dimension for Li-ion diffusion [ 153 ] and delocalizes Li ions from the 2D La-poor layer to realize a higher degree of disorder. [ 154 ] Considering the quasi-2D conduction mechanism and the preferential La distribution, equation ( 1 ) can be further revised as: σ ∝ n eff ( n ′ − n c ) μ = 12 x (1 − 12 x )(0.5 − g (La2)) 1.3 . [ 152 ] The deviation from Arrhenius can be explained by the long-range correlation of mobile carriers, which can be inferred both from the abnormal activation energy measured by IS. [ 153 , 155 ] as well as from activation energy discrepancies between IS and measurements of 7 Li NMR spin-lattice relaxation. [ 156 ] The total conductivity of Li 3 x Ln 2/3− x [U + FFFF] 1/3−2 x TiO 3 is limited by grain boundary resistance, which can be reduced by high temperature sintering; however, the high-temperature, long-duration thermal process leads to Li evaporation, making accurate control of Li content difficult. Therefore, this system can hardly be applied in all-solid-state batteries.
In 1833, Michael Faraday discovered an abnormal enhancement of electrical conductivity in Ag 2 S with the stimulation of temperature that could not be interpreted as arising from electronic conductivity. He then proposed Faraday’s laws of electrolysis. [ 12 ] After that, Faraday, [ 13 ] Hittorf, [ 14 ] Gaugain, [ 15 ] etc. found that many inorganic solids exhibit similar behaviors. In 1884, Warburg [ 16 ] tested and verified Faraday’s laws of electrolysis, and this work is regarded as a significant breakthrough for putting forward the probability of ionic (other than electronic) conductivity, overturning the conclusion of Arrhenius that neither pure salt nor pure water can be a conductor, but only salt dissolved in water.
In 1897, Nernst invented stabilized ZrO 2 as an electric lighting device (Nernst glower), [ 17 , 18 ] and it is still one of the most important oxygen sensitive solid electrolyte materials. The flow of electrical current was suggested to be essentially oxygen ion conduction, although the underlying mechanism was not illustrated until 1943 by Wagner. [ 19 ] During the period, Haber, [ 20 ] Katayama, [ 21 ] etc. actively promoted the investigation of glass/ceramic solid state electrolytes. In 1935, on the basis of the stabilized ZrO 2 discovered by Nernst, Schottky applied for the first patent on solid electrolytes used for fuel cells. [ 22 ] Subsequently, several other solid electrolytes suitable for fuel cell were proposed by Baur and Priess. [ 23 ] The performance of stabilized ZrO 2 was not surpassed until the 1960s, when Takahashi discovered CeO 2 –La 2 O 3 solid solutions. [ 24 ] Nowadays, materials mentioned above remain the most widely utilized in SOFCs.
Other than the oxygen ion conductors mentioned above, in 1914, Tubandt and Lorenz studied the silver and thallium halides, among which AgI is important for its phase transition to high-conductive α -AgI below the melting point, exhibiting conductivity similar to its liquid phase. [ 25 ] The mobility was measured to identify Ag ions other than electrons as mobile species. [ 26 ] In 1935, by means of x-crystallography, strock studied the structure and put forward the sublattice melting model to interpret the abnormal high conductivity for Ag ions. [ 27 ]
On the theoretical side, the ion diffusion mechanism cannot be separated from defect chemistry. In 1923, Joffé concluded that “even pure crystals are partly dissociated and present an intrinsic conductivity”; [ 28 ] in 1926, by assuming the presence of point defects, Frenkel suggested two basic diffusion mechanisms through interstitials and vacancies separately. [ 29 ] In 1930, Wagner and Schottky deduced from statistical thermodynamics that “in equilibrium at a finite temperature, some defects exist, even in a crystal of exact stoichiometric composition.” In addition, nonstoichiometricity of a compound, i.e., having an excess of some component, can lead to extra interstitials or vacancies. [ 30 , 31 ] In 1962,Wagner extended the concepts of defect chemistry to the multicomponent system. [ 32 ] On the experimental side,Wagner contributed quite a lot during the 1950s, including the Hebb– Wagner direct-current polarization technique. And Wagner and Hebb proposed “blocking electrodes”, electrodes that can distinguish the partial ionic and electronic current carriers of mixed conductors. [ 33 ]
At the end of the 1960s, some novel inorganic solid electrolytes were obtained via innovative synthesis strategies, and they attracted much attention due to their high conductivity and potential applications in electrochemical devices such as batteries. Two successful attempts were the synthesis of RbAg 4 I 5 via doping, and stabilizing the high-temperature, high-conductivity phase α -AgI at room-temperature. [ 34 ] In another breakthrough, the Cu ion conductor Rb 4 Cu 16 I 7 Cl 13 was synthesized and is even now the solid electrolyte with highest conductivity. [ 35 ] In 1973, Kunze discovered fast ion-conduction behavior in a glassy system with Ag, [ 36 ] which leaped over the earlier limitations of ceramic fields. While their conductivity is quite high, the above compounds are expensive, due to their Ag constituent and their Gibbs free energy is too low, causing low energy capacity at open-circuit voltage. Moreover, composition with excess Cu is usually accompanied by electrons or holes generating current, leading to mixed conductors, rather than a pure Cu ion conductor. As a result, neither Ag nor Cu ionic conductors can satisfy the application requirements.
In view of the above situation, attention was gradually turned to the alkali metal solid state electrolytes. In 1967, β -Al 2 O 3 was found to be a solid electrolyte with two-dimensional conduction pathways, [ 37 ] and it reached the apex of its reputation with the coming of the American oil crisis, when it was successfully applied in Na–S batteries. As an alternative to organic electrolyte solutions, solid state electrolytes are safer, so they have huge application prospects, motivating the investigation of solid state ionics.
Lithium is the lightest alkali metal with the smallest atomic number, indicating an extremely high gravimetric energy density, which attracts much attention, although the Li–ion solid electrolyte shows lower gravimetric energy density than the Ag or Cu counterpart, as shown in Figs. Research progress map of solid electrolytes (adapted from Ref. [ 8 ], LiRAP is added). Arrhenius plot of available lithium solid electrolytes, organic liquid electrolytes, polymer electrolytes, ionic liquids, and gel electrolytes. [ 38 ]
Lithium nitride was first reported in 1935, [ 39 ] and became intriguing as an ion conductor for its high lithium content and its open structure. [ 40 , 41 ] In 1973, Liang dispersed Al 2 O 3 particles into a LiI solid matrix, and obtained a mixture with conductivity 50 times higher than that of LiI alone. [ 42 ] The “space charge layer” theory was proposed by Wagner [ 43 ] and Maier [ 44 ] in succession to interpret the abnormal phenomenon, guiding followers to optimize conductivity by designing the micro- or nano-complex. In 1980, LiI was used as a solid electrolyte in commercializing cardiac pacemakers. [ 45 ] In 1981 and 1982, lithium halide hydrate solid state electrolytes with an anti-perovskite structure were proposed, [ 46 – 48 ] as was their mixture with Al 2 O 3 . [ 49 ] Besides, LiBH 4 [ 50 , 51 ] (and the mixture with lithium halides [ 52 ] ) has high conductivity. The decomposition voltage of lithium-ion nitrides and iodides is too low to satisfy one of the usual criteria, which requires a really high cathode voltage involved in lithium-ion secondary batteries for high energy capacity. Despite the intrinsic disadvantage of instability, these discoveries and potential applications stimulated enthusiasm for researching inorganic solid state electrolytes, which motivated the discovery of oxide and sulfide systems with wider electrochemical windows and higher chemical and electrochemical stability.
Early attempts with lithium-ion oxide salts did not result in adequate performance as solid state electrolytes. [ 53 , 54 ] In 1976, Goodenough and Hong were first to report a fast sodium ion conductor Na 1+ x ZrP 3− x Si x O 12 , which was later named NASICON (Na superionic conductor). [ 3 , 55 , 56 ] In 1977, Li M 2 (PO 4 ) 3 compounds with the same structure and general formula as Li M I M II P 3 O 12 were found to have high conductivity. [ 57 ] The three-dimensional (3D) [ M I M II P 3 O 12 ] skeleton of NASICON is composed of MO 6 octahedra linked to PO 4 tetrahedra; mobile Li ions are distributed in skeletons with two types of occupied sites ( A 1 , A 2 ). The Li ion must struggle through a bottleneck when it jumps between two sites, and the bottleneck size depends greatly on the types and character of skeleton ions, [ 58 ] and is influenced by the distribution or concentration of mobile ions at sites ( A 1 , A 2 ). [ 59 ] The abundant variety of dopants and substitutes makes NASICON a typical case for studying the relationship among chemical composition, crystal structure and ionic conductivity. [ 60 ] For example: if M is Ti, then Ti can be doped with Mg, In, Ga, Sc, Al, La, Y, Sn; [ 61 – 67 ] if M is Zr, then Zr can be doped with Nb, Ta, Y, In; [ 68 ] if M is Ge, Ge can be doped with Al, Ga, Sc, In, [ 69 , 70 ] and if M = Hf, then Hf can be doped with In, Sc. [ 71 – 73 ] Among all possible compounds, Li 1.3 Al 0.3 Ti 1.7 (PO 4 ) 3 has the highest conductivity, whose M is fixed to Ti and doped by Al. [ 65 , 66 ] Although there have been many studies on NASICON superionic conductors, the inherent reasons for the doping-induced enhancement of ionic conductivity still remain open. Aono suggested that the high conductivity of Li 1.3 Al 0.3 Ti 1.7 (PO 4 ) 3 may not be determined by the intrinsic structural character, but contributed by the higher density and smaller grain boundary resistance, which are both due to the Al doping. [ 74 ] The shortcoming of the large grain boundary resistance for the NASICON system can be overcome by preparing it into lithium-ion conductive glass ceramics (LIC-GC). [ 75 – 77 ] LIC-GC enhances total ionic conductivity by eliminating grain boundary resistance and is relatively easy to fabricate at a large scale by a melting method. In addition, glassy products are easier to mold and can be shaped into thin films. Note that LIC-GC has already been commercialized by the OHARA company. [ 78 ]
Another Li superionic conductor (LISICON) with 3D conduction pathway, Li 14 Zn(GeO 4 ) 4 , was developed by Hong in 1978. [ 79 ] However, the pure solution phases for this kind of oxysalt can be formed only within limited ranges of concentration and temperature. [ 80 ] The general formula is extended to x Li 4 M IV O 4 –(1 − x )Li 3 M V O 4 ( M IV = Ge, Ti, M V = As, V) as a γ -Li 3 PO 4 -type solid electrolyte, which also has the solid solution limit ( x = 0.4–0.6), and conductivity is not more than 10 -4 S/cm. [ 81 ] Benefitting from the development of computer science and information techniques, it is feasible to screen solid state electrolytes for those possibly having excellent performance, via high throughput calculation. Fujimura et al. investigated LISICON systematically by calculating a series of conductivities of a wide compositional phase space at high temperature. Together with the machine learning technology, theoretical and experimental datasets are combined to predict the conductivity of each composition at certain temperatures. Limited by the actual solution range, the conductivity of the optimized composition is still less than 10 -4 S/cm. [ 82 ] Although this system has low conductivity, its amorphous film can be applied in thin film batteries [ 83 , 84 ] for a shorter distance and smaller resistance between cathode and anode. Moreover, the glass or glass-ceramic state extension of the system usually has the higher conductivity. In 1993, as another extension of γ -Li 3 PO 4 system, [ 85 ] the thermodynamically stabilized LiPON thin film was fabricated with radio frequency (RF) sputtering by Bates et al. [ 86 ] LiPON thin film has been widely used as thin film solid electrolyte [ 6 , 86 – 90 ] for its wide electrochemical window within 0–5.5 V [ 91 ] and its compatibility with high-voltage cathodes (above 5 V) such as LiN i 0.5 Mn 1.5 O 4 , with a long life of more than 10000 cycles. [ 92 ] The Li 2 PO 2 N crystal was synthesized and calculated by ab initio calculation, comparing it to amorphous LiPON. [ 93 ]
The Thio- γ -Li 3 PO 4 system often has higher conductivity, the study of which has been encouraged by the investigation of glass states of this system. [ 94 ] Highly polarized S ions interact with Li ions weakly, which results in sulfide solid electrolytes having higher conductivity than oxysalts. [ 94 – 98 ] As a result, sulfide solid electrolytes have become the current preference for integration into all-solid-state batteries. [ 99 , 100 ] Although the conductivity can be further increased by adding the composites such as LiI, [ 95 – 98 ] as mentioned above, the low decomposition voltage of LiI narrows the electrochemical window. Further studies indicate that adding oxides to the system can also enhance conductivity without affecting the working voltage, [ 101 , 102 ] and the resulting system can be applied in solid state batteries with 4 V cathodes. [ 103 – 105 ] Besides the glass-state systems, there has been much progress in the research of crystalline-state Li–P–S systems. [ 106 – 108 ] In 2000, Kanno discovered pure sulfides with a structure similar to LISICON, called thio-LISICON. [ 109 ] By optimizing the composition, Li 3.25 Ge 0.25 P 0.75 S 4 was found to exhibit the highest conductivity [ 110 ] among the thio-LISICON compounds. The system includes Li–Ge–P–S, [ 109 – 111 ] Li–Si–P–S, [ 112 , 113 ] and some thin films, [ 114 ] and it can be extended to general γ -Li 3 PS 4 [ 115 ] and β -Li 3 PS 4 [ 116 , 117 ] systems. The general system is one of the most widely investigated as solid state electrolytes, [ 113 , 118 , 119 ] but usually in combination with cathodes of lower voltage than common commercialized cathodes (e.g., LiFePO 4 and LiCoO 2 ) to ensure stability of the system. Besides, similar to the case of NASICON systems, the conductivity of LISICON can be enhanced by crystallizing the glass state to form a glass-ceramic system, [ 120 – 124 ] and the glass-ceramic electrolytes can be used in all-solid-state batteries. [ 125 , 126 ]
It is worth mentioning that in 2011, Kamaya et al. reported that a novel crystalline sulfide state solid electrolyte, Li 10 GeP 2 S 12 , exhibiting conductivity of 1.2× 10 -2 S/cm at room temperature, which is the highest so far among the inorganic solid electrolytes. [ 38 ] It can be applied in all-solid-state batteries incorporating LiCoO 2 as the cathode (in contrast to sulfides mentioned in the last paragraph) [ 38 , 127 ] and Li–In alloy, [ 38 ] Li 4 Ti 5 O 12 , [ 128 ] or Si [ 129 ] as the anode. In addition, it was found that batteries with Li metal as the anode and LiFePO 4 or LiNi 0.5 Mn 1.5 O 4 as the cathode can work, and the corresponding voltammetric profiles were measured, although the cycling performance was not presented. [ 130 ] One possible reason is that Li 10 GeP 2 S 12 is not stable when in contact with Li metal, as has been confirmed by ab initio calculations, [ 131 ] cyclic voltammetry (CV) and ex situ x-ray diffraction (XRD) results. [ 132 ] The crystal skeleton structure was first obtained from XRD and synchrotron radiation x-ray data, combined with ab initio calculation, [ 38 ] and the Li occupation pattern was analyzed from refining the neutron diffraction [ 38 ] and single crystal x-ray data. [ 133 ] Furthermore, the thermodynamic stability of Li 10 GeP 2 S 12 was investigated by ab initio calculation, [ 134 ] and the Li ion diffusion mechanism was studied by classical [ 135 ] and ab initio [ 131 ] molecular dynamic (MD) simulations. Given the strong Coulombic interaction among the mobile ions, the string like cooperative ionic motion pattern is found to be energetically favorable, [ 136 ] leading to a one-dimensional ionic channel with low activation energy and high conductivity. [ 134 , 136 ] Interestingly, the consideration of van der Waals (VdW) interaction resulted in a three-dimensional ionic channel. [ 137 ] Combining two measurement methods with a distinct specific time-scale, AC impedance spectroscopy (IS) and pulsed field gradient NMR (PFG-NMR), the conduction pathway dimension was identified separately according to the time-scale. [ 138 ] A totally different collective diffusion process was observed using nanosecond quantum molecular dynamics simulations of non-stoichiometric Li 4− x Ge 1− x P x S 4 , which leads to drastically reduced activation energy. [ 139 ] Experimental results also indicate higher conductivity, up to 1.42× 10 −2 S/cm, at room temperature for non-stoichiometric Li 10+ δ Ge 1+ δ P 2- δ S 12 (0 ≤ δ ≤ 0.35); in addition, when temperature is increased, the activation energy was reduced, and the respective three- and one-dimensional conduction pathways at high and low temperatures were visualized through the neutron diffraction data refined by the maximum-entropy method (MEM). [ 140 ] Enlightened by the discovery of Li 10 GeP 2 S 12 in 2011, Ong et al. studied the phase diagram, electrochemical stability and ionic conductivity of the Li 10± 1 M P 2 X 12 ( M = Ge, Si, Sn, Al, P, X = O, S or Se) family, finding that smaller lattice parameters lower the conductivity significantly, while larger parameters had less effect. Oxygen-substituted samples are stable, in contrast to their sulfide counterparts with lower conductivity. Note that for wide acceptance, electrolytes containing Ge are usually not stable with Li anodes, and both Si and Sn attract attention as substitutes with cheaper prices. [ 141 ] Before long, both of them (Sn, [ 138 , 142 ] Si [ 129 , 142 , 143 ] ) were authenticated by experiments. By the way, elastic properties of Li 10 GeP 2 S 12 , which are important for practical application as solid state electrolytes, were systematically studied by ab initio calculations. [ 144 ]
Li 3 x Ln 2/3− x [U + FFFF] 1/3−2 x TiO 3 , usually abbreviated as LLTO, presents a definite percolation diffusion mechanism based on Li sites and vacancy sites, because of its simple perovskite structure and obvious intrinsic vacancies arising from the primary Ln 2/3 [U + FFFF] 1/3 TiO 3 . When Ln is doped by Li, the original vacancies are occupied by excess Li as charge compensation. The discovery of perovskite solid electrolytes can be traced back to 1984, when Latie et al. found that substituting Li for Ln and substituting Ti for Nb simultaneously in Ln 1/3 NbO 3 could result in Li x Ln 1/3 Nb 1− x Ti x O 3 , the conductivity of which is enhanced with the increase of Li content, and the activation energy is reduced by the larger bottleneck of the Li-ion channels. [ 145 ] Following the hint to maximize the low valence Ti for relatively more Li content, x can be fixed as 1, then replacing an adequate proportion of Ln can control the Li content, i.e., Li 3 x Ln 2/3− x [U + FFFF] 1/3−2 x TiO 3 (0 < x ≤ 1/6, for the vacancy density must not be less than 1). Within the years 1993–1994, Inaguma and Liquan Chen found that the bulk conductivity of Li 3 x La 2/3− x [U + FFFF] 1/3−2 x TiO 3 at ambient temperature could reach up to 10 −3 S/cm when x = 0.11, which is related to the product of Li-ion and vacancy concentrations as the rudiments of percolation model, and that Ba and Sr doping into Li-vacancy sites enlarge the bottleneck size and thus increase ionic conductivity. [ 146 , 147 ] In addition, because of the so-called lanthanide contraction, in lanthanides, increasing atomic number corresponds to decreasing atomic radius, doping with a heavier lanthanide element leads to a narrower bottleneck and lower ionic conductivity. [ 148 ] To revise the percolation model, Inaguma et al. proposed that it benefits ionic conductivity only when the Li content x is more than the threshold x c , i.e., σ ∝ ( x − x c ) μ . [ 149 ] Considering all of the foregoing, the conductivity σ of Li 3 x Ln 2/3− x [U + FFFF] 1/3−2 x TiO 3 can be expressed by a relationship among the Li content, vacancy content and that threshold [ 150 ]
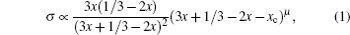
The Li-ion compounds Li 5 La 3 M 2 O 12 ( M = Ta, Nb), with garnet structure, were reported in 1988, and the structure was examined by x-ray diffraction, without knowing the Li distribution, due to limited experimental resolution of Li atoms. [ 157 ] However, this system did not attract much attention as a solid electrolyte until 2003, when Thangadurai and Weppner found that it is a good Li-ion conductor with high conductivity and a wide electrochemical window. [ 158 ] In contrast to the common perovskite or NASICON solid state electrolyte, the garnet family excludes Li-reducible Ti 4+ , so it can directly contact Li metal without damage, which has been viewed as its distinguishing advantage. [ 159 ] In 2004, Thangadurai and Weppner, together with Adams, used the bond valence sum method to verify the structure, and they minimized the mismatch of the Li-bond valence state as the isosurface to map the conduction pathways visually. It was concluded that Li ions occupy the octahedral sites other than tetrahedral vacancies. [ 160 ] The Li-ion occupation pattern is of great importance for understanding the diffusion mechanism but was not located precisely until 2006, by Cussen. It was revealed from neutron powder diffraction data that Li ions occupy both tetrahedral (80%) and octahedral sites (43%), and the latter are responsible for the mobile carriers via a clustering mechanism. [ 161 ] NMR results indicate that the Li-ion distribution depends on the annealing temperature; that is, the high annealing temperature implies that more Li ions can be quenched at the octahedral sites as mobile carriers, which leads to higher ionic conductivity. [ 162 ] In 2012, Han and Yusheng Zhao utilized variable-temperature neutron diffraction (HTND), combined with the maximum-entropy method (MEM) for data refining, to estimate the Li nuclear-density distribution and visualize the conduction pathway experimentally for the first time. These results confirm that displacement is directly driven by temperature. [ 163 ] More efforts in calculation have gradually elucidated the Li-ion diffusion mechanism; for example, conductivity and distinct mechanisms for different M elements and various Li concentrations, [ 164 ] structural phase transition, [ 165 ] concerted [ 166 , 167 ] or asynchronous phenomena, [ 168 ] point defects, [ 169 ] local structure and dynamics performance, [ 170 ] often in combination with experimental data. Other efforts focused on enhancing conductivity. Substituting and doping with lower-valence elements, e.g., replacing La by Sr [ 171 ] or Ba, [ 172 ] replacing M (= Nb, Ta) partly [ 173 ] or totally [ 174 ] by Zr, can increase Li content and thus improve conductivity. The highest conductivity found was 4× 10 −4 S/cm in Li 7 La 3 Zr 2 O 12 (LLZO), [ 174 ] the most attractive composition so far. LLZO has cubic and tetragonal phases. Cubic phase LLZO has higher conductivity and can be synthesized by doping Al or Ga, or by pulsed laser annealing. [ 175 – 179 ] Cubic phase thin film can be obtained from epitaxial growth [ 180 ] or aerosol deposition (AD). [ 181 ] The latter method prevents the electrolyte from reacting with the active electrode by avoiding the annealing process, although the obtained electrolyte exhibits extremely low conductivity (1.0× 10 −8 S/cm@140 °C) and worse cyclic performance if applied in all-solid-state batteries. Nebulized spray pyrolysis results in a thin-film hybrid of both phases. [ 182 ] The disadvantages of LLZO used in sandwich-structure all-solid-state batteries include high interface resistance and poor cyclic stability, [ 183 ] both of which can be ameliorated by introducing a thin Nb interlayer between the electrolyte and cathode (LiCoO 2 ). [ 184 ]
In 2012, a novel class of solid electrolyte, called lithium-rich anti-perovskites (LiRAP) was reported by Zhao et al. [ 185 ] LiRAP is named for the following reasons: It has a structure similar to perovskites with electronically-inverted ions located in the corresponding lattice sites. In other words, as compared with the traditional perovskite ABX 3 , X is occupied by Li + with positive charge, leading to a high concentration of Li ions (i.e., “Li rich”), A and B by halogen − (F − , Cl − , Br − , I − ) and chalcogen 2− (O 2− , S 2− ) separately with negative charges. [ 185 ] Almost at the same time, Li 3 OCl happened to be discovered as a byproduct during synthesizing Li 5 OCl 3 . [ 186 ] In the following year, phase diagram calculation results indicated that Li 3 OCl was in a less stable state (metastable phase) than Li 2 O and Li A ( A = Cl, Br) at 0 K [ 187 ] and could be stabilized by exerting a certain temperature. [ 187 , 188 ] By accommodating dopants and substitutions (e.g., halogen mixing, Li sites doped by higher-valence-state elements, and depletion of lithium halides) as well as local disorder from thermal treating process without phase transition, (anti-) perovskite has greater tolerance for structure modulation [ 189 ] to ensure structural stability and enhance conductivity. In this case, Li 3 OCl 0.5 Br 0.5 has room temperature conductivity of 6.05× 10 −3 S/cm. [ 185 ] The underlying reasons are summarized as follows: (i) With point defects, LiRAP undergoes sublattice melting at adequate temperature; [ 190 ] (ii) Concerted diffusion contributes to low activation energy; [ 187 , 190 ] (iii) Excess defects produced during synthesis process may be of critical importance for abnormally high conductivity. [ 187 , 190 ] Seen from either the original intention of materials design or the experimental and calculation results, it can be said that that higher-valence dopants and disordered state (amorphous or glassy state) account for the higher conductivity. For instance, divalent-cation doping gives amorphous LiRAP extremely high conductivity (25 mS/cm at room temperature). [ 191 ] The theoretical electrochemical window of LiRAP remains controversial, ranging from 5 eV [ 185 ] to 6.44 eV, [ 191 ] and cyclic voltammetry measurements illustrate that it can be stable up to 130 °C with 8 V applied voltage. [ 191 ] Note that despite the band gap of 5 eV, LiRAP tends to decompose into Li 2 O 2 , LiCl, and LiClO 4 under 2.5 V bias voltage. [ 187 ] The stability of Li 3 OBr when exposed to common battery solvents was investigated for many applications beyond all-solid-state LIBs. [ 192 ]
Lithium-ion inorganic solid state electrolytes have enormous advantages over traditional organic electrolytic solutions, as follows.
The performance of solid state electrolytes, such as cyclic performance, rate performance, and low temperature behavior, is always constrained by having lower conductivity than liquid electrolytes. Assuming that the voltage-drop across the electrolyte is U (mV), the current density is j (mA/cm 2 ), the thickness of the electrolyte pellet is l (cm), the conductivity can be written as: σ = ( jl )/ U (Ω −1 ·cm −1 ). The battery capacity per unit area is about 1–3 mAh/cm 2 ; thus the current density with discharge rate of 1 C is 1–3 mA/cm 2 . The area of an 18650 battery is usually about 560 cm 2 . As a result, the total battery resistance is less than 2 m·Ω, or no more than 10 m·Ω for an enterprise level battery or even at a lower level. So the inner voltage drop across a traditional battery is estimated to be about 2–10 mV, which can be used as a benchmark to evaluate all-solid-state batteries. Note that σ = (0.2∼1) × l (Ω −1 ·cm −1 ), so the solid electrolyte with conductivity of 10 −6 (Ω −1 ·cm −1 ) should have thickness of about the order of magnitude of μm (e.g., LiPON), while conductivity of 10 −3 (Ω −1 ·cm −1 ) corresponds to the thickness of mm (e.g., sandwich-structure sulfide electrolyte all-solid-state batteries). Here, only the bulk resistance is considered in the estimation, despite the possible interphase resistance, which is usually higher and can be the principal source of the full cell’s total resistance.
3. Theoretical models for characterizing the ion transport mechanism in lithium-ion solid state electrolytes
3.1. The defect and phase transition in solid state electrolytes
According to the classification given by Funke, [ 193 ] the state of totally ordered crystal is defined as level one. In this state, ions cannot leave their lattice sites, as shown in Fig.
Solid state electrolytes can be grouped into three general categories according to their defects type and phase transition mechanism, as illustrated in Fig. An evolving scheme of materials science: (a) ideally ordered crystals; (b) point disorder in crystals; (c1) crystals with structural disorder; (c2) ion-conducting glasses; (c3) polymer electrolytes; (c4) nanosized systems such as nano-composites and thin films. [ 193 ] Arrhenius plot of ionic conductivity for three types of solid state electrolytes.
Reference [ 1 ] introduced the modern transition theory established by Landau, although the nature of the parameters related to the superionic phase transition remains unclear. To theoretically explain the critical behavior, a quasi-chemical model and a lattice gas model were adopted, but neither of them is sufficient. Alternatively, the critical behavior can be understood via experimental measurements as follows: (i) conductivity and activation: the performance of critical interest and its characterization methods will be introduced in Section 4; (ii) specific heat: [ 185 , 191 , 197 – 199 ] its anomaly is one of the key indications of a phase transition; (iii) acoustic properties: the presence of an order parameter with the same symmetry as strain components results in a renormalization or softening of the elastic constant for the strain [ 200 ] or an anomaly in ultrasonic attenuation. [ 200 – 202 ] The study of these critical behaviors helps to make clear the features of order parameters and understand the interactions among ions.
3.2. Overview of the development of the theory of ionic transport in solids [ 203 – 205 ] 2 )–( 4 ), 6 ) cannot be used to characterize ion diffusion, which comprises various complications such as electric neutrality. Note that unlike solid state electrolytes with a single mobile Li + , electrode materials involve intricate non-neutral defects, especially enormous interacting vacancies when charged, and electronic conductivity cannot be ignored. As a result, what is obtained by measuring the electrode, including cyclic voltammetry (CV), [ 212 , 213 ] galvanostatic intermittent titration technique (GITT), [ 214 , 215 ] potentiostatic intermittent titration technique (PITT), [ 213 , 216 – 218 ] electrochemical impedance spectroscopy (EIS), [ 6 , 212 , 213 , 215 , 218 , 219 ] is usually about the chemical diffusion coefficient. [ 220 ] Since this review focuses on the ion diffusion in solid electrolytes, the relevant terms are only itemized here without further description. 7 ) with the same dimension as the diffusion coefficient. To build up the relationship between D σ and D *, the ratio of D * in Eq. ( 5 ) and D σ in Eq. ( 7 ) is defined as
In ordinary solids, particle diffusion is based on the Brownian motion of thermally activated defects in the periodic potential barrier. The point defect transport mechanism follows the random walk mode [ 206 – 210 ]
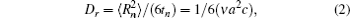
Correlation factor f can be defined as
Assuming that the lattice particles’ vibration submits to the thermal activation, the frequency can be expressed as
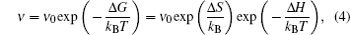
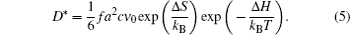
When the chemical composition varies in the diffusion zone across a certain range, a polynary diffusion couple needs to be considered. Then the diffusion particles experience various chemical environments and have different diffusion coefficients, which is usually formulated by Darken equation. [ 211 ] Taking a binary system for example:
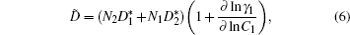
For both pure and mixed ion conductors, diffusing particles experience a drift motion in addition to random diffusion if an external voltage is applied as the driving force. So the relationship between the ionic DC conductivity σ dc and the diffusion coefficient D σ can be written according to the Nernst–Einstein equation as
The limitation of random walk theory lies in the requirement that the ionic transport should not be affected by other accompanying defects, which seems hard to satisfy in solid state electrolytes with their relatively high conductivity. This is because of the following: (i) In the static energy landscape for most solid state electrolytes, the energy valley sites (equivalent positions for mobile ions) are more numerous than the actually occupied sites (the number of mobile ions in fact). [ 1 , 9 ] The maximum of the equivalent sites leads to the sketch of sublattice melting, of which the mobile ions can diffuse “freely” like liquid. (ii) Concerted ion migration always leads to lower activation energy because the energy landscape is dynamic instead of static. In a sketch of dynamics, time scale is of critical importance. [ 1 , 9 , 195 ]
3.3. Four theoretical models for characterizing diffusion in solids [ 1 , 9 , 222 ]
3.3.1. Two-state model [ 1 , 223 ] 10 ) in the direct space can be transformed to Fourier space as 
k ,− t ) = P ( k , t ), the frequency domain solution is k ) can be measured by a quasielastic Mossbauer spectrum and quasielastic neutron scattering, as will be illustrated in Section 4.3.2. Then the diffusion coefficient can be derived from Λ ( k ) as k , t ) in complicated cases. [ 224 ] One of the underlying reasons is that the potential barrier and potential well can vary within a certain energy range in the disordered structure. [ 224 – 227 ] Figure 5 shows the common complicated models, in which Γ fi ((f)-final, (i)-initial) is the hopping rate resulting from random lattice potential. ![]()
![]()
![]()
The ion diffusion process in a fixed lattice’s energy landscape can be simplified and viewed as a two-state model, i.e., a bound state and an approximately free-ion state, and an energy barrier exists between them depending on an effect of the static skeleton lattices. Once an ion has energy above the barrier threshold, it can be excited from the bound state to the approximately free-ion state with a certain life time and can transport with the velocity of free ions. This model can be characterized with several different mathematical formulations. Herein, by introducing the conditional probability P (
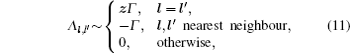
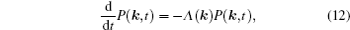
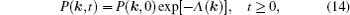
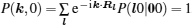
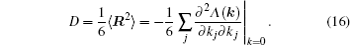
As mentioned in the dynamics sketch, for solid state electrolytes, the release time τ r is not infinitely short and the trapping time τ t is not infinitely long. In two-state model, the conditional probability can be divided into the free part and trapped part as
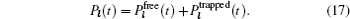
Models of disordered potential barriers and wells. [ 223 ] (a) RB, (b) RT, (c) RB+RT, and (d) RBS.
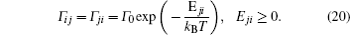
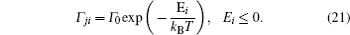
A special case of the percolation model indicates the condition that the lattice sites are randomly blocked and cannot accept the hopping ions,
3.3.2. Lattice gas model [ 1 , 223 ] l ′ is occupied ( l ′) and site l is empty ( l̄ ) at time t . By taking into account 9 ), and can be solved analogically. The collective diffusion coefficient is D coll = Γ a 2 . Note that the site-exclusion lattice gas concentration is not included in Eq. ( 26 ). r l and r λ represent the displacements of A and B relative to the equilibrium position, respectively; the potential φ includes interactions among all particles. When φ is expanded with respect to displacements 
r a to 
40 )–( 43 ) for some special cases can be found in Ref. [ 1 ]. The Monte Carlo (MC) simulation details of the diffusion process are presented in Ref. [ 230 ].
In this model, the crystal volume is divided into a substantial number of units; each unit can be occupied by no more than one particle. Comparison between the lattice gas model and the two-state model suggests that the latter indicates single-particle transport along the energy landscape; whereas the former indicates many-particle diffusion, in which the interaction among mobile particles is introduced by assuming unit exclusion.
In the case of ordered structure, particles can hop into the nearest-neighbor non-blocked sites at a constant rate Γ . This model was introduced by Spitzer, [ 228 ] and the exact results can be found in Ref. [ 229 ]. The master equation is
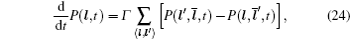
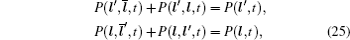
In the case of disordered structure, the space correlation occurs; thus even the simplified site-exclusion model is complicated. Some solutions of specific cases can be found in Ref. [ 223 ]. Three common models are listed as follows (here an energy ɛ i is assigned to each lattice site i ).
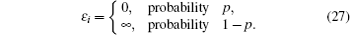
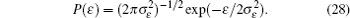
Interactions among mobile particles can be introduced as follows: (i) For an ordered structure, the average of all interactions can be simplified by a mean field approximation. (ii) For a disordered structure, the interaction among particles is too complicated to describe exactly. We deal with this by assuming that the solid state electrolyte consists of merely two kind of ions: skeleton ions A and mobile ions B . Then the Hamilton equation of the lattice gas model can be constructed as follows: [ 1 ]
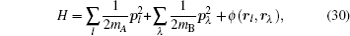
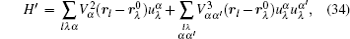
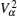
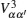
Let us consider an N -particle system with charges e n and masses m n , n = 1, 2, …, N . Periodic lattice sites are defined by the position vector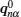 
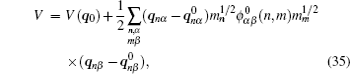
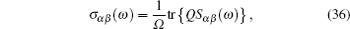
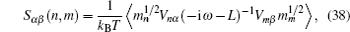
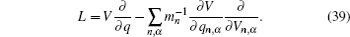
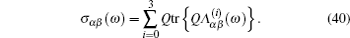
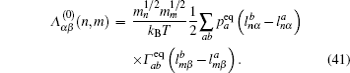
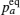
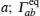
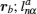
The free-ion model of the ordered structure is a single-particle approximation, which results in a typical linear Arrhenius plot with a constant slope, and the behavior of solid state electrolytes are unrelated to the frequency. If we take the free-ion model to analyze the frequency-dependent experimental results and the nonlinear Arrhenius plot for the ionic conductivity, they can be ascribed to the disorder of crystal structure and the Coulomb interaction. Given that only the disorder of crystal structure is involved in the free-ion model, some phenomenological and semi-microscopic approaches have been developed to explain the frequency dependent results. Nevertheless, many experimental phenomena remain that cannot be explained quantitatively. [ 231 – 234 ]
Compared with the free-ion model, the lattice gas model maps the interactions among the many bodies onto the dynamics of a single particle moving in a complex energy landscape. Through the theoretical calculations, the disordered structure and Coulomb interaction can conveniently be taken into consideration to simulate and fit the experimental results, including the nearly constant loss (NCL) in the high frequency region, the quasielastic scattering and NMR. Besides, the literature on fitting the Arrhenius plot with the lattice gas model indicates that low temperature conductivity is affected by both lattice disorder and Coulomb interaction, whereas the high temperature behavior is influenced by Coulomb interaction only, resulting in lower activation energy. [ 230 ]
3.3.3. Continuous stochastic model [ 1 , 230 ] 
r , t ). Note that there exists the frequency threshold ω NCL , and that when ω > ω NCL , Re 
Q , ω ) is determined by the coherent and incoherent correlation functions G ( r , t ) and G S ( r , t ), the correlation functions cannot be obtained from S tot ( Q , ω ) conversely. This is because the correlation functions contain more information than S tot ( Q , ω ). As a result, it is hard to identify the ionic diffusion mechanism from the dynamic structure factor deviation, without making other assumptions. 
In order to describe the complicated multi-particle dynamics, the system can be simplified as an effective single-particle dynamics model, called continuous stochastic model, as shown in Fig. Ionic motion in flat potential with potential barriers V 0 (adapted from Ref. [ 1 ]).
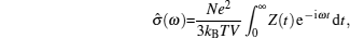
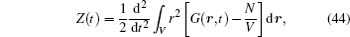
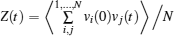
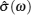
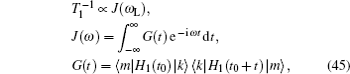
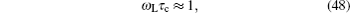
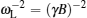
The coherent and incoherent dynamic structure factors of the mobile ions are given by
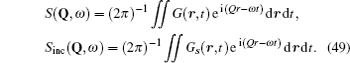
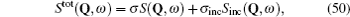
Although the continuous stochastic model was phenomenological at first, [ 240 , 241 ] it can be microscopically obtained from the Hamiltonian. [ 242 ] Assume that mobile ions move continuously in the skeleton potential V 0 , which is driven by the system forces based on the displacement relative to the equilibrium sites of mobile ions. The system’s potential is strongly inharmonic when applied the disordered structure or Coulomb interaction, and valleys control oscillation, while barriers control diffusion. The skeleton vibrations ( H B ) are treated as a bath, and the coupling term H ′ provides the random forces and friction. The interaction among the mobile ions is indirectly considered by being integrated into the bath so that the simplified solution can be written as the Langevin equation. Take one-dimensional motion for example
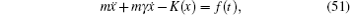
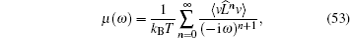
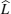
To sum up, theoretically speaking, ion diffusion in a solid state electrolyte is a complicated process. The above methods can give the analytic solutions only under extremely simplified conditions. In order to investigate the ion diffusion in solid state electrolytes quantitatively, one needs to adopt the atomic-scale molecular dynamics [ 253 – 255 ] and semi micro-Monte Carlo simulations. [ 230 , 238 , 256 – 260 ]
3.3.4. Percolation model [ 261 ] ![]()
![]()
![]()
The models in Sections 3.3.1–3.3.3 focus mainly on the micro-diffusion, or the macro-effects derived from the micromechanism. In contrast, the percolation model concentrates more on the macro-diffusion mechanism and is often used to describe the amorphous states (organic polymers, inorganic glasses), composite conductors and porous media.
The site-percolation model is usually used to describe inorganic crystals with sites occupied randomly. A sketch of it is shown in Fig. Site percolation on a square lattice: The small circles represent the occupied sites for three different concentrations: p = 0.2, 0.59, and 0.80. Nearest-neighbor cluster sites are connected by lines representing the bonds. Filled circles are used for finite clusters, while open circles mark the large infinite clusters. [ 261 ] (a) p = 0.2, (b) p = 0.59, (c) p = 0.8.
Bond percolation model is illustrated in Fig. (a) Bond percolation cluster on a square lattice and (b) continuum percolation of conductive material with circular holes of fixed radius at the percolation threshold. [ 261 ]
If two components of a random mixture are not restricted at the discrete sites in a regular lattice but are continuously distributed, as shown in Fig.
Only solid–solid composite electrolytes are within the scope of this review. The attention paid to this family can be traced back to 1973, when Liang found an abnormal enhancement of conductivity by dispersing Al 2 O 3 particles into a LiI matrix. [ 42 ] The space-charge layer theory was developed to explain this phenomenon. [ 266 – 270 ] It assumes a high concentration of interlayer defects between the insulated and conductive phases. As a result, composite electrolytes are considered to be three-phase systems with the conductivity phase A , insulator phase B , and interphase C , among which C has very high conductivity because of the substantial frequency of defects. Figure 
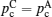
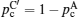
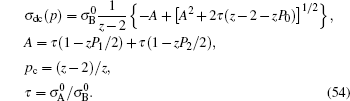
Illustration of the three-component percolation model for dispersed ionic conductors, for different concentrations p of the insulating material. The insulator is represented by the grey area, the ionic conductor by the white area. The bonds can be highly conducting bonds (A bonds, bold lines), normal conducting bonds(B bonds, thin lines), or insulating (C bonds, dashed lines). (a)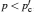 
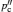
4. Experimental methods for characterizing ion transport mechanism in lithium-ion solid state electrolytes
In order to provide insight into the microscopic kinetic process, absorption, reflection and scattering techniques are often used to investigate the interaction of electromagnetic waves or probe particles with matter, as shown in Table Frequency ranges of phenomena and methods used to study solid state electrolytes. [ 9 ] Map of dynamical modes (from the lecture of 2013 Oxford School on Neutron Scattering, drawn by Victoria Garcia Sakai). [ 276 ] Name of radiation λ −1 /cm −1 λ Frequency/Hz Phenomena and methods 3 Å 10 18 X-ray 30 Å 10 17 photon interaction Ultraviolet 300 Å 10 16 3000 Å 10 15 Visible light 3 μm 10 14 Infrared 1000 30 μm 10 13 ion vibration 100 300 μm 10 12 Fourier spectroscopy Far infrared 10 10 11 neutron scattering 1 10 10 40 GHz light scattering Microwave 30 cm 10 9 2 GHz (Raman, Brillouin) 3 m 10 8 acoustic phonons Radio shortwave 30m 10 7 medium 300 m 10 6 1 MHz longwave 3000 m 10 5 10 4 10 3 1 kHz AC impedance 10 2 measurements Alternating current (AC) 10 1 10 −1 electrode diffusion 10 −2 phenomena 10 −3 1 mHz H L Direct current (DC) 10 -∞ DC measurements
4.1. Crystal structure and lithium-ion occupation pattern
Since many topics of solid state electrolytes are rooted in the crystal structure, as shown in Section 2, e.g., skeletons and mobile ion sublattices, disordered structure resulting from the superionic phase transition and Li-ion displacement arising from phonon mode softening, x-ray diffraction (XRD) is the method of choice to determine the crystal structure; its mechanism is shown in Fig.
4.2. Lithium-ion conduction pathways
For the superionic conductors, the relaxation time, when ions leave lattice sites and transport across barriers, cannot be ignored. Driven by the temperature, Li ions arrange themselves statistically in an ellipsoid shape around the lattice sites and have opportunities to connect as a pathway at higher temperatures. With the help of high-temperature neutron diffraction (HTND) and the maximum-entropy method (MEM), the Li nuclear-density distribution and even the conduction pathway can be estimated, which was first used by Yamada et al. to study LiFePO 4 [ 278 ] and then solid state electrolytes [ 140 , 161 ] as well. XRD, ND, and ND+MEM are always combined to obtain the information about the structure and diffusion mechanism more and more accurately. Taking garnet as an example, the skeleton lattice is initially determined by XRD, [ 157 ] then powder ND is applied to confirm the Li ion positions exactly, as very important structure information, [ 161 ] and HTND with MEM is subsequently used to map the conduction pathway. [ 163 ] Left: interaction of matter with (a) x-rays and (b) neutrons. (c) Mass attenuation coefficients for thermal neutrons and 100 keV x-rays for the elements (natural isotopical mixture unless stated differently). [ 277 ]
4.3. Lithium-ion conductivity and diffusion coefficient
Methods for measuring the diffusion coefficient can be grouped into two major categories: direct methods based on Fick’s laws, and indirect methods not based directly on Fick’s laws. As illustrated in Section 3, macroscopic and microscopic diffusion mechanisms are not always consistent with each other, and can be transformed to each other with the correlation factor. Table
4.3.1. Direct methods [ 280 ]
The tracer method is the most direct and accurate technique to determine the (self- or impurity) diffusion coefficient in solids. Since the number of tagged atoms is very small, tracer isotopes will not influence the chemical composition. The isotope can be either radioactive or stable. The best way to determine the concentration-depth profile is to serial-section the sample and then measure the amount of tracer per section. If the diffusion coefficient is very small and the diffusion depth is less than 1 μm, it is hard to section and determine the tracer amount exactly. In addition, several other profiling and detection methods are commonly employed, including secondary ion mass spectrometry (SIMS), electron microprobe analysis (EMPA), Auger electron spectroscopy (AES), Rutherford backscattering spectrometry (RBS), nuclear reaction analysis (NRA), and field gradient nuclear magnetic resonance ((P)FG NMR), [ 281 ] details of which can be found Ref. [ 278 ] and references identified therein. Typical ranges of the diffusivity D and motional correlation time τ c of some macroscopic and microscopic methods. FG-NMR: field gradient NMR, β -NMR: β -radiation-detected NMR, QENS: quasielastic neutron scattering, MS: Mössbauer spectroscopy. The hatched bar indicates the transition from solid to liquid, wherein the motional correlation time is reduced by about two orders of magnitude (adapted from Ref. [ 204 ]).
4.3.2. Indirect methods
As shown in Eq. (8), the self-diffusion coefficient D * can be determined by D σ derived from the electrical conductivity and Haven ratio H R . [ 204 ] Note that for the electrode, the problem is more complicated, with the chemical potential, concentration and cross ionic/electronic phenomenological coefficients. [ 279 ]
AC impedance spectroscopy is the most common technique for determining conductivity. It can identify the contributions of bulk and grain boundary especially for polycrystalline, and make it possible to investigate how the microstructure affects the overall conductivity. [ 282 ] The principle is as follows: apply an AC voltage U ( ω ) = U 0 e i ωt to the sample, and the responding current is I ( ω ) = I 0 e i ( ωt + Φ ) with the same frequency as the voltage but a phase shift Φ . As a result, the complex impedance with a real part indicating conductivity and an imaginary part indicating capacity is defined by Ohm’s law: Z ( ω ) = U ( ω )/ I ( ω ) = Z 0 e −iΦ = Z 0 cos Φ − i Z 0 sin Φ , and can be fitted from the equivalent circuit to give the microstructure information. [ 204 ]
In addition, by adding a microelectrode or nanoelectrode, the local conductivity of each local point within the bulk and grain boundary can be mapped in spatial scale. [ 283 – 286 ] More specifically, one method is to cover the surface of objects with micro-electrodes, as shown in Fig. (a) Polycrystalline SrTiO 3 with microelectrodes on the top in the optical microscope, (b) the orientations of the grains, (c) microelectrode, (d) sketch of a model sample, (e) image of circular microelectrodes contacted by tips. [ 283 ] Schematic drawing of the nanoelectrode setup. [ 284 ]
The Hall effect is employed as an alternative method to study conduction behavior. [ 287 – 290 ] Note that this method is suitable to Ag ionic conductors, which have high ionic conductivity and are typical examples of the sublattice melting model. However, as far as we are concerned, the relationship between Hall mobility and conductivity mobility remains unclear. This is because the Hall effect is understood in terms of the quasiliquid model, which is not really true for most ionic conductors. Especially for Li-ion solid electrolytes, the complicated long-range interactions, including those among mobile ions and those between mobile ions and skeleton lattices, can lead to larger deviations.
Mechanical relaxation methods are possible because atomic motion in a material can be induced by an external disturbance like applied mechanical stress, either constant or oscillating. In ferromagnetic materials, the interaction between the magnetic moments and local order can give rise to various relaxation phenomena similar to those observed in anelasticity. They are rarely applied to the study of solid electrolytes.
Nuclear methods include nuclear magnetic resonance (NMR), [ 281 , 292 , 293 ] quasielastic Mössbauer spectroscopy (MBS), [ 294 ] and quasielastic neutron scattering (QENS). [ 280 , 295 ]
NMR is a powerful tool for studying materials. It can probe both the short range and long range motions, and can identify atoms located on inequivalent sites. There are various kinds of NMR, among which FG NMR is usually applied to investigate particle diffusion and particles’ interaction with structure in mesoporous medium, [ 281 ] and also can be used to measure the long-range correlation in Li-ion solid state electrolytes with response time scale on the order of milliseconds. [ 138 , 296 ] On the other hand, electrophoretic NMR is usually used to study the charged particles in liquid. [ 293 ] Beyond such macroscopic applications, the diffusion process can be investigated by NMR for atomistic time scales, i.e., transient studies and wideline studies.
In transient studies, the sample in a static external magnetic field is exposed to a brief, intense pulse of radio-frequency radiation. This pulse transfers additional energy to nuclei, which leads to a phase correlation of nuclei normal motion in the external magnetic field. Removal of the pulse means that nuclei transfer energy to the surrounding environment, and the phase correlation decays in two characteristic times (spin-lattice relaxation time T 1 and spin–spin relaxation time T 2 ). The magnitudes of T 1 and T 2 reflect the interaction strength between the nuclei and their environment. The extended methods of transient studies make use of the spinlattice relaxation in the rotating frame, with the characteristic time T 1 ρ , whose property is between T 1 and T 2 , as shown in Fig. Schematic of the relaxation rates, 
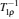
In the wideline studies, the sample is exposed to a static external magnetic field and a continuously applied, small radio frequency field. Then the position, width, and shape of the absorption spectrum reflects the interaction between nuclei and their microscopic local surroundings, such as the magnetic moments of adjacent nuclei, electric field gradients, and other components of the compound (e.g., paramagnetic electronic species and conduction electrons). As for the superionic phase, mobile carriers can move “freely” across the skeleton, which leads to the average uniformity of local field everywhere. As a result, 
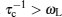
Compared to “elastic” methods, “quasielastic” methods indicate a small amount of transference of energy, which enables the measurement to probe the dynamic characteristic of elements. Quasielastic neutron scattering (QENS) and uasielastic Mössbauer spectroscopy (QEMS) are common quasielastic techniques, the principle of which has been introduced in Section 3.3.3, presenting the proportional relationship between the spectrum intensity and dynamic structure factor S tot ( Simplified, semiclassical explanation of diffusional line broadening for QEMS (a) and QENS (b). [ 294 ]
4.4. Complete conductivity spectra [ 9 , 194 ]
As shown in Table Schematic overview of different techniques for the measurement of frequency-dependent conductivity. [ 194 ] Schematic comparison of the current density autocorrelation function and the conductivity dispersion in (a) crystals with thermal activating defects, (b) a dilute strong liquid electrolyte, and (c) a structurally disordered solid electrolyte. [ 194 ] (d) The jump relaxation model. [ 299 ]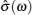 
A schematic of complete conductivity spectra of various systems is shown in Figs. Sketch of a set of frequency-dependent conductivity isotherms (Adapted from Refs. [ 194 ] and [ 299 ]).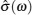 
Figure
5. Factors influencing the ionic conductivity in lithium-ion solid state electrolytes
Seeing from the development history of solid state electrolytes as reviewed above, the conductivities of various conductor families span a wide range, and only a handful of them can attain high enough conductivity, usually with the open structure, which can be regarded as the critical factor leading to the superionic conductors. However, it is still not clear how to evaluate the structure quantitatively, and what is the consequent correlation between the specific structure and the high conductivity. In order to investigate the relationship between structure and performance, the method of high-throughput calculations was developed specially for Li-ion solid state electrolytes. [ 82 , 300 ] Much more work is in process on effective data mining. [ 301 ]
For enhancing the performance of the known solid state electrolytes, efforts are usually focused on higher carrier concentration, more sites suitable for Li-ion occupation, and the connective conduction pathway caused by the former two aspects meeting the requirement of the percolation model. Figure Besides varying simple state parameters, such as pressure and temperature (electric field, etc.), the variation of morphological complexity evolves, in addition to the well-known strategy of varying chemical complexity, to a more powerful method in materials engineering. [ 302 ]
From the compositional aspect, doping and substituting by elements with different valence states, concerning the knowledge of defect chemistry, is one of the most common and effective ways to enhance the conductivity of solid state electrolytes. Besides, the structural parameters can usually be finely tuned by dopants and substitutions with different ionic radius within the concentration range of solid solution, and the parameters, or the size of the “bottleneck” in the Li-ion conduction pathway, can be optimized to the certain values for higher conductivity. In addition, the element types of dopants and substitutions located at the skeleton sites have the different interaction with mobile Li ions, and weaker interaction usually enables Li ions to transport more freely.
From the morphological aspect, other effective methods to increase the ionic conductivity are applying glass state or glass-ceramic state instead of crystalline state, as well applying composite materials. Moreover, in all-solid-state batteries’ applications, there exists the interphase problem derived from matching the electrolytes and electrodes (both cathodes and anodes, and the latter are usually referred to as SEI, i.e., solid electrolyte interphase), leading to the striking high resistance, which can even become the most severe limitation of the full cell’s conductivity. As a result, decreasing, or even eliminating the interphase resistance, will enhance the full cell performance effectively.
5.1. Structural disorder 55 ) reduces to the normal Arrhenius equation. This equation can be explained by a configurational entropy theory, [ 305 ] or a free-volume theory. [ 306 , 307 ] In the configurational entropy theory, the transition state is supposed to form by the correlational fluctuation of atomic (or ionic) configuration; the configurational entropy reads: S C ∼ Δ C p / T +const, and the transition probability per unit time can be written as 
55 ) can be obtained. In the free-volume theory, molecular transport occurs only when the voids having a volume V greater than some critical volume V *, and the free volumes distribute randomly in liquid. Then the temperature dependence of the average free volume V f is approximately V f = V 0 α f ( T − T 0 ), where α f is the thermal expansion coefficient of the free volume in the liquid state; T 0 is the temperature at which the free volume vanishes and V 0 is the volume of the liquid at T 0 . Therefore, the diffusion coefficient is written as D = D 0 ( γ V */ V f ), which can also be reorganized to Eq. ( 55 ). When the barrier potential effect is considered, [ 308 ] only atoms with energy higher than the barrier potential E V can hop out of the local equilibrium sites effectively, and thus the diffusion coefficient can be rewritten as D = D 0 [−( γV */ V f ) + ( E V / kT )], which can be used to fit the Arrhenius plot of polymers [ 309 , 310 ] and glasses [ 311 , 312 ] well. All above efforts are attempting to fit the experimental curve, and by revising the diffusion coefficient equation, the mechanism causing the deviation is supposed. In fact, the transport mechanism differs greatly in different materials. Taking Li-ion solid state electrolytes as an example, of the inorganic glasses the Li ions’ mobility usually approaches 1 while the mobility of the polymers is much less than 1 for both cation and anion transport. The greater difference lies in the ion hopping mechanism: for the disordered inorganic solid, the motion can be explained by the lattice gas model or continuous stochastic model presented in Section 3.3; for the polymers, the ionic motion is mediated by the peristalsis of segments and fluctuation of skeleton ions, which provide the ions conduction pathway randomly. Moynihan and Angell identified the different transport mechanisms between polymers and glasses by using the concepts of “coupled” and “decoupled”, [ 313 – 317 ] and explain successfully why the inorganic solid state electrolytes can work under the glass transition temperature T g .
The development history of glass and polymer and ionic transport are reviewed in detail in Ref. [ 303 ]. The structure characterization techniques of amorphous solid electrolytes are similar to those of crystal electrolytes, with the emphasis placed on the short-range and medium-range order, which is of critical importance for Li-ion diffusion in the amorphous state. [ 304 ] Ionic conduction is the process that the locally (at atomic scale) ordered lattice ions are excited to the disordered neighboring sites, then collectively diffuse in macroscopic scale. That is, the disorder and the collective motion are the key points with the following relationship: the correlation of independent point defects is weak, while for the amorphous materials with abundant defects, the interaction cannot be neglected among mobile ions and even among mobile ions and skeleton ions. The experimental techniques for studying amorphous ionic conductors are shown in Fig. Space-time hierarchy structure of amorphous ionic conductor experimental techniques (The original image is from Ref. [ 303 ], and the daptation is from Prof. Kawamura Junichi’s private mail).
For the crystal with ordered structure, the ionic conductivity is often expressed by Arrhenius type law as: σ DC T = A σ exp (− E σ / k B T ). However, for the disordered glasses and polymers, and even some crystalline solid state electrolytes with Li ions and “vacancies” randomly occupied, the conductivity expression will deviate from the typical Arrhenius type (i.e., the relationship between the logarithm of conductivity and the inverse of temperature deviates from linear), and the consequent examples with curved Arrhenius relationships are shown in Figs.
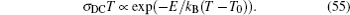
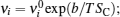
The present review concentrates on the discussion of inorganic solid state electrolytes. At the time scale of mobile carrier diffusion, the crystal skeleton is supposed to be highly stable, while the interaction between skeleton and mobile ions cannot be ignored. [ 239 ] As compared with Eq. (
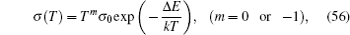
In order to explain the experimental results, some phenomenological and semi-microscopic methods have beenthe introduced, including lattice gas model mentioned above, coupling scheme proposed by Ngai et al. , [ 231 ] the jump relaxation model proposed by Funke, [ 299 ] the diffusion-controlled relaxation model proposed by Elliott and Owens, [ 234 ] and so on. Besides the above theoretical models, numerical simulation methods such as MD and MC also play important roles.
Although no final conclusion for ion diffusion in disordered structures can be theoretically drawn, and the experimental results can usually be explained only phenomenologically, experiments do indicate that amorphous materials of certain systems show higher conductivity. The increase of conductivity may result from the substantial defects for the inorganic glasses or may be attributed to a means of fabrication of glasses that is good for eliminating pores and suspending grain boundaries. In addition, during the process of glass preparation, because of the freezing of thermal fluctuation, the heterogeneous structures form intrinsically. [ 321 – 323 ] Moreover, when the crystalline materials mix into, or segregate from glass basement, the conductivity of product is further enhanced, which may arise from the enrichment of defects surrounding the crystalline materials or to the heterogeneity effect introduced below in composite materials. In this case, the percolation model must be taken into consideration for the ion diffusion, not only in homogeneity, but also with the preference in certain regions. [ 230 , 261 , 324 ]
5.2. Composite materials
As shown in Fig. Qualitative sketch of the two-phase anomaly of effective composite conductivity and storage capacity based on redistribution processes (contact equilibrium) at the interfaces. Strictly speaking, percolation effects lead to modification in the shape for the transport case. [ 302 ] Examples of ionic space charge effects at various contacts. Introduction of (a) Al 2 O 3 and (b) SiO 2 particles into (a) AgCl (b) CaF 2 , leading to vacancy enriched regions that provide highly conductive pathways; (c) addition of alkaline Al 2 O 3 to metal Ag, leading to the an adsorption of Ag + resulting in vacancy enriched regions, and enhancing Ag + conductivity which can compete with e − conductivity; (d) addition of acidic SiO 2 to Li-salt containing polymers or liquids, leading to an adsorption of the anions resulting in breaking ion pairs and enhancing Li + conductivity; (e) the simple grain boundaries in AgCl, adsorbing Ag + and increasing the silver vacancy concentration in the vicinity; (f) the simple grain boundaries in CeO 2 , where electrons accumulated, inverting the O 2− conductivity invert to n-type conductivity; additions of (g) NH 3 and (h) BF 3 as (g) Ag + and (h) F − attractors, resulting in the contamination of the grain boundaries to accumulate the mobile carries such as (g) Ag + and (h) F − respectively; the inhomogeneous grain boundary between (i) AgCl and β -AgI, (j) CaF 2 and BaF 2 , and (k) M (metal) and MX, accumulating Ag + , F − , and M + respectively; (l) the inhomogeneous grain boundary between LiX and M (metal), where Li + accumulated at LiX side while e − at M side, leading to the mixed electronic–ionic conductor at interfaces; (m) addition of MX particles into M + X − aqueous solution, leading to an adsorption of (M + X − ) aq ; (n) addition Pt as the catalyzer to accumulate O 2− at the surface; MX with the (o) two-dimensional and (p) zero-dimensional (point contacting) homogeneous interphase MX, adsorbing M + (o) at interphase and (p) host matrix respectively. [ 325 ]
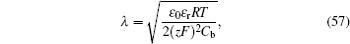
For the materials controlled by interface, the interphase region can be enlarged by diminishing the particle size, which belongs to Nanoionics theory. Maier proposes that the size effects are classified into two kinds as shown in Fig. Explicit and implicit size dependence of resistive and capacitive elements that are required to describe (electro) chemical transport or storage. [ 302 ] Size effects classified according to their contribution to the total chemical potential. [ 331 ]
In addition to the charge carriers redistribution at the grain boundaries, another important influence on concentration variations is the formation (free) energy, or more precisely speaking, the standard chemical potentials. The two aspects above are not independent, for the formation of grain boundaries is often ascribed to the defects relaxation induced by (electro) chemistry. By considering the macroscopic and microscopic effects related to the size comprehensively, size effects can be classified according to their contribution to the total chemical potential, as shown in Fig.
Note that there is no clear distinction between disordered and composite materials, because the former can be regarded as the limit of the latter, when all atoms have lost the longrange order and the whole macroscopic system consists only of grain boundaries. As a result, the percolation model must be considered in various space scales to account for the different degrees of mixing from atomistic to mesoscopic to macroscopic levels, corresponding to glass to polycrystalline/glassceramic to classic mixture with the miscibility gap.
5.3. Interphase between solid state electrolyte and electrode
In considering the solid electrolytes in contact with the electrode materials, the critical problem lies in the interface with usually small, and even point contact area. For the thin film batteries fabricated by RF sputtering, via the strict control of preparation process, the layers of electrolyte and electrode can be dense and basically free of grain boundaries and are in close contact with each other at atomic scale. For all-solid-state batteries with the sandwich structure, if oxides are provided as solid state electrolytes, the electrodes should be fabricated by mixing electrolyte materials into electrode materials. Then the primitive loose mixture with sandwich structure is sintered to enlarge the contact area and eliminate the interface resistance. In contrast, since sulfides have good ductility, with Yong’s modulus between polymers and oxide ceramics, [ 332 , 333 ] their grain boundary resistance can be reduced only by the cold pressing, [ 332 – 334 ] and they can contact with other materials (including electrodes and the other compositions in composite electrolytes) closely. [ 335 ] Another method to improve the physical contact of solid–solid phases is to modulate the materials’ morphology. [ 336 ] When Li metal or Li–In alloy is applied as the anode, because of the good ductility of metal, the physical contact is no longer the most critical problem, but is replaced by the preferential consideration of chemical stability, electrochemical stability and space charge layer.
5.3.1. Solid state electrolyte/anode interphase and mixing transport
The solid state electrolytes are electronic insulator with the Li-ion mobility as 1, although at the interface with electrodes, the complicated ionic–electronic mixed conductivity occurs as the result of electron tunneling or (electro)chemical reaction. This effect is especially significant when the solid state electrolyte is in contact with the anode.
Carbon as anode and organic electrolytic solution as electrolyte are usually applied in Li-ion batteries these days, and the formation of SEI (solid electrolyte interphase) film on the surface of carbon anodes contribute mostly to their application. SEI film grows at the cost of capacity loss, and restricts rate performance; as a result, it is expected that SEI film can be stable and compact after the initial charge–discharge cycle, to prevent electrons from penetrating into organic electrolytic solution to promote the decomposition of electrolyte accompanied by the growth of SEI film. Investigated by ab initio calculations of the microscopic mechanism of the formation of SEI film, the rate of electron tunneling is obtained, indicating that in the nonadiabatic regime the reorganization of solvent molecules can slow the electron transfer. [ 337 ] The makeup of this film is so complicated [ 338 ] that the Li-ion transport mechanism within it is hard to study. Li 2 CO 3 as the principal inorganic constituent has extremely low conductivity [ 2 – 5 ] and is not at all a “superionic conductor”. The Li-ion transport mechanism is studied by calculation, [ 4 , 5 , 339 , 340 ] ascribing the conductivity to the interstitial Li ions hopping by means of “knock-off”. [ 4 , 5 , 339 ] However, Li can diffuse in the form of atoms, [ 4 ] concerning the electronic–ionic mixed transport, and resulting in the continuous growth of SEI film.
It is generally accepted that one of the advantages of inorganic solid electrolytes lies in their probable wide electrochemical window, because it would prohibit the formation of SEI film. However, this conclusion was questioned by a recent study. By applying electron energy loss spectroscopy (EELS) combined with scanning transmission electron microscopy (STEM) to investigate a solid state battery with LIPON as the electrolyte, an interface layer can be obviously observed between LiPON and Si anode. Note that as compared with energy dispersive x-ray (EDX), EELS has a higher resolution for light elements such as Li, which is an advantage for investigating Li-ion batteries, as shown in Fig. Spatially resolved electron energy-loss spectroscopy in transmission electron microscopy mode (SR-TEM-EELS). [ 341 ]
Among the oxide solid state electrolytes, the perovskite and NASICON families usually have high conductivity. However, the compositions with highest conductivity of both of them contain Ti with variable valence which can be reduced. Moreover, the Li intercalation reaction is experimentally confirmed. [ 343 , 344 ] Therefore, when NASICON is used as solid state electrolyte, Li anode can be precipitated in situ opposite the cathode side by the first cycle charging, as shown in Fig. Cross-sectional image of the Si/interphase/LIPON by (a) SEM and (b) EELS. [ 342 ] Li concentration profile and its effects on Ti and O. (a) One-dimensional Li concentration profile with Ti 4+ and Ti 3+ regions; (b) profile of average O–O distance; (c) spectra of Ti L − edge , showing the Ti 3+ and Ti 4+ features; (d) spectra of O- K -edge, both peaks “a” and “b” are shifted by the Li insertion in the negative electrode. [ 341 ]
Some sulfide solid state electrolytes, especially those containing Ge (e.g., glass-ceramics with Ge [ 345 ] and crystalline Li 10 GeP 2 S 12 [ 132 ] ) or Si, [ 100 , 345 , 346 ] whose reduction potentials are higher than Ti 4+ , can even react with graphite anode.
In conclusion, the solid state electrolytes must be selected by their electrochemical windows according to the electrode materials, or different electrolytes are selected for either-side contact with anodes and electrodes, to satisfy the requirement of prohibiting reduction at the anode as well as oxidization at the cathode side. [ 100 , 132 , 345 ]
5.3.2. Solid state electrolyte/cathode interphase and space charge layer
Owing to the development of sulfide solid electrolytes, the problem related to the grain boundary is basically solved, and conductivity is no longer the restriction. At present, the greater challenge is about the interface, including: the mutual diffusion caused by the different electronegativity at either side of interface, the uncertainty of interphase structure arising from the crystal lattice mismatch, the thermal activating point/line/plane defects (including space charge layer). [ 348 ] In addition, at the time scale, the dynamic process that charge and mass transfer during the charging–discharging will result in the new problems, and at the space scale, the interface with thickness of nanometers results in “small size effect”, which is categorized into nanoionics. [ 325 , 331 ] All mentioned above add the difficulty to the experiments and calculations.
As was first proposed by Takada research group, [ 349 ] it is the interface between the solid electrolyte and cathode, rather than the electrolyte itself that limits the high rate performance of sulfide solid electrolytes with high conductivity, and the mechanism is shown in Fig. Schematic of the reduction mechanism of electrode resistance at a 4 V cathode/sulfide electrolyte interface. [ 347 ] (a) Preparation of the solid-state lithium battery, left: schematic illustration of the sample, and right: TEM image around the LATSPO/Pt interface; (b) macroscopic measurement of the battery reaction, left: initial Li-insertion/extraction reaction of the LATSPO/Pt half-cell at 3.0–1.5 V (versus Li/Li + ), I = 5 μA (electrode area: 0.785 cm 2 ), and right: initial cyclic volt ammogram (40 mV·min −1 ) measured in the TEM. (c) Electric potential distribution during the initial CV measurement. Panels (c1)–(c7) in the right indicate the distributions on the negative side along the line “A–B” in panel (a). The applied voltages between the current collectors correspond to the points c1–c7 indicated in the right of panel (b). Potential ( V ) is given on the vertical axis. [ 354 ]
6. Conclusion and outlook
6.1. Material systems
At present, the material systems related to Li-ion conductors are finite. A number of them have relatively high conductivity, and even reach up to that of electrolytic solution, as shown in Figs.
As for the application of solid state electrolytes in all-solid-state batteries, the film batteries with LiPON as electrolyte have good cycling performance, [ 6 , 92 ] although it is costly to scale up, [ 6 , 88 ] beyond requirements of most electrochemical energy storage devices.
Another promising system is about sulfide solid state electrolytes with the high conductivity and negligible grain boundary, even when prepared by cold pressing. The main limitation of the system is its stability to electrodes, including the (electro)chemical reaction and space charge layer problems. One effective solution is to apply different solid state electrolytes to satisfy various demands of cathodes and anodes, [ 100 , 132 , 345 ] and another is to introduce the buffer layer into the interface between the electrode and electrolyte. [ 349 – 351 ]
Considering the environmental safety of the fabricating process and practical applications, oxides often attract the more extensive attention. However, oxides usually have high grain boundary resistance, and the higher density with less grain boundary can only be obtained by sintering at high temperature for a long time, resulting in higher cost. Replacing the ceramic by glass or glass-ceramic is an effective and economical way to eliminate the grain boundaries. [ 75 – 78 ] In addition, oxides usually have higher mechanical strength, leading to the point contact with electrodes and high interface resistance. One solution is to mix the oxides and sulfides together and take advantage of both of them: low resistance of bulk and grain boundary, together with high chemical stability, and can be fabricated by cold pressing with the lower cost. In addition, the good ductility of the mixture contributes to the better physical contact with electrodes. [ 335 ] As for the NASICON and perovskite families, the compositions with highest conductivity usually contain Ti 4+ , which is not stable to anodes with low potential. [ 343 , 344 ] LLZO in the garnet family has relatively high conductivity, free from Ti, resulting in good chemical stability. However, when LLZO is applied in an all-solid-state battery, the interface resistance is usually very high due to the bad physical contact and space charge layer effect. Also, another reason was proposed by a recent study, which indicates that low conductivity can arise from the formation of Li 2 CO 3 in the condition of humidity. [ 356 ] If this is so, smaller bulk and more boundaries can increase the conductivity, and fine control of structure can be realized during the preparation process. [ 357 ]
For inorganic materials, the interface contact resistance is always a difficult problem. In addition, despite the higher hardness of inorganic materials, they are short of flexibility, which causes many challenges in the practical applications of full cells: How to match the volume change with electrodes during the Li ions’ intercalating/deintercalating? How to match the thermal expansion arising from the increase of temperature under work? For (hybrid) electrical vehicles and other mobile devices, how to solve the ceramic fragmentation and short circuit problems ascribed to sudden shock? Considering all the problems above, organic polymers have unrivalled superiority in the aspects of flexibility and elasticity. Combining the advantages of polymers and ceramics may be the silver bullet. [ 266 , 358 – 361 ] Common polymers used today have a narrow electrochemical window and low conductivity, and the large volume fraction restricts the energy density. In contrast, liquid electrolytes (including organic electrolytic solution and ionic liquid) promise to reach higher conductivity. In addition, they may have better wettability of electrodes, and can improve the contact performance greatly by adding a relatively small amount in response to the safety problem (for organic electrolytic solution). Therefore, the composition of liquid and solid may be a further direction for research. [ 362 ]
6.2. Synthesis and characterization
For a certain material system, optimizing the composition and doping ratio is usually an important to improve conductivity. However, exploring the optimizal point in the composition phase diagram is very difficult and requires much work for a long time. The combinatorial materials science infrastructure is set up to raise the efficiency. Dahn research group in Canada used the 64-channel combinatorial electrochemical cell for high-throughput screening of materials for use as Li-ion rechargeable battery electrodes. [ 363 ] The technique was also applied to study the solid-solution LiFe 1− x Mn x PO 4 cathodes. [ 364 ] Now, Xiaodong Xiang and Peter Schultz of Lawrence Berkeley National Lab have developed and improved the Combinatorial Material Processing to realize the simultaneous growth and characterization of thousands of compositions of novel material. [ 365 – 368 ] Another high-throughput synthesis and characterization method, called the Diffusion-Multiple Approach, was developed by Jicheng Zhao of General Electric Company (GE). [ 369 – 372 ]
Experimental methods to investigate the diffusion mechanism can be grouped into direct measurement and indirect measurement. The former is mainly based on tracer atom detection, although all the methods employed so far, such as serial sectioning or SIMS depth profiling, are destructive and ex situ . Indirect methods usually give the average results of microscopic mechanism, without spatial resolution for polycrystals. The methods adopting microelectrodes or nanoelectrodes can map the full space and find the statistical relationship between conductivity and structure in various microstructures. [ 284 ] Annular bright field imaging using aberration-corrected scanning transmission electron microscopy (ABF-STEM) is the best method so far to detect Li, providing the opportunity to picture the atomic space motion. However, for the application in solid state electrolytes, difficulty occurs for the low electronic conductivity of samples, leading to e-beam damage. [ 342 ] Note that it is still questionable whether the damage can be controlled. Further, 4D ultrafast electron microscopy introduces the time dimension, [ 373 ] which becomes a new hot spot of the development of electron microscopy after ABF-STEM. This method combines the TEM in atomic resolution with ultrafast laser technologies as well as in situ technique and can realize the spatial resolution in pm and time resolution in ps. Scanning tunnel microscopy (STM) can be applied to in situ observation of Li-ion motion at the surface, as well as motion induced by electric field. If experiments can be designed for in situ dynamic study, it will be of great help to understand the transport mechanism. However, the problem still lies in the low electronic conductivity of sample.
6.3. Theory and calculation
From the development history of solid electrolytes, it seems that the understanding of ion diffusion mechanism may be driven by the emergence of novel materials. Ions rather than electrons become the mobile carriers, leading to the set up of defect chemistry. In order to explain the abnormal high conductivity, sublattice melting picture was introduced. In order to interpret the anomalies in experiments, such as the broadening of quasielastic spectral line, and the odd relationship between the conductivity and frequency in the high frequency region, multiple dynamic models were proposed with the consideration of many-body interaction. The ion diffusion mechanism models were continually revised with the improvement of characterization methods, although the current theoretical model cannot give the analytic solution. Therefore, it is a great challenge to build effective simplified models to balance the accuracy and time cost. In fact, the mechanisms of various systems are quite different. So the key to building rational models is to extract more effective information from experiments and characterization.
There are still important problems that cannot be solved by current experimental methods, considering the technological limits and the time and monetary cost. In contrast, along with the rapid development of computer technology and information science, theory–model–calculation-simulation has become a powerful supplement of experiments. The Materials Genome Initiative (MGI) aims at integrating the experiment, calculation and database together, among which calculation is important. [ 374 , 375 ] As defined by Alpaydin in 2004, machine learning is “programming computers to optimize a performance criterion using example data or past experience”. With the process of machine learning, the ultimate goal of MGI is to realize the rational design of materials, including the discovery of novel materials as well as the performance optimization (e.g., interface design or size design, and so on) of existing ones. Note that when the size is reduced to nanometers, the material properties usually change abnormally due to size effects. Quantification of the size effect is influenced by the specific size and shape of materials, which adds two dimensions to the structure–performance relationship. Recently, Qian et al. proposed the concept of Nanomaterials Genome Initiative (NMGI) with the consideration of the size and shape dimension, as shown in Fig. Circos diagram of Nanomaterials Genome (a) composition-structure and (b) size-shape relations. [ 376 ]
Reference
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 | |
| 67 | |
| 68 | |
| 69 | |
| 70 | |
| 71 | |
| 72 | |
| 73 | |
| 74 | |
| 75 | |
| 76 | |
| 77 | |
| 78 | |
| 79 | |
| 80 | |
| 81 | |
| 82 | |
| 83 | |
| 84 | |
| 85 | |
| 86 | |
| 87 | |
| 88 | |
| 89 | |
| 90 | |
| 91 | |
| 92 | |
| 93 | |
| 94 | |
| 95 | |
| 96 | |
| 97 | |
| 98 | |
| 99 | |
| 100 | |
| 101 | |
| 102 | |
| 103 | |
| 104 | |
| 105 | |
| 106 | |
| 107 | |
| 108 | |
| 109 | |
| 110 | |
| 111 | |
| 112 | |
| 113 | |
| 114 | |
| 115 | |
| 116 | |
| 117 | |
| 118 | |
| 119 | |
| 120 | |
| 121 | |
| 122 | |
| 123 | |
| 124 | |
| 125 | |
| 126 | |
| 127 | |
| 128 | |
| 129 | |
| 130 | |
| 131 | |
| 132 | |
| 133 | |
| 134 | |
| 135 | |
| 136 | |
| 137 | |
| 138 | |
| 139 | |
| 140 | |
| 141 | |
| 142 | |
| 143 | |
| 144 | |
| 145 | |
| 146 | |
| 147 | |
| 148 | |
| 149 | |
| 150 | |
| 151 | |
| 152 | |
| 153 | |
| 154 | |
| 155 | |
| 156 | |
| 157 | |
| 158 | |
| 159 | |
| 160 | |
| 161 | |
| 162 | |
| 163 | |
| 164 | |
| 165 | |
| 166 | |
| 167 | |
| 168 | |
| 169 | |
| 170 | |
| 171 | |
| 172 | |
| 173 | |
| 174 | |
| 175 | |
| 176 | |
| 177 | |
| 178 | |
| 179 | |
| 180 | |
| 181 | |
| 182 | |
| 183 | |
| 184 | |
| 185 | |
| 186 | |
| 187 | |
| 188 | |
| 189 | |
| 190 | |
| 191 | |
| 192 | |
| 193 | |
| 194 | |
| 195 | |
| 196 | |
| 197 | |
| 198 | |
| 199 | |
| 200 | |
| 201 | |
| 202 | |
| 203 | |
| 204 | |
| 205 | |
| 206 | |
| 207 | |
| 208 | |
| 209 | |
| 210 | |
| 211 | |
| 212 | |
| 213 | |
| 214 | |
| 215 | |
| 216 | |
| 217 | |
| 218 | |
| 219 | |
| 220 | |
| 221 | |
| 222 | |
| 223 | |
| 224 | |
| 225 | |
| 226 | |
| 227 | |
| 228 | |
| 229 | |
| 230 | |
| 231 | |
| 232 | |
| 233 | |
| 234 | |
| 235 | |
| 236 | |
| 237 | |
| 238 | |
| 239 | |
| 240 | |
| 241 | |
| 242 | |
| 243 | |
| 244 | |
| 245 | |
| 246 | |
| 247 | |
| 248 | |
| 249 | |
| 250 | |
| 251 | |
| 252 | |
| 253 | |
| 254 | |
| 255 | |
| 256 | |
| 257 | |
| 258 | |
| 259 | |
| 260 | |
| 261 | |
| 262 | |
| 263 | |
| 264 | |
| 265 | |
| 266 | |
| 267 | |
| 268 | |
| 269 | |
| 270 | |
| 271 | |
| 272 | |
| 273 | |
| 274 | |
| 275 | |
| 276 | |
| 277 | |
| 278 | |
| 279 | |
| 280 | |
| 281 | |
| 282 | |
| 283 | |
| 284 | |
| 285 | |
| 286 | |
| 287 | |
| 288 | |
| 289 | |
| 290 | |
| 291 | |
| 292 | |
| 293 | |
| 294 | |
| 295 | |
| 296 | |
| 297 | |
| 298 | |
| 299 | |
| 300 | |
| 301 | |
| 302 | |
| 303 | |
| 304 | |
| 305 | |
| 306 | |
| 307 | |
| 308 | |
| 309 | |
| 310 | |
| 311 | |
| 312 | |
| 313 | |
| 314 | |
| 315 | |
| 316 | |
| 317 | |
| 318 | |
| 319 | |
| 320 | |
| 321 | |
| 322 | |
| 323 | |
| 324 | |
| 325 | |
| 326 | |
| 327 | |
| 328 | |
| 329 | |
| 330 | |
| 331 | |
| 332 | |
| 333 | |
| 334 | |
| 335 | |
| 336 | |
| 337 | |
| 338 | |
| 339 | |
| 340 | |
| 341 | |
| 342 | |
| 343 | |
| 344 | |
| 345 | |
| 346 | |
| 347 | |
| 348 | |
| 349 | |
| 350 | |
| 351 | |
| 352 | |
| 353 | |
| 354 | |
| 355 | |
| 356 | |
| 357 | |
| 358 | |
| 359 | |
| 360 | |
| 361 | |
| 362 | |
| 363 | |
| 364 | |
| 365 | |
| 366 | |
| 367 | |
| 368 | |
| 369 | |
| 370 | |
| 371 | |
| 372 | |
| 373 | |
| 374 | |
| 375 | |
| 376 |