† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 51225204 and 21303222), the Shandong Taishan Scholarship, China, the Ministry of Science and Technology, China (Grant No. 2012CB932900), and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA09010000).
Size-related properties of novel lithium battery materials, arising from kinetics, thermodynamics, and newly discovered lithium storage mechanisms, are reviewed. Complementary experimental and computational investigations of the use of the size effects to modify electrodes and electrolytes for lithium ion batteries are enumerated and discussed together. Size differences in the materials in lithium ion batteries lead to a variety of exciting phenomena. Smaller-particle materials with highly connective interfaces and reduced diffusion paths exhibit higher rate performance than the corresponding bulk materials. The thermodynamics is also changed by the higher surface energy of smaller particles, affecting, for example, secondary surface reactions, lattice parameter, voltage, and the phase transformation mechanism. Newly discovered lithium storage mechanisms that result in superior storage capacity are also briefly highlighted.
Exciting differences appear in reduced-size materials. The observable differences include a significantly great ratio of surface/interface to volume, excellent enhancement of surface energy, variation of lattice constant, greater defect concentration, and so on. The observable changes mentioned above may cause some magical effects such as the quantum size effect, the coulomb blockade, the quantum tunneling effect, and the dielectric confinement effect. Indeed, these unique size efforts have been studied in multiple fields, including chemistry, physics, biology, electronics, and battery material design. The design of Li ion batteries with excellent performance requires orchestrating knowledge from multiple disciplines. The size effects in Li ion battery materials also alter various battery properties such as the power density.
With the ceaseless development of portable electronics and the deployment of electric vehicles, considerable attention is paid to electrochemical energy storage with high power density. Micrometer-sized electrode materials cannot satisfy the requirements to charge/discharge rapidly due to the poor kinetics. It is well known that the size effects in materials can overcome this restriction by shortening the diffusion lengths of both electrons and Li ions, increasing the area of contact between the electrode and electrolyte, enhancing structural stability, and so on. [ 1 ] The inactive materials may even turn to active ones by reducing their sizes. But there are accompanying disadvantages such as low thermodynamic stability and intense side reactions. The superior performance of variously sized Li ion battery materials has attracted widespread attention.
The present review highlights the enhanced performance arising from the reduced particle size, the associated mechanisms, and new lithium storage mechanisms. To provide compelling detail, we will discuss a range of experimental and computational evidences.
Varying materials’ size changes the kinetics and thermodynamics of both electrodes and electrolytes.
In the kinetic process of Li ion batteries, ion diffusion in the electrode, called the rate-determining step, determines the speed of the primary electrochemical reaction. The relation among the mean diffusion time of Li ions ( τ ), the diffusion coefficient ( D ), and the diffusion length ( L ) is given as
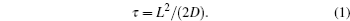
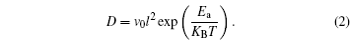
Shortening the diffusion length is commonly used to improve the rate performance of the conventional Li ion battery materials. [ 2 – 4 ] For example, the conventional cathode material LiFePO 4 has been studied extensively because of its high theoretical energy density of 580 W·h/kg. However, it suffers from low electronic and ionic conductivities. Wu et al. reported that a nanocomposite with highly dispersed nanoparticles of LiFePO 4 in a nanoporous carbon matrix can be fully charged or discharged within a period of less than 30 s. [ 2 ] The extremely high power is enabled by nanometer-sized LiFePO 4 particles, which shorten the Li ion diffusion path, and by quick Li + /e – diffusion, which arises from the nature of the nanoporous carbon matrix. [ 2 ]
Size reduction not only improves the rate performance of some electrode materials, but also endows some inactive materials such as rutile TiO 2 with electroactivity. [ 5 , 6 ] Rutile is the most stable structure of TiO 2 under standard conditions, but Li insertion into rutile is usually reported to be negligible. The capacity can be significantly improved by nanocrystallization. [ 5 , 7 , 8 ] Hu et al. reported observing high capacity, excellent capacity retention during cycling, and high rate performance for rutile TiO 2 needles about 10 nm in diameter and 30 nm in length. [ 5 ]
Besides the reduced diffusion length, another reason for the higher intercalation/deintercalation rates of some nanomaterials is the increased contact area, which promotes Li ion exchange. The excellent performance of nanoscale Li 4 Ti 5 O 12 is a suitable example. Li 4 Ti 5 O 12 is an attractive anode material due to its low cost, zero strain, and operating voltage plateau which are sufficient to avoid the formation of lithium dendrites and solid electrolyte interface (SEI). However, it suffers from a moderate Li ion diffusion coefficient and poor electronic conductivity, which is also indicated by the band gap of about 2 eV calculated by ab initio study. [ 9 ] The nanocrystalline Li 4 Ti 5 O 12 prepared by combustion synthesis exhibits high rate capability and good capacity retention, both of which can be attributed to the presence of highly porous nanostructures having BET surface areas of about 12 m 2 /g. [ 10 ]
The electron exchange can also be improved by enhancing the contact area between the active materials and the conductive additives. Zhang et al. improved the effective contact area by connecting one-dimensional carbon nanofibers with zero-dimensional carbon black to build a conductive network, which is established within the Li 4 Ti 5 O 12 particles by the penetrating multiple carbon nanofibers, and the carbon black particles attached onto the surface of the Li 4 Ti 5 O 12 particles fill in the gaps between them. [ 11 ]
The materials with one-dimensional Li diffusion channel may exhibit high rate performance if the orientation of matter is controlled to improve the exposed area with high pore density for Li insertion/extraction. [ 12 ]
The diffusion coefficient is also affected by nanocrystallization in some cases. Based on their computational results for LiFePO 4 , Malik et al. suggested that the kinetic benefit of small scale materials results from both shortened transport paths and enhanced diffusion constants of one-dimensional channel materials. The phenomenon will be introduced very briefly in the section below on theoretical calculation. [ 13 ]
The dynamic performance of any nanoscale electrodes should be dramatically improved in theory, but it is not actually the case for some electrode materials due to the thermodynamic instability that comes with size reduction.
Due to an abundance of dangling bonds, a large surface free energy, a high density of defects, and the high surface-to-volume ratio of nanostructured electrode materials, the risk of secondary reactions is dramatically high, leading to a short life cycle and consuming much of the Li supplied by the cathodes.
Nano LiCoO 2 exhibits worse cyclability than bulk LiCoO 2 due to the presence of SEI film, formed mainly in spontaneous chemical reactions between the solvent molecules and nanoscale LiCoO 2 . [ 14 , 15 ] Furthermore, it has been found in many nanostructured transition metal oxides that thick SEI films formed during Li uptake may disappear completely upon Li extraction, which leads to capacity fading and safety problems. Therefore, surface modifications must be considered for nanostructured transition metal oxides. For instance, carbon coated Fe 3 O 4 nanospindles exhibit very high specific capacity, superior cycling performance, and high rate performance because the carbon coating enhances electronic conductivity and stabilizes the SEI films. [ 16 ]
The abundant agglomerates that lead to the irreversible fading of capacity and shortened cycle life will occur, and they occur during the preparation processes or electrochemical cycling.
Surface coating and the formation of nano/micro hierarchical structures are efficient techniques to avoid agglomeration, on account of the formation of highly dispersed nanocrystals in the matrix. [ 16 , 17 ] For example, Guo et al. proposed that a conducting 3D network (a sketch is shown in Fig.
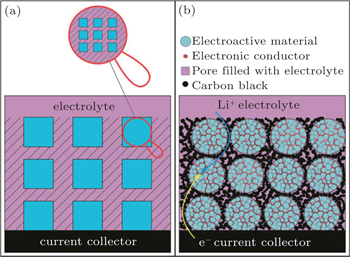 | Fig. 1. (a) Schematic of the desired design; the shaded areas represent 3D conductive networks. (b) Sketch of a realistic composite in which Li + /e – can transfer to most of the electroactive material particles through the 3D conductive networks. [ 17 ] |
Lattice expansion dependent upon particle size is observed in some materials; however, explanations vary, including a change of bond length, a reduction of atomic charge, and so on. [ 15 , 18 , 19 ] According to magnetic susceptibility measurements, the fact that 20% of the cobalt at the surface layer is Co 2+ ions can explain the lattice expansion of nanocrystalline LiCoO 2 , because the Co 2+ –O distance is longer than the Co 3+ –O distance. [ 15 ] Variation of the lattice parameter also impacts Li ion diffusion kinetics, since it changes the channel size.
The thermodynamic equilibrium voltage ( V ) is related to the difference of chemical potential (Δ μ ) between the reactants and products
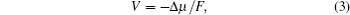
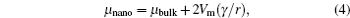
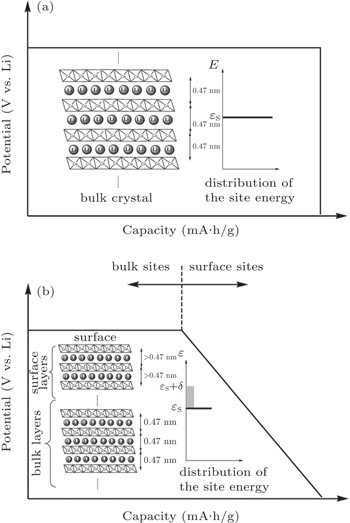 | Fig. 2. (a) Structure sketch and expected discharge curve for bulk LiCoO 2 , in which the site energy is considered to be a constant ε S . (b) Structure sketch and expected discharge curve for nanoscale LiCoO 2 . The fluctuation of the site energy is represented by δ . [ 15 ] |
Defect energy not only impacts the thermodynamic equilibrium voltage of a given structure, but also results in the reversal of the stable morphology of a material, like Fe 2 O 3 . The phase transition from maghemite ( γ -Fe 2 O 3 ) to hematite ( α -Fe 2 O 3 ) has been observed in situ in XRD as the crystal size varies from 9 nm to 16 nm due to the Gibbs-energy change. [ 23 ]
Phase transition behavior is also connected with the size of material particles. Varied staging phenomena have been observed in different-sized particles of LiFePO 4 , which is widely considered to be a typical first-order phase transition material. [ 24 ] The staging structure is an intermediate phase between LiFePO 4 and FePO 4 for large crystals or a uniform phase throughout the whole particle for small particles. The distinctive configuration, a thermodynamically metastable but kinetically controlled state, was also explained by density functional theory calculations. [ 25 ] The formation of the lithium staging configuration is mainly attributed to the interaction between the effective oxidation state of Fe redox and the arrangement of Li ions. [ 25 ] By calculating the magnitude of the overpotential, Ceder et al. determined that only minimal overpotential is required to enable the single-phase transformation path of LiFePO 4 at room temperature and they explained the difference between larger particles stabilizing intraparticle two-phase coexistence and smaller particles favoring interparticle two-phase coexistence. [ 26 ] Kobayashi et al. indicated that the particle size determines which primary factor will dominate the electrochemical behavior of LiFePO 4 . [ 27 ] Bulk miscibility dominates the electrochemical behavior of Li x FePO 4 with particle sizes larger than 40 nm, but the geometric surface portion becomes evident when the particles are smaller than 100 nm.
Despite the existence of thermodynamic instability, nanometer scale can play yet another favorable role in some aspects of thermodynamic behavior, such as improving the mechanical strength as an excellent strain accommodation during charge/discharge. A plenty of internal cavities or pores can tolerate the volume expansion/contraction associated with lithiation/delithiation. Silicon is an important candidate anode material for the next generation of Li ion batteries because of its extremely high theoretical capacity (4200 mA·h/g), realized by the formation of Li 4.4 Si. However, the reversible capacity of silicon anodes is very poor due to huge volume expansion (> 300%) during the lithiation of silicon, which pulverizes the electrode material, leading to fading capacity. The pulverization of Si resulting from volume changes can be mitigated by integrating particles smaller than 150 nm, as the expansion/contraction of single nanoparticles is much smaller than that of larger particles. [ 28 – 31 ] Li et al. reported that a composite of nanoscale silicon power and carbon black exhibits an extremely high reversible capacity of 1700 mA·h/g and excellent cyclic performance. [ 28 ] The smaller the particles, the larger the surface-to-volume ratio, accommodating a greater charge and more lithium ions. This fact significantly reduces the lithium ion diffusion distance during charging/discharging, which can greatly reduce the volumetric changes and increase the structural stability, because the structure at the surface is generally more favorable for the diffusion of lithium ions because the diffusion energy of lithium migration is generally higher in the bulk region than near the surface. [ 32 ]
The increased reversible capacity of nanomaterials originates both from good structural stability and from new lithium storage mechanisms.
One of the new mechanisms is the conversion mechanism, which can be used to explain the excellent lithium storage capacity of nanoscale transition metal oxides, fluorides, sulfides, nitrides, and other polyanion compounds. [ 33 ] For amorphous R VO 4 ( R = In, Cr, Fe, Al, Y), a model based on the formation of Li–O bonds has been proposed to account for the large Li acceptance that was found in a survey of experimental results. [ 34 ] On this basis, Poizot et al. reported that the excellent capacity (700 mA·h/g) of nanoscale transition metal oxides M O ( M = Co, Ni, Cu, Fe) electrodes stems from the formation/decomposition of Li 2 O that occurs with the reduction/oxidation of metal nanoparticles. For transition metals, thermodynamic calculations based on the conversion mechanism for different binary transition metal oxides and fluorides predicted an increase of cell voltage with increasing atomic number. [ 35 ]
With the generation of lithiated-state Li 2 O or transition metal, the lithium storage capacity is commonly thought to be fully occupied, because it is assumed that the storage material cannot accommodate any more lithium. However, the capacity can be raised further by another lithium storage mechanism (interfacial lithium storage).
Interfacial lithium storage mechanism that Li ions and electrons store on the each side of the interface during lithiation process plays a large role in the overall capacity of nanostructural materials due to the comparatively large total interface area of the nanoparticles. Ab initio atomic and electronic structure calculations of Ti(0001)/Li 2 O(111) indicated that the interface can store lithium, and a huge transfer of electrons to the Ti adatoms was clearly revealed by 2D difference electron density maps. [ 36 ] The interfacial lithium storage mechanism proposed by Jamanik and Maier was confirmed experimentally by the 6 Li magic angle spinning nuclear magnetic resonance of the lithiation process of nanocrystalline RuO 2 . [ 37 ]
The third lithium storage mechanism resulting from size reduction is based on the space for lithium ions in the abundant three-dimensional defects such as nanopores or cavities. The size effects might be thought to enhance the properties of electrodes only, yet they also benefit the electrolytes of Li ion batteries.
As mentioned above, the practical uses of small materials suffer from intense side reactions and low thermodynamic stability. Solid electrolyte batteries pose a solution, in that the interface between an electrode and a solid electrolyte is more stable. But, solid electrolytes have not been widely used because of their low ionic conductivity and high interfacial resistance. Partial atomic substitution is an effective technique to improve the ionic conductivity, e.g. the substitution of Ge atoms for P atoms in lithium thiophosphate forms Li 10 GeP 2 S 12 , which has unsurpassed ionic conductivity of 1.2 × 10 –2 S/cm, however its chemical compatibility with lithium metal is decreased because of the presence of Ge in the structure. Compared with atomic substitution, reduced size is a more feasible strategy for getting high ionic conductivity in solid electrolytes without disrupting chemical stability. For example, Liu et al. enhanced room-temperature lithium ion conductivity by three orders of magnitude by creating nanoporous Li 3 PS 4 , which exists stably in its preferred metastable phase and provides a significant surface conduction mechanism. [ 38 ]
Electrolyte composites of liquid non-aqueous salt solutions and solid insulating particles exhibit enhanced conductivity. The phenomenon is attributed to anisotropic forces at the interface between the liquid electrolyte and solid particles, forces which result in space charge areas and dipole effects at high ratio. [ 39 ] In the mechanism discussed above, the effect of insulating particles of smaller size is more prominent due to the higher surface-to-volume ratio.
The size effects appearing in Li ion batteries are thought to be caused mainly by the high surface-to-volume ratio, but distortions of atomic or electronic structure at the surface also result in performance changes at a microscopic level. These microscopic changes, difficult to observe in experiment, can be studied by theoretical calculation.
Computational methods play a vital role in predicting the structures and properties of materials and suggesting approaches to their modification, all of which are critical for breakthroughs needed for the next generation of Li ion batteries.
It is well known that the morphology of some materials, like the various forms of TiO 2 mentioned above, can have an excellent effect on special properties. To explore the significant enhancement of the surface ratio as the size is reduced, the structural differences between the surface state and bulk state are studied by theoretical calculation. [ 40 – 43 ] The differences are prominent on account of the changes in coordination among the atoms at the surface. The exposed surface orientation and terminations need to be determined at first according to the surface energy difference. Since the difference between the Gibbs energy and the total energy is negligible for solid phases, the surface energy can be calculated by
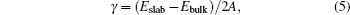
It is difficult to calculate the surface energy of nonstoichiometric slabs since the chemical potentials need to be considered to determine E bulk . A detailed introduction can be found in Ceder’s work. [ 44 ]
The equilibrium shape of nanoparticles can be determined according to the surface energies mentioned above by means of Wulff’s construction. Seriani et al. reported that Li 2 O and Li 2 O 2 nanoparticles take the forms of octahedra and hexagonal prisms, respectively. [ 45 ] Computational techniques can also simulate the process of nucleation, modeling nanoclusters of different sizes, like the reported nanoparticulate oxides and sulfides. [ 46 ]
The electronic structure of nanoparticles may differ significantly from that of the bulk phase. Changes in the electronic spin state and oxidation state of a cation may appear as the particle size is reduced, due to a decreased ion coordination number at the surface, stemming from surface bonds breaking and reforming. Qian et al. reported that electronic spin state transitions occur at the surfaces of stoichiometric LiCoO 2 , where an intermediate spin state on the square pyramid coordinated site turns into a high spin state on a pseudotetrahedrally coordinated site for trivalent cobalt ions adjacent to the surface. [ 47 ] When Co 3+ near the surface is in either the intermediate or high spin state explained by the modification of the crystal field splitting of Co(d) orbitals at the surface due to the missed Co–O bonds, the surface energy is decreased and the energy gap between the occupied and unoccupied states of Co ions is also minimized. [ 47 ]
The change of electronic state between bulk material and surface structure do not have to be accompanied by the breakage of bonds. Ouyang et al. reported that one fourth of Mn ions at the λ -MnO 2 (001) surface undergo a change of oxidation state from +4 to +3 with the surface reconstruction, which does not change the Mn coordination number with oxygen. [ 48 ]
Although a voltage change with nanocrystalline can be observed in experiments today, a change in atomic level can be predicted only by theoretical calculations. For nanocrystalline Li 4 Ti 5 O 12 , Ganapathy et al. calculated the Li ion insertion voltage profile of the defective spinel Li 4 Ti 5 O 12 and explained the high Li insertion voltage of surface Li storage. Lithium insertion into the subsurface layers of Li 4 Ti 5 O 12 (100) (110) and (111) surfaces is allowed at voltages larger than the average insertion voltage. The higher capacities of nanoscale Li 4 Ti 5 O 12 can be explained by the fact that (111) surface capacity can exceed bulk capacity. Based on these calculation results, it is predicted that increasing the relative number of (111) facets by reducing the size and tailoring the shape will significantly increase the storage capacity. [ 49 ]
The improved kinetic performance resulting from nanocrystallization is always explained by shortened diffusion length, but the diffusion coefficient is usually considered to be constant. However, the diffusion coefficient is also affected by a decrease in size in some cases. In one-dimensional diffusion material, diffusion is impeded by the presence of immobile and low-mobility defects in the diffusion path which do not appeared in 2D or 3D diffusion material since the active ion can simply move around the defect. The calculated association between the unblocked capacity fraction and channel length, shown in Fig.
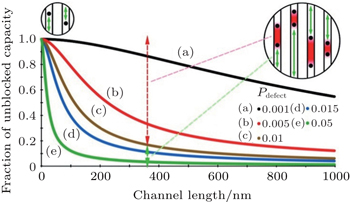 | Fig. 3. Predicted association between unblocked capacity and channel length in LiFePO 4 for various defect concentrations. [ 13 ] |
Most active ions can diffuse through channels in small particles because most of the channels contain one or zero defects. However, most Li ion sites are not directly accessible from the surface in large materials. If most channels are blocked, the macroscopic diffusion constant is zero according to D ∼ L 2 /2 τ because τ is a long time. It is suggested that the kinetic benefit of small-particle materials originates from the shortened transport paths and the enhanced diffusion constants of one-dimensional-channel materials whenever point defects are present. [ 13 ]
The size effects exhibited in battery material can be directly observed in experiment. But the mechanisms behind them are difficult to determine in experiment. So theoretical calculations are used to explain the effects of size on performance, e.g., theoretical calculations about the difference in Li intercalation between bulk β -MnO 2 and nanoscale β -MnO 2 . It is difficult to understand why bulk β -MnO 2 can intercalate only a little lithium or none at all, since the migration barrier of Li ions in bulk β -MnO 2 is only 0.17 eV, which one would expect to contribute to good performance as a lithium intercalation cathode. Tompsett et al. found that the migration of Li ions in bulk β -MnO 2 is primarily one-dimensional along the c -axis tunnels and the route of easy c -axis migration is available only at the (101) surface and symmetrical equivalents. [ 50 ] The initial barrier to Li ion insertion at the surface is about 0.6 eV, which is the key factor in the intercalation behavior of nanostructured versus bulk β -MnO 2 . [ 50 ] The superior cyclic stability found in mesoporous or nanoscale β -MnO 2 likely stems from greater exposure of these surfaces. [ 50 ]
It is also difficult to understand the varied experimental findings about the phase orientation of LiFePO 4 single particles. [ 51 – 53 ] Abdellahi et al. pointed out that the varied results originate in that both the chemical interfacial energy and the coherency strain energy scale in different ways with varying particle size (the former being proportional to the interfacial area and the latter to the particle volume), and each may favor different interface orientations. [ 54 ] So the phase orientation of LiFePO 4 single particles depends upon both particle size and particle morphology.
Although not the focus of this review, it is also worth noting that the size effects described here are exhibited more observably in other energy storage devices [ 55 , 56 ] and other metal ion batteries, such as Na +[ 57 – 59 ] and Mg 2+ . [ 60 , 61 ] It must also be pointed out that some size effects in batteries are not addressed in detail because of the great variation in size effects, such as the degree of difficulty for doping, the special Li insertion sites, and so on.
The differences in materials as size changes have a variety of aspects, such as diffusion length, surface to volume ratio, atomic configuration, and electronic structure. Size effects appear in both the electrodes and electrolytes of Li ion batteries. The performance changes associated with decreasing size may be either advantages (such as enhanced kinetic activity) or disadvantages (such as low thermodynamic stability and intense side reactions). Because of the intense side reactions and low thermodynamic stability, the practical use of small size materials requires both a comprehensive understanding of the size effects and breakthroughs in concepts and technology, such as the realization of all-solid electrolyte batteries with their more stable electrode–electrolyte interface. For contemporary studies of the mechanism behind the size effects, the combination of experimental means and computational techniques has become vital, as the microscopic distinctions are difficult to observe through conventional experimental measurements. Understanding various size effects and mechanisms requires more research from a range of disciplines, and it would lead to genuine development of nanoscale or other size materials and then promote progress toward a new generation of Li ion batteries with a leap in either energy density or power density.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 |


