† Corresponding author. E-mail:
Project supported by the Beijing S&T Project, China (Grant No. Z13111000340000), the National Natural Science Foundation of China (Grant Nos. 51325206 and 11234013) and the National Basic Research Program of China (Grant No. 2012CB932900).
Physical models of ion diffusion at different interfaces are reviewed. The use of impedance spectroscopy (IS), nuclear magnetic resonance (NMR), and secondary ion mass spectrometry (SIMS) techniques are also discussed. The diffusion of ions is fundamental to the operation of lithium-ion batteries, taking place not only within the grains but also across different interfaces. Interfacial ion transport usually contributes to the majority of the resistance in lithium-ion batteries. A greater understanding of the interfacial diffusion of ions is crucial to improving battery performance.
Due to energy shortages and environmental pollution, highly efficient, clean energy technologies have attracted considerable attention in recent years. Lithium-ion batteries stand out among these technologies, with high energy density and high conversion efficiency. Their improvement is currently widely pursued for vehicles and grid applications. Also, consumers demand thinner, lighter, space-effective, and flexible batteries. The improvement of lithium-ion batteries requires deeper understanding of the basic physical processes, which include electrochemical reaction, ion diffusion, structure evolution, and volume change. [ 1 ]
Lithium-ion diffusion is a principal physical process in lithium-ion batteries. The ion diffusion takes place not only in the crystalline lattice of electrodes and liquid electrolytes, but also at interfaces, such as grain boundaries and electrolyte/electrode interfaces. Resistance from interfacial diffusion is the majority of the inner resistance of lithium-ion batteries, because in most cases, interfacial diffusion is slower than the dynamic process in a homogenous structure. [ 2 , 3 ] A full understanding of the physical mechanism of ion diffusion at interfaces is very important to developing the next generation of high-performance batteries.
The interfaces in a battery system include grain boundaries in polycrystalline electrode, grain boundaries in polycrystalline solid electrolyte, interfaces between liquid electrolyte and solid electrode, and interfaces in different composite electrolytes (composite electrolytes include a polymer and different inorganic solid electrolytes). Since different interfaces have different components and structures, the physical mechanism of ion diffusion is different. In this paper, the transport mechanisms at different interfaces are discussed, and the corresponding physical models for interfacial diffusion are reviewed. In order to fully understand the transport mechanism, experimental techniques to distinguish interfacial diffusion from bulk diffusion are necessary. Different physical techniques are also presented.
An inorganic crystalline material is structured by a symmetric, periodic lattice. Because of thermal vibrations, lithium ions may shift off the equilibrium center and hop into an adjacent vacant lattice site or interstitial site. If an electrical gradient field exists across the crystalline lattice, a net diffusion along the electrical direction will result from random hopping, which leads to long-range ionic transport. [ 4 ] The hopping of ions usually happens along adjacent lattice sites where the lowest energy barrier exists. Because of the symmetric, periodic arrangement of a crystalline structure, the diffusion pathway can be extrapolated from the analysis of ion hopping in a unit cell.
In polycrystalline materials, the symmetric and periodic structures end at the edge of a single crystal. The area connecting two crystals is called a grain boundary, and its elemental composition and structure may be dramatically different from the grain. In terms of symmetry and thickness, grain boundaries can be divided into several types. (i) Grain boundary which has a highly defective and distorted crystal structure, in which the atom coordination decreases but the long periodical structure can still be found. The thickness of such a grain boundary is less than that of a unit cell, or even nearly a single-atom layer. (ii) Grain boundary consisting of atoms that are randomly arranged, without any periodicity. This type of grain boundary is only several atoms thick. (iii) Grain boundary with crystalline periodic atomic arrangement. The thickness is larger than a single unit cell. (iv) Amorphous grain boundary with disordered atomic arrangement. This type of grain boundary is also more than several atoms thick. [ 5 – 8 ]
The concentration of charge carriers, charge mobility, diffusion pathway, and activation energy are all different at interfaces. In order to further understand the different diffusion properties at grain boundaries, several physical models are introduced. According to the structural properties of polycrystalline substances, Beekmans and Heyne proposed the Brick layer model (as shown in Fig.
 | Fig. 1. (a) Brick layer model for polycrystalline ceramic; (b) possible ion diffusion pathways: (i) across grain and grain boundary, (ii) along grain boundary. [ 12 ] |
 | Fig. 2. (a) Defect concentration profile near the interface based on space charge layer model; (b) model microstructure for a polycrystalline solid. [ 12 ] |
In 1973, Liang found that the ionic conductivity of LiI increased upon being prepared as a composite with Al 2 O 3 , as shown in Fig.
 | Fig. 3. The conductivity of LiI–Al 2 O 3 as a function of Al 2 O 3 content. [ 13 ] |
 | Fig. 4. Percolation model of an ionic conductor at different concentrations dispersed in insulating material. Insulator is shown in gray and ionic conductor is shown in white. [ 14 , 15 ] |
 | Fig. 5. The resistance network model. [ 16 ] |
 | Fig. 6. Morphology model for composite electrolyte. [ 17 ] |
Batteries with hybrid electrolytes are considered to be the next generation for large-scale energy storage. [ 18 , 19 ] In a hybrid electrolyte battery, a solid-state electrolyte is used to separate the battery into two compartments of cathode and anode in the presence of a liquid electrolyte. During charge and discharge, the ions diffuse and migrate across the solid electrolyte and electrochemical reactions take place at the electrodes. Understanding the lithium-ion diffusion mechanism between the liquid electrolyte and the solid electrolyte is highly important for the improvement of such batteries’ performance. [ 20 , 21 ] The migration of ions across the interface between the liquid and solid electrolytes includes: (i) absorption of solvated ions on the surface of solid electrolyte, (ii) desolvation of lithium ions, (iii) hopping of lithium ions into the lattice of the solid electrolyte, and (iv) migration of lithium ions from the outer surface into the inner part of the solid electrolyte. The factors influencing the dynamic properties of lithium-ion diffusion in this model include: (i) absorption energy of solvated ions on the surface of solid electrolyte, (ii) desolvation energy, and (iii) surface structure of the solid electrolyte. [ 22 ] The thermodynamics of ion transport across the interface was investigated by Ogumi using a symmetric cell, and it was found that the desolvation process of ions had higher energy than the other processes. [ 20 , 22 , 23 ] The interaction between ions and solvent molecules affects the dynamics of ion migration across the interface. In high concentration propylene carbonate (PC) solution, a strong interaction exists between lithium ions and solvent molecules, making the desolvation process the rate-determining step.
Composite electrolytes of polymer and inorganic materials are very safe and flexible, and can be made compatible with existing battery structures and the means of fabrication. Therefore, composite solid electrolytes are very promising candidates for the next generation of solid-state batteries. [ 1 , 24 ] A polymer electrolyte was first reported in 1975 by Wright et al. [ 25 ] Later on, Wieczoreck found that conductivity was increased by adding inorganic particles into the polymer electrolyte. [ 26 ] The inorganic filler lowered the glass transition temperature and prevented crystallization of the polymer, leading to an increase in conductivity. [ 27 ] Scrosati proposed that ion diffusion at the interface also contributes to an increase in conductivity. [ 28 ] Interactions between functional groups on the surface of inorganic materials and those on the surface of polymers are shown in Fig.
 | Fig. 7. Diagram showing the interaction of polymer electrolyte and inorganic materials with different surface functional groups. [ 28 ] |
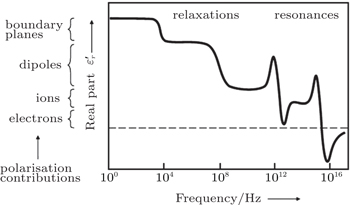
Ionic transport involves dynamic processes at different scales: the vibration at equilibrium positions, ion hopping between different equilibrium sites, long distance ionic transport in grain lattices and homo-structure polymers, as well as migration across or along the interface. In order to fully understand the transport of ions, different research tools are applied, as listed in Table
| Table 1. Research techniques for the study of ionic transport. [ 32 ] . |
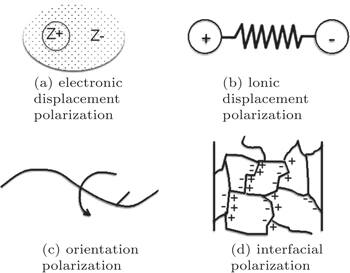
Several different polarization mechanisms are found in materials: electronic displacement polarization, ionic displacement polarization, orientation polarization, and interfacial polarization as shown in Fig.
The impedance properties of materials can be understood with the help of an equivalent circuit, which has the same impedance response. For example, a typical impedance spectrum of a ceramic electrolyte contains two responses, one from the grains and the other from the grain boundaries, as shown in Fig.
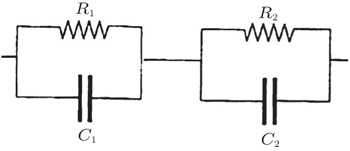 | Fig. 11. Equivalent circuit of an inorganic solid electrolyte. 1 and 2 represent different conductivity regions. |
Several different representations for impedance data, i.e., impedance, inductive, modulus, and permittivity, are shown in Table
 | Fig. 12. Nyquist plot of Z * (a), Nyquist plot of M * (b), and Bode plot of Z ″ and M ″ (c), for the equivalent circuit in Fig. |
 | Fig. 13. Nyquist plot of Z * (a), Nyquist plot of M * (b), and Bode plot of Z ″ and M ″ (c), for the equivalent circuit in Fig. |
| Table 2. Different representations for impedance data. μ = jωC c , where C c is the capacitance of an empty cell. . |
Nuclear magnetic resonance is a powerful experimental technique for studying diffusion. For non-ionic conductors, NMR shows a Gaussian distribution. For superionic conductors in which ions can transport in a long range by fast hopping through adjacent lattice sites, NMR gives a Lorentz distribution with a narrow width. [ 41 ] Heitjans investigated lithium diffusion in Li 2 O using NMR. When the crystal size of Li 2 O was decreased down to the nano-scale, the NMR spectrum showed a new narrow Lorentz-like peak, indicating that the ions at the interface of nano-scale polycrystalline Li 2 O had faster motion than the ions in the inner grains. [ 42 ] Similar phenomena were also observed in nano-scale LiNbO 3 , LiTiO 3 , and other materials. [ 43 , 44 ] For Li 2 O–Al 2 O 3 composite, NMR spectra suggested an overlap of Gaussian and Lorentz peaks, as shown in Fig.
 | Fig. 14. 7 Li NMR spectra ( ν = 58.3 MHz) at various temperatures of the (a) micro- and (b) nano-crystal composite 0.5Li 2 O·0.5Al 2 O 3 . [ 42 , 45 ] |
In addition to the effect on the width of NMR spectra, fast transport of ions in materials also influences the relaxation process, including spin–lattice relaxation ( T 1 ), spin–spin relaxation ( T 2 ), and spin–lattice relaxation in a rotating coordinate system ( T 1p ). [ 32 , 41 , 46 ] As shown in Fig.
 | Fig. 15. 7 Li nuclear magnetic resonance (NMR) free induction decays of nanocrystalline (1 – x )Li 2 O: x Al 2 O 3 composites recorded at 58.8 MHz at different temperatures ( T is temperature and x is Al 2 O 3 content). [ 45 ] |
In addition to IS and NMR, other techniques have also been used to gain an insight into interfacial diffusion. Computer simulations can predict the interfacial structures and ion diffusion dynamics of materials. Secondary ion mass spectrometry (SIMS) can provide spatial distribution of elements, and is a very useful tool to distinguish ion diffusion in grains and at interfaces. [ 47 ] Combining spatial scanning technology with electrical measurements can give a micro electrical structure of grain conductivity and interfacial conductivity, which is highly beneficial to research on interfacial diffusion. Zhu et al. investigated ion diffusion in LiCoO 2 polycrystalline films by conductive atomic force microscopy, revealing different electrical properties of grains and grain boundaries. [ 48 ]
So far, the research methods for ion diffusion have been limited. Development of new techniques is needed in order to better understand interfacial diffusion.
Compared with studies done on other physical processes in lithium-ion batteries, the research on interfacial diffusion is still in its infancy, which limits the development of the battery performance to a degree. In order to further improve lithium-ion batteries, several aspects of research related to interfacial transport should be pursued. These research topics include nanoionics, composite solid electrolytes and ionic transport in electrode layers.
The development of solid electrolytes is crucial to the next generation of very safe solid-state batteries. In addition to optimization of crystal structures, fast interfacial diffusion is another new direction for designing novel electrolyte materials. The concept “nanoionics” has been proposed. [ 49 , 50 ] When the particle size of a material with fast interfacial diffusion is nano-scale, the high volume percentage of the interface may increase the total conductivity of the material.
During decades of research on lithium-ion batteries, the structural evolution of cathode materials, ion diffusion in lattice, and electrochemical processes have been studied extensively. However, our knowledge of interfacial diffusion is insufficiently detailed, limiting the development of advanced battery technologies. To significantly improve batteries, high performance electrolytes with good overall properties, such as high conductivity, wide electrochemical window, good safety, great stability in a wide temperature range and good mechanical properties, are required. [ 51 , 52 ] Since including all the properties in one material is a big challenge, it is necessary to develop a composite electrolyte by combining different existing electrolytes – solids, polymers, and liquids. [ 53 , 54 ] As interfacial transport plays a major role in the diffusion of ions, understanding the physical mechanisms of ion diffusion at a multiphase interface will greatly help the designers of a new composite electrolyte.
High energy density is one of the most important requirements for commercial applications of batteries. [ 55 ] In order to improve the energy density and power density of batteries, the optimization of electrode structure is necessary. The constituents in electrodes include active materials, electronic conducting additives, binders, and penetrating liquid electrolytes. Electrode materials are secondary particles composed of small primary crystals. The active material particles of electrodes are combined with conducting additives. A binder binds together all the electrode particles and additive particles. Ion diffusion in the electrode layer is not only a multiple-phase transport process, but also a multiple-scale transport phenomenon, including ion hopping in the lattice of the electrode material, ion diffusion among the primary crystals, ion diffusion at the interfaces of different phases (electrode particles, polymer binder, conducting additives, liquid electrolyte), and ion diffusion along macro pathways from the bottom of the electrode layer to the surface. [ 56 ] Understanding the complex transport process in an electrode layer will dramatically help design new electrode structures so that rate performance can be improved, the amount of non-active materials can be reduced and ultimately the energy density of the full battery can be increased.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 |