† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant No. 2013CB934001) and the National Natural Science Foundation of China (Grant Nos. 51072012 and 51272015).
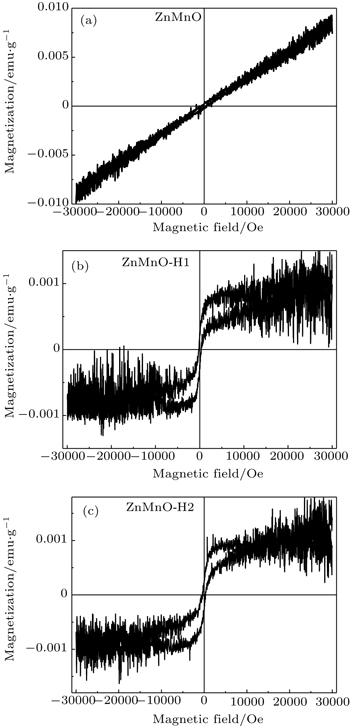
Mn-doped ZnO nanocrystals are synthesized by a wet chemical route and treated in H 2 /Ar atmosphere with different H 2 /Ar ratios. It is found that hydrogen annealing could change the coordination environment of Mn in ZnO lattice and manipulate the magnetic properties of Mn-doped ZnO. Mn ions initially enter into interstitial sites and a Mn 3+ O 6 octahedral coordination is produced in the prepared Mn-doped ZnO sample, in which the nearest neighbor Mn 3+ and O 2 ions could form a Mn 3+ –O 2− –Mn 3+ complex. After H 2 annealing, interstitial Mn ions can substitute for Zn to generate the Mn 2+ O 4 tetrahedral coordination in the nanocrystals, in which neighboring Mn 2+ ions and H atoms could form a Mn 2+ –O 2− –Mn 2+ complex and Mn–H–Mn bridge structure. The magnetic measurement of the as-prepared sample shows room temperature paramagnetic behavior due to the Mn 3+ –O 2− –Mn 3+ complex, while the annealed samples exhibit their ferromagnetism, which originates from the Mn–H–Mn bridge structure and the Mn–Mn exchange interaction in the Mn 2+ –O 2− –Mn 2+ complex.
Nowadays, semiconductor devices are a great challenge to data processing and storage capacity. Generally, this could be improved by simultaneously manipulating the spin and charge properties of electrons. Diluted magnetic semiconductor (DMS), a promising candidate for spin-polarized-current-injection material, [ 1 , 2 ] especially ZnO has recently attracted extensive attention. [ 3 , 4 ] Massive theoretical studies have been conducted and predicted that p-type Mn-doped ZnO could present ferromagnetic behavior at room temperature (RT). [ 5 – 7 ] Different magnetic properties in Mn-doped ZnO such as ferromagnetic, [ 8 , 9 ] paramagnetic, [ 10 , 11 ] or antiferromagnetic behavior [ 12 ] have been observed. Zheng et al. [ 12 ] showed that Mn-doped ZnO tetrapod structures have a Curie temperature T C = 43 K, which originates from (Zn, Mn) Mn 2 O 4 at the surface. Cheng and Chien [ 13 ] observed paramagnetic behavior caused by homogeneous distribution of Mn in epitaxial Mn-doped ZnO thin film. Inamdar et al. [ 14 ] found that incorporation of Mn 2+ ions at substitutional sites in perfect crystal produces a higher saturation magnetic moment than in the un-doped material. Through the above researches, we can draw a conclusion that the coordination environment of Mn in ZnO plays a key role in understanding the magnetic mechanism, and there is a fundamental relation between the observed ferromagnetism and substitutional Mn in the ZnO system. It is very important to investigate the coordination environment of Mn in order to clarify the origin of magnetism in the Mn-doped ZnO system.
The oxidation states and the local coordination of the selected atom, even in a diluted context, can be exactly studied by x-ray absorption fine structure spectroscopy (XAFS). [ 15 ] By analyzing the Mn and Zn K -edge XAFS spectra, Céspedes et al. [ 16 ] found that the ferromagnetism in Mn-doped ZnO originated from high-density regions of Mn cations with a MnO 2 – δ distorted environment at non-stoichiometric and highly defective ZnO grain boundaries. Zhang et al. [ 17 ] suggested that the Mn-doped ZnO system exhibited substantial paramagnetic behavior and the strong antiferromagnetism (AFM) demonstrated by the mere occupation of Zn sites with Mn ions, forming spin-antiparallel pairs and inducing a large structural distortion, which was confirmed by the XAFS spectra.
As is well known, hydrogen is inevitably introduced into the ZnO lattice and will form shallow donors. We have obtained that (Mn, N) co-doping can enhance the solubility of Mn in the ZnO lattice via reducing the donor binding energy of Mn impurity by orbital hybridization between the N-acceptor and Mn-donor. [ 18 ] We considered that the donor binding energy of the impurity should decrease if hybridization between H-donors and Mn-donors exists. In addition, some theoretical calculations and experimental results indicated that interstitial hydrogen can induce or enhance ferromagnetism in transition metal (TM) ion doped ZnO. [ 19 – 21 ] In a hydrogen annealed Mndoped ZnO system, the magnetic properties are different, and the source of the observed magnetism is still under intense debate. Manivannan et al. [ 22 ] noted that the magnetism of Mndoped ZnO is unchanged after hydrogenation. Sharma and Varma [ 23 ] proposed that the RT ferromagnetism in their hydrogenated sample is generated from oxygen vacancies and Zn interstitials. Our previous work [ 20 ] has stated that there is a great enhancement of ferromagnetism in hydrogen annealed Co-doped ZnO nanocrystal due to the formation of stable structure Co–H–Co. We supposed that similar structures could be observed by annealing Mn-doped ZnO in hydrogen, which may cause ferromagnetic coupling in the nanocrystal.
The aim of this work is to establish the relationship between the magnetic properties and the coordination environment of Mn in the ZnO lattice. In this work, we synthesize Mn-doped ZnO nanocrystals by the wet chemical route and treat them in H 2 /Ar atmosphere. The Mn coordination environment is investigated by XAFS. We demonstrate that hydrogen annealing can manipulate the coordination environment of Mn, thus inducing magnetic property variation in Mn-doped ZnO.
Mn-doped ZnO nanocrystals were synthesized by the wet chemical route as described previously. [ 18 ] The precursor salts (zinc acetate and manganese acetate) were dissolved in dimethyl sulfoxide (DMSO) according to the desired stoichiometry. The total metal ion concentration was 0.1 M. Tetramethylammonium hydroxide (TMAH) was dissolved in ethanol, keeping the concentration at 0.55 M. Then, the ethanol solution of TMAH was dropwise added into the metal salt solution with constant stirring at room temperature. After 48 h, the nanocrystals were precipitated by adding ethyl acetate and removed from the supernatant by centrifugation. Finally, the precipitates were annealed at 873 K in air for 3 h in order to remove the precursor. The obtained powders were annealed under H 2 /Ar atmospheres with different ratios of H 2 :Ar at 873 K for 2 h. The ratios of H 2 /Ar were 1:5 and 4:5, respectively. We denote the as-prepared and H 2 annealed samples as ZnMnO, ZnMnO-H1 (1:5), and ZnMnO-H2 (4:5), respectively.
X-ray diffraction (XRD) patterns were collected on a Rigaku Dmax/C x-ray diffractometer using Cu K α radiation operated at 40 kV and 200 mA. Mn K -edge x-ray absorption near edge structure (XANES) and extended x-ray absorption fine structure (EXAFS) spectra were collected in fluorescence mode due to the lower concentration of Mn on Beamline 1W1B at the Beijing Synchrotron Radiation Facility and Beamline BL14W on the Shanghai Synchrotron Radiation Facility. Raman spectra were collected on an HR800 LabRam Infinity spectrometer excited by a continuous Ar + laser with a wavelength of 514 nm. The magnetic measurements were carried out using a physical properties measurement system (PPMS; Quantum Design) equipped with a vibrating sample magnetometer.
Figure
Figure
 | Fig. 3. Normalized Mn K -edge XANES spectra of ZnMnO, ZnMnO-H1, ZnMnO-H2, and the reference samples of MnO, Mn 2 O 3 , and ZnO. |
Figure
Figure 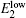
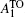


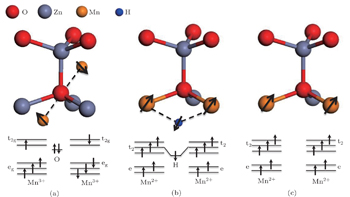
There are two main positions of Mn in the ZnO lattice after doping. One is interstitial, with the Mn ions forming the MnO 6 octahedral configuration as shown in Fig.

Here, the dielectric constant, ε , and the charge of the electron, e , are all constant. So E B only depends on the value of the Bohr radius of the donor, a d . In the as-prepared sample, the donor binding energy of the impurity is induced by Mn 3+ , in which there are four electrons in the d-shell. When the sample is annealed in hydrogen, H can offer an electron to the Mn 3+ ion and form a covalent bond with it. The hybridization between Mn and H would enhance the value of a d . According to Eq. (
Figures
| Table 1. Valence, main state of Mn in the ZnO lattice, the local coordination of Mn, and RT magnetic property in ZnMnO, ZnMnO-H1, and ZnMnO-H2. . |
We also measure M – H curves of ZnMnO-H1 and ZnMnO-H2 at 5 K after cooling from 350 K in 0 and 1000 Oe fields. The loops of zero-field cooling (ZFC) and field cooling (FC) hysteresis are shown in Figs.
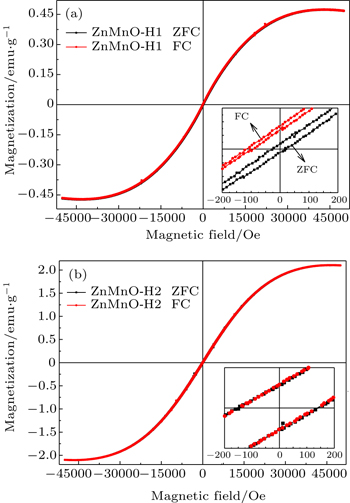 | Fig. 8. ZFC and FC (for 1000 Oe) M – H curves measured at 5 K for (a) ZnMnO-H1 and (b) ZnMnO-H2. The insets show the enlarged low-field regions of these two samples. |
Figures


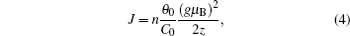
 | Fig. 9. (a)–(c) The M – T and 1/ χ – T curves of ZnMnO, ZnMnO-H1, and ZnMnO-H2 in a temperature ranging from 5 to 350 K in a magnetic field of 1000 Oe. |
There is other magnetic phase transition at about 250 K in both hydrogen annealed samples as displayed in Figs.
| Table 2. Values of θ 0 , C 0 , θ 0 / C 0 , n , and J . . |
In order to establish the relationship between the magnetic coupling and the coordination environment of Mn in the ZnO lattice, crystal lattice and energy level diagrams of a Mn 3+ O 6 octahedron at an interstitial site and a Mn 2+ O 4 tetrahedron at a substitutional site are given in Fig.
We synthesize Mn-doped ZnO nanocrystals by a wet chemical route and post hydrogen annealing. Our results indicate that Mn ions initially enter into interstitial sites in the ZnO lattice and form Mn 3+ O 6 groups with an octahedral coordination in the as-prepared sample. Hydrogen annealing can change the state of Mn into Mn 2+ O 4 , which has a tetrahedral coordination at the substitutional sites. Antiferromagnetism of as-prepared nanocrystals, originating from the interactions of the Mn 3+ –O 2− –Mn 3+ complex in the octahedral coordination, is obtained. The annealed sample exhibits ferromagnetic behavior due to the Mn–H–Mn bridge structure and Mn–Mn complex in the tetrahedral coordination. Our results suggest that the coordination environment of Mn can be changed with hydrogen annealing, which generates a significant effect on the magnetic properties of Mn-doped ZnO. The relationship between the magnetic coupling and Mn coordination environment will provide a new perspective for manipulating magnetic coupling mechanism in DMSs.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 |