† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 20990234, 20925414, and 91227121), the Program for Changjiang Scholars and Innovative Research Team in University, China (Grant No. IRT1257), the Programme of Introducing Talents of Discipline to Universities, China, and by the Tianhe No. 1, China.
Block copolymers are a class of soft matter that self-assemble to form ordered morphologies on the scale of nanometers, making them ideal materials for various applications. These applications directly depend on the shape and size of the self-assembled morphologies, and hence, a high degree of control over the self-assembly is desired. Grafting block copolymer chains onto a substrate to form copolymer brushes is a versatile method to fabricate functional surfaces. Such surfaces demonstrate a response to their environment, i.e., they change their surface topography in response to different external conditions. Furthermore, such surfaces may possess nanoscale patterns, which are important for some applications; however, such patterns may not form with spun-cast films under the same condition. In this review, we summarize the recent progress of the self-assembly of block copolymers grafted onto a flat substrate. We mainly concentrate on the self-assembled morphologies of end-grafted AB diblock copolymers, junction point-grafted AB diblock copolymers (i.e., Y-shaped brushes), and end-grafted ABA triblock copolymers. Special emphasis is placed on theoretical and simulation progress.
Block copolymers are a typical class of soft material that can self-assemble to form periodically ordered morphologies. The natural tendency to self-assemble makes block copolymers an ideal model system for the study of self-assembly of soft matter, and offers an efficient means of fabricating nano-scale structures. The resulting self-assembled structures can be used in various nanotechnology applications such as nanolithography, fabrication of nanoporous membranes for advanced separation media, photonic crystals, high-density media storage, biomineralization, drug delivery, colloidal stabilization, tailoring adhesion or wettability, and structure-directing agents for organic and inorganic materials with novel properties and functionalities. [ 1 – 13 ] These applications directly depend on the shape and size of the self-assembled structures, and hence, a high degree of control is required over the self-assembly process.
Grafting block copolymer chains onto a substrate to form copolymer brushes is a versatile method to fabricate functional surfaces. [ 14 – 20 ] Due to phase separation between the blocks, block copolymer brushes are commonly used to create smart surfaces. [ 21 ] In particular, the inclusion of a solvent can selectively expose one block of copolymer brushes. The combination of different polymeric blocks in a responsive thin film results in a broadening of the switching range of properties, so that the surface property of the film changes from the property of one polymer to that of the second polymer, or is locked in some intermediate state. [ 21 ] Therefore, such systems possess the reversibly tunable property of changing the surface topography in response to different external conditions. [ 14 – 24 ] These so-called smart surfaces hold great promise in various applications. [ 21 , 25 – 27 ] Furthermore, this simple yet very powerful method of tailoring surface topologies has led to exciting developments in using surface-grafted polymers as potential “soft vehicles” capable of moving nanosized objects. [ 28 , 29 ] Moreover, block copolymer brushes can lead to stable nanoscale-patterned surfaces, which may not form with spun-cast films under the same conditions due to the affinity of the substrate for one of the components. [ 30 ] The nanoscale-patterned surfaces are important for applications such as nanolithography.
From a broader point of view, grafted block copolymers are only one member of the big family of polymer brushes in which the grafted chains can be homopolymers, mixtures of homopolymers, random copolymers, block copolymers, or functionalized polymers. In these polymer brushes, the polymer chains are chemically grafted onto various surfaces through covalent bonds. Many aspects of various polymer brushes have been extensively reviewed in the literature. [ 31 – 36 ] Of special interest are brushes that consist of two or more immiscible components, because these systems exhibit phase separation on nanoscopic length scales. [ 19 – 23 , 37 , 38 ] Block copolymer brushes [ 14 – 18 , 30 , 39 ] and mixed homopolymer brushes [ 40 – 44 ] are two typical examples. Furthermore, the substrate of a polymer brush can be flat or curved (for example, spherical or cylindrical). Polymer brushes on flat substrates are the most frequently studied systems. In the current review, we summarize recent progress on the self-assembly of block copolymers grafted onto a flat substrate.
Over the past two decades, a large number of publications have appeared on self-assembly block copolymer brushes on a flat substrate. [ 14 – 23 , 30 , 39 , 45 – 85 ] Recently, binary polymer brushes (including mixed homopolymer brushes and diblock copolymer brushes) on curved substrates have also received much attention. Zhao and Zhu [ 31 ] have summarized the progress of the synthesis, responsive properties, self-assembled structures, and applications of mixed brush-grafted particles (i.e., curved substrates) with a spherical core radius R core significantly larger than, comparable to, or smaller than the root-mean-square end-to-end distance (〈 R rms 〉) of grafted polymers. In the case when the size of core particles is significantly larger than the 〈 R rms 〉 value of the grafted polymers, the influence of substrate curvature is almost ignored, and thus, the phase behavior of the mixed brushes on such large particles is close to that on flat substrates. More recently, Chen et al. [ 36 ] have summarized the theory and simulations related to binary polymer brushes, especially emphasizing the progress of binary polymer brush-grafted nanoparticles. This review also includes the recent progress of binary polymer brushes grafted to flat substrates as well as curved ones. These reviews [ 31 , 36 ] and the original works cited therein have demonstrated that the curvature of the particles plays an important role in determining the phase structures of binary brushes in cases when the R core is comparable to or smaller than the 〈 R rms 〉 value of the grafted polymers.
A detailed understanding of the microphase separation in the brush system is of fundamental importance to permit substantial progress with applications making use of the environmentally responsive properties of surfaces, as well as those based on nanoscale surface patterns. Furthermore, understanding the mechanism of structural formation in these brush systems would open some exciting possibilities to create structured surfaces with controllable responsive properties or with nanoscale patterns. Theories and computer simulations provide powerful tools to study the phase behavior of block copolymer brushes at the microscopic level. In particular, simulations can provide straightforward morphological information of copolymer brushes from a molecular viewpoint. In this review we will mainly concentrate on the self-assembled morphologies of grafted AB diblock copolymers and ABA triblock copolymers, especially emphasizing the theoretical and simulation progress. Various theoretical and simulation methods have been used in identifying the surface morphology of grafted block copolymers. The readers are referred to the recent review, [ 36 ] and related papers, where some theoretical and simulation methods have been reviewed in detail.
A large amount of research over the past two decades has provided a solid foundation for understanding the self-assembly of block copolymers in the bulk phase. The resulting structure is dictated by a balance between enthalpic interactions, which tend to minimize A/B contacts, and entropic contributions, which aim to minimize the distortion of the molecular conformations. For the simplest block copolymer system, i.e., an AB diblock copolymer melt, the phase diagram is mainly controlled by the degree of segregation, quantified by the product χ N , (where χ is the Flory–Huggins interaction parameter, and N the degree of polymerization) and the volume fraction of the A-block, f A . [ 86 – 89 ] Ordered equilibrium phases, including lamellae, hexagonally packed cylinders, body-centered-cubic spheres, and a bicontinuous network structure gyroid phase, have been identified in diblock copolymer melts. It has been illustrated that ABA type symmetric triblock copolymer melts, in which there are two identical end A-blocks covalently bonded to the middle B-block, exhibit very similar phase behavior to AB diblock copolymers formed by cutting the triblock copolymer in half. [ 90 , 91 ]
Qualitatively, the physical principles that underpin microphase separation of block copolymers in the bulk phase and structural formation of grafted block copolymers are similar. [ 30 ] Therefore, it can be assumed that a grafted block copolymer system has the tendency to form morphologies similar to those of the bulk phase. However, the polymer chains are covalently attached to a solid substrate, which imposes constraints on the grafted blocks, thus preventing them from forming a bulk phase. The interplay of these two tendencies, as well as the substrate properties and the affinity of the segments for the air surface, is expected to induce a large variety of surface morphologies.
Besides the intrinsic parameters (monomer–monomer interactions, block compositions, monomer–substrate interactions, and monomer–air interactions) and the constraints imposed on the grafting points, the phase behavior of grafted block copolymers is controlled by a number of factors. The grafting density is an important parameter that determines the physical properties of a polymer brush. It is defined by σ = 1/ d 2 , where d is the distance between adjacent grafting points. The presence and quality of a solvent can greatly influence the polymer conformation, and therefore greatly influence the surface morphology of the brush. Other factors such as the particular point at which the macromolecule is grafted, the molecular architecture of the polymer, and the distribution of the grafting sites on the substrate can also have a great influence on the surface morphologies of grafted block copolymers.
In block copolymer brushes, diblock (or triblock) copolymers are usually grafted to a solid substrate by one end of the polymer, called end-grafted diblock (or triblock) copolymers. For the end-grafted diblock copolymers, [ 30 , 39 , 45 – 67 ] there is a natural asymmetry in the distribution of segments perpendicular to the grafting substrate; that is, the grafted blocks have to be in contact with the substrate, whereas the upper blocks do not necessarily have to be in contact with the substrate. This natural asymmetry between the two blocks results in a perpendicular segregation tendency and this tendency is enhanced by incompatibility of the two blocks because the segregation decreases the number of unfavorable A/B contacts. On the other hand, lateral segregation does occur under some conditions. [ 53 , 62 , 64 ] A specific case of diblock copolymer brushes is represented by Y-shaped or V-shaped brushes when Y-shaped AB copolymers are grafted onto a flat surface by the “stem”. [ 68 – 80 ] One “arm” of the Y-shaped brush is an A homopolymer, and the other arm is an incompatible B chain, and the short “stem” tethers the entire copolymer to the surface. The Y-shaped brush also can be considered as diblock copolymers are grafted onto a surface through the junction points. In the Y-shaped brush case, the natural asymmetry mentioned above for end-grafted diblock copolymers does not exist. In this case, lateral segregation is the major form. [ 79 , 80 ] Therefore, the morphology of block copolymer brushes greatly depends on the particular points at which the macromolecule is grafted. We will provide a brief review on main features of morphologies obtained from end-grafted AB diblock copolymers and Y-shaped AB copolymer brushes in Sections 2 and 3, respectively.
A number of studies [ 47 , 81 – 85 ] have been carried out on ABA triblock copolymer brushes, though they are much less widely studied than AB diblock copolymer brushes. The grafted ABA triblock copolymers may exhibit a folded brush structure where the two end blocks aggregate together and force the middle blocks to the solvent interface. This structure is formed due to the molecular architecture of ABA triblock copolymers. We will provide a brief review on the main features of morphologies obtained from end-grafted ABA triblock copolymers in Section 4. Finally, we will conclude with a brief comment on the open questions in the study of grafted block copolymers in Section 5.
For end-grafted diblock copolymers, melt brushes should be the simplest case. Using self-consistent field theory (SCFT), Matsen and Griffiths [ 30 ] investigated the morphologies formed by a melt brush of AB diblock copolymers grafted to a flat substrate by their B ends. For simplicity, their study assumed a sufficiently high grafting density to permit the ignorance of substrate interactions that might otherwise pin the A-rich domains to the substrate. They found that the behavior of the grafted films was controlled by four quantities: the usual diblock copolymer parameters of segregation, χN , and A-block volume fraction, f (= f A ), plus the film thickness relative to the natural polymer size, L / aN 1/2 (where L is the film thickness), and the affinity of A segments for the air surface, ΛN . In addition to a laterally uniform morphology (uniform, Fig.
 | Fig. 1. Equilibrium morphologies calculated for four different diblock compositions, f , with χN = 40, ΛN = 0, and L / aN 1/2 = 0.5. Each image displays a lateral area of 3 aN 1/2 × 3 aN 1/2 . [ 30 ] (a) Uniform, f = 0.45, (b) hex I , f = 0.35, (c) stripe, f = 0.25, (d) hex, f = 0.15. Reprinted with kind permission from Springer Science+Business Media: 〈 Eur. Phys. J. E , Melt brushes of diblock copolymer, |
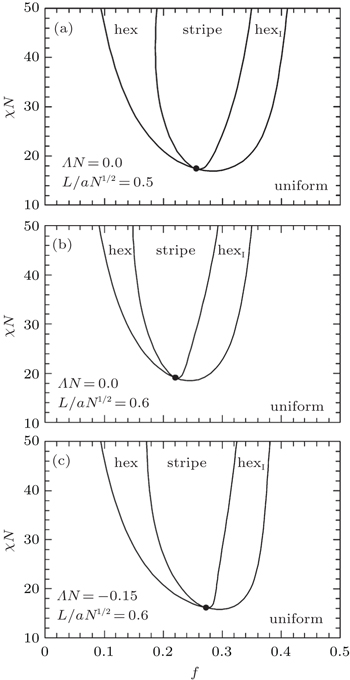 | Fig. 2. Equilibrium phase diagrams calculated for (a) ΛN = 0 and L / aN 1/2 = 0.5, (b) ΛN = 0 and L / aN 1/2 = 0.6, and (c) ΛN = − 0.15 and L / aN 1/2 = 0.6. [ 30 ] The dots denote mean-field critical points. Reprinted with kind permission from Springer Science+Business Media: 〈 Eur. Phys. J. E , Melt brushes of diblock copolymer, |
The SCFT calculation also predicted that the region of periodic morphologies in the phase diagram increased in size as the air surface acquired a preference for the grafted B blocks (Fig.
To test the above theoretical calculations, O’Driscoll et al. [ 45 ] investigated grafted films of polystyrene-block-poly(methyl methacrylate) copolymers of varying composition and molecular weight using atomic force microscopy and compared the observed structures with theoretical predictions of Matsen and Griffiths. [ 30 ] They observed that the phase present in the films changed from disordered/uniform, to hexagonal, to inverse hexagonal and finally to uniform again as the fraction of the upper block increased, [ 45 ] which was in qualitative agreement with the theory. They also observed the predicted stripe phase in small areas in some of the samples. [ 45 ] Quantitatively, they found that their results were markedly different from those predicted by the theory. [ 30 ] They assumed that the observed phase behavior was influenced by residual solvent in the films prior to, and during, the second annealing process. [ 45 ] Their assumption was supported by their further calculations on the tethered block copolymer system with included solvent, indicating that the presence of a solvent, or the solvent treatment of a sample, may induce large differences in the resulting morphology of a brush. [ 45 ]
Besides melt brushes, systems of grafted diblock copolymers immersed in a solvent have attracted tremendous scientific attention. The inclusion of a solvent can selectively expose one block of the copolymer brushes, resulting in changes to surface patterns. These patterns may possess some unique stimuli-responsive properties and are switchable between the different morphologies with simple solvent treatments.
There is a large amount of experimental literature on this topic. Zhao et al. [ 39 , 46 ] showed for the first time, using contact angle measurements and atomic force microscopy (AFM), that selective swelling and collapse of poly(styrene-b-methyl methacrylate) (PS-b-PMMA) and poly(styrene-b-methyl acrylate) (PS-b-PMA) brush blocks produced variable and switchable surface topologies. They found that the brush morphologies ranged from smooth to very rough surfaces, with either regular structure or unusual morphology, depending on the environment the brush had been exposed to. They observed that the PS-b-PMMA and PS-b-PMA brushes exhibited different morphologies after treatment with CH 2 Cl 2 , and attributed this difference to the larger Flory–Huggins interaction parameter between PS and PMA as opposed to PS and PMMA. Using a combination of reverse atom transfer radical polymerization (RATRP) and standard ATRP techniques, Boyes et al. [ 47 ] synthesized AB diblock copolymer brushes and ABA triblock copolymer brushes. They found that these brushes have the ability to reversibly rearrange upon treatment with selective solvents. This rearrangement of block copolymer brushes can result in the formation of unusual surface morphologies that have been attributed to the formation of either “pinned micelles” or “folded” structures. They demonstrated that other external stimuli besides block-selective solvents, namely temperature and treatment with supercritical CO 2 , can be used to induce brush reorganization. Application of selectively swollen/collapsed copolymer brushes requires knowledge of how the development of the topographical features depends on the lengths of the individual blocks and the degree of collapse. Xu et al. [ 16 ] proposed an efficient and systematic method to allow the study of the influence of individual block length on the solvent response behavior of poly(n-butyl methacrylate)-b-poly(2-(N,N′-dimethylamino)ethyl methacrylate) (PBMA-b-PDMAEMA) brushes using tailored brush systems. Their results indicated that the solvent responsive behavior of the block copolymer brushes was greatly influenced by the relative block lengths. While surface responsive properties can be suppressed by a long top block, they can be enhanced by the extension of the bottom block. Tomlinson and Genzer [ 48 , 49 ] presented methodologies for fabricating block copolymer assemblies grafted onto flat solid substrates, where each block of the copolymer possessed a systematic and gradual variation of molecular weight as a function of the position on the substrate. They generated surface-tethered poly((2-hydroxyethyl methacrylate)-b-(methylmethacrylate)) (PHEMA-b-PMMA) diblock copolymer brushes and studied systematically morphological transitions associated with collapsing either the top PMMA or the bottom PHEMA block while keeping the other block solvated. Their scanning force microscopy studies of systems with the top block collapsed revealed the presence of either flat (F), or micellar (M) or bicontinuous (BC) morphologies, whose locus in the phase diagram agrees with theoretical predictions [ 50 – 52 ] and computer simulation results. [ 53 ] Using the same technique, Tomlinson and Genzer [ 49 ] also studied the formation of poly[(2-hydroxyethylmethacrylate)-b-(methyl methacrylate)-b-(dimethylaminoethyl methacrylate)] triblock copolymer brushes with independent variation of all three block lengths. Kong et al. [ 54 ] found that the solvent treatments can affect surface morphologies as well. Gao et al. [ 55 ] observed that by varying the upper block layer thickness, the self-assembly of grafted poly(oligo(ethylene glycol) methacrylate)-b-poly(methyl methacrylate) (POEGMA-b-PMMA) brushes resulted in various surface nanopatterns, including spherical aggregates, wormlike aggregates, line patterns, perforated layers and complete overlayers. Their observations agreed with results of computer simulations. [ 53 ] They observed that the smallest feature size was less than 10 nm. Gao et al. [ 18 ] also prepared nanoscale patterns by self-assembly of block copolymer brushes to pattern biomolecules for potential biological and medical applications. O’Driscoll et al. [ 56 ] have examined the behavior of a number of grafted PS-b-PMMA diblock copolymer films and observed dependencies on both the annealing time and the nature of the solvent used to wash the films. Yu et al. [ 57 ] synthesized poly(N-isopropylacrylamide)-b-polystyrene (PNIPAM-b-PS) brushes with the aim of combining the thermal sensitivity of PNIPAM and the hydrophobic characteristics conferred by the PS blocks in order to create surfaces responsive to both temperature and solvent. In a recent study, Jalili et al. [ 58 ] successfully prepared high grafting density, ultrathin, thermo-responsive poly(2-hydroxyethyl methacrylate)-b-poly(N-isopropylacrylamide) (PHEMA-b-PNIPAM) diblock copolymer brushes with tunable wettability under carefully controlled conditions on the surface of silicone rubber by the surface-initiated atom transfer radical polymerization technique to trace the thermally induced phase transition mechanisms in water. They observed that upon exposure to higher-temperature conditions (above the LCST of the PNIPAM top block), the film showed a “matrix-island” structure, in which the PNIPAM nanodomains were distributed over the highly packed PHEMA bottom block. All of these studies showed that the self-assembly of block copolymer brushes represented a promising approach for the preparation of surfaces with nanoscale patterns and switchable topologies.
The first theoretical study of end-grafted diblock copolymers in solution was carried out by Zhulina et al. [ 50 – 52 ] They employed a two-dimensional lattice SCFT to identify morphologies and scaling arguments to outline the general phase behavior for a system with relatively low densities. It has been predicted that the copolymer brushes in a selective solvent exhibit several distinct morphologies: the regime of nonaggregating chains (I), A-legged micelles (MAB), pure B pinned micelles (PMB), the star-like block copolymer micelles (MA), and a bicontinuous phase (BAB). [ 51 ] The morphological sequence from I to MAB or PMB and then to BAB was predicted with the increase of the top block length. The morphological sequence from PMB to MAB and then to MA was predicted with the increase of the grafted block length. [ 51 ] It has also been predicted that in a poor solvent for both components, by controlling the chain architecture, grafting density, molecular lengths of the copolymer and its individual components, interaction energy between different blocks, and interaction energies between blocks and solvents, one can design patterned polymer films forming a series of well-defined novel structures such as “onion”, “garlic”, “dumbbell”, “flower-like”, and “checkerboard”. [ 50 ] Using a one-dimensional continuum SCFT calculation, Ferreira and Leibler [ 59 ] studied the microstructure of diblock copolymer brushes in an implicit good nonselective solvent. A demixing transition was found for the diblock copolymer brushes when the Flory–Huggins interaction parameter χ is positive and solvent is poor. For a negative χ , the A and B blocks were attracted to each other. Thus the B segment can enter the A block region near the surface and the copolymer brushes become less stretched. Also using a one-dimensional continuum SCFT calculation, Meng and Wang [ 60 ] quantified the explicit solvent response of diblock polymer brushes by the changes of surface-layer composition and brush height. The influence of different parameters such as block fraction, block chain length, grafting density, incompatibility between two blocks, and solvent selectivity on the solvent response of diblock copolymer brush was also investigated. Using classical density functional theory calculations, Gong et al. [ 61 ] studied the phase behavior of AB diblock copolymer brushes in a selective solvent that prefers the A block to the B block. With increasing B-block length, they found structural transitions of the copolymer brush from mixed to collapsed, partially exposed, and exposed structure, which were attributed to the interplay between the entropic cost of folding copolymer brushes and the enthalpic effect of contact between unlike components. In addition, they examined the effect of different parameters on the solvent response of copolymer brushes, and found that the transition chain length increases when decreasing the grafting density and the bottom block length, and the collapsed structure becomes less stable when decreasing the chain length of solvent.
With regards to simulations, the majority of studied systems are in the presence of a selective solvent that is a good solvent for one block and a poor solvent for the other block. [ 53 , 62 ] Yin et al. [ 53 ] studied the phase behavior of diblock copolymer brushes in selective solvents using simulated annealing methods. Wang and Müller [ 62 ] performed a single-chain-in-mean-field (SCMF) simulation of a coarse-grained model to investigate the microphase separation of diblock copolymer brushes in implicit selective solvents. The morphological dependencies of the brushes on solvent selectivity, polymer grafting density, and block lengths were investigated systematically. Phase diagrams of the system were constructed, and complicated structures formed by perpendicular or lateral segregation (or their combination) were predicted in both studies. [ 53 , 62 ] In the simulated annealing study, in the case when the solvent was selective to the A-blocks (grafted blocks), morphological transitions of the B-blocks (top blocks), such as from a ripple structure to a wormlike structure and then to a spherical structure, or from a perforated layer structure to a ripple structure, or from a layer to a perforated layer structure, all dependent on the length of the B-blocks, were predicted with increasing the length of the A-blocks at a high grafting density. Similar morphological transitions were also predicted with decreasing the length of the B-blocks (Fig.
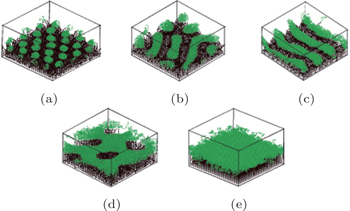 | Fig. 3. Morphologies of AB diblock copolymer brushes in a solvent that is selective to the grafted A-blocks for different lengths of the B-block with a high grafting density of σ = 0.25 and N A = 10: (a) spherical micelles, N B = 4; (b) wormlike micelles, N B = 8; (c) stripe structure, N B = 10; (d) perforated layer, N B = 16; (e) layer, N B = 20. Color scheme: A, black, B, green. [ 53 ] Reprinted with permission from Yin Y, Sun P, Li B, Chen T, Jin Q, Ding D and Shi A C 2007 Macromolecules |
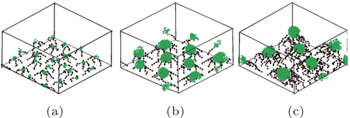 | Fig. 4. Morphologies of AB diblock copolymer brushes in a solvent that is selective to the grafted A-blocks for different lengths of the B-block with a low grafting density σ = 0.028: (a) N A = 4, N B = 4; (b) N A = 4, N B = 24; (c) N A = 10, N B = 24. Color scheme: A, black, B, green. [ 53 ] Reprinted with permission from Yin Y, Sun P, Li B, Chen T, Jin Q, Ding D and Shi A C 2007 Macromolecules |
 | Fig. 5. Illustration of morphologies of AB diblock brushes in a solvent that is a good solvent for the A block and a poor solvent for the B block, for the grafting density 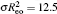  |
Studies of end-grafted diblock copolymers in the presence of a neutral or a poor solvent for both blocks were also carried out in simulations. The latter case is more closely related to melt brushes. Using Monte Carlo simulations, Romiszowski and Sikorski [ 65 ] analyzed the structure of end-grafted diblock copolymer brushes immersed in an implicit solvent whose quality was characterized by the reduced temperature T . They found that the spatial distribution along the z-axis of segments in the brush depended on T . Wang and Müller [ 62 ] found that in the case of a poor solvent for both blocks but with a small preference for one of the two blocks, the stability region of the laterally structured phases expands with decreasing grafting density, consistent with that obtained in the melt brushes. [ 30 ] Wang and Müller [ 63 ] also concluded that the morphology in a poor solvent was more susceptible to density fluctuations (or changes of density) than the brush in the other solvents. Using a coarse-grained dissipative particle dynamics simulation, Rudov et al. [ 66 ] studied the morphologies in dense planar brushes of diblock copolymers immersed in nonselective good or poor solvents for both blocks. They found that depending on the composition of the copolymer, various structures including hexagonally ordered “golf holes”, parallel “gullies”, “ridges”, and “stalactites” can be stable. Those structures have not been predicted or observed in other studies. A major difference in models from Rudov et al. [ 66 ] to others was that in their model, the attached end-beads of the A blocks can freely migrate in the x – y plane, and can detach from the wall but that detachment is accompanied by a penalty in the energy of the system. Using simulated annealing, Jiang et al. [ 67 ] studied the self-assembled morphologies of linear AB diblock copolymers grafted to a flat substrate by the ends of the A blocks and immersed in a solvent that was poor for both A and B components but exhibited a slight preference for one of the blocks. Phase diagrams for systems with two different grafting densities were constructed. They found that at a moderate grafting density, a variety of complicated morphologies (Fig.
 | Fig. 6. Morphologies of AB diblock copolymer brushes in a solvent that is poor for both A and B components but exhibits a slight preference for the A (grafted) blocks for different length of the A-block with N A = 8; (c) B wormlike micelles in A perforated layer with N A = 12; (d) B spheres in A perforated layer with N A = 14; (e) B spherical micelles in A complete layer with N A = 18. [ 67 ] Reprinted with permission from Jiang R, Li B, Wang Z, Yin Y and Shi A C 2012 Macromolecules |
When AB diblock copolymers are grafted onto a flat surface through their junction points, they form the Y-shaped (or V-shaped) AB brush, with one arm composed of A-polymer, and another arm composed of B-polymer. The Y-shaped AB brush can be viewed as a bridge between an end-grafted diblock copolymer brush and a mixed A and B homopolymer brush. The main advantages of the Y-shaped AB brush over the mixed A and B homopolymer brush are the homogenous distribution of both incompatible polymer chains over the complete surface, and the suppression of segregation processes. On the other hand, Y-shaped copolymer brushes can also be regarded as star ABC block copolymers with the C-arms grafted onto a substrate, i.e., end-grafted star ABC block copolymers. When the length of grafted C-arm is relatively short, the Y-shaped brush is reduced to a V-shaped AB brush. In this review we only consider the cases of Y-shaped brushes with relatively short C-arms or V-shaped AB brushes, and we do not distinguish between them.
Since the first synthesis of Y-shaped AB polymer brushes, [ 68 , 69 ] their self-assembly behavior has been studied by a great number of research groups. Experimentally, Julthongpiput et al. [ 68 , 70 ] studied Y-shaped copolymer brushes with two highly incompatible polystyrene (PS) and poly(acrylic) (PAA) arms. Novel surface structures of segregated pinned micelles and crater-like micelles were observed to form by these Y-shaped copolymers in different selective solvents. They also observed that the arms of the Y-shaped copolymers are capable of local reversible changes, leading to a reversible structural surface reorganization in different solvents. Zhao et al. [ 71 ] studied the molecular weight dependence of solvent-induced self-assembly of Y-shaped (which they called mixed) PMMA/PS brushes on silicon wafers. They observed a transition in water advancing contact angle ( θ a ) from 74° to 91° for a series of brushes with a fixed PMMA M n and systematically increasing PS M n , after treatment with CHCl 3 . They found that the brushes with PS M n slightly smaller than that of PMMA underwent self-reorganization in cyclohexane and exhibited different surface wettabilities. However, no significant changes in surface morphologies were found. They observed relatively ordered nanoscale domains in the brushes with PS M n slightly lower than or similar to that of PMMA after treatment with glacial acetic acid, a selective solvent for PMMA. Later, Lin et al. [ 72 ] and LeMieux et al. [ 73 ] characterized the surface morphology and nanomechanical and microtribological properties of the same Y-shaped copolymer brushes in different solvents by direct in-fluid observation. They observed the surface morphology of pinned micelles, and they also predicted similar morphology based on molecular modeling. Wang et al. [ 74 ] synthesized grafted polystyrene-block-poly(2-vinylpyridine) (PS-b-P2VP) copolymer Y-shaped brush and investigated the switchable behavior of the brush thin-film surface in selective solvents. They observed changes in the surface properties and morphology upon reduction of the miscibility of the two arms by methyl iodide reaction with the P2VP block to produce quaternary ammonium groups. Wang et al. [ 75 ] prepared V-shaped polymer brushes using amphiphilic polystyrene-poly(ethylene oxide) (PS-b-PEO) block copolymers bearing a trithiocarbonate group as the junction grafted on to a planar gold surface. They found that the morphology of the V-shaped PS-PEO brushes varies with the composition of the block copolymers and was responsive to solvent treatment. Tonhauser et al. [ 76 ] demonstrated a general concept for the preparation of junction-point-reactive, amphiphilic Y-shaped block copolymer brushes for ultrathin polymer films by combining anionic polymerization techniques. They found that the polymer films (1–3 nm) exhibited reversible, stimuli-responsive wetting behavior upon application of different external stimuli such as temperature and solvent.
Using scaling arguments, Zhulina et al. [ 77 ] investigated the behavior of grafted Y-shaped polymers in melt brushes and in the presence of solvents. These authors found that the grafted Y-shaped copolymers can form rich well-defined structures depending on the nonselective solvent quality, grafting density, and incompatibility between the two blocks. The phase diagram, constructed for the case of a nonselective poor solvent, contains regions of brushes and pinned micelles, which were dependent on the incompatibility between the two arms and the grafting density. [ 77 ]
Santer et al. [ 78 ] investigated the correlation between the morphology of both mixed and Y-shaped polymer brushes and fluctuations of the grafting points using SCMF simulations and atomic force microscopy experiments. They found that Y-shaped brushes exhibited a significantly weaker domain memory than conventional PS-PMMA mixed brushes, though the microphase-separated morphology was similar in both cases. This was because fluctuations in the composition of the grafting points of Y-shaped brushes were eliminated. They also found that in the mixed brush case, statistical fluctuations of the chemical composition occurred on a local scale whereas such composition fluctuations were strongly suppressed in the Y-shaped brush case. Their results indicated that Y-shaped mixed brushes were particularly promising candidates for pursuing applications based on the ability to relocate nano-objects following morphology switching. [ 78 ] The self-assembled morphologies of grafted Y-shaped copolymers in solution were investigated using simulated annealing techniques [ 79 ] and DPD simulations. [ 80 ] Both of these simulations systematically examined the influence of the solvent quality, the grafting density, and the incompatibility between the polymer blocks on the morphology of the grafted layer. The simulations clearly showed that the grafted Y-shaped block copolymers can form a rich variety of well-defined structures and present multiple morphological transitions in both nonselective and selective solvents. [ 79 ] When the solvent was nonselective and poor for the two arms, morphological transitions from mixed micelles to internally segregated micelles, to hamburger-like micelles, to segmented worm-like micelles, to connected micelles, and to split micelles were predicted with increasing A–B interaction, ε AB , at low grafting density. At high grafting density, morphological transitions from laterally homogeneous brush, to laterally segregated brush, and to solvent sandwiched brush were predicted. When the solvent was nonselective and good for the two arms, mixed and laterally segregated stretched brushes were obtained with increasing ε AB at both dense and sparse grafting. [ 79 ] When the solvent was selective for one of the two blocks, the resulting morphology could be perpendicularly segregated in addition to being laterally segregated, and was capable of reversible switching. When the solvent was selective and poor for both of the arms, morphological transitions from core-shell micelles to internally segregated micelles, to hamburger-like micelles, to segmented worm-like micelles, to connected micelles, and to split micelles (Fig.
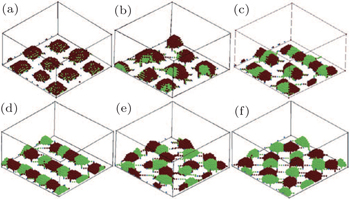 | Fig. 7. Morphologies of grafted Y-shaped copolymers in selective poor solvents at a low grafting density σ = 0.028: (a) core-shell micelles with ε AB = 0, (b) internally segregated micelles (or partially A-covered micelles) with ε AB = 0.9; (c) hamburger-like micelles with ε AB = 1.5; (d) segmented worm-like micelles with ε AB = 1.6; (e) connected micelles with ε AB = 2.0; and (f) split micelles with ε AB = 3.0. [ 79 ] Reprinted with permission from Yin Y, Jiang R, Li B, Jin Q, Ding D and Shi A C 2008 J. Chem. Phys. |
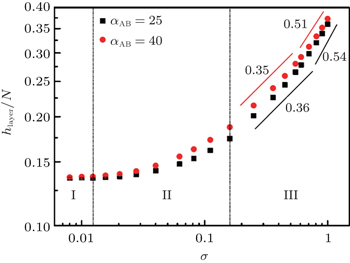 | Fig. 8. Log–log plots of the layer thickness h layer , normalized by the total chain length N = N A + N B , as a function of the grafting density for different A–B interaction parameters, α AB , with the polymer–solvent interactions parameter α PS = 25 (good solvent condition). [ 80 ] Reprinted with permission from Gao H M, Liu H, Lu Z Y, Sun Z Y and An L J 2013 J. Chem. Phys. |
In contrast to the AB diblock copolymer brushes, only a few studies have been published on ABA triblock copolymer brushes. Analogously to diblock copolymer brushes, studies have demonstrated that when treated with block-selective solvents, the grafted ABA triblock copolymer brushes are also capable of stimuli-responsive wetting, as they permit reversible switching of surface properties from hydrophilic to hydrophobic. On the other hand, brush morphologies formed by the former can be quite different from those formed by the latter, although symmetric ABA triblock copolymers, in which there are two identical end A-blocks covalently bonded to the middle B-block, have been identified as having very similar phase behavior with their analogous AB diblock copolymer in melt brushes. A pronounced difference is that ABA triblock copolymer brushes can form a folded brush structure.
Boyes et al. [ 81 ] showed the first experimental study of ABA triblock copolymer brushes composed of polystyrene-poly(methyl acrylate)-b-polystyrene (PS-b-PMA-b-PS) and PMA-b-PS-b-PMA. They observed that upon treatment with different solvents, the tethered triblock copolymer brushes exhibited reversible changes in surface properties. Furthermore, they observed that both triblock copolymer brushes exhibited nanomorphology after treatment with a good solvent for the middle block and nonsolvent for the grafted and end blocks. The formation of the unusual nanomorphology was attributed to migration of the outer block from the solvent interface and formation of aggregates with both neighboring outer blocks and grafted blocks to avoid contact with the solvent, whereas the middle block migrated to the solvent interface to form a shield around the aggregates formed by the outer and grafted blocks. [ 81 ] The unusual nanomorphologies were further attributed to the formation of either pinned micelles or folded structures. [ 47 ] Huang et al. [ 82 ] investigated the formation of poly(methyl methacrylate)-b-poly(dimethylamino ethyl methacrylate)-b-poly(methyl methacrylate) (PMMA-b-PDAEMA-b-PMMA) and poly(methyl acrylate)-b-poly(methylmethacrylate)-b-poly(hydroxyethyl methacrylate) (PMA-b-PMMA-b-PHEMA) brushes and phase segregation by these materials upon exposure to a poor solvent for the outer block. The systems they considered have greater differences in hydrophobicity between blocks than the PMA-b-PS-b-PMA brushes studied by Boyes et al. [ 81 ] When treated with selective solvents, the grafted triblock copolymer brushes exhibited similar changes to those in PMA-b-PS-b-PMA triblock copolymer brushes with regards to surface morphology, i.e., the grafted PMMA-b-PDAEMA-b-PMMA triblock copolymers do form segregated surface domains when exposed to a solvent selective to the middle PDAEMA blocks. However, because the hydrophobicity of PMMA is different from that of PMA, domains were relatively larger and more regular in the PMMA-b-PDMAEMA-b-PMMA case than those in PMA-b-PS-b-PMA case. [ 82 ] In addition, Rakhmatullina et al. [ 83 ] synthesized gold-supported amphiphilic triblock copolymer brushes composed of two hydrophilic poly(2-hydroxyethyl methacrylate) (PHEMA) blocks and a hydrophobic poly(n-butyl methacrylate) (PBMA) middle part, and they tested the solvent-responsive behavior of the brush using block-selective solvents as well as a good common solvent for both block types. They found that amphiphilic character of the triblock copolymer brushes provided a responsive surface that showed a solvent-dependent arrangement of the block copolymer chains, and suggested that the polymer brushes with a hydrophilic–hydrophobic–hydrophilic sequence can be regarded as solid-supported, biomimetic block copolymer membranes. [ 83 ]
Using a simulated annealing method, Xu et al. systematically investigated the morphologies formed by symmetric [ 84 ] and asymmetric [ 85 ] ABA triblock copolymers grafted to a flat substrate by one of their A ends, and immersed in a solvent selective for the middle B-blocks. Phase diagrams as a function of the block lengths for systems with different grafting densities have been constructed. Two types of brush structures were identified: structures with only one A-rich layer and structures with two A-rich layers. They found that structures with only one A-rich layer result from a folded brush structure in which all the triblock copolymer chains adopt a hairpin-like folded conformation to avoid the unfavorable contact of A-monomers with solvents. [ 84 , 85 ] The formation of such structures is consistent with the hypotheses from the experimental studies of ABA triblock copolymer brushes. [ 47 , 81 ] A variety of morphologies such as semispherical pinned micelles, worm-like micelles, stripe structures, connected stripe structures, perforated layered structures, semi-spheres-spheres, worm-like micelles-spheres, and stripes-spheres were observed for both grafted symmetric [ 84 ] and asymmetric [ 85 ] ABA triblock copolymers. For a grafted symmetric ABA triblock copolymer system, [ 84 ] morphological transitions from structures with only one A-rich layer to structures with two A-rich layers may be induced by increasing the length of the middle soluble B-block. Furthermore, the boundary between the two types of structures depends on the grafting density of the copolymers, and it moves to a smaller value of B length with the increase of the grafting density (Fig.
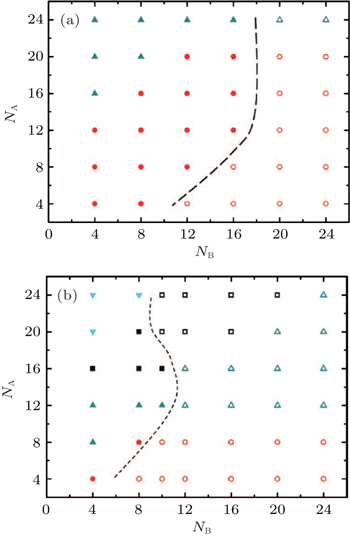 | Fig. 9. Phase diagram of symmetric ABA triblock copolymer brushes in a solvent that is selective to the B blocks with (a) σ = 0.0625 and (b) σ = 0.111 in the N A and N B space, where closed symbols represent micelles with only one A-rich layer, and open symbols represent micelles with two A-rich layers. The closed circles represent semispherical pinned micelles; the closed up-triangles, worm-like micelles; the closed squares, stripe structures; the closed down-triangles, perforated layer; the open circles, semi-spheres-spheres; the open up-triangles, worm-like micelles-spheres; the open squares, stripes-spheres. For micelles with two A-rich layers, they are named by a combination of the micelle names in the bottom A-rich layer and those in the top A-rich layer, separated by a “−” between them. The dashed line represents the phase boundary between structures with one and two A-rich layers. [ 84 ] Reprinted with permission from Xu J, Yin Y, Wang Z, Jiang R, Li B and Shi A C 2013 J. Chem. Phys. |
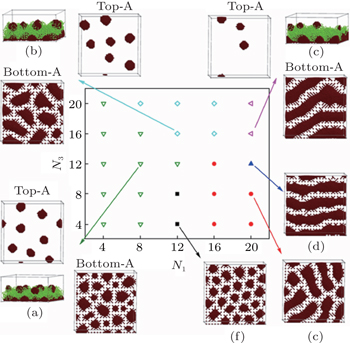 | Fig. 10. Phase diagram of ABA triblock copolymer brushes in a solvent that is selective to the B blocks for system with N 2 = 12 and σ = 0.111 in the N 1 and N 3 space. Closed symbols represent micelles with only one A-rich layer, and open symbols represent micelles with two A-rich layers. (f) The closed squares represent semispherical pinned micelles; (e) the closed circles, worm-like micelles; (d) the closed up-triangles, stripe structures; (a) the open down-triangles, semi-spheres-spheres; (b) the open diamonds, wormlike micelles-spheres; (c) the open left-triangles, stripes-spheres. The corresponding snapshots are also provided, where for micelles with one A-rich layer, only top views with A-monomers are shown. For micelles with two A-rich layers, the top views for both the top and bottom A-rich layers, and the side view with both A- and B-monomers are shown, and the micelles are named by a combination of the micelle names in the bottom A-rich layer and those in the top A-rich layer, separated by a “−” between them. [ 85 ] Reprinted from Ref. [ 85 ]. |
In this review, we have summarized the self-assembly behavior of three different cases of flat substrate-grafted block copolymers, and emphasized the theoretical and simulation results. The most important conclusion in all three cases is that the self-assembled morphologies can be tuned by changing many parameters. Hence, grafting block copolymer chains onto a substrate to form polymer brushes is a versatile method to fabricate surfaces with nanoscale patterns and environmentally responsive properties.
Although a great number of papers have been devoted to the study of grafted block copolymers, many questions still remain unanswered. One question is related to the distribution of grafting points. Usually, simulations are conducted assuming the grafting points are uniformly distributed. [ 53 , 67 , 79 , 84 , 85 ] This assumption is certainly an idealization. In experimental systems, it is likely that there are some fluctuations in the distribution of grafting points. It has been argued that the randomness of grafting points in distribution can result in lateral structures that lack long-range periodicity. [ 62 ] It is imperative to investigate further the global and local changes that occur to the brush structure and responsive properties due to the nonuniform distribution of grafting points.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 | |
| 67 | |
| 68 | |
| 69 | |
| 70 | |
| 71 | |
| 72 | |
| 73 | |
| 74 | |
| 75 | |
| 76 | |
| 77 | |
| 78 | |
| 79 | |
| 80 | |
| 81 | |
| 82 | |
| 83 | |
| 84 | |
| 85 | |
| 86 | |
| 87 | |
| 88 | |
| 89 | |
| 90 | |
| 91 |


