Project support by the NSF (Grant Nos. CMMI 1100205 and DMR 1410936).
Rechargeable batteries, such as lithium-ion batteries, play an important role in the emerging sustainable energy landscape. Mechanical degradation and resulting capacity fade in high-capacity electrode materials critically hinder their use in high-performance lithium-ion batteries. This paper presents an overview of recent advances in understanding the electrochemically-induced mechanical behavior of the electrode materials in lithium-ion batteries. Particular emphasis is placed on stress generation and facture in high-capacity anode materials such as silicon. Finally, we identify several important unresolved issues for future research.
Energy storage with high performance and low cost is critical for applications in consumer electronics, zero-emission electric vehicles, and stationary power management. [ 1 , 2 ] Lithium-ion batteries (LIBs) are the widely used energy storage systems due to their superior performance. [ 3 ] The operation of an LIB involves repeated insertion and extraction of Li ions in active battery electrodes, which are often accompanied with considerable volume changes and stress generation. [ 4 – 13 ] In the development of next-generation LIBs, mechanical degradation in highcapacity electrode materials arises as a bottleneck issue. The high-capacity electrode materials usually experience large volume changes (e.g., up to about 280% for Si), leading to high stresses and fracture in electrodes during electrochemical cycling. [ 14 – 23 ] Fracture causes the loss of active materials and yields more surface areas for solid electrolyte interphase (SEI) growth, both of which contribute to the fast capacity fade of LIBs. In addition, the mechanics issues are prominent at the battery pack and cell levels due to the requirements of structural integrity and crash safety for operating LIBs in hybrid and all electric vehicles. [ 24 ]
In this paper, we present an overview of recent advances in studying the mechanics of solid-state electrode materials in LIBs, with an emphasis on fundamentals of stress generation, stress-electrochemistry coupling, and fracture in high-capacity electrode materials such as Si. There are several recent review papers on the phenomenology and mechanisms of lithiation and delithiation in high-capacity electrodes. [ 20 , 25 , 26 ] Here we present selected examples to highlight the new understanding of coupled electro-chemo-mechanical phenomena as well as the new knowledge of mechanical properties of high-capacity electrodes.
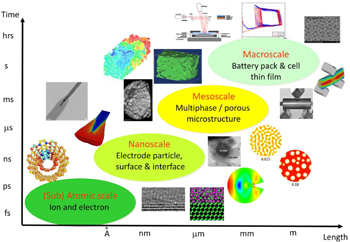
The mechanics of LIBs deals with inherently multiscale phenomena. Figure
The coupled electro-chemo-mechanical phenomena are extremely rich in LIBs. Below we begin with a review of the experimental and modeling studies of stress generation in thin films and particles. Then we proceed to review the recent progress in studying the effects of stress on lithiation kinetics and mechanical degradation in electrodes. These mechanistic studies advance our understanding of the electro-chemomechanical processes in LIBs, and they also highlight the critical need for a quantitative characterization of the mechanical properties of electrode materials, which is an important topic that will be reviewed in Section 4.
High-capacity electrode materials typically experience large volume changes during Li insertion and extraction. For the conversion-type anode material such as Si, its lithiation at room temperature usually yields amorphous Li 3.75 Si ( a - Li 3.75 Si), resulting in a volume increase of about 280%. Such a large volume expansion can be largely removed upon delithiation. Under constraints, the large volume changes lead to stress generation in the electrode materials. The resulting stresses can be very high, causing plastic flow. Sethuraman et al. [ 9 ] have used in situ wafer-curvature techniques to measure the stress evolution in thin films of a -Si during Li insertion and extraction. Figure
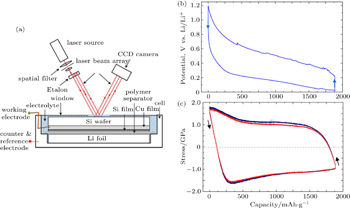 | Fig. 2. In situ measurement of stress evolution in an a -Si thin film during lithiation. [ 9 ] (a) Schematic of the in situ curvature technique for measuring stresses in lithiated thin film. (b) Cell potential versus capacity curve corresponding to lithiation and delithiation of a -Si thin-film electrode cycled at a rate of C/4. (c) Corresponding biaxial stress measured in the film. |
Stress generation in particles and wires with curved geometries, which are the common building blocks of electrodes, is different from that in flat thin films. This is because the curvature effect can be significant during stress generation in spherical particles and cylindrical wires, particularly when a two-phase mechanism is involved. In situ TEM experiments have shown that the lithiation of Si particles, with either a starting crystalline [ 17 ] or amorphous [ 19 ] phase, usually proceeds through the formation of a core-shell structure, involving the movement of a two-phase boundary that separates the inner core of pure Si with the outer shell of a -Li x Si ( x ∼ 3.75). Such a sharp phase boundary suggests that the Li-poor and Li-rich phases do not transform continuously into each other with changing composition. That is, there is a large solubility gap (i.e., Δ x ) between the two phases, manifested as an abrupt change of Li concentrations across the phase boundary.
Huang et al . have developed a chemo-mechanical model to analyze the stress evolution during two-phase lithiation of a spherical Si particle (Fig.
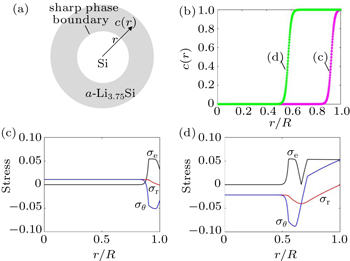 | Fig. 3. Modeling of stress generation in a spherical Si particle undergoing two-phase lithiation. [ 30 ] (a) Schematic of the two-phase model with a sharp phase boundary between the Si core and a -Li 3.75 Si shell. (b) Numerical results showing the radial distribution of Li concentration c normalized by its maximum value at the fully lithiated state, and the radial distance r is normalized by the current radius R of a partially lithiated particle which increases as lithiation proceeds. (c), (d) Numerical results showing the radial distribution of the von Mises effective stress σ e , radial stress σ r , and hoop stress σ θ = σ φ (normalized by Young’s modulus). |
To provide a physical interpretation of the reversal of hoop compression to tension in the surface layer, figure
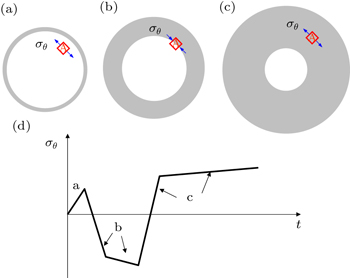 | Fig. 4. Illustration of the change of hoop stress σ θ with time t in a spherical particle, which contains a moving two-phase boundary between the pristine core (white) and lithiated shell (grey). [ 30 ] (a)–(c) σ θ in a representative material element A near the surface. As the phase boundary moves toward the center of the particle, progressive lithiation results in a gradual expansion of the particle, leading to the reversal of hoop compression in panel (b) to hoop tension in panel (c). (d) Schematic plot of σ θ versus t in element A. |
It is important to emphasize that the reversal of hoop compression to tension arises due to the curvature effect of the phase boundary; namely, behind the curved phase boundary, there are larger areas in the hoop direction at larger radial distances. Such reversal will not occur if the phase boundary is flat as in the case of two-phase lithiation in a thin film. More importantly, the high tensile stress and associated tensile plastic flow in the surface layer can cause fracture of electrode particles during Li insertion, which will be discussed in detail in Section 3.4. Finally, we note that for cylindrical wires, a similar conclusion can be drawn for the curvature effect on the reversal of hoop compression to tension in the surface layer of the wires.
The coupling between electrochemistry and mechanics is usually strong in high-capacity electrode materials. For example, high stresses can be induced during electrochemical lithiation of Si, as discussed in Sections 3.1 and 3.2. Such high stresses, in turn, can affect the rate of lithiation. Liu et al . conducted the in situ TEM study of lithiation kinetics in a c -Si nanowire. [ 31 ] Figures
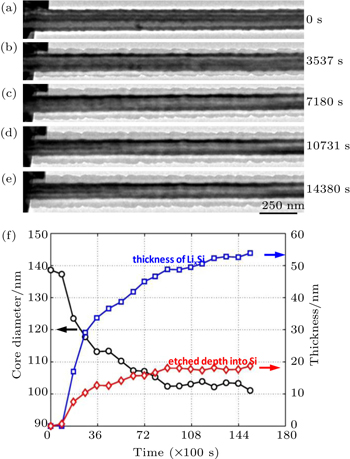 | Fig. 5. In situ TEM experiment of self-limiting lithiation in a Si nanowire. [ 31 ] (a)–(e) Time-lapsed images showing the evolution of the c -Si core and a -Li 3.75 Si shell in the nanowire in 4 hours. (f) Plots of nanowire diameter, etched depth, and thickness of the a -Li 3.75 Si shell versus time. |
The self-limiting lithiation can be reasonably attributed to the retardation effect of lithiation-induced stresses. As discussed in Section 3.2, large compressive stresses can build up in the lithiated shell, owing to the geometrical constraints from the unlithiated c -Si core. At this moment, there is a lack of experimentally measured chemo-mechanical properties of Li x Si such as chemical strains of Li insertion and elastoplastic properties of Li x Si, all of which can depend sensitively on Li concentration. As a result, the quantitative stress distribution in lithiated Si cannot be determined. Therefore, it remains an open question whether the self-limiting lithiation is dominantly controlled by the stress-retarded reaction at the two-phase boundary or the stress-retarded diffusion within the lithiated shell behind the two-phase boundary.
The electrochemically-induced stresses often cause the mechanical degradation in electrode materials. In situ TEM experiments by Liu et al. [ 17 ] have revealed a strong size dependence of fracture in Si nanoparticles, i.e., there exists a critical particle diameter D c of ∼ 150 nm, below which the particles neither cracked nor fractured upon first lithiation, and above which the particles initially formed surface cracks and then fractured due to lithiation-induced swelling.
Figure
 | Fig. 6. In situ TEM observation of cracking in a c -Si nanoparticle during lithiation. [ 17 ] (a) A c -Si nanoparticle with the initial diameter of 540 nm. (b) A core–shell structure forms as lithiation progresses, and the lithiation-induced swelling causes crack initiation at the particle surface. |
Surface cracking in large Si nanoparticles arises due to the buildup of a large hoop tension that reverses the initial compression in the surface layer, as discussed in Section 3.2. While the resulting hoop tension tended to initiate surface cracks, the small-sized nanoparticles nevertheless averted fracture. This is because the stored strain energy from electrochemical reactions is insufficient to drive crack propagation, as dictated by the interplay between the two length scales, i.e., particle diameter and crack size, that control the fracture. More specifically, the crack extension is controlled not only by the high stresses but also by the size of the highstress region that is dictated by the interplay between two length scales, i.e., particle diameter and flaw size. When a crack-like flaw of length a is formed in a large particle, near the crack faces the lithiation-induced tensile stress is relaxed to zero, and far from them it is unchanged. Approximately, a region of size a around the crack is relieved of its elastic energy, and this energy release is insensitive to the particle size. However, when the particle size is reduced to be comparable to the crack size, the region of zero stress near the crack faces and accordingly that of elastic energy relief become dependent on the particle size. The smaller the particle is, the less the stress-relief volume, and the lower the elastic energy release. A crack will not extend if the driving force of strain energy release rate is less than the resistance of surface energy. This explains the observation of the critical particle size in averting fracture during lithiation experiments.
 | Fig. 7. In situ TEM observation of lithiation of two small c -Si nanoparticles without fracture. [ 17 ] (a) Two pristine c -Si nanoparticles, marked by “A” and “B” with diameters of 80 and 40 nm, respectively. There is a twin boundary (TB) in the center of particle A. (b) A partially lithiated state with a core–shell, two-phase microstructure in the two nanoparticles. (c) Neither cracking nor fracture occur in the two Si nanoparticles after full lithiation, and but both nanoparticles have ∼ 280% volume expansion. |
In order to understand and mitigate the mechanical degradation in LIBs, it is essential to quantitatively characterize the fundamental mechanical properties of high-capacity electrode materials. Using Si as an example, here we review recent progress in the quantitative experimental characterization of mechanical properties of Li–Si alloys, which involve a large range of Li:Si ratio from 0 to 3.75.
Hertzberg et al. conducted the nanoindentation testing on polycrystalline Si thin films at various stages of lithiation. [ 34 ] They reported a strong dependence of Young’s modulus and hardness on the Li to Si ratio. Young’s modulus was found to decrease from an initial value of 92 GPa for pure Si to 12 GPa for Li 3.75 Si, and the hardness changes from 5 GPa to 1.5 GPa, correspondingly. Chon et al. used the curvature measurement technique to determine the yield stress in a lithiated Si thin film. [ 16 ] They reported a yield stress of 0.5 GPa for a -Li 3.5 Si, and other thin film lithiation experiments reported similar values. [ 35 ] Kushima et al. measured the fracture strength and plasticity of lithiated Si nanowires by in situ TEM tensile testing. [ 36 ] The tensile strength decreased from the initial value of about 3.6 GPa for pristine Si nanowires to 0.72 GPa for a -Li x Si ( x ∼ 3.5) nanowires. They also reported the large fracture strains that range from 8%–16% for a -Li x Si ( x ∼ 3.5) nanowires, 70% of which remained unrecoverable after fracture. Pharr et al. measured the fracture energy of lithiated Si thin-film electrodes as a function of Li concentration. The fracture energy was determined to be Γ = 8.5 ± 4.3 J/m 2 at small Li concentrations (∼ Li 0.7 Si) and has bounds of Γ = 5.4 ± 2.2 J/m 2 to Γ = 6.9 ± 1.9 J/m 2 at larger Li concentrations (∼ Li 2.8 Si). Recently, Wang et al. performed fracture toughness measurements by nanoindentation on lithiated a -Si thin films. [ 37 ] Their results showed a rapid brittle-to-ductile transition of fracture as the Li:Si ratio was increased to above 1.5. They reported the fracture energy of a -Si as 2.85 ± 0.15 J/m 2 and Li 1.09 Si as 8.54 ± 0.72 J/m 2 , respectively.
It is important to note that several recent experimental studies have measured the time-dependent mechanical properties of lithiated Si. Boles et al. conducted uniaxial tensile and creep testing of fully lithiated Si nanowires. [ 38 ] Their creep testing was performed at fixed force levels above and below the tensile strength of the material. A linear dependence of the strain rate on the applied stress was evident below the yield stress of the alloy, indicating viscous deformation behavior. Pharr et al. also studied the rate effect on stress generation in Si thin films. [ 39 ] They varied the rate of lithiation of a -Si thin films and simultaneously measured stresses. An increase in the rate of lithiation resulted in a corresponding increase in the flow stress. These observations indicate that rate-sensitive plasticity occurs in a -Li x Si electrodes at room temperature and at charging rates typically used in LIBs. Recently, Berla et al. studied the time-independent and time-dependent mechanical behavior of electrochemically lithiated Si with nanoindentation. [ 40 ] Their nanoindentation creep experiments demonstrated that lithiated Si creeps readily, with the observed viscoplastic flow governed by power law creep with large stress exponents (> 20). This research emphasizes the importance of incorporating viscoplasticity into lithiation/ delithiation models.
The mechanical properties of a -Li x Si alloys have also been studied using quantum mechanical and interatomic potential calculations. Shenoy et al. performed the density functional theory (DFT) calculations of the elastic properties of a -Li x Si alloys. [ 41 ] They showed the elastic softening with increasing Li concentration. Zhao et al. conducted DFT calculations for both the biaxial yield stress in a -Li x Si thin films and the uniaxial yield stress in bulk a -Li x Si under tension. [ 42 ] They found large differences between the characteristic yield stress levels of the two cases. Cui et al. developed a modified embedded atomic method (MEAM) interatomic potential for the Li x Si alloys. [ 43 ] They performed molecular dynamics simulations of uniaxial tension for bulk a -Li x Si at 300 K and showed that the yield strength decreased from about 2 GPa for a -LiSi to 0.5 GPa for a -Li 3.75 Si. Fan et al. performed molecular dynamics simulations to characterize the mechanical properties of a -Li x Si with a reactive force field (ReaxFF). [ 44 ] They computed the yield and fracture strengths of a -Li x Si alloys under a variety of chemo-mechanical loading conditions. The effects of loading sequence and stress state were investigated to correlate the mechanical responses with the dominant atomic bonding, featuring a transition from the covalent glass to the metallic glass characteristics with increasing Li concentration. In addition, quantum mechanical calculations have been performed to study the atomic structures and energetics associated with Li diffusion and reaction in a -Li x Si alloys. [ 45 – 53 ] The aforementioned modeling studies not only provide valuable insights into the mechanical properties of a -Li x Si, but also highlight the challenges to understand the structure-property relationship in a -Li x Si. Namely, the composition and structure can change drastically during electrochemical cycling of Si electrodes, involving for example the transition from a Lipoor network glass to a Li-rich metallic glass with increasing Li concentration during lithiation. [ 54 , 55 ]
In conclusion, the mechanics of LIBs is an emerging and exciting research field. Mitigation of mechanical degradation in high-capacity electrode materials is one of the principal challenges facing the development of next-generation high performance LIBs. Among a vast list of potentially intriguing directions for future research, several areas present particularly pressing needs.
Finally, we note that tackling the above mechanics problems presents many challenges and opportunities for experimentalists and modelers to work together. Hopefully, the synergistically integrated experiment and modeling will help understand, control, and optimize the mechanical behavior of electrodes, SEIs, and cell systems, thereby enabling the development of high-performance LIBs.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 |