† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61505236), the Innovation Program of Shanghai Institute of Technical Physics, China (Grant No. CX-2), and the Program of Shanghai Subject Chief Scientist, China (Grant No. 14XD1404000).
We present the numerical results for the optimization of the pump-to-idler conversion efficiencies of nanosecond idler wavelength tunable cascaded optical parametric oscillators (OPO) in different wavelength tuning ranges, where the primary signals from the OPO process are recycled to enhance the pump-to-idler conversion efficiencies via the simultaneous difference frequency generation (DFG) process by monolithic aperiodically poled, magnesium oxide doped lithium niobate (APMgLN) crystals. The APMgLN crystals are designed with different chirp parameters for the DFG process to broaden their thermal acceptance bandwidths to different extents. The idler wavelength tuning of the cascaded OPO is realized by changing the temperature of the designed APMgLN crystal and the cascaded oscillation is achieved in a single pump pass singly resonant linear cavity. The pump-to-idler conversion efficiencies with respect to the pump pulse duration and ratio of OPO coefficient to DFG coefficient are calculated by numerically solving the coupled wave equations. The optimal working conditions of the tunable cascaded OPOs pumped by pulses with energies of 350 μJ and 700 μJ are compared to obtain the general rules of optimization. It is concluded that the optimization becomes the interplay between the ratio of OPO coefficient to DFG coefficient and the pump pulse duration when the idler wavelength tuning range and the pump pulse energy are fixed. Besides, higher pump pulse energy is beneficial for reaching higher optimal pump-to-idler conversion efficiency as long as the APMgLN crystal is optimized according to this pump condition. To the best of our knowledge, this is the first numerical analysis of idler wavelength tunable cascaded OPOs based on chirp-assisted APMgLN crystals.
Highpower mid-infrared (MIR) laser sources are widely adopted in a variety of applications including environmental monitoring and MIR counter measurement. [ 1 , 2 ] As one of the most popular techniques for MIR generation, the quasi-phase-matched (QPM) optical parametric oscillator (OPO) has been extensively investigated in the past few years. [ 3 – 11 ] Despite the large effective nonlinear coefficient, excellent power handling capability and wide transparency range of QPM crystals, the pump-to-idler conversion efficiencies of typical nanosecond OPOs are around half of their quantum efficiencies owing to the inefficient parametric conversion in the build-up stage and the parametric back-conversion in the trailing edge of the pump pulses during oscillation. Although tailoring the pulse shapes and/or the spatial profiles of the pump lasers has shown the enhancement in pump-to-idler conversion efficiencies of such nanosecond OPOs, [ 11 – 13 ] the Manley–Rowe relations still constrain the conversion efficiency from further improvement.
In order to break this restriction, the concept of cascaded OPO was proposed to enhance the pump-to-idler conversion efficiency by converting part of the unwanted signal power produced from the former crystal into the idler output via the intra-cavity difference frequency generation (DFG) of a succeeding crystal. [ 14 ] Nonetheless, the insertion of the second crystal would inevitably increase the loss and detuning sensitivity of the OPO cavity. Monolithic dual grating periodically poled [ 15 ] and aperiodically poled ferroelectric crystals [ 16 – 19 ] were developed thereafter to reduce the unnecessary loss and to improve the long-term stability. However, the idler wavelengths of these cascaded OPOs were fixed because the pump-to-idler conversion efficiencies could be enhanced only if the primary OPO and secondary DFG processes are phase matched simultaneously. [ 18 , 19 ] By simply changing the pump wavelength and/or the crystal temperature, the idler wavelengths produced from the OPO and DFG processes will vary differently, which is predicted by the temperature-dependent Sellmeier equation. [ 20 ] The deviation of idler wavelengths will make the DFG process no longer phase matched and the primary signal produced from the OPO process cannot be converted into the idler output. As a result, the high intensity of the intra-cavity primary signal will lead to a dramatic decrease in pump-to-idler conversion efficiency due to the severe back-conversion effect during the OPO oscillation. [ 15 – 19 ] Although monolithic dual-grating crystals with a uniform grating section for the OPO process followed by a fan-out section for the DFG process could solve the crisis to some extent. [ 21 , 22 ] The idler wavelength tuning was realized by moving the crystal position together with precise temperature control, and tandem structure would make the cascaded parametric conversion unidirectional. As a better alternative, a specially designed aperiodically poled magnesium oxide doped lithium niobate (APMgLN) crystal with a chirp parameter for the DFG process was proposed to increase the thermal acceptance bandwidth. [ 23 ] Consequently, the idler wavelength could be tuned by the crystal temperature and the pump-to-idler conversion efficiency could be improved by the secondary DFG process within the thermal acceptance bandwidth. However, the relative strength of the two simultaneously phase matched processes and the idler wavelength tuning ranges were fixed in the previous experiment. Therefore, the performance of the cascaded OPO was not likely to be optimal under different pump energies and the fixed idler wavelength tuning range could hardly meet the requirements for different practical applications. Clearly, optimizing the APMgLN crystal design prior to the construction of a cascaded OPO instead of searching the optimal crystal structure during the experiment would reduce the material cost and time consumption to a great extent. Besides, employing the most suitable crystal designed for practical pump conditions would make the cascaded OPO easier to oscillate and to achieve the highest pump-to-idler conversion efficiency during the experiment.
In this paper, we report our recent investigations on the optimization of the idler wavelength tunable cascaded OPOs based on chirp-assisted APMgLN crystals. A chirp parameter is introduced into the DFG process in the design procedure of APMgLN crystal enabling the temperature tuning of the idler wavelength. The idler wavelength tuning range can vary by modifying the chirp parameter during crystal design. Besides, the relative strength of the Fourier coefficients for the OPO and DFG processes is also adjustable in order to maximize the pump-to-idler conversion efficiency. The pump-to-idler conversion efficiencies of such cascaded OPOs with different idler wavelength tuning ranges pumped by pulses with various durations are calculated by numerically solving the coupled wave equations. The optimal design of the crystal and the most suitable pump pulse duration regarding the highest pump-to-idler conversion efficiency are obtained for each idler wavelength tuning range from the numerical simulation. General rules of optimization for the pump-to-idler conversion efficiency of cascaded OPO are obtained by comparing the optimal working conditions employing pump pulses with energies of 350 μJ and those with energies of 700 μJ, respectively. To the best of our knowledge, this is the first ever-reported numerical analysis of idler wavelength tunable cascaded OPOs based on chirp-assisted APMgLN crystals. We believe that our investigations on the optimization of the idler wavelength tunable cascaded OPOs are of significance in constructing efficient practical cascaded OPOs in different desired idler wavelength tuning ranges.
In this section, the model of the cascaded OPO and the simulation method are described in detail. Firstly, the design procedure of the APMgLN crystals and the practical considerations are explained. Then a brief description of the schematic arrangement of the cascaded OPO is given. Finally, the coupled wave equations for numerical simulation are listed.
The APMgLN crystals employed in the cascaded OPO were designed to generate MIR emission in different wavelength tuning ranges. Therefore, an adjustable chirp parameter was introduced into the crystal modulation function to change the thermal acceptance bandwidths of the APMgLN crystals. Besides, another parameter changing the relative strength of the Fourier coefficients for the OPO and DFG processes was also taken into consideration for optimizing the pump-to-idler conversion efficiency. Thus, the design of the APMgLN crystal started from the following initial guess:
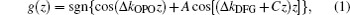
We assumed that the pump wavelength and the idler wavelength for the cascaded OPO were 1064 nm and ∼ 3.8 μm, respectively. Hence, the reciprocal vectors related to the OPO and DFG processes of the designed APMgLN crystal, Δ k OPO and Δ k DFG , were computed to be 0.213 μm −1 and 0.187 μm −1 , respectively, making the calculated idler wavelengths for OPO and DFG processes coincide at 3.83 μm at room temperature. The comparatively long idler wavelength at room temperature was selected on account of the fact that the idler wavelength would down-shift when the crystal temperature rose. The crystal length was assumed to be 50 mm and the step size of the Z parameter during design was set to be 0.2 μm, which was the same as the resolution of our phase mask lithography. During the preliminary design, there would appear some tiny domains with widths less than 5 μm, whose poling quality cannot be guaranteed using our self-developed high voltage triggering technique. These domains would then merge into the adjacent domains, leading to the slight change of the Fourier coefficients. Therefore, a normalized Fourier transform was carried out afterwards to verify the actual coefficients and the relevant adjustment was made on the A parameter thereafter to correct the deviation. This procedure would iterate several times until the final design was accomplished, in which the tuning bandwidth and the relative strength of Fourier coefficients were optimized as expected. The normalized Fourier transform of the grating modulation function g ( z ) could be calculated by
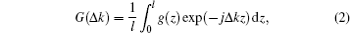
The schematic arrangement of the idler wavelength tunable cascaded OPO is depicted in Fig.
There are four major waves in the cavity of the cascaded OPO. At first, the pump wave generates the primary signal wave and the idler wave through the OPO process when the pump intensity just exceeds the oscillating threshold. As the intensity of the primary signal grows as the pump intensity increases, the primary signal starts to amplify the idler wave via the phase matched DFG process accompanied by the generation of the secondary signal wave. Owing to the collinear interaction scheme of the QPM-based nonlinear crystal, no walk-off effect should be considered in the nonlinear conversion. Employing the slowly varying envelope and paraxial approximation, the coupled wave equations for the four intra-cavity interacting waves can be derived as follows:
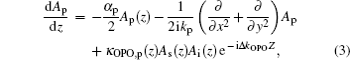
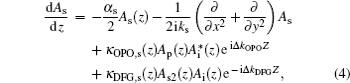
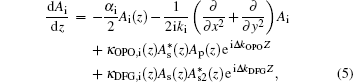
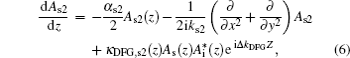
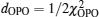
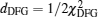
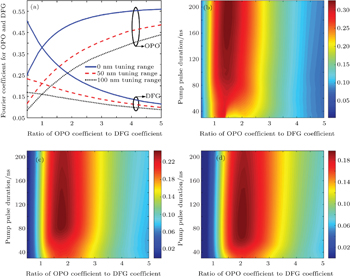
In order to verify the validity of the APMgLN design method with a linear chirp parameter for DFG process broadening the idler wavelength tuning range, the crystal temperature and idler wavelength tuning ranges each as a function of chirp parameter C in Eq. (
Once the idler wavelength tuning range is determined by selecting a proper value for the chirp parameter C , the performance of such cascaded OPO could be optimized afterwards by adjusting the other variable A in Eq. (
Apparently, both the ratio of OPO coefficient to DFG coefficient and the pump pulse duration have influences on the pump-to-idler conversion efficiency of a wavelength tunable cascaded OPO. In terms of the ratio of OPO coefficient to DFG coefficient, the highest pump-to-idler conversion efficiency appears when these ratios are larger than 1 in all the three cases with idler wavelength tuning in a range from 0 nm to 135 nm. It is clear that the OPO process takes place prior to the DFG process and dominates the threshold of the cascaded OPO. As long as the pump power of a cascaded OPO exceeds its threshold, the primary signal will grow dramatically due to the high reflectivities of the cavity mirrors in this band. Consequently, the highintensity intra-cavity primary signal wave will amplify the idler wave to a great extent via DFG process, and thus clamping its own intensity to a certain level. An appropriate ratio of OPO coefficient to DFG coefficient can not only reduce the threshold of a cascaded OPO but also effectively convert the intra-cavity primary signal into the idler wave, which are both favorable for efficient idler wave generation. When the idler wavelength tuning range extends from 0 nm to 135 nm, the optimal ratio of OPO coefficient to DFG coefficient rises slightly from 1.5 to 2 with the dramatic decline in the absolute value of the Fourier coefficient for the DFG process. Such a severer reduction is attributed to the priority of the OPO process dominating the threshold and the overall Fourier coefficient decrease resulting from the expansion of the idler wavelength tuning range. As a consequence, the maximum pump-to-idler conversion efficiency decreases from 32% to 19.5% as the idler wavelength tuning range is stretched from 0 nm to 135 nm. Besides, the pump pulse duration plays a minor role in the conversion efficiency of a cascaded OPO other than the ratio of OPO coefficient to DFG coefficient. Figures
Figure
Undoubtedly, pump pulses with higher energy are beneficial to obtaining higher optimal pump-to-idler conversion efficiencies from such wavelength tunable cascaded OPOs. Although the corresponding optimal pulse durations of the 700 μJ pump are about half of those of the 350 μJ pump, thus leading to comparable peak power in the two cases, the pump-to-idler conversion efficiencies of OPO pumped by 700 μJ pulse energy are still higher, especially for wider idler wavelength tuning ranges. This is attributed to the smaller rate of build-up time to pump pulse duration for pump pulses with longer durations, even if the APMgLN crystals are designed with slightly different ratios of OPO to DFG coefficient. Clearly, the smaller rate of build-up time to pump pulse duration is advantageous because the back-conversion effect of such a cascaded OPO is significantly relieved and efficient pump-to-idler conversion will take place from the build-up to the trailing edge of the pump pulses. Therefore, this value almost represents the conversion efficiency of a typical nanosecond cascaded OPO. As for the optimal ratio of OPO coefficient to DFG coefficient, different values should be selected in order to sustain high pump-to-idler conversion efficiencies for both pulse energies. The numerical results show that a large value is favorable for a wide idler wavelength tuning range and an even larger value should be adopted for pump pulses with lower energies. The reason is that the effective nonlinear coefficient for the OPO process should be guaranteed in preference to that of the DFG process for a wavelength tunable cascaded OPO. Besides, the overall Fourier coefficient for the OPO and DFG processes suffers severer reduction when the idler wavelength tuning range goes up. Hence, the ratio of OPO coefficient to DFG coefficient should be raised to maintain the absolute value of the Fourier coefficient for the OPO process so as to keep the ratio of build-up time to pump pulse duration at a certain level. It is believed that pump pulses with peak power of several kilo-Watt are already high enough to obtain a short build-up time when the idler waves are barely tunable because the absolute values of the Fourier coefficients for the OPO process are large, which could also be deduced in our previous report. [ 19 ] When the tuning bandwidth of the cascaded OPO is enlarged, pump pulses with shorter durations and APMgLN crystals with larger ratio of OPO coefficient to DFG coefficient should be employed to hold the rate of build-up time to pump pulse duration at the expense of lower DFG coefficients, leading to the inevitable reduction in overall pump-to-idler conversion efficiencies.
It is worth mentioning that the calculated pump-to-idler conversion efficiencies exceed the quantum limit, which is 28% for conventional single stage OPOs generating 3.8 μm from 1.064 μm, when the idler tuning ranges are less than 20 nm and 85 nm for pump pulses with energies of 350 μJ and 700 μJ, respectively. Though the tuning ranges might not be large enough for special applications such as broadband absorption spectroscopy, they are still among the most promising candidates in practical systems with the asset of both high efficiency and simple temperature management of the nonlinear crystals. Moreover, the numerical results reveal that the performance of such a tunable cascaded OPO is a compromise between the pump-to-idler conversion efficiency and the idler wavelength tuning range. For cascaded OPOs with large tuning ranges, pump pulses with low energies might not be suitable since the reflectivities for the primary signal band of the cavity mirrors can hardly be further improved to compensate for the delay of the build-up time. Therefore, the overall pump-to-idler conversion efficiencies are not likely to remain high when the pump pulse energy is rather low. In addition, when the idler wavelength tuning range and pump pulse energy are determined, the optimization for the conversion efficiency becomes the interplay between the ratio of OPO coefficient to DFG coefficient for the APMgLN crystal and the optimal duration for the pump pulses, though the ratio of OPO coefficient to DFG coefficient is crucial while the pump pulse duration only plays a minor role.
In this work, we numerically investigate the performance and general optimization rules of idler wavelength tunable cascaded OPO based on chirp-assisted APMgLN crystal. Proper chirp parameters for the DFG process are introduced into the design procedure of the APMgLN crystal, enabling the thermal wavelength tuning of the cascaded OPO with different bandwidths. By numerically computing the coupled wave equations, the pump-to-idler conversion efficiencies of such cascaded OPOs are calculated under different pump conditions, while utilizing various crystal designs. By comparing the numerical results, it is concluded that the rate of build-up time to the pump pulse duration, dominated by the ratio of OPO coefficient to DFG coefficient, is a crucial parameter in optimizing the pump-to-idler conversion efficiency of such cascaded OPO. Because the back-conversion effect is significantly relieved due to the secondary DFG process, conversion enhancement could always take effect after the build-up of the cascaded OPO. Pump pulses with higher energies are favorable to enhancing the pump-to-idler conversion efficiency of the cascaded OPO, especially for those with large idler wavelength tuning ranges. To the best of our knowledge, this is the first numerical analysis of the idler wavelength tunable cascaded OPOs based on chirp-assisted APMgLN crystal and we believe that our investigation is of great value for constructing practical cascaded OPOs with different desired idler wavelength tuning ranges.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 |