Cite this Article
Sun S Y, Miao X Y, Jia Xiang-Fu. Triple differential cross sections of magnesium in doubly symmetric geometry. Chinese Physics B , 2016, 25(1): 013401  
Permissions
Triple differential cross sections of magnesium in doubly symmetric geometry
Sun S Y , Miao X Y , Jia Xiang-Fu †,
School of Physics and Information Engineering, Shanxi Normal University, Linfen 041004, China

 

† Corresponding author. E-mail: jiaxf@sxnu.dns.edu.cn

Project supported by the National Natural Science Foundation of China (Grant No. 11274215).

Abstract
Abstract

A dynamically screened three-Coulomb-wave (DS3C) method is applied to study the single ionization of magnesium by electron impact. Triple differential cross sections (TDCS) are calculated in doubly symmetric geometry at incident energies of 13.65, 17.65, 22.65, 27.65, 37.65, 47.65, 57.65, and 67.65 eV. Comparisons are made with experimental data and theoretical predictions from a three-Coulomb-wave function (3C) approach and distorted-wave Born approximation (DWBA). The overall agreement between the predictions of the DS3C model and the DWBA approach with the experimental data is satisfactory.

PACS : 34.80.Dp ; 34.50.Fa
Keyword : dynamical screening ; single ionization ; triple differential cross section
1. Introduction

The (e, 2e) technique has been applied to a wide range of targets and kinematical arrangements since the first experimental studies of this type by Ehrhardt et al. [ 1 ] and Amaldi et al. [ 2 ] The different geometrical conditions available in the processes offer access to different types of information. [ 3 – 6 ] Theoretical investigations of (e, 2e) processes on atoms provide a platform to understand the collision dynamics and the characteristics of the targets by studying triple differential cross sections (TDCS). The experiments in the coplanar geometry on alkaline earth metal and alkali metal targets of Murray [ 7 ] have evoked a fresh interest in this problem.

On the theoretical side, a great deal of calculations have been carried out [ 8 – 14 ] for this particular process. For example, the nonperturbative convergent close-coupling (CCC) method, [ 15 , 16 ] which produces reliable results, has been successfully extended to calculate the triply differential cross sections for electron, sodium ionization by Bray et al. [ 8 ] and the perturbative distorted wave Born approximation (DWBA) have also been used to study the problem of electron, complex targets ionization by Srivastava et al. , [ 9 ] Hitawala et al. , [ 10 ] Khajuria et al. , [ 11 ] and Zhou et al . [ 12 – 14 ] Although their results qualitatively reproduced many features of the cross section and are in agreement with the experimental results of Murray, [ 7 ] significant discrepancies can still be noticed.

The three-Coulomb-wave (3C) [ 17 ] and the dynamically screened 3C (DS3C) [ 18 ] are well known and have been shown to be capable of predicting the shapes of cross sections for various types of (e, 2e) and positron-impact ionization processes. [ 17 – 19 ] The description was extended to (e, 2e) cross sections of sodium [ 20 , 21 ] and potassium [ 22 ] and reproduced most of the features of the triple differential cross section in agreement with the experimental results.

Following the idea of Ref. [ 20 ], we study the triple differential cross section of magnesium in the coplanar symmetric geometry using a parameterized optimized effective potential for the alkaline core, both in the determination of the bound state wave function of the target and in the interaction potential of the incoming electron with the target. The effect of dynamical screening has been studied. It is observed that the overall agreement between the predictions of the DS3C model with the experimental data is satisfactory.

2. Theoretical treatments

The (e, 2e) reaction can be represented as

Here, A is a target atom, A + is the ion left in the final state, e – are the incident and the two outgoing electrons respectively, E i , E 1 , E 2 and k i , k 1 , k 2 are energies and momenta of incident, scattered, and ejected electrons, respectively. The TDCS for the (e, 2e) process on a target as defined in Eq. ( 1 ) may be written as

where dΩ 1 and dΩ 2 denote, respectively, the elements of solid angles for the scattered and the ejected electrons, and d E 2 represents the energy interval of the ejected electron. The transition matrix elements T fi are given by

Here, and represent the wave functions describing the whole system in its final and initial states, respectively. The r 1 designates the position of the incident electron, r 2 the bound one, and V i represents the interaction between the incident electron and the target

with r 12 = | r 1 − r 2 |, and V 2 is the numerical-parameterized optimized effective potential (NPOEP), [ 23 , 24 ] which describes the interaction of the incident electron with the electrons of the alkaline core given by

Here Z is the nuclear charge of the target ion, and n i are positive integers and at least one of them is equal to zero. The coefficients c i and exponents b i are taken as variational parameters. The initial state , which takes into account the incident and the bound electrons, will be written as the product of a plane wave and the wave function of the valence electron of the alkaline atom

The ground-state wave function ϕ i ( r 2 ) is obtained by an expansion on the Slater basis

Here a i and α i are determined variationally and the normalization constant N i [ 23 ] is

The parameters a i , b i , c i , α i , and n i can be found in Ref. [ 23 ].

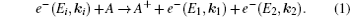
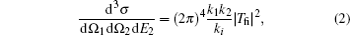
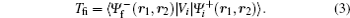
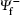
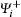
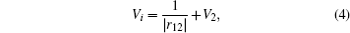
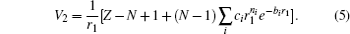
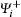
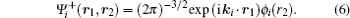
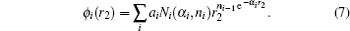
The final state is reduced to a three-body system by assuming that the residual ion (Mg + ) acts as a point charge on the two escaping electrons. It is approximated by a product of three two-Coulomb waves with dynamical coupling between the individual two-body subsystems (DS3C) being included

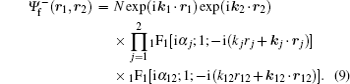
Here α j are Sommerfeld parameters, k 12 = ( k 1 – k 2 )/2, 1 F 1 is the confluent hypergeometric function, and N is a normalization factor.

Since the strength of the interaction of any two particles in the three-body Coulomb system is affected by the presence of the third one and the modification of the strength of a particular two-body Coulomb interaction depends on the momenta of the two particles relative to the third one, which represents a dynamic screening (DS) of the three two-body Coulomb interactions. Berakdar et al. [ 18 ] suggested the dynamic screening model to modify the 3C wave function by formulating effective charges. The modified Sommerfeld parameters are given by Ref. [ 18 ].

In the second calculation, we remove the dynamical screening in the final continuum state of the two electrons and the ion. This is carried out by replacing the dynamical Sommerfeld parameters in Ref. [ 18 ] by the standard Sommerfeld parameters, in which the final two-electron continuum state is represented by the 3C. [ 17 ]

3. Results and discussion

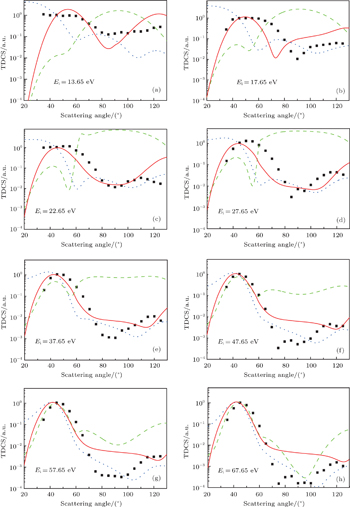The coplanar symmetric geometry triple-differential cross section for Mg at the incident energies of 13.65, 17.65, 22.65, 27.65, 37.65,47.65, 57.65, and 67.65 eV are presented in Figs.  1(a) – 1(h) , respectively, along with the recent experimental data of Murray [ 7 ] and the theoretical results of Hitawala et al. [ 10 ] performed in the DWBA with polarization for comparison. The results are presented on a logarithmic scale because of large variations in the cross section. All the results are normalized to unity at θ = 50°.

Fig. 1. Triple differential cross section (TDCS) for electron impact ionization of magnesium at incident energies of (a) 13.65 eV, (b) 17.65 eV, (c) 22.65 eV, (d) 27.65 eV, (e) 37.65 eV, (f) 47.65 eV, (g) 57.65 eV, and (h) 67.65 eV in the doubly symmetric geometries. The solid curve represents our DS3C calculations, the dashed curve corresponds to 3C results, and the dotted curve corresponds to DWBA results of Hitawala et al. , [ 10 ] whereas the solid circles are the experimental data from Murray. [ 7 ] Kinematics is displayed in each frame and the theoretical results and experimental data have been normalized to unity at the symmetric scattering angle θ = 50° for all the incident electron energies.

It can be seen from Fig.  1 that the cross sections show well-known binary and recoil lobe structure and the ratio of the forward to the backward scattering peaks is found to decrease with the increase of the excess energy of the incident electrons. The qualitative feature of the experimental TDCS is well theoretically predicted except for the 3C model, though some quantitative discrepancies remain.

It can be seen from Figs.  1(a) – 1(d) that the DWBA model did not yield substantial and consistent improvement in the agreement between experiment and theory. The peak position shifted toward smaller ejection angles in the DWBA angular distribution and the DWBA results yield unphysical values when the electrons both go in the forward angles. In the present geometry, the cross section for zero degree scattering should be zero since two equal energy electrons would not both come out in the forward direction. Very recently, Zhou’s group [ 14 ] has carried out second-order DWBA calculations and found that the second-order term is capable of effectively improving the description of the collision process for magnesium in the low energy range. With the increase in impact energy, the DWBA results agree better with the shape of the experimental data, especially for higher angle regions in the back-scattering region because of full consideration of the interaction between incident electron and atomic target.

In low incident energies (Figs.  1(a) – 1(d) ), there is a major deviation between the 3C theoretical results and experimental data. The 3C model clearly fails by lower forward peak and higher cross sections in the angular region of θ > 70°.

In addition, the trend is exactly opposite. With the increase in impact energy (Figs.  1(g) – 1(h) ), the agreement between 3C theory and the experiment gets better and the 3C calculations are gradually close to the experiment. As shown by Jones and Madison, [ 6 ] the 3C model, which has been fairly successful for higher energy collisions, fails to reproduce the angular distribution of the experimental data and does not work very well at the low energies.

Our results of the DS3C model approach nicely reproduce the general features, such as a broader forward peak and the decrease of the backward peak with respect to the 3C results. For the lower energies (Figs.  1(a) – 1(f) ), it is very encouraging to see that the DS3C calculations improve the degree of agreement with the experimental measurements. The DS3C calculations qualitatively reproduce the angular distribution and are in better agreement with the experiment in the forward peak and relative heights of the two peaks. Strong differences between DS3C and 3C resulting from dynamical screening can be observed. Comparison between the 3C and DS3C calculations shows that the DS3C model is capable of producing peak structures at low energies. At higher energies (Figs.  1(g) – 1(h) ), the qualitative feature of the experimental TDCS is quite well described by the 3C and DWBA calculations, but the DS3C calculations become relatively flat at higher angles and less satisfactory. This indicates that the DS3C wave function does not accurately represent the final-state wave function for a continuum electron in the field of an ion, here the passive electrons might have an important impact on the ionization results. [ 8 ] The projectile target interactions are more complicated for the two-valence-electron target Mg and using a one-electron model to describe the collision process of multielectronic targets is too simple.

4. Conclusion

As discussed above, the inclusion of the dynamical screening effects in the DS3C model improves the the degree of agreement between theoretical calculations and experimental measurements of coplanar symmetric (e, 2e) collisions for Mg, especially for the lower energies (Figs.  1(a) – 1(f) ). Unfortunately, some currently unresolved discrepancies still exist, which may be due to some missing corrections, such as interaction between incident electron and complex atomic target, screening of the nucleus provided by the passive electrons or polarization effects of atomic core, etc. Further theoretical studies will be preformed with the proper treatment of these corrections.

Reference
1 Ehrhardt H Schulz M Tekaat T Willmann K 1969 Phys. Rev. Lett. 22 89
2 Amaldi U Jr Egidi A Marconero R Pizzella G 1969 Rev. Sci. In-strum. 40 1001
3 Weigold E McCarthy I E 1978 Adv. At. Mol. Phys. 14 127
4 McCarthy I E Weigold E 1988 Rep. Prog. Phys. 51 299
5 Lahmam-Bennani A 1991 J. Phys. B 24 2401
6 Jones S Madison D H 2000 Phys. Rev. A 62 042701
7 Murray A J 2005 Phys. Rev. A 72 062711
8 Bray I Fursa D V Stelbovics A T 2008 J. Phys. B 41 215203
9 Srivastava M K Chauhan R K Srivastava R 2006 Phys. Rev. A 74 064701
10 Hitawala U Purohit G Sud K K 2008 J. Phys. B 41 035205
11 Khajuria Y Sunil Kumar S Deshmukh P C 2007 Phys. Rev. A 75 022708
12 Wang Y Jiao L G Zhou Y J 2012 Phys. Lett. A 376 2122
13 Wang Y Zhou Y J Jiao L G 2012 Chin. Phys. B 21 083401
14 Zhang Y Z Wang Y Zhou Y J 2014 Chin. Phys. B 23 063402
15 Bray I 1994 Phys. Rev. Lett. 73 1088
16 Bray I 2002 Phys. Rev. Lett. 89 273201
17 Brauner M Briggs J S Klar H 1989 J. Phys. B 22 2265
18 Berakdar J Briggs J S 1994 Phys. Rev. Lett. 72 3799
19 Jones S Madison D H 2002 Phys. Rev. A 65 052727
20 Jia X F Sun S Y 2011 Phys. Rev. A 83 032715
21 Sun S Y Jia X F Miao X Y Li X Ma X Y 2012 Acta Phys. Sin. 61 093402 (in Chinese)
22 Sun S Y Jia X F Miao X Y Zhang J F 2014 Phys. Rev. A 105 53002
23 Sarsa A Gálvez F J Buendía E 2004 At. Data Nucl. Data Tables 88 163
24 Buendia E Gálvez F J Maldonado P Sarsa A 2006 J. Phys. B 39 3575