Cite this Article
Wang Qing-Hui, Shao Xu-Ping, Yang Xiao-Hua. Stark effect of the hyperfine structure of ICl in its rovibronic ground state: Towards further molecular cooling. Chinese Physics B , 2016, 25(1): 013301  
Permissions
Stark effect of the hyperfine structure of ICl in its rovibronic ground state: Towards further molecular cooling
Wang Qing-Hui 1 , Shao Xu-Ping 1 , Yang Xiao-Hua 1, 2, †,
School of Science, Nantong University, Nantong 226019, China
State Key Laboratory of Precision Spectroscopy, East China Normal University, Shanghai 200062, China

 

† Corresponding author. E-mail: xhyang@ntu.edu.cn ; xhyang@phy.ecnu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant No. 11034002), the National Basic Research Program of China (Grant No. 2011CB921602), and Qing Lan Project, China.

Abstract
Abstract

Hyperfine structures of ICl in its vibronic ground state due to the nuclear spin and electric quadruple interactions are determined by diagonalizing the effective Hamiltonian matrix. Furthermore, the Stark sub-levels are precisely determined as well. The results are helpful for electro-static manipulation (trapping or further cooling) of cold ICl molecules. For example, an electric field of 1000 V/cm can trap ICl molecules less than 637 μK in the lowest hyperfine level.

PACS : 33.15.Pw ; 32.60.+i
Keyword : hyperfine structure ; Stark effect
1. Introduction

We know less about the hyperfine structures of molecules than the rotational structures, because the hyperfine structures are much more complicated and thus hard to model in theory, and they are also hard to observe in experiment due to Doppler broadening. However, thanks to the developments of molecular cooling (see, for example, Stark deceleration of chemically stable molecules, [ 1 – 3 ] diatomic alkali ultracold molecules from laser-cooled atoms, [ 4 – 7 ] and direct laser cooling of molecules [ 8 ] for details), single mode laser technique, and optical comb technique, the molecular hyperfine structures can be investigated precisely at present. Therefore, the experimental data can verify and improve the theory, which makes it possible to precisely study the weak interactions of the nuclear spin and the nuclear electric quadruple moment with electrons surrounding. In addition, the external field effects of the molecular hyperfine structures can be observed and modeled as well. Unique and complex molecular hyperfine structures together with their external field effects provide many opportunities for sensitive probing of fundamental physics and for related applications. External fields have been utilized to manipulate molecules at hyperfine level [ 4 ] and can be used for further cooling cold molecules at about 10 mK to ultracold molecules below 1 μK. [ 9 ]

The electronic ground state of the iodine chloride (ICl) molecule is of 1 Σ symmetry, so its rotational structures have neither Zeeman effect nor Stark effect. Its rotationally resolved spectra can be used as frequency standards for optical frequency calibration in the near infrared region instead of the iodine spectra. The spins of 35,37 Cl atoms are both 3/2 and the spin of 127 I atom is 5/2, and both atoms of ICl have relatively large electric quadruple moments, which result in complicated hyperfine structures. Therefore, ICl is a good candidate to fully understand the hyperfine interactions. Additionally, our recent study suggests that ICl can also be Stark decelerated assisted by a laser beam to the temperature of about 20 mK, which makes it possible to experimentally study the hyperfine structures together with their external field effects. The ICl molecule is the first diatomic molecule whose pure rotational spectrum is investigated by microwave spectroscopy, and its molecular constants B e and α e have been accurately determined. [ 10 , 11 ] Townes et al. obtained the nuclear electric quadruple moments, eQq 1 and eQq 2 , of the two atoms of I 35 Cl by analyzing the microwave spectra. [ 12 ] Thereafter, Slotterback et al. fully analyzed the hyperfine spectrum of I 35 Cl, [ 13 ] and Durand et al. determined the electric dipole moment ( μ ) of ICl. [ 14 ]

The hyperfine structures and their Stark effects of ICl in the rovibronic ground state are studied theoretically by diagonalizing the Hamiltonian matrix in the present work. Our results show that an electrostatic field can be employed for trapping and further cooling of cold ICl molecules.

2. Theory

The Hamiltonian of a molecule in an electric field consists of five parts: electron, vibration, rotation, hyperfine, and Stark parts. When studying the structure of a rovibronic state, the first two parts are constant and thus can be omitted in the Hamiltonian, and then the Hamiltonian can be written as [ 15 , 16 ]

where

Equation ( 2 ) represents the rotational Hamiltonian, where B v and D v are the rotational constant and its centrifugal distortion, [ 17 ] and J is the molecular total momentum excluding nuclear spins. Equation ( 3 ) represents the hyperfine Hamiltonian consisting of nuclear electric quadrupole–electronic electric field gradient interaction and nuclear spin-electronic orbital interaction, where e is the charge of an electron, T (2) ( Q ) and T (2) ( ∇ E ) are the second-order tensors of nuclear electric quadrupole and electronic electric field, respectively, I 1 and I 2 are the spins of I and Cl atoms, respectively, and C 1 and C 2 are the nuclear spin–electronic rotation interaction constants of I and Cl atoms, [ 18 , 19 ] respectively. Equation ( 4 ) represents the Stark Hamiltonian, where T (1) ( μ ) and T (1) ( E ) are the first-order tensors of molecular electric dipole and applied electric field, respectively.

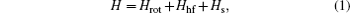
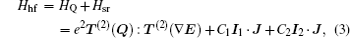
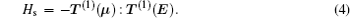
In the weak field limit, J , I 1 , F 1 , I 2 , F , and M F are good quantum numbers to describe the energy levels, and the coupling sequences are F 1 = I 1 + J and F = F 1 + I 2 . Therefore, the Hamiltonian matrices can be described in the | J I 1 F 1 I 2 FM F 〉 basis as [ 20 – 22 ]

with the selection rule of J ′ = J , J ± 2;

with the selection rules of J ′ = J , J ± 2 and F 1 ± 1, F 1 ± 2; and

where symbol { } is 6- j symbol and ( ) is 3- j symbol.

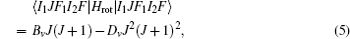
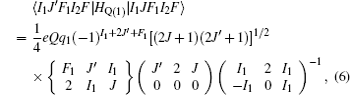
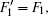
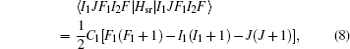
The Stark part of the Hamiltonian matrix is [ 22 ]

with the selection rules of J ′ = J ± 1, F 1 ± 1, and F ′ = F , F ± 1.

3. Results and discussion
3.1. Hyperfine structures

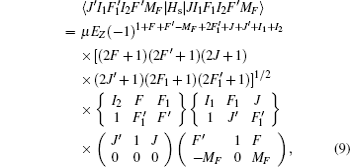
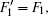
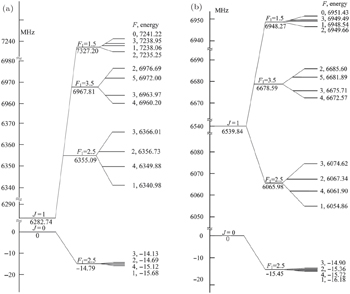
The hyperfine structures of the vibronic ground state of ICl are studied in this section. The spin of 127 I atom is 5/2, and the spins of 35,37 Cl atoms are both 3/2. As described in Section 2, we diagonalize the Hamiltonian matrix on the basis of | JI 1 F 1 I 2 F 〉 to obtain the hyperfine levels of J = 0 and 1 rotational states. The molecular constants adopted in the present calculation are listed in Table 1 . Note that, C 1 is small, which contributes a little to the hyperfine structure, and C 2 is so small that it is set to be 0 in our calculation. The results are plotted in Fig.  1(a) for I 35 Cl and Fig.  1(b) for I 37 Cl, and the quantum numbers and the corresponding level energies (in MHz) are labeled as well. The hyperfine structural differences of these two isotopologues arise from their different nuclear electric quadruples and rotational constants. As shown in Fig.  1 , the hyperfine structures only differ a little in value, while the level sequences are the same, so we only present the results of the richer I 35 Cl isotopologue subsequently. To give a distinct picture of how they come, the levels are plotted in three columns in Fig.  1 : the first column represents the rotational levels, the second represents the hyperfine levels only considering the contribution of I atom, and the third represents the real hyperfine levels (also considering the contribution of Cl atom). Here the assignments of the hyperfine energy levels are based on their eigenvectors. To verify our method, we calculate the hyperfine levels to compare with the experiments. [ 23 ] We find that all the calculations are in good agreement with the experiments within 0.07 MHz and the overall standard error is only 0.027 MHz.

Table 1.

Molecular constant (in MHz) of the v = 0 level in the X 1 Σ state of I 37,35 Cl.

.
Fig. 1. Hyperfine structures of J = 0 and 1 in the vibronic ground state of I 35 Cl (a) and I 37 Cl (b); the quantum numbers and the corresponding level energies are labeled as well.
3.2. Stark effects of the hyperfine structures

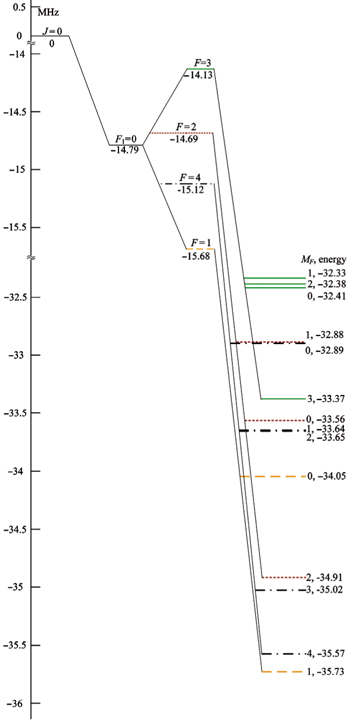When the Stark interaction of Eq. ( 9 ) is included, the Stark sub-levels can be computed by diagonalizing the Hamiltonian matrix. Figure  2 illustrates the Stark splitting of the rovibronic ground state of I 35 Cl at an applied electric field of 1000 V/cm. The Stark effect arises from the interaction of the nuclear electric quadruple with the external field. The Stark sub-levels are labeled with quantum number M F , where M F = 0, 1, …, F . The Stark sub-levels with different F are mixed, and thus, we use two ways to assign the sub-levels: one is assigning according to their eigenvectors, and the other is studying their Stark shifts varying with the applied electric field approaching to zero.

Fig. 2. Stark splitting of the | J = 0, F 1 = 0, F 〉 hyperfine levels in the vibronic ground state of I 35 Cl at an applied electric field of 1000 V/cm.

Figure  3 plots the Stark splitting of | J = 1, F 1 = 3.5, F = 4〉 state varying with the applied electric field up to 1000 V/cm. It shows that the Stark shift of the sub-levels can be either positive or negative. Thus, ICl can electrostatically be trapped both in their strong-field-seeking state and in their weak-field-seeking state at hyperfine level. For example, when ICl is at | J = 0, F 1 = 0, F = 1, M F = 1〉 (the lowest hyperfine) state, it can be trapped in the strong field region and the trap depth can be as high as 637 μK at the field of 1000 V/cm. Therefore, it is possible to construct an electric-optical trap (EOT) for cold ICl three-dimensional (3D) trapping in its lowest hyperfine level, which is illustrated in Fig.  4 . Note that, the laser frequency is red-detuning to the resonance of the trapped molecular transition.

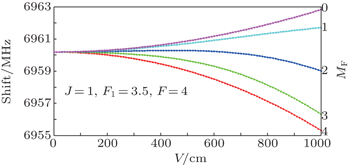Fig. 3. Stark shifts of the | J = 1, F 1 = 3.5, F = 4〉 hyperfine level in the vibronic ground state of I 35 Cl varying with the applied electric field.
Fig. 4. Schematic of an electric-optical trap for cold molecular trapping in its strong-field-seeking state, where the laser frequency is red-detuning to the resonance of the trapped molecular transition.

Recently, we proposed a laser-assisted Stark deceleration of ICl scheme, and it would most probably decelerate ICl to the equivalent temperature of about 20 mK. Therefore, if we trap and further cool the decelerated ICl via evaporation cooling method [ 9 ] with this EOT, ultracold ICl molecules below 10 μK with large volume would be obtained.

4. Conclusion

The hyperfine levels of the J = 0 and 1 levels of the vibronic ground state of I 35,37 Cl are precisely determined by diagonalizing the effective Hamiltonian matrix at the basis of | JI 1 F 1 I 2 F 〉, where the interactions due to nuclear magnetic dipole and nuclear electric quadruple are both taken into account. Subsequently, the Stark sub-levels due to the interaction of the nuclear electric quadruple with the external field are studied by employing the Hamiltonian matrix at the basis of | JI 1 F 1 I 2 FM F 〉 both at the fixed applied electric field of 1000 V/cm and at the applied field varying from 0 to 1000 V/cm. The results would be useful for electrical manipulation (trapping and further cooling) of ICl molecules at hyperfine level.

Reference
1 Bethlem H L Berden G Meijer G 1999 Phys. Rev. Lett. 83 1558
2 Bochinski J R Hudson E R Lewandowski H J Meijer G Ye J 2003 Phys. Rev. Lett. 91 243001
3 Hou S Y Li S Q Deng L Z Yin J P 2013 J. Phys. B 46 045301
4 Ospelkaus S Ni K K Quémener G de Miranda M H G Neyenhuis B Wang D Bohn J L Ye J Jin D S 2010 Phys. Rev. Lett. 104 030402
5 Zhang Y C Ma J Wu J Z Wang L R Xiao L T Jia S T 2013 Phys. Rev. A 87 030503(R)
6 Li Y Q Feng G S Xu R D Wang X F Wu J Z Chen G Dai X C Ma J Xiao L T Jia S T 2015 Phys. Rev. A 91 053604
7 Ma J Wu J Z Chen G Fan Q C Feng H Dai X C Sun W G Xiao L T Jia S T 2013 J. Phys. Chem. Lett. 4 3612
8 Hummon M T Yeo M Stuhl B K Collopy A L Xia Y Ye J 2013 Phys. Rev. Lett. 110 143001
9 Stuhl B K Hummon M T Yeo M Quéméner G Bohn J L Ye J 2012 Nature 492 396
10 Brown W G Gibson G E 1932 Phys. Rev. 40 529
11 Curtis W E Patkowski J 1934 Phil. Trans. Roy. Soc. 232 395
12 Townes C H Merritt F R Wright B D 1948 Phys. Rev. 73 1334
13 Slotterback T J Clement S G Janda K C Western C M 1995 J. Chem. Phys. 103 9125
14 Durand A Loison J C Vigué J 1997 J. Chem. Phys. 106 477
15 Slotterback T J Clement S G Janda K C Western C M 1994 J. Chem. Phys. 101 7221
16 Townes C H Schawlow A L 1995 Microwave Spectroscopy New York McGraw-Hill
17 Herzberg G 1967 Molecular Spectra and Molecular Structure. I. Spectra of Diatomic Molecules Princeton D. Van Nostrand Company
18 Aldegunde J Rivington B A Żuchowski P S Huston J M 2008 Phys. Rev. A 78 033434
19 Aldegunde J Ran H Huston J M 2009 Phys. Rev. A 80 043410
20 Carrington A Howard B J Levy D H Robertson J C 1968 Mol. Phys. 15 187
21 Edmonds A R 1960 Angular Momentum in Quantum Mechanics Princeton Princeton
22 Curl R F Jr Kinsey J L 1961 J. Chem. Phys. 35 1758
23 Herbst E Steinmetz W 1972 J. Chem. Phys. 56 5342