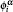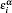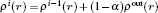† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant No. 2011CB606402) and the National Natural Science Foundation of China (Grant No. 51071091).
Further developments in the hybrid multiscale energy density method are proposed on the basis of our previous papers. The key points are as follows. (i) The theoretical method for the determination of the weight parameter in the energy coupling equation of transition region in multiscale model is given via constructing underdetermined equations. (ii) By applying the developed mathematical method, the weight parameters have been given and used to treat some problems in homogeneous charge density systems, which are directly related with multiscale science. (iii) A theoretical algorithm has also been presented for treating non-homogeneous systems of charge density. The key to the theoretical computational methods is the decomposition of the electrostatic energy in the total energy of density functional theory for probing the spanning characteristic at atomic scale, layer by layer, by which the choice of chemical elements and the defect complex effect can be understood deeply. (iv) The numerical computational program and design have also been presented.
The key problem in multiscale science is how to construct the model and to present the algorithm, both of which are involved in the physical connotation and the computational technique, as well as the related challenging problems — particularly for complex materials systems, including structural defects and chemical doping. A schematic pattern of multiscale is shown in Fig.
To exploit the physics spanning multiscale and multilevel, the development of new approaches is required, which should overstep the sequential multiscale model that suits the multiscale weakly coupling systems, [ 2 – 4 ] while the multiscale correlation in a not-too-weak coupling system must be studied using the unifying model, based on, for examples, quantum mechanics (QM), molecular dynamics (MD), and finite elements (FM) methods. In order to treat the problem, the hybrid scheme is presented to drive progress, some examples are given in the reference papers. [ 5 – 10 ] One of the characteristics of the hybrid multiscale methods lies in coupling between quantum mechanics and molecular mechanics, some related papers have been published, [ 7 – 9 ] which have important scientific significance and application potential.
Considering the multiscale requirement of the physical connotation and the mathematical treatment method, the hybrid energy density method published [ 11 – 15 ] must be developed further. In the present paper, we first focus on the study to obtaining the coupling weight parameter in the energy coupling equation of the multiscale transition region. The second study is to decompose the non-homogeneous charge density into the lattice sites in the complex physical system according to the structural characteristics. In order to solve these problems, new physical thought and new computational method will be introduced. Then the total energy of the complex physical system should be expressed in the form of the sum of the site energies.
The total energy can be expressed as the sum of the band energy and the electrostatic term, the expressions are written as follows: [ 11 , 16 , 17 ]




Equation (
A theoretical model is presented for treating the coupling between the electronic effect of the local region and the classical influence of the long range environment. The weighting coupling energy expression in the transition region has been represented [ 11 , 12 ] by the site energy as follows:

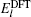
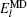
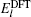
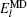
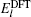
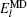
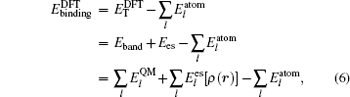
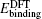
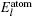
Then we can define an expression as follows:

The expression of energy coupling with weighting parameters of the entire system is constructed by site energy as follows:



In the present work, in order to obtain ω l ( l ∈ TR), the improvement for evaluating ω l is presented, we will compute ω l ( l ∈ TR) through an underdetermined system of linear equations.
As shown schematically in Fig. 

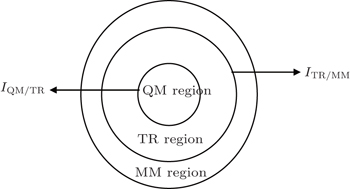 | Fig. 2. Schematic representation of a spatially partitioned system which contains three regions. There are two interfaces: I QM/TR between regions QM and TR, and I TR/MM between regions TR and MM. |
The energy of regions QM and TR 

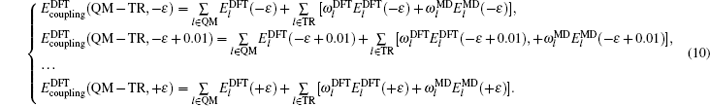

In the EDM, the forces are calculated by differentiating Eq. (


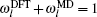

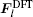
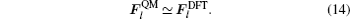

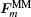
In the same way, the ionic force of the n -th site in the TR region can be computed as

The flowchart of the EDM is shown in Fig.
The EDM is performed in a model that measures 35.2 Å × 35.2 Å × 105.6 Å with 12000 atoms in total. The x , y , and z axes correspond to [010], [001], and [100], respectively, and the periodic boundary conditions are applied in the x and y directions as shown in Fig.
Next, we will determine the critical dimension of the TR region. The dimension of the TR region should be large enough so that 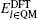

The DFT calculations are applied to both QM and TR regions with periodic boundary conditions in the x and y directions and a 12 Å vacuum layer in the z direction, as shown in Fig.
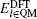
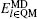
In the TR region, atoms in the same (100) layer share the same site energy and weighting parameter ω l . 

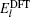

The 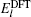
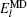
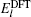
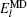

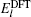

Based on the solution of the underdetermined equation, the weighting parameters are plotted in Fig.
The charge density of the EDM relaxed structure is calculated, and the results are plotted in Fig. 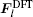

The key to the development of this theoretical algorithm lies in the decomposition of the electrostatic energy of the system into each atomic site, which can be predicted to realize the spanning scale correlation at the atomic scale layer-by-layer with the site energy; [ 11 , 13 ] then the information relevant to the choice of chemical elements and the control of defects may be provided for the problem of the electron behavior on atomic scale in the multiscale problems.
The Kohn–Sham equation based on local spin density approximation (LSDA) can be represented as
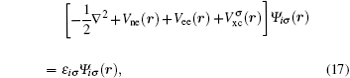
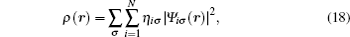







The ground state energy of the system is given by using Born–Oppenheimer approximation within the framework of density functional theory




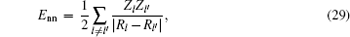
Based on the analytic expression of the total energy of the computational system and the design of the numerical calculation program, we introduce a new parameter and define




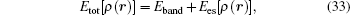




Based on the discrete variational method, [ 25 ] we can express an arbitrary 3D integration of multi-center function in the form of a weight summation of 3D quasi-random points

In order to realize the decomposition of the electrostatic energy of the system into each atomic site, it is necessary to partition 3D quasi-random points on each atomic region according to a Wigner–Seitz-like cell, and then correspondingly, the Coulomb energy and exchange–correlation energy will be partitioned on each atomic site, so that the total energy of the system can be written as


We adopt an efficient 3D integration method called Diophantine method proposed by Ellis [ 26 , 27 ] to calculate the electrostatic energy, where the integration of the electrostatic energy density within each Wigner–Seitz-like cell determines the part partitioned to each atom. The idea of the Diophantine method is using a weight summation of 3D quasi-random points to calculate the integration of the multi-center function. Considering the intense (smooth) variation of the electrostatic energy in the region close to (away from) the nucleus, especially the singularity at the nucleus, the 3D sample points are mostly concentrated in the region close to the nucleus. A distribution function D ( r ), which is the linear combination of Fermi-like function d v ( r ) centered in nucleus, is constructed to ensure the above consideration


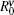
The integration weight ω ( r i ) (in Eq. (

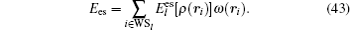
The development of theoretical computational methods has been proposed for treating the non-homogeneity of charge density systems with multi-alloying elements and a defect complex. We constructed the underdetermined equations for solving the weight parameters in the transition region of the energy coupling equation of the multiscale model and successfully used the equations to study the system of the homogeneous distribution of charge density. The theoretical algorithm for decomposing the electrostatic energy in the total energy of DFT into site energy has been proposed. The numerical computational program has been written.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 |