Entropy and heat generation of lithium cells/batteries
[Wang Songrui †, 
]
]
Cite this Article 
Wang Songrui. Entropy and heat generation of lithium cells/batteries. Chinese Physics B , 2016, 25(1): 010509 
Permissions
Entropy and heat generation of lithium cells/batteries
Abstract
Abstract
The methods and techniques commonly used in investigating the change of entropy and heat generation in Li cells/batteries are introduced, as are the measurements, calculations and purposes. The changes of entropy and heat generation are concomitant with the use of Li cells/batteries. In order to improve the management and the application of Li cells/batteries, especially for large scale power batteries, the quantitative investigations of the change of entropy and heat generating are necessary.
PACS :
05.70.–a
1. Introduction
In the laws of thermodynamics, Gibbs energy is the maximum possible nonexpansion work output done by a closed system under a process with constant temperature and pressure. In a closed electrochemical system, nonexpansion work output is electric energy, so when the chemical energy is converted into electric energy under a reversible process, the electric energy equals the Gibbs energy, i.e., Δ G = – nFE . When the chemical energy is converted into electric energy under an irreversible process, the electric energy is less than the Gibbs energy, i.e., nFE < –Δ G . The residual Gibbs energy is converted into heat energy. [ 1 ]
In the second law of thermodynamics, entropy is an extensive state function under a reversible process: d S ≡ d q / T , so under a reversible process, with constant temperature and pressure
Based on the laws of thermodynamics, the theoretical potential of an electrochemical system can be calculated from the Gibbs energy data, and the maximum electric energy that can be delivered by the chemicals that are stored within or supplied to the electrodes in the cell depends on the change in Gibbs energy Δ G of the electrochemical couple. The open potential of a cell can be obtained experimentally and is less than or equals to the theoretical potential. Both the theoretical potential and the open potential are determined by the type of electrochemical couples and the electrolyte contained in the cell.
In a practical cell, it is desirable that all of the Gibbs energy can be converted to useful electric energy during discharge. However, energy losses due to polarizations occur when a load current passes through the cell, accompanying the electrochemical reactions.
The most important factor that affects the energy losses of a cell is the polarizations. The total polarizations of a cell include: ( i ) Ohmic polarization, which causes the voltage drop during operation, and also consumes part of the useful energy as waste heat. The total ohmic polarization of a cell is the sum of the polarizations caused by the ionic resistance of the electrolyte, the electronic resistances of the electrodes, the current collectors and electrical tabs of both electrodes, and the contact resistance between the active materials and current collectors. The Ohmic polarization follows Ohm’s law, with a linear relationship between the current and the voltage drop. (ii) activation polarization, which drives the electrochemical reaction at the electrode/electrolyte interface, and (iii) concentration polarization, which appears due to the concentration differences between the reactants and the products at the electrode/electrolyte interface and the concentration differences in the bulks as a result of mass transferring.
All these polarizations cause consumption of Gibbs energy, which is given off as heat energy during the charge–discharge process.
In lithium cells, the active materials are porous, allowing lithium ions to be inserted in or extracted from them during the charge–discharge process, so the polarizations of a lithium cell are more complex and the heat generation in lithium cells is also more complex due to heat being generated with each physical process.
Lithium cells have high specific energy, so the Gibbs energy in cells is high. They will generate high heat energy accompanying the conversion process from Gibbs energy into useful electric energy. If such heat energy cannot be dispersed, the temperature of a closed lithium cell/battery increases, which may influence the performance of the cell/battery.
Furthermore, because of the high Gibbs energy in lithium cells, if side reactions occur, more heat energy is converted from the Gibbs energy, increasing the temperature. When the temperature of lithium cells is high enough to induce decomposition of electrodes or electrolytes, an accident may happen.
Therefore, the investigations of entropy in lithium cells have focused on evaluating the heat and estimating the degradation of cells, because entropy is an extensive state function. The investigations of heat in lithium cells have focused on evaluating and measuring the heat. Based on evaluating the heat and measuring accurately, the management and guidance of lithium cells/batteries/systems could be operated smoothly and accidents could be fewer. [ 2 ]
2. Entropy
2.1. Entropy determination
According to the laws of thermodynamics, in a closed electrochemical system Δ S = –Δ G / T = nF ( E / T ), so the change of entropy (Δ S ) can be obtained through the slope of the open-circuit voltage (OCV) with temperature. The change of entropy commonly can be determined by a potentiometric method. [ 3 ] In such a method, the cell is discharged to a desired state of charge (SOC), and after a relaxation, the open circuit voltage goes to equilibrium, then the cell undergoes a step by step temperature variation, during which the open circuit voltage is monitored. Typical results of the potentiometric method include a curve of the corresponding OCVs as functions of temperature and a line of the slope of the OCV versus temperature plot (Fig.
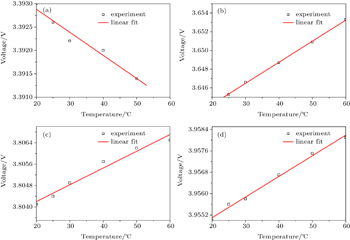 | Fig. 1. The curves of the corresponding OCVs as a function of the temperature for NCA/C cells at different SOCs. (a) SOC=0.122; (b) SOC=0.458; (c) SOC=0.644; (d) SOC=0.813. |
Recently, Schmidt et al . developed an electrothermal impedance spectroscopy method to determine the change of entropy, in which the measurement times can be 100 times shorter than in a potentiometric method. [ 4 ] The accuracy of this method is similar to that of a potentiometric method. In electrothermal impedance spectroscopy, the relationship between heat flow inside the cell and the resultant temperature change can be exploited, employing a sinusoidal current source. When the thermal transfer function (thermal impedance) is known and the surface temperature is measured, the heat flow inside the cell can be calculated. The change of entropy (Δ S ) can be calculated through the linear function between the heat flow and multiplying the current and the entropy. The Δ S in LiFePO 4 cells determined by the conventional potentiometric method and by the electrothermal impedance spectroscopy have shown similar behaviors and are in good accordance. However, a hysteresis behavior of the Δ S has been observed, due to the superposition of the charging and discharging current.
2.2. Application in heat evaluation
The heat generation of lithium cells during the charge and discharge process can be attributed to two main sources: the reversible heat and the irreversible heat. The irreversible heat is complex and is described in different forms in different heat evaluating models, but the reversible heat is described consistently as Q rev = T Δ S = nFT ( E / T ) in all heat evaluating models.
In the typical electrochemical-thermal model, [ 5 ] the reversible heat generating rate is described as
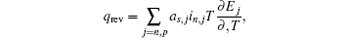
In the typical equivalent circuit–thermal model, [ 6 ] the reversible heat generating rate is described as
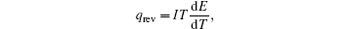
Therefore, the reversible heat generating rate can easily be calculated from the change of entropy or the change of d E /d T , easily.
2.3. Application in estimating degradation
If the states of electrode or electrochemical system change, the entropy must change concomitantly, because entropy is an extensive state function. Therefore, the change of entropy can be applied in characterizing the changes of electrode structures and estimating the state of a cell/battery. Yazami et al . investigated the entropy curve and the crystal structure of lithium-intercalated graphite. [ 7 , 8 ] The entropy curve shows a sharp re-increase at x = 0.5 in Li x C 6 , responding to the transition from a well-ordered stage-2 compound LiC 12 to a well-ordered stage-1 compound LiC 6 , and the occurrence of intermediary phase(s) between the two lithium-rich intercalation stages is confirmed by in situ XRD and the Raman spectra, during lithium ion intercalating into graphite. Besides, the negative value of the entropy of intercalation at x > 0 : 25 in Li x C 6 is explained by the vibrating frequency of lithium atoms in graphite being higher than that in lithium metal. Lu et al . investigated the changes of entropy of LiMn 2 O 4 , Li 1.156 Mn 1.844 O 4 , and Li 1.06 Mn 1.89 Al 0.05 O 4 spinel cathode materials in half-cell systems. [ 9 ] The results show that the entropy profiles of the different spinel cathodes during cycling correlated well with the phase transition and the order/disorder changes.
Furthermore, Mahera and Yazamia developed a method to estimate the state of degradation of lithium ion cells through the entropy and the thermodynamics behavior. They investigated the effects of overcharge, cycle aging and thermal aging on the entropy of lithium-ion batteries using lithium cobalt oxide cathodes and graphite anodes. The entropy varies dramatically with the applied cut-off voltage (4.2 V–4.9 V). These changes correlate well with the crystal structure degradations of the cathode and the anode. [ 10 ] With increasing cycle number, the entropy shows more significant changes than those observed in the discharge and the open-circuit potential curves especially at particular states of charge and open-circuit potential values. These differences are attributed to the higher sensitivity of entropy state functions to changes in the crystal structure of the cathode and the anode induced by cycle aging. [ 11 ] In addition, the entropy shows more obvious changes with the ageing time than the open-circuit potential, when cells are stored at 60 °C and 70 °C. [ 12 ] So they suggest that entropy can be used to characterize the degradation level of electrode materials and consequently assess the cell’s state of health (SOH). Furthermore, Wu et al. suggest that differential thermal voltammetry (d T /d V ) can be used for tracking degradation in lithium-ion batteries. [ 13 ]
3. Heat generation
The major investigations of heat generation are the studies on the processes and mechanisms, in addition to the side reactions (decomposition reactions) in lithium cells and the heat energy converted from the Gibbs energy in each physical process and electro-chemical process.
3.1. Charge–discharge process
Heat evaluation is necessary to manage the thermal behavior of the battery in scaled-up systems, and to improve the efficiency of the cooling systems. Quantitative measurements and heat calculations are useful ways of evaluating heat.
3.1.1. The quantitative measurements of heat generation
The accelerated rate calorimeter (ARC), [ 14 – 17 ] the heat conduction calorimeter [ 18 ] and the isothermal calorimeter [ 19 ] have been used in investigations of heat generation during charge–discharge. In the ARC test, no heat is lost to the surroundings, and so all the reaction energy released concerns only the battery’s self-heating. On the other hand, in both the heat conduction calorimeter and the isothermal calorimeter, the heat generated during charge–discharge is transferred quantifiably. Quantitative measurements of heat generation of lithium cells are important for thermal management of scaled-up battery systems.
Selman et al. measured Panasonic (type CGR 18650H), Sony (type US18650), A&T (type 18650) and x-18650 (LiCo 0.2 Ni 0.8 O 2 and graphite as the cathode and the anode, respectively) cells at C/6 charge/discharge rate, employing ARC. [ 14 ] Saito measured Sony (type US14500, LiCoO 2 and hard carbon as the cathode and the anode, respectively) cells at C/5 discharge rate, using a twin-type heat conduction calorimeter. [ 18 ]
3.1.2. Heat calculations 
Calculations of heat during charge–discharge are obtained though models of lithium cells/batteries. Among them, the equivalent circuit–thermal models and the electrochemical-thermal models are the most common.
In the equivalent circuit–thermal models, lithium cells are represented by circuits consisting of traditional electrical components. The heat generated during charge–discharge is separated into reversible heat ( Q rev ) and irreversible heat ( Q irrev ). The reversible heat ( Q rev ) is calculated by the change of entropy (Δ S ): Q rev = T Δ S = nFT ( E / T ), as discussing above. There are two common methods to calculate the irreversible heat ( Q irrev ). [ 20 , 21 ] One is calculated through ohmic heat: Q irrev = I 2 R , in which R changes with the changing of the states of cells, the operation and the environment conditions, such as SOC, cycles, current density, temperature, etc. [ 20 ] Another method is to calculate through the energy conservation and the voltage: Q irrev = nF ( E the – E cur ), in which E the is the theoretical potential of the cell system and E cur is the actual potential with current. [ 21 ] The heat calculations through the equivalent circuit–thermal models are concise, so it has been used in most heat management systems, and the accuracy of results depends on the elaborateness of the models.
Choi et al. calculated the heat generation of lithium ion cells used in hybrid electric vehicle (HEV) systems, in order to develop a simple model to describe the thermal behavior of an air-cooled Li-ion battery system, proposed from a vehicle component designer’s point of view. [ 20 ] Walker et al. calculated the heat generation of lithium ion cells for space applications, and coupled it with specialized orbital-thermal software, thermal desktop (TD), to simulate the temperature versus depth-of-discharge (DOD) profiles and temperature ranges for all discharge and convection variations with minimal deviation. [ 18 ] Srinivasan et al. developed a model to calculate heat generation through five different internal parameters: the electrolyte resistance ( R s ), anode resistance ( R a ), cathode resistance ( R c ), and entropy changes in the cathode (Δ S c ), and the anode (Δ S a ). [ 22 ] These five parameters are not dependent upon each other; they are dependent on the state of charge and the environmental temperature. Hariharan developed a nonlinear equivalent circuit model for lithium ion cells using variable resistors, which are functions of the cell temperature. The model can be used to predict the cell voltage and temperature over a wide range of powers with a global set of parameters. [ 6 ]
In electrochemical–thermal models, the charge–discharge process is separated into many physical and chemical processes, for example, the diffusion of lithium ion in liquid and solid, the transfer of lithium between liquid and solid, the polarization on the surface of electrodes, etc. The heat generated during charge–discharge is the heat effect of each physical and chemical process, which commonly can be calculated as [ 23 ]
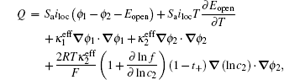
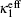
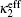
The calculation of heat generated during charge–discharge based on electrochemical–thermal models is very complex, so it is used in theoretical research, but not commonly in applications.
Kumaresan et al . developed a thermal model for LiCoO 2 /MCMB lithium ion cells to predict the discharge performance at different temperatures (15–45 °C). [ 21 ] Pals and Newman developed a one-dimensional thermal model for a lithium/polymer cell to predict the temperature profile in a Li/PEO 15 -LiCF 3 SO 3 /TiS 2 cell stack discharge at 3 h rate. [ 24 ] Baba et al . developed an enhanced single-particle model to understand the thermal behavior of lithium-ion cells and distribute information related to local heat generation across the entire electrode plane, and a two-way electrochemical–thermal coupled simulation method has also been established. [ 5 ]
3.1.3. Application in management systems
Heat/temperature management is one important part of the management systems of lithium batteries. The heat generation of lithium cells during charge–discharge is the basis for the heat/temperature management. Giuliano et al. showed that a liquid-cooled system is a viable option for the thermal management. [ 25 ] And the cooling system is easily able to cool the batteries and approach a steady state well below the maximum operating temperature. Tong et al. developed an active thermal management system comprising forced liquid cooling, on the base of the electrochemical and thermal behavior of a bipolar battery. [ 26 ] Higher coolant velocity and coolant plate thickness are helpful in keeping the maximum temperature and temperature non-uniformity under control; however, this approach increases the parasitic load as well as the weight and volume of the pack.
3.2. Thermal runaway
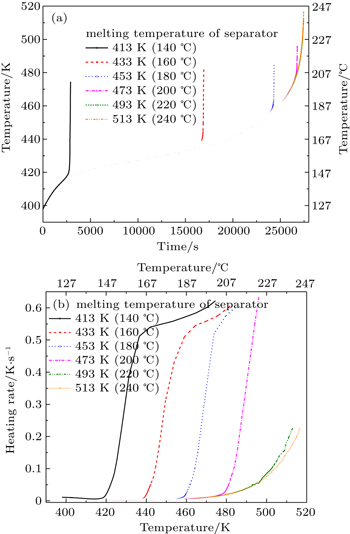
In an accident, the chemical energy in electrodes may convert into heat energy rather than electric energy, which can induce lithium cells into thermal runaway. [ 27 ] There are a few factors that can lead lithium cells into thermal runaway, among which the temperature of the lithium cell is one of the key determinants. The investigations of heat generation during thermal runaway can be used to predict the safety and the criticality of lithium cells/batteries.
The heat generation during thermal runaway can be measured by calorimeters that can endure the explosion of lithium cells such as ARC (Fig.
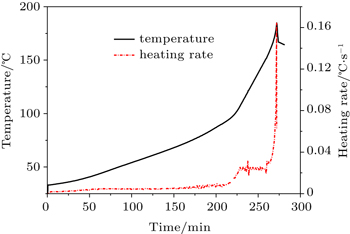 | Fig. 2. The curves of thermal runaway process for a LiNi 0.5 Mn 1.5 O 4 /C cell in an ARC experiment. |
 | Fig. 3. The simulation results of LiFePO 4 /C cells using separators with different melting temperature, (a) the simulation results of temperature curves; (b) the simulation results of heating rate curves. |
The calculations of heat generated during thermal runaway process are commonly based on the thermal behavior of materials in the lithium cell. The results of calculations can be used to study the origin and the effects of thermal runaway, in order to improve the safety design of lithium cells.
Richard et al . proposed a model for the thermal runaway of a 18650 carbon/Li 1+ x Mn 2– x O 4 lithium-ion cell, based on the thermal stability of de-intercalated Li 1+ x Mn 2– x O 4 and lithium intercalated MCMB electrodes in LiPF 6 EC:DEC electrolyte. [ 29 ] The model has been used to predict the short-circuit behavior and the oven exposure behavior of the cell. The results agree qualitatively with that of experiments. Kim et al. extended the one-dimensional modeling approach formulated by Hatchard et al. [ 30 ] to three dimensions. The calculation results of oven abuse testing of cells with cobalt oxide cathode and graphite anode with LiPF 6 electrolyte show that thermal runaway will occur sooner or later than the lumped model, depending on the size of the cell, and the reactions initially propagate in the azimuthal and longitudinal directions to form a hollow cylinder-shaped reaction zone. [ 31 ] Wang et al. calculated heat generated during thermal runaway of LiFePO 4 /C cells, and the results show that the inner short circuit, caused by the melting down of the separator, is the major factor of thermal runaway of such cells, in which the separator with a lower melting-down temperature has been used. However, when the LiFePO 4 /C cell employs a separator with a higher melting down temperature, decomposition reactions of electrode material become the major factor of safety. [ 32 ]
4. Conclusion
The changes of entropy and heat generation of lithium cells are ineluctable. Investigations of them are a part of the research into lithium cells. Understanding the change of entropy and heat generation can benefit the study of the state and the safety of lithium cells. The quantification of the change of entropy and heat generation can improve the level of management and control for security of lithium cells/batteries.
Reference
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 |