Cite this Article
Wu Qin. Tunable ponderomotive squeezing induced by Coulomb interaction in an optomechanical system. Chinese Physics B , 2016, 25(1): 010304  
Permissions
Tunable ponderomotive squeezing induced by Coulomb interaction in an optomechanical system
Wu Qin †,
School of Information Engineering, Guangdong Medical University, Dongguan 523808, China

 

† Corresponding author. E-mail: 905374532@qq.com

Abstract
Abstract

We investigate the properties of the ponderomotive squeezing in an optomechanical system coupled to a charged nanomechanical oscillator (NMO) nearby via Coulomb force. We find that the introduction of Coulomb interaction allows the generation of squeezed output light from this system. Our numerical results show that the degree of squeezing can be tuned by the Coulomb coupling strength, the power of laser, and the frequencies of NMOs. Furthermore, the squeezing generated in our approach can be used to measure the Coulomb coupling strength.

PACS : 03.67.–a ; 42.50.Lc ; 46.80.+j
Keyword : ponderomotive squeezing ; Coulomb interaction ; optomechanical system
1. Introduction

The optomechanical system has sparkled the interest of a vast scientific community due to its distinct applications, ranging from sensing of masses, forces, and displacements at the ultimate quantum limits, to tests of the validity of quantum mechanics at a macroscopic level, up to the realization of quantum interfaces for quantum information networks. [ 1 – 4 ] In a typical optomechanical system, the coupling between a movable mirror and the cavity field can lead to many remakable effects, such as the optomechanically induced transparency (OMIT), [ 5 – 11 ] the quantum ground state cooling of the nanomechanical resonators, [ 12 – 14 ] entanglement between cavity modes and/or mechanical modes, [ 15 – 22 ] and squeezed states of the light or the mechanical modes. [ 23 – 25 ]

On the other hand, the squeezed light, where fluctuations in one quadrature of the optical amplitude drop below the level of vacuum noise, is interesting from both fundamental and practical points of view. Such light can be used to improve the measurement sensitivity in applications ranging from gravitational wave detection [ 26 ] to even biological measurements. [ 27 ] Squeezed states of light are also a key ingredient for continuous-variable information processing. [ 28 ] It is well known that the standard method for generating optical squeezing is to drive a nonlinear optical medium, [ 29 ] which has been realized in Ref. [ 30 ]. Recently, the squeezing of the transmitted field can also be achievable in optomechanical systems, [ 31 , 32 ] where cavity photons are coupled to mechanical motion by radiation pressure. The optomechanical method of manipulating the quantum fluctuations has been termed as “ponderomotive squeezing”, [ 30 ] which relies on the nonlinearity induced by the optomechanical interaction between the position of the oscillator and the intensity of the cavity mode. [ 31 , 33 ] Moreover, achieving this kind of ponderomotive squeezing experimentally is an important goal due to its applications in ultrahigh precision measurements. [ 34 – 36 ]

In this work, we demonstrate a tunable squeezed light observable in an optomechanical system, in which the two nanomechanical oscillators (NMO) are coupled through Coulomb force. We find that the single peak in squeezing spectrum is split to two peaks due to the Coulomb interaction. Specifically, the separation of the two optimal squeezing points can be tuned by the Coulomb interaction.

Compared to previous studies, [ 37 , 38 ] where the ponderomotive squeezing is generated in a cavity assisted by an atomic ensemble or in a ring cavity consisting of two mirrors without Coulomb force, our scheme owns some favorable features. First, the squeezed light generated in our scheme is created by Coulomb interaction. In addition, the Coulomb coupling has important advantages, for instance, the range of the interaction distance is from nanometer to meter, [ 39 – 41 ] the strength can be controlled by the bias voltage, [ 39 , 40 ] and it can also be applied to the different kinds of charged objects at different frequecies. [ 41 ] Second, the point with optimal squeezing can be tuned by the frequencies of the two NMOs. Finally, we find that the two optimal squeezing points are apart near linearly with respect to the Coulomb coupling strength. This feature reminds us of a practical application of the ponderomotive squeezing spectrum for detecting the Coulomb coupling strength. In this context, we have to emphasize that our proposal is essentially different from previous idea, [ 38 ] where the squeezed light is caused by the frequency difference between the two movable mirrors. In contrast, our studied squeezed light can be observed even for two identical movable mirrors.

The remainder of this paper is organized as follows. In Section 2, we present the model under study and analytical expressions of the optomechanical system, derive the quantum Langevin equations, and the steady state of the system. In Section 3, we quantify the squeezing properties of the system. Finally we draw our conclusions in Section 4.

2. Model and solution

As sketched in Fig.  1 , our system consists of a high-quality Fabry–Pérot cavity with a fixed mirror and a nanomechanical oscillator NMO 1 . NMO 1 with the bias gate voltage V 1 is coupled to another charged NMO 2 with the bias gate voltage − V 2 through the Coulomb force. The optomechanical cavity of the length L is driven by one strong pump field ɛ p from the left side of the cavity. The output field is represented by ɛ out . q 1 and q 2 represent the small displacements of NMO 1 and NMO 2 from their equilibrium positions, and r 0 is the equilibrium distance between the two NMOs. Then, the Hamiltonian in the rotating frame at frequency of the pump field ω p can be written as

where Δ c = ω c − ω p is the detuning of the pump field from the bare cavity. The first term in Eq. ( 1 ) is for the single-mode cavity field with frequency ω c and annihilation (creation) operator c ( c † ). The second (third) term describes the vibration of the charged NMO 1 (NMO 2 ) with frequency ω 1 ( ω 2 ), effective mass m 1 ( m 2 ), the position q 1 ( q 2 ), and the momentum operator p 1 ( p 2 ). [ 42 ] NMO 1 couples to the cavity field due to the radiation pressure with the coupling strength . The fifth term in Eq. ( 1 ) presents the Coulomb coupling between the charged NMO 1 and NMO 2 , [ 41 ] where the NMO 1 and NMO 2 take the charges Q 1 = C 1 V 1 and Q 2 = − C 2 V 2 , with C 1 ( C 2 ) and V 1 (− V 2 ) being the capacitance and the voltage of the bias gate, respectively. The last term in Eq. ( 1 ) describes the interaction between the cavity field and the input field. The pump field strength ɛ p depends on the power ℘ p of coupling field, , where κ is the cavity decay rate.

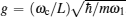
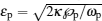
Schematic diagram of the system.

Using the Heisenberg equations of motion, and considering photon losses from the cavity and the Brownian noise from the environment, we can obtain the following nonlinear quantum Langevin equations for the operators of the mechanical and optical modes: [ 42 ]

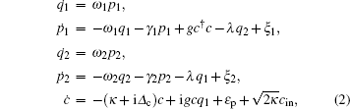
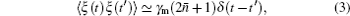
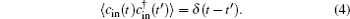
where γ 1 ( γ 2 ) and κ are the decay rates for NMO 1 (NMO 2 ) and the cavity, respectively. The quantum Brownian noise ξ 1 ( ξ 2 ) comes from the coupling between NMO 1 (NMO 2 ) and its own environment with correlation function [ 43 ]

where n̄ = [exp( ħ ω m / k B T ) − 1] −1 is the mean number of thermal excitation, with k B being the Boltzmann constant. The c in is the input vacuum noise operator with correlation function [ 43 ]

We can rewrite each Heisenberg operator as a steady-state value plus an additional fluctuation operator with zero-mean value, c = c s + δ c , q i = q i s + δ q i , p i = p i s + δ p i ( i = 1,2). Then we insert these expressions into the Langevin equations and obtain the steady-state values

where Δ = Δ c − gq 1s is the effective cavity detuning.

Retaining only first-order terms in the small quantities δ o ( o = c , q i , p i ), the linearized Langevin equations for the fluctuations are given by

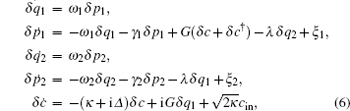
where G = gc s is the effective coupling strength.

It is more convenient to work in the frequency domain because, experimentally, fluctuations of the electric field are more convenient to be measured in the frequency domain than in the time domain. Using the following Fourier transform for an operator u ( u = δc , δ p i , δ q i , c in , and ξ i ),

we rewrite Eq. ( 6 ) in the frequency domain in matrix form

where

in which we have defined Θ 1 = κ + i ω + i Δ and Θ 2 = κ + i ω − i Δ .

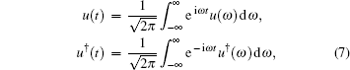
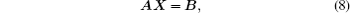
By solving Eq. ( 8 ), we obtain

where the coefficients are given by

in which we have defined

In the following, we will study the ponderomotive squeezing numerically in the frequency domain.

3. Ponderomotive squeezing

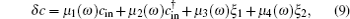
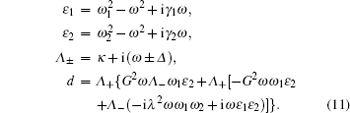
It was shown that the optomechanical coupling can lead to squeezing of the nanomechanical motion, which can be inferred by measuring the squeezing of the transmitted microwave field. Here we analyze the squeezing properties of the transmitted field, which is accessible to experiment and useful for practical applications. [ 34 – 36 ] The squeezing spectrum of the transmitted field is given by [ 32 ]

where and . By using the results of Eqs. ( 9 ) and the following correlation functions in the frequency domain:

we can obtain

in which

Taking Eq. ( 14 ) into Eq. ( 12 ), we can obtain the squeezing spectrum in a simple form

As the phase angel θ is an adjustable parameter, we choose appropriate θ by solving d S θ ( ω )/(d θ ) = 0, then we obtain

Here, we choose the negative value to optimize the degree of squeezing. Hence, equation ( 16 ) can be rewritten as

In order to obtain squeezing, the term 2 B c † c − 2| B cc | in the right-hand side must be negative, i.e., S opt ( ω ) < 1.

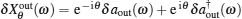
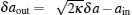
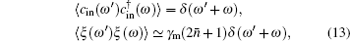
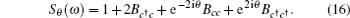
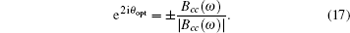
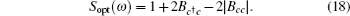
For simplicity, we first assume two identical charged NMOs ω 1 = ω 2 = ω m and the detuning between the pump field and the cavity mode satisfying Δ ≃ ω m . To demonstrate the numerical results, we use the experimentally realizable parameters from Refs. [ 44 ] and [ 45 ]: λ c = 1064 nm, κ = π × 10 7  Hz, ω m = 2 π × 10 7  Hz, γ 1 = γ 2 = 400 π  Hz, L = 6 mm, m 1 = m 2 = 12 ng.

Firstly, we discuss the dependence of ponderomotive squeezing on the Coulomb interaction strength (units of λ 0 = π × 10 7  Hz/m 2 ) in Fig.  2 , where we have set T 1 = 2 mK, T 2 = 3 mK, and ℘ p = 10 mW. One can find from this figure that the squeezing spectrum presents only a single peak at the frequency ω = ω m in the absence of the Coulomb interaction ( λ = 0), and the single peak is split into two peaks in the presence of the Coulomb coupling. This is due to the fact that an additional hybrid energy level is introduced into the original three-level system by the Coulomb coupling between the external NMO and the optomechanical resonator, which is quite different from Ref. [ 38 ]. The introduction of Coulomb coupling also leads to a split in the OMIT window, as reported in Ref. [ 39 ]. Moreover, the two points ω L,R with optimal squeezing are further and further apart with the increase of λ . For example, ω L(R) = 0.93 ω m (1.06 ω m ), 0.86 ω m (1.12 ω m ), and 0.71 ω m (1.23 ω m ) for the case of λ = 0.25 λ 0 , 0.5 λ 0 , and λ = λ 0 , respectively. Obviously, the separation d = ω R − ω L is 0.52 ω m when λ = λ 0 , which is about twice of that in the case of λ = 0.5 λ 0 . In order to further explore the influence of Coulomb interaction on the separation d , we plot d as a function of the coupling strength λ (units of λ 0 = π × 10 7  Hz/m 2 ) in Fig.  3 , where the separation d almost linearly increases with λ within the regime λ = {0, 1.6 λ 0 }. This indicates the possibility to detect the Coulomb coupling strength between NMO 1 and NMO 2 by measuring the separation d in the squeezing spectrum of the output field. We also find that the degree of squeezing at point ω = ω L ( ω R ) increases (decreases) with the Coulomb coupling strength.

The squeezing spectrum with different Coulomb coupling strength λ when ℘ p = 10 mW, T 1 = 2 mK, T 2 = 3 mK. (a) λ = 0; (b) λ = 0.25 λ 0 ; (c) λ = 0.5 λ 0 ; (d) λ = λ 0 ( λ 0 = π × 10 7  Hz/m 2 ).

Then we show the effect of the power of pump field on the degree of squeezing in Fig.  4 . Comparing Fig.  2(c) and Fig.  4 , we can find that the degree of squeezing is enhanced with increasing power of pump field, while there is no effect on the separation of the two optimal squeezing points. This is due to the fact that a larger power will input more photons which will effectively overcome the effects of the thermal noise.

Separation between two optimal squeezing points as a function of the Coulomb coupling strength λ (units of λ 0 = π × 10 7  Hz/m 2 ) when ℘ p = 10 mW, T 1 = 2 mK, and T 2 = 3 mK.

Finally, we consider the ponderomotive squeezing with non-identical NMOs since the two identical NMOs considered above are theoretically simplified but rarely existing experimentally. For two charged NMOs with different frequencies, as plotted in Fig.  5 , where we have set the frequencies of NMOs ω 1 = ω m ± 0.1 × 2 π × 10 7  Hz and ω 2 = ω m ∓ 0.1 × 2 π × 10 7  Hz, the degree of squeezing at the optimal squeezing points changes with respect to the case of identical NMOs. That is to say, the degree of squeezing at frequency ω L decreases while the degree of squeezing at frequency ω R is enhanced in case of ω 1 > ω 2 , as seen in Fig.  5(a) , but the opposite changes in degree of squeezing at these two points take place in case of ω 1 < ω 2 , as shown in Fig.  5(b) . Thus, this provides us a good method for controlling the degree of squeezing and finding the optimal squeezing.

Squeezing spectrum with different power of the pump field when λ = 0.5 λ 0 , T 1 = 2 mK, T 2 = 3 mK. (a) ℘ p = 5 mW; (b) ℘ p = 15 mW.

The squeezing spectrum with different frequencies of NMOs when λ = 0.5 λ 0 , ℘ p = 10 mW, T 1 = 2 mK, T 2 = 3 mK. (a) ω 1 = ω m + 0.1 × 2 π × 10 7  Hz, ω 2 = ω m − 0.1 × 2 π × 10 7  Hz; (b) ω 1 = ω m − 0.1 × 2 π × 10 7  Hz, ω 2 = ω m + 0.1 × 2 π × 10 7  Hz.

4. Conclusion

In conclusion, we analyzed the properties of the ponderomotive squeezing in an optomechanical system with two charged NMOs. We show that a squeezed light can be achievable in this system due to the introduction of Coulomb interaction between two NMOs. We also find that the degree of squeezing can be flexibly controlled by adjusting the Coulomb coupling strength, the laser power, and the frequencies of the two NMOs. In addition, we demonstrate the splitting of the two optimal squeezing points varies near linearly with the Coulomb interaction, which might be applied to measure the Coulomb coupling strength.

Reference
1 Kippenberg T J Vahala K J 2008 Science 321 1172
2 Marquardt F Girvin S M 2009 Physics 2 40
3 Verlot P Tavernarakis A Briant T Cohadon P F Heidmann A 2010 Phys. Rev. Lett. 104 133602
4 Mahajan S Kumar T Bhattacherjee A B ManMohan 2013 Phys. Rev. A 87 013621
5 Huang S Agarwal G S 2011 Phys. Rev. A 83 043826
6 Han Y Cheng J Zhou L 2011 J. Phys. B: At. Mol. Opt. Phys. 44 165505
7 Ma Y H Zhou L 2013 Chin. Phys. B 22 024204
8 Karuza M Biancofiore C Bawaj M Molinelli C Galassi M Natali R Tombesi P Diuseppe G Vitali D 2013 Phys. Rev. A 88 013804
9 Shu J 2011 Chin. Phys. Lett. 28 104203
10 Yan X B Yang L Tian X D et al. 2014 Acta Phys. Sin. 63 204201 (in Chinese)
11 Yan X B Gu K H Fu C B et al. 2014 Chin. Phys. B 23 114201
12 Rocheleau T Ndukum T Machlin C Hertzberg J Clerk A Schwab K 2010 Nature 463 72
13 Miao H Danilishin S Müller-Ebhardt H Chen Y 2010 New J. Phys. 12 083032
14 Liu Y C Xiao Y F Luan X S Wong C W 2015 Sci. China-Phys. Mech. Astro 58 050305
15 Yan Y Gu W J Li G X 2015 Sci. China-Phys. Mech. Astro. 58 050306
16 Vitali D Gigan S Ferreira A Böhm H R Tombesi P Guerreiro A Vedral V Zeilinger A Aspelmeyer M 2007 Phys. Rev. Lett. 98 030405
17 Palomaki T A Teufel J D Simmonds R W Lehnert K W 2013 Science 342 710
18 Joshi C Akram U Milburn G J 2014 New J. Phys. 16 023009
19 Liao J Q Wu Q Q Nori F 2014 Phys. Rev. A 89 014302
20 Ghobadi R Kumar S Pepper B Bouwmeester D Lvovsky A I Simon C 2014 Phys. Rev. Lett. 112 080503
21 Zheng Q Zhang D 2013 Chin. Phys. Lett. 30 024213
22 Wu Q Xiao Y Zhang Z M 2015 Chin. Phys. B 24 104208
23 Woolley M J Doherty A C Milburn G J Schwab K C 2008 Phys. Rev. A 78 062303
24 Sete E A Eleuch H 2012 Phys. Rev. A 85 043824
25 Asjad M Agarwal G S Kim M S Tombesi P Di Giuseppe G Vitali D 2014 Phys. Rev. A 89 023849
26 Abadie J Abbott B P Abott T D et al. 2011 Nat. Phys. 7 962
27 Taylor M A Janousek J Daria V Knittel J Hage B Bachor H A Bowen W P 2013 Nat. Photon. 7 229
28 Braunstein S L Van L P 2005 Rev. Mod. Phys. 77 513
29 Eberle T Steinlechner S Bauchrowitz J Händchen V Vahlbruch H Mehmet M Müller-Ebhardt H Schnabel R 2010 Phys. Rev. Lett. 104 251102
30 Braginsky V Manukin A 1967 Sov. Phys. JETP 25 653
31 Fabre C Pinard M Bourzeix S Heidmann A Giacobino E Reynaud S 1994 Phys. Rev. A 49 1337
32 Mancini E Tombesi P 1994 Phys. Rev. A 49 4055
33 Mancini S Mankó V I Tombesi P 1997 Phys. Rev. A 55 3042
34 Brooks D W C Botter T Schreppler S Purdy T P Brahms N Stamper-Kum D M 2012 Nature 448 476
35 Safavi-Naeini A H Gröblacher S Hill J T Chan J Aspelmeyer M Painter O 2013 Nature 500 185
36 Purdy T P Yu P L Peterson R W Kampel N S Regal C A 2013 Phys. Rev. X 3 031012
37 Xiao Y Yu Y F Zhang Z M 2014 Opt. Express 22 017979
38 Min F X Xiao X Y Yu Y F Zhang Z M 2015 Chin. Phys. B 24 050301
39 Ma P C Zhang J Q Xiao Y Feng M Zhang Z M 2014 Phys. Rev. A 90 043825
40 Chen R X Shen L T Zheng S B 2015 Phys. Rev. A 91 022326
41 Hensinger W K Utami D W Goan H S Schwab K Monroe C Milburn G J 2005 Phys. Rev. A 72 041405(R)
42 Agarwal G S Huang M 2012 Phys. Rev. A 85 021801(R)
43 Genes C Vitali D Tombei D Gigan S Aspelmeyer M 2008 Phys. Rev. A 77 033804
44 Kleckner D Marshall W de Dood Michiel J A Dniyari K N Pors B J Irvine W T M Bouwmeester D 2006 Phys. Rev. Lett. 96 173901
45 Teufel J D Li D Allman M S Cicak K Sirois A J Whittaker J D Simmonds K R W 2011 Nature 471 204