Project supported by the National Natural Science Foundation of China (Grant No. 61227902).
The laser-pumped potassium spin-exchange relaxation free (SERF) magnetometer is the most sensitive detector of magnetic field and has many important applications. We present the experimental results of our potassium SERF magnetometer. A pump–probe approach is used to identify the unique spin dynamics of the atomic ensemble in the SERF regime. A single channel sensitivity of 8 f·THz −1/2 is achieved with our SERF magnetometer.
The light-pumped atomic magnetometer is one of the most important high sensitivity magnetometers, [ 1 – 5 ] it has a sensitivity orders of magnitude better than the fluxgate magnetometer and magnetometers based on the Hall effect [ 6 ] and the magnet GMR [ 7 ] effect. Besides the advantage of sensitivity, the atomic magnetometer does not require cryogenic cooling as the superconducting quantum interference device (SQUID) magnetometer, and offers great potential for miniaturization. [ 8 ]
In the last decade, the spin-exchange relaxation free (SERF) atomic magnetometer [ 9 , 10 ] has significantly improved the sensitivity of the atomic magnetometers. With the reported sensitivity of 0.16 f·THz −1/2 [ 11 ] and the projected fundamental limits below 2 a·THz −1/2 , [ 12 ] the sensitivity of the SERF magnetometer rivals and even surpasses that of the best low temperature SQUID magnetometer. [ 13 ] In recent years, significant progress has been witnessed in the development of the SERF magnetometer. [ 14 , 16 – 20 ] As a result, the SERF magnetometer has found many important applications where ultra high sensitive magnetic field measurements are required. For example, the precision measurement of the electron electric dipole moments (EDM) can provide critical constraints of parameters for theories beyond the standard model, [ 21 ] the investigation of the tiny magnetization field in ancient rocks is very important for the paleomagnetism research, [ 11 ] and the geomagnetic anomalies measurement is a powerful tool in mining and the anti-submarine warfare. [ 22 ] Furthermore, the SERF magnetometer is well suited for biomagnetic measurements, there are already successful applications of the SERF magnetometer in magnetoencephalography (MEG) [ 23 ] and magnetocardiography (MCG). [ 24 ]
In this paper, we present our experimental results of the potassium SERF magnetometer. We will first discuss the SERF mechanism, then we will describe the details of our experimental setup. Because it is very important to identify the SERF and non-SERF regimes, we will next present a pump– probe experiment for this purpose. Finally, we will show our magnetometer signal and the noise spectrum, which indicate a single channel sensitivity of 8 f·THz −1/2 .
The sensitivity of the atomic magnetometer is limited by the coherence time of the atomic ensemble, and one of the most important decoherence mechanisms is the spin-exchange collisions. The spin-exchange collisions are the collisions between the alkali atoms which conserve the total spin of the colliding atoms but flip the electron spin of each of the atoms. The spin-exchange collisions lead to random transfers between the two ground state hyperfine levels of the atoms, which have the opposite directions of Larmor precession. When the atoms precess in different directions and at different angular speeds with each other, the total spin of the atomic ensemble become smaller, which leads to the spin relaxation of the atomic ensemble.
Demonstrated by Happer et al ., [ 25 , 26 ] the effects of the spin-exchange relaxation can be suppressed in the SERF regime, when the spin-exchange rate is much larger than the Larmor precession frequency. In the SERF regime, the atoms go through many spin-exchange collisions during one cycle of Larmor precession, being quickly switched between different ground states, each atom will go through the same average precession rate, so they remain synchronized in the precession process and do not suffer from the decoherence any more.
The experimental setup of the potassium SERF magnetometer is shown in Fig. Experimental implementation of the K magnetometer. Transverse polarization is detected using optical rotation.
We use a five-layer μ-metal magnetic shield with an expected shielding factor of 10 9 to isolate the system from the ambient magnetic field. The geometry of the shield is optimized with both theoretical calculations and finite element numerical simulations. The diameters of the inner and outer shields are 16 cm and 35 cm, the lengths of the inner and outer shields are 53 cm and 73 cm, respectively. A set of coils inside the shields allows the control of the magnetic field in the x , y , and z directions. The potassium atoms are optically pumped by a circularly polarized light tuned to the D1 line from a diode laser (Toptica DL100). A linearly polarized light from a diode laser (Toptica DLpro) 68 GHz red detuned from the D2 line is used to probe the polarization of the atoms. Both pump and probe lasers are Gaussian beams with diameter (full width at half maximum) of 4 mm.
The atoms are polarized by the optical pumping beam along the z direction, their transverse polarization P x caused by the magnetic field along the y direction is measured from the optical rotation angle of the linear polarized probe beam propagating along the x direction.
From the Bloch equation, [ 12 , 27 – 29 ] the optical rotation angle of the linearly polarized probe light is a dispersive function in the regime near zero magnetic field
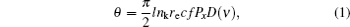
In the experiment, we slowly scan B y from −7 nT to 7 nT, the polarization rotation angle of the probe light is shown in Fig. Polarization rotation angle of the probe beam as a function of B y , showing a dispersive line shape with a line width of 1.7 nT and a zero crossing slope of 7 mrad/nT.
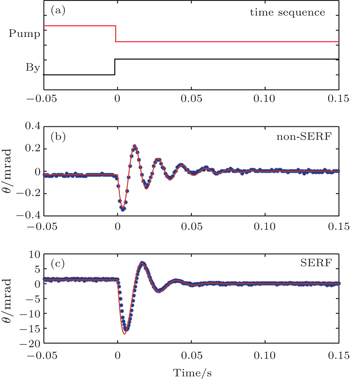
It is very important to clarify whether the magnetometer is running in the SERF regime or not in the experiment. Usually, people can find some evidence from the signal of the magnetometer such as those shown in Fig.
In this paper, we use a pump–probe approach to study the spin dynamics in the magnetometer. By observing the time-dependent damped precession signal, we can find direct evidence for whether the magnetometer works in the SERF regime or not. The time sequence of the experiment is shown in Fig.
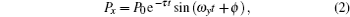
The difference of the spin precession rate in the SERF and non-SERF regimes gives the best evidence of SERF regime in the experiment, because the precession rate is only related to the nuclear spin of the atoms which is precisely known, and the external magnetic field which can be easily measured. The experiment can also be done in the SERF and non-SERF regimes under the same external magnetic field by changing only the temperature of the vapor cell, the ratio of the precession rate is thus not related to the magnetic field, making the result even clearer.
In our experiment, we measure the spin precession rate at the temperatures of 85 °C (Fig.
From the fit, in the presence of 9 nT magnetic field, the precession frequency is 63 Hz at 85 °C, which is in good agreement with the Larmor precess frequency of free atoms, but at 150 °C, the precession frequency is 42 Hz, which is clearly slower than the former and in good agreement with the prediction from the SERF theory (Eq. (
In order to calibrate the sensitivity of the SERF magnetometer, a sinusoidal calibration field of B rms = 120 pT at 20 Hz is applied, the sensitivity data are obtained by recording the output of the magnetometer for 100 s, performing a fast Fourier transform (FFT) without windowing, and calculating the r.m.s. amplitudes in 1 Hz bins, [ 9 ] as shown in Fig. Noise spectrum of the magnetometer signal with B y = 120 pT applied at 20 Hz, giving a sensitivity of 8 f·THz −1/2 .
Apart from several peaks from technical noise, the magnetic sensitivity is 8 f·THz −1/2 at 20 Hz. Further improvement of the sensitivity can be achieved by improving the performance of the magnetic shield and reducing the noise from the electronics and optical system.
In summary, we have successfully set up a potassium atomic SERF magnetometer and achieved a magnetometer sensitivity of 8 f·THz −1/2 . A pump and probe experiment is conducted to measure the spin precession frequency and relaxation time, which clearly prove that our magnetometer is working in the SERF regime. The sensitivity of our magnetometer ranks among the best in the world, further research and application of the SERF magnetometer will be possible in the near future.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 |