Cite this Article
Wang Wen-Bo, Zhang Xiao-Dong, Chang Yuchan, Wang Xiang-Li, Wang Zhao, Chen Xi, Zheng Lei. Denoising of chaotic signal using independent component analysis and empirical mode decomposition with circulate translating. Chinese Physics B , 2016, 25(1): 010202  
Permissions
Denoising of chaotic signal using independent component analysis and empirical mode decomposition with circulate translating
Wang Wen-Bo 1, 2, †, , Zhang Xiao-Dong 2 , Chang Yuchan 3 , Wang Xiang-Li 4 , Wang Zhao 5 , Chen Xi 5 , Zheng Lei 6
College of Science, Wuhan University of Science and Technology, Wuhan 430065, China
State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, China
School of Finance, Renmin University of China, Beijing 100872, China
School of Computer Science and Technology, Wuhan University of Technology, Wuhan 430063, China
College of Information Science and Engineering, Wuhan University of Science and Technology, Wuhan 430081, China
Wuhan NARI Limited Liability Company of Sate Grid Electric Power Research Institute, Wuhan 430074, China

 

Project supported by the National Science and Technology, China (Grant No. 2012BAJ15B04), the National Natural Science Foundation of China (Grant Nos. 41071270 and 61473213), the Natural Science Foundation of Hubei Province, China (Grant No. 2015CFB424), the State Key Laboratory Foundation of Satellite Ocean Environment Dynamics, China (Grant No. SOED1405), the Hubei Provincial Key Laboratory Foundation of Metallurgical Industry Process System Science, China (Grant No. Z201303), and the Hubei Key Laboratory Foundation of Transportation Internet of Things, Wuhan University of Technology, China (Grant No.2015III015-B02).

Abstract
Abstract

In this paper, a new method to reduce noises within chaotic signals based on ICA (independent component analysis) and EMD (empirical mode decomposition) is proposed. The basic idea is decomposing chaotic signals and constructing multidimensional input vectors, firstly, on the base of EMD and its translation invariance. Secondly, it makes the independent component analysis on the input vectors, which means that a self adapting denoising is carried out for the intrinsic mode functions (IMFs) of chaotic signals. Finally, all IMFs compose the new denoised chaotic signal. Experiments on the Lorenz chaotic signal composed of different Gaussian noises and the monthly observed chaotic sequence on sunspots were put into practice. The results proved that the method proposed in this paper is effective in denoising of chaotic signals. Moreover, it can correct the center point in the phase space effectively, which makes it approach the real track of the chaotic attractor.

PACS : 02.30.Nw ; 31.70.Hq
Keyword : independent component analysis ; empirical mode decomposition ; chaotic signal ; denoising
1. Introduction

With the influence of the measuring accuracy and the external environment, the actual measured chaotic signals are inevitably mixed with noises. Thus, the real dynamic behaviors of chaotic signals are concealed, which influence the parameter calculation and the precision of prediction. [ 1 ] How to reconstruct the chaotic signals from noises and how to achieve the real attractor structure utilizing the geometry characteristic of the manifold of the original chaotic attractor have been urgent problems to be resolved. [ 2 – 4 ] However, chaotic signals are actually broadband and their frequency bands are always partly overlapped with that of other signals, so it is difficult to separate the signals using traditional methods such as frequency spectrum analysis and linear filtering, and new methods are needed to distinguish the chaotic signal from other signals.

So far, some methods of noise reduction have been proposed. The structural cost function method and statistical model method, both of which are based on the existing chaotic dynamic characteristics, denoise the signal by comparison and prediction of the tract of attractors. These two methods are limited to chaotic time series whose dynamic features are known. [ 5 , 6 ] The local average method [ 7 ] denoises the signal by local linear approximation without a priori knowledge of chaotic dynamics. However, this method is too simple to describe the nonlinear dynamic characteristics of chaotic time series. In addition, there is another method called the local projection method [ 8 ] which was narrowly used because of its large and difficult calculation. Besides these, the compressed sensing perspective denoising method [ 10 ] is based on the deterministic projection matrix, and the parameter optimization nonlinear denoising method [ 11 ] is based on adaptively selecting the optimal window length.

The denoising of chaotic signal based on the wavelet transform can produce a good result, [ 12 , 13 ] it can analyze the local characteristics of signals in the time–frequency field with a simple calculation. However, the wavelet base and the number of the decomposition level, which play an important role in the result according to the research, [ 14 , 15 ] must be fixed before denoising. Hence, the wavelet transform is limited to denoising the signal. A new method, called empirical mode decomposition (EMD) [ 16 ] and proposed by Huang, is better than the wavelet transform and is a data driven and self-adapting denoising method. EMD can decompose the original signal into a group of physical meaningful intrinsic mode functions (IMFs). The most competitive advantage of EMD over wavelet transform is that the base function and the number of decomposition level in EMD need not to be given and the algorithm itself can get these parameters according to the characteristics of signals.

The signal denoising algorithm based on EMD has been widely researched. Boudraa proposed an algorithm [ 17 ] based on partial reconstruction of EMD. It eliminates some high frequency IMFs and accumulates the rests. This method loses lots of details while cannot reduce the noise totally. Olufemi developed the partial reconstruction method into a new one known as the EMD threshold denoising method. [ 18 ] However, this method does not consider the intrinsic characteristics of EMD and destroys the integrity of module unit. By contrast, the method of threshold denoising based on module unit does not destroy the integrity of the module unit. [ 19 ] It makes further improvement in the denoising but detail-keeping ability. This method is still limited in the usage mainly because of the difficulty in defining the threshold of module unit.

Zhang et al. [ 20 ] studied the variance characteristics of the chaotic signal in different conditions and proposed an adaptive denoising algorithm on account of EMD decomposition layers. The algorithm can adaptively select the IMF layer which needs to be processed, based on the relation between the maximum variance corresponding layer and the total number of decomposition of EMD, then removes the noise of the selected IMFs by the lifting wavelet. Wang et al. [ 21 ] proposed an adaptive chaotic signal denoising method based on the noise-assisted nonuniformly sampled bivariate empirical mode decomposition. The method estimates the noise energy of each IMF in the real part according to the energy of each IMF in the imaginary part, and removes the noise of each IMF in the real part by using the singular value decomposition. However, due to that the theory of EMD is not a complete system, it is very difficult to accurately estimate the distribution mode of noise coefficients and the energy of noise in each IMF, which limits the applications of the proposed methods in Refs. [ 20 ] and [ 21 ].

Therefore, the way to denoise IMFs based on their statistical property is the way to optimize the denoising results. The independent component analysis (ICA) proposed in the research of blind signal separation is known as a self-adaptive optimal algorithm [ 22 ] and works on the base of higher statistical characteristics. It regains the original signal from the composite signal according to the statistical characteristics of the original signal when their parameters are unknown. The ICA is now widely concerned in the area of redundancy reduction and denoising. [ 23 ] It is able to separate the desired signal from noises with the original independent signal components integrated in both time and frequency domains just under the condition that the observational signal is the summation of the independent desired signal and noises. Consequently, the ICA is quite appropriate for the IMF denoising. [ 24 ] In this article, we proposed a denoising algorithm combining ICA with EMD. It decomposes the original signal into IMFs using EMD and constructs the multi-dimensional input vectors of each IMF by circulate translating firstly, and denoises the IMFs with ICA secondly, then composes the denoised IMFs. According to the experiment, this algorithm can denoise the chaotic signal effectively while the midpoint position in the phase space can be exactly corrected.

2. Independent component analysis theory

Independent component analysis (ICA) is a new method for signal processing, which has been used widely recently in many aspects including signal filtering. [ 22 , 23 ] The basic ideal of ICA is to obtain the independent approximate value of the original signal by estimating it utilizing its higher statistical characteristics. 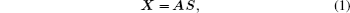Suppose that x 1 , x 2 , …, x m are M random observational vectors which are combined linearly by N unknown independent components, namely, s 1 , s 2 , …, s N . The mathematical model of ICA can be expressed as

where X = [ x 1 , x 2 , …, x M ] T , S = [ s 1 , s 2 , …, s N ] T , A is an M × N mixed matrix, and A and S are unknown. What ICA can solve is to estimate A and S with x i and prior knowledge of S . Generally, we assume that: (i) original signals needed to be estimated are independent statistically; (ii) no more than one original signal obeys the Gaussian distribution. In fact, ICA is used to construct a disjunctive matrix W so as to make y i that is a component of M -dimensional output vector Y = W X be mutual independent. Thus, an estimate of the original signal s i will be obtained as ŝ i = y i .

In the application of ICA, the observational data are needed to be pretreated. The pretreatment can reduce the computational complexity, and enhance the stability of the algorithm. The centralization and decorrelation are the most basic pretreatments of ICA,

The Fast ICA and Infomax are two most usually used algorithms in ICA. [ 23 , 24 ] Taking into account the problem of calculating speed, the Fast ICA algorithm is used in this paper. The Fast ICA algorithm, based on the principle of non-Gaussian maximization of negative entropy or kurtosis, finds non-Gaussian maximization of W X with fixed-point iteration theory. This method separates one independent component every time from observational signal using Newton iterative algorithm. Due to that kurtosis is sensitive to data, the negative entropy is used in this paper to realize non-Gaussian maximization of mixed signal. For an extraneous variable, the approximate negative entropy is defined as [ 22 ]

where y is the observation signal processed by the center and decorrelation, v is a Gaussian variable with zero-mean and unit variance, and G is a non-quadratic function. The FastICA is as follows.

3. Denoising of chaotic signal based on ICA and EMD
3.1. The empirical mode decomposition of chaotic signal

Empirical mode decomposition (EMD) aims at decomposing the origin signal into a series of intrinsic mode functions (IMF) with time scale feature. The IMFs must obey the following two conditions: one is that the difference between the number of IMFs’ extreme points and the number of its zero points is no more than 1; another is that the envelope line made up by maximum value points and minimum value points has a zero mean. [ 16 ] After decomposed by EMD, the chaotic signal x ( t ) can be expressed by a series of IMFs and a remainder term. That is

where imf i is the i -th IMF component and r L ( t ) is the remainder term. If x ( t ) is polluted by additive noises, the noise in imf i obeys the additive noise model approximately, [ 25 ] namely,

where y i is the unpolluted signal, n i is noises, y i and n i are independent of each other.

3.2. Construction of multi-dimensional input vector in denoising of IMF by ICA

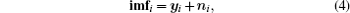
After the process of EMD, the chaotic signal will be decomposed into a series of IMFs which have different frequencies. Each IMF is a mono-component with a single form. After the noisy chaotic signal is decomposed by EMD, the noise will distribute in every IMF. If the IMFs can be effectively filtered, the noise will be eliminated either. The composition of the filtered IMFs is just the denoised chaotic signal. In this paper, ICA is used to filter each IMF. To ensure ICA can work normally, the number of signals must be larger than the number of independent sources, that is, the input vectors must be multi-dimensional. However, the decomposed signal has only one IMF in every frequency layer. Li et al. [ 24 ] have solved this problem by constructing virtual noise channels. They chose some IMFs as pure noises from all IMFs by Hilbert spectrum. Actually, this method is equal to EMD denoising of partial composed in essential, and its result is not very well.

In practice, the first layer of IMFs is almost made up of noise. We raise a new constructing method of multi-dimensional input vectors by the idea of translation invariable EMD. [ 19 ] After decomposing of EMD, the different noise samples will be obtained by the cyclic shift of the first IMF. Superimposing the noise samples with the remainder IMFs, and a group of noisy signals which have the same signal to noise ratio will be made. The new obtained noisy signals have almost unchanged desired signals and almost unchanged noise power. Thus, when EMD is carried out in the new obtained signals, the same layer IMFs almost have the same basic information, only the forms of noise are different. So the group of IMFs by translation invariable EMD can be used to construct multi-dimensional input vectors. The circulate translating of the first IMF( imf 1 ) is defined as follows.

The concrete steps of constructing multi-dimensional input vectors of ICA can be described as follows.

Step 1 Decomposing chaotic signal x ( t ) by EMD, we can obtain L IMFs. Denote them by imf 1 , imf 2 , …, imf L , then mark

Step 2 By cyclic shifting the first IMF for P times, P shifted data can be obtained as

Step 3 Construct new noisy signal

Step 4 Decompose x α ( t ) ( α = 1,2, …, P ) into L IMFs, namely

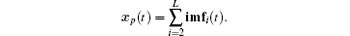
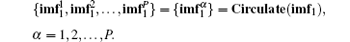
In the proposed method, we take 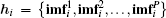imf i and as the input vectors when denoising the imf i . By now, the input vector has been constructed, and ICA can be carried out to denoise every layer of IMFs.

3.3. Denoising of chaotic signal based on ICA and EMD

After the denoising of IMFs based on ICA is done, the denoised chaotic signal will be obtained by composing all denoised IMFs and the remainder term. The denoising can be described as follows.

Step 1 Signal decomposing. The noisy chaotic signal with EMD and L layers IMF { imf i }, i = 1,2, …, L in different scales can be obtained.

Step 2 Constructing input vectors. In this step, a vector collection h i , i = 1,2, …, L is constructed by the method introduced in Section 3.2.

Step 3 Denoise IMFs using ICA. In this step, choose { imf i , h i − imf i } as the ( P + 1)-dimensional inputting vectors, and denoise imf i by ICA, where set P = 100. Assume that is the denoised value.

Step 4 IMFs composing. By adding and remainder term r L , the denoised chaotic signal x ( d ) ( t ) is received. That is

4. Experiment analysis of chaotic signal denoising

In order to verify the validity of the method proposed in this paper, a Lorenz chaotic signal composed of different Gaussian noises and the monthly observational chaotic sequence on sunspots have been researched. For a comparison, the EMD threshold denoising method based on coefficient [ 18 ] and the EMD threshold denoising method based on module unit [ 19 ] have also been used to remove noises for chaotic signals. In this paper, the effect of noise reduction is evaluated in two ways.

4.1. Chaotic signal denoising of Lorenz system

The dynamic equation of Lorenz system is

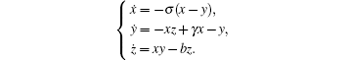
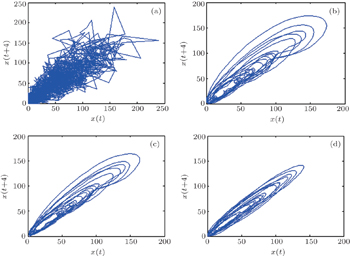
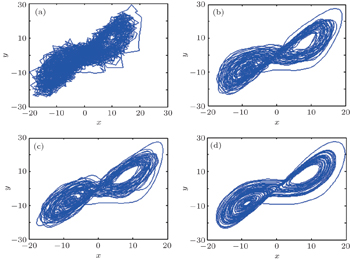Let σ = 10, γ = 28, and b = 8/3, then this system is chaotic. This system is numerically simulated in Matlab by four-order Runge–Kutta method. The step length was set to be 0.01, and the initial value was y (1,1) = 15, y (1,2) = 2, y (1,3) = 0. To simulate the chaotic signal, 50000 points were generated as shown in Fig.  1(a) . Firstly, three methods mentioned above were respectively used to denoise noisy Lorenz signal with 65% noise intensity. The denoised time series signal and its 2-dimensional and 3-dimensional phase graphs are shown in Figs.  2 and 3 , respectively. SNR and RMSE of the denoised signal are shown in Table  1 .

Fig. 1. The 2-dimensional phase graph of noisy and denoised Lorenz signal: (a) 65% noisy signal; (b) EMD threshold denoising; (c) EMD mode threshold denoising; (d) EMD-ICA denoising.
Fig. 2. The 3-dimensional phase graph of noisy and denoised Lorenz signal: (a) 65% noisy signal; (b) EMD threshold denoising; (c) EMD mode threshold denoising; (d) EMD-ICA denoising.
Fig. 3. The 2-dimensional phase graph of noisy and denoised monthly sunspot signal: (a) observed signal; (b) 2-dimensional phase graph after EMD threshold denoising; (c) 2-dimensional phase graph after EMD mode threshold denoising; (d) 2-dimensional phase graph after EMD-ICA denoising.
Table 1.

SNR (dB) and RMSE of denoisied chaotic signals.

.

By comparing Figs.  1(b) – 1(d) and Figs.  2(b) – 2(d) , respectively, the signal denoised by the method proposed in this paper is more similar to the origin signal (shown in Fig.  1(a) ). That is to say, EMD-ICA denoising method can show the geometric structure of original signal’s chaotic attractors more clearly. As is shown in Table  1 , EMD-ICA method has the maximum SNR and the minimum RMSE. In order to further compare the experimental results, those three methods have also been implemented respectively in these noisy Lorenz chaotic signals with 25%, 45%, 85% noise intensity. The results shown in Table  1 give evidence to the experiment. In conclusion, for a model known chaotic system, EMD-ICA method can eliminate noises more effectively.

4.2. Denoising of monthly sunspot signal

Recently, with the development of the theory of chaos, the research on chaotic characteristics of sunspot is increasing. During the observation, the observed data are always mixed with noises, so denoising must be executed to origin data. In our experiment, sunspot data observed from Jan. 1749 to Mar. 2007 are chosen, and three methods mentioned above are used to denoise the sunspot signal. The phase graphs of original data and denoised data are shown in Fig.  3 .

As shown in Fig.  3 , the noisy signal has a rambling pseudorandom characteristic while the denoised signal has a clear and regular geometric structure of chaotic attractors. The intrinsic certainty of the denoised chaotic signal is increased, and the dynamic characteristics of the chaotic system are appeared. The smooth and regular structure indicates the validity of this method proposed in this paper. SNR and RMSE of denoised sunspot signal are listed in Table  1 . EMD-ICA denoising method has the maximum SNR and the minimum RMSE. In conclusion, for real signals, EMD-ICA is also the most effective method among these three methods.

4.3. Analysis of experimental results

In experiments, the denoising algorithm of EMD coefficient threshold separates all IMFs into high frequency and low frequency groups by mutual information firstly; secondly, a denoising procedure is applied only to the high frequency groups using the Stein’s unbiased risk estimate threshold; thirdly, the denoisied high frequency IMFs are combined with the low frequency group to obtain the overall denoisied signal. The denoising algorithm of EMD mode threshold uses the mode cell as the basic unit, and calculates the mode threshold by the noise distribution model, the noise variance, and the noise energy in each IMF. Then, if the maximum of a mode cell is lower than the mode threshold, this mode cell will be set to zero, and if the maximum of a mode cell is greater than the mode threshold, this mode cell will maintain.

Obviously, the denoising algorithms of EMD coefficient threshold and EMD mode threshold need the energy density, distribution model, variance, etc., of the noise in each IMF. However, the EMD is based on experiment, and its theory is not complete. Therefore, the distribution mode, energy intensity, and variance of the noise in IMF only are estimated by experience, but cannot be deduced and analyzed by theory, which leads to that the obtaining values are not universal. Therefore, in the denoising algorithms of EMD coefficient threshold and EMD mode threshold, the method of calculating the statistical characteristics of noise in IMF is not necessarily suitable for the denoising of chaotic signal. Directly applying the two algorithms to denoising chaotic signal, the denoising effect will inevitably be affected seriously.

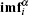
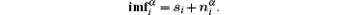
The proposed method in this paper, firstly decomposes the chaotic signal with the noise by EMD, then constructs the input vectors By supposing imf i = s i + n i , where s i is the useful signal and n i is the noise, as known from the construct principle of circulate translation, the useful signal contained is almost the same as the useful signal of imf i , only the noise distributions are different. Therefore, we can suppose

Set according to the characteristic of circulate translation, n i noise can be composed linearly by By supposing and then the input vector can be marked as

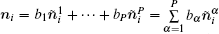
According to the property of ICA, the useful signal of 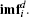imf i can be recovered and imf i is adaptively denoisied by ICA. Then, the denoisied chaotic signal is obtained by accumulating all denoisied IMF The proposed method based on ICA and EMD does not use the statistical properties of the noise in each IMF, and only uses the properties of IMF’s own coefficient to adaptively remove the noise of IMF.

ICA works on the base of higher statistical characteristics. It can recover the original signals from the composite signal only according to the original signal’s basic statistical characteristics even if the parameters of original are unknown. Therefore, when using ICA to remove the noise of IMFs of the noisy chaotic signal, the statistical characteristics of noise in each IMF are not needed, we only need to suppose that IMF is linearly superposed by the useful signal and noise. The denoisied IMF by using ICA is integrated both in time and frequency domains, so the ICA is very suitable for the denoising IMF of the chaotic signal. In this paper, we make full use of the characteristics of EMD decomposition and ICA denoising to reduce the noise of the chaotic signal. The proposed method can remove the noise of each IMF as much as possible, and more effectively keep the useful signal details.

5. Conclusions

In order to further improve the noise reduction effect of EMD on the chaotic signal, in this paper, a new chaotic signal denoising method of combining ICA and EMD is proposed. This method eliminates the noises effectively and maintains useful information better by denoising IMFs with ICA. The experiments are carried out on the Lorenz signals and the monthly sunspot signals. The experiment results show that the method proposed in this paper is more effective in denoising of chaotic signal in comparison with the existing EMD denoising methods. The de-noised signals show clearer geometric structures of chaotic attractors. The EMD is an iterative decomposing algorithm with large computation cost, so the efficiency of the proposed method is not high. How to use an appropriate parallel algorithm to improve the computing efficiency is the key point in the future.

Reference
1 Li G L Chen X Y 2008 Acta Electron. Sin. 36 1814 (in Chinese)
2 Vicha T Dohnal M 2008 Chaos Solitons Fractals 38 70
3 Xie Z B Feng J C 2010 Chin. Phys. B 19 050510
4 Lu S X Wang Z S Hu Z H Feng J C 2014 Chin. Phys. B 23 010506
5 Dedieu H Kisel A 1999 Int. J. Circuit Theory Appl. 27 577
6 Jako Z Kis G 2000 IEEE Trans. Circuits Syst.-I: Fundamental Theory and Applications 47 1720
7 Schreiber T 1993 Phys. Rev. E 47 2401
8 Han M Liu Y H Shi Z W Xiang M 2007 Journal of System Simulation 19 364 (in Chinese)
9 Leontitsis A Bountis T Pagge J 2004 Chaos 14 106
10 Li G M Lu S X 2015 Acta Phys. Sin. 64 160502 (in Chinese)
11 Wang M J Wu Z T Feng J C 2015 Acta Phys. Sin. 64 040503 (in Chinese)
12 Murguia J S Canton C E 2006 Revista Mexicana De Fisica 52 155
13 Liu Y X Yang G S Jia Q 2011 Acta Electron. Sin. 39 13 (in Chinese)
14 Zhang L Bao P Wu X 2005 IEEE Transactions on Circuits and Systems for Video Technology 15 469
15 Zhang H Chen X H Yang H Y 2011 Oil Geophysical Prospecting 46 70
16 Huang N E Shen Z Long S R 1998 Proc. R. Soc. Lond. A 454 903
17 Boudraa A Cexus J 2007 IEEE Trans. on Instrumentation and Measurement 56 2196
18 Olufemi A Vladimir A Auroop R 2011 IEEE Sensors Journal 11 2565
19 Kopsinis Y Mclaughli S 2009 IEEE Trans. Signal Process. 57 1351
20 Zhang Q Xing H Y 2015 Acta Electron. Sin. 43 901 (in Chinese)
21 Wang X F Qu J L Gao F Zhou Y P Zhang X Y 2014 Acta Phys. Sin. 63 170203 (in Chinese)
22 Hyvarinen A Oja E 2000 Neural Networks 13 411
23 Zhang Z S Yu J Yan Q Meng Y S Zhao Z 2011 Acta Geodaetica et Cartographica Sinica 40 289
24 Li H Sun Y L 2007 Journal of Beijing University of Posts and Telecommunications 30 33
25 Zhao H W Norden E H 2004 Proc. R. Soc. Lond. A 460 1597