Cite this Article
Wei Han-yu, Xia Tie-cheng. A new six-component super soliton hierarchy and its self-consistent sources and conservation laws. Chinese Physics B , 2016, 25(1): 010201  
Permissions
A new six-component super soliton hierarchy and its self-consistent sources and conservation laws
Wei Han-yu 1, †, , Xia Tie-cheng 2
College of Mathematics and Statistics, Zhoukou Normal University, Zhoukou 466001, China
Department of Mathematics, Shanghai University, Shanghai 200444, China

 

Project supported by the National Natural Science Foundation of China (Grant Nos. 11547175, 11271008 and 61072147), the First-class Discipline of University in Shanghai, China, and the Science and Technology Department of Henan Province, China (Grant No. 152300410230).

Abstract
Abstract

A new six-component super soliton hierarchy is obtained based on matrix Lie super algebras. Super trace identity is used to furnish the super Hamiltonian structures for the resulting nonlinear super integrable hierarchy. After that, the self-consistent sources of the new six-component super soliton hierarchy are presented. Furthermore, we establish the infinitely many conservation laws for the integrable super soliton hierarchy.

PACS : 02.30.Ik ; 02.30.Jr ; 02.20.Sv
Keyword : super Hamiltonian structures ; self-consistent sources ; conservation laws ; Fermi variable
1. Introduction

In recent years, with the development of integrable systems, super integrable systems have attracted a great deal of attention. Since 1986, Chowdhury and Roy have already considered the super trace identity. [ 1 ] Hu presented the super trace identity in 1997, but he did not give its rigorous proof. [ 2 ] Later, Ma gave a systematic proof of the super trace identity and the expression of its constant γ . [ 3 ] For application, the super Hamiltonian structures of the super AKNS hierarchy and the super Dirac hierarchy have been obtained. Afterwards, super C-KdV hierarchy [ 4 ] and super Boussinesq hierarchy [ 5 ] as well as their super Hamiltonian structures are presented. The Bargmann symmetry constraint and binary nonlinearization of the super Dirac systems were given in Ref. [ 6 ].

Soliton equations with self-consistent sources have been paid considerable attention in recent years. The study on this topic has important physical applications. For example, the nonlinear Schrödinger equation with self-consistent sources is relevant to some problems of plasma physics and solid state physics. There are many methods to obtain exact solutions of soliton equations with self-consistent sources, such as the Darboux transformation method [ 7 ] and the inverse scattering transform method. [ 8 ] There are also some results to consider hierarchies with self-consistent sources. [ 9 , 10 ] Very recently, self-consistent sources for the super Broer–Kaup–Kupershmidt equation hierarchy was presented in Ref. [ 11 ].

The conservation laws play an important role in discussing the integrability for soliton hierarchy. An infinite number of conservation laws for the KdV equation was first discovered by Miura, Gardner, and Kruscal in 1968, [ 12 ] then lots of methods have been developed to find them. This may be mainly due to the contributions of Wadati et al. [ 13 ] Many papers dealing with symmetries and conservation laws were presented. The direct construction method of multipliers for the conservation laws was presented in Ref. [ 14 ].

In this paper, starting from a Lie super algebra, a 3 × 3 matrix super spectral problem is designed. With the help of variational identity, we get a new six-component super soliton hierarchy and its super Hamiltonian structures. In Section 4, the self-consistent sources of the new six-component super soliton hierarchy are obtained. In Section 5, we present the conservation laws for the new super soliton hierarchy.

2. A new six-component super soliton hierarchy

A soliton hierarchy is based on the spectral problem [ 15 ]

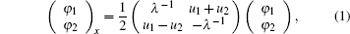
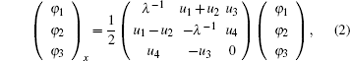
and a super extension of the soliton hierarchy can be constructed by the matrix super spectral [ 16 ]

where u 3 , u 4 , and φ 3 are fermion fields. It reduces to the system ( 1 ) as u 3 = u 4 = 0.

Based on the Lie super algebra G,

where e 1 , e 2 , e 3 are even and e 4 , e 5 are odd, that is along with the communicative operation

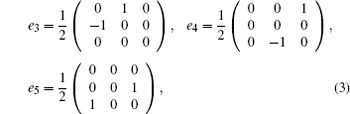
We will derive a generalized super soliton hierarchy. To this end, we take a 3 × 3 matrix super spectral problem

where

and , , , , , , , and . As u 3 , u 4 , u 5 , and u 6 are Fermi variables, they constitute Grassmann algebra.

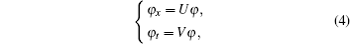
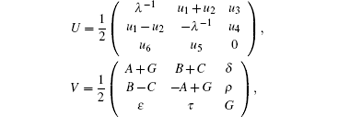
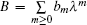
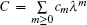
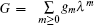
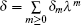
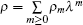
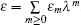
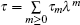
Starting from the stationary zero curvature equation

we have

Choose the initial data

From the recursion relations in Eqs. ( 5 ), the first few results can be obtained

Next, we consider the auxiliary spectral problem

where

Substituting Eq. ( 7 ) into the zero curvature equation

we obtain a new six-component super soliton hierarchy

When n = 2, the hierarchy ( 9 ) can be reduced to the second-order super nonlinear integrable couplings equations

By choosing u 3 = – u 5 and u 4 = u 6 , equations ( 10 ) can be reduced to the second-order super soliton equations [ 16 ]

3. Super Hamiltonian structures of the new six-component super soliton hierarchy

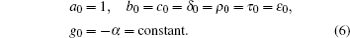
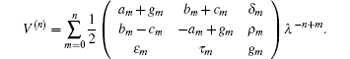
In this section, we will establish super Hamiltonian structures of the new six-component super soliton hierarchy by super trace identity [ 2 , 3 ]

where the constant γ is determined by

According to super trace identity on Lie super algebras, a direct calculation reads

Substituting the above formula into the super trace identity ( 12 ) yields

Comparing the coefficients of λ n +2 on both sides of Eq. ( 15 ) gives rise to

By employing the computing formula ( 13 ) on the constant γ , we obtain γ = 0. Therefore, we conclude that

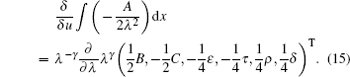
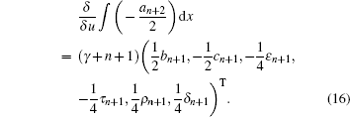
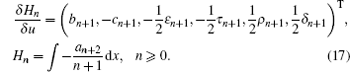
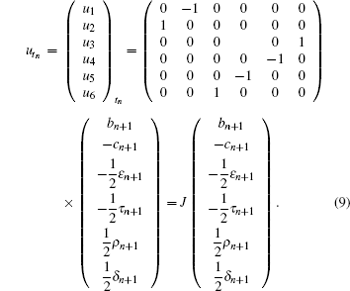
From the recursion relations in Eq. ( 5 ), we can obtain the hereditary recursion operator L which satisfies that

where

Therefore, the new super soliton hierarchy ( 9 ) possesses the following super Hamiltonian structures

4. Self-consistent sources of the new six-component super soliton hierarchy

Consider the linear system

Based on the result in Ref. [ 17 ], we can show that the following equation:

holds true, where α j are constants, determines a finite-dimensional invariant set for the flows

From Eq. ( 21 ), we may know that

where Str denotes the trace of a matrix and

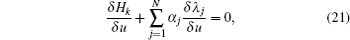
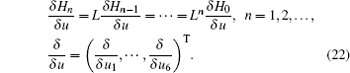
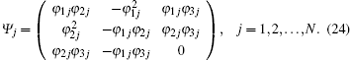
Based on Eq. ( 21 ), for system ( 9 ), we set

and obtain the following δ λ j / δu

where Φ i = ( φ i 1 ,…, φ iN ) T , i = 1,2,3.

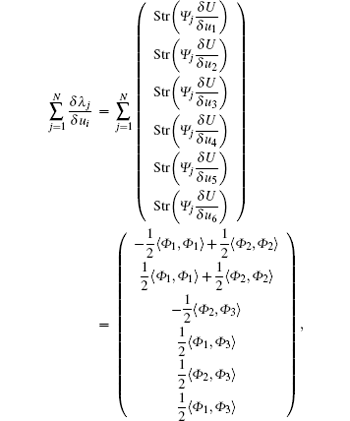
Therefore, the new six-component integrable super soliton hierarchy with self-consistent sources is proposed

For n = 2, we obtain the super soliton equation with self-consistent sources

where Φ i = ( φ i 1 ,…, φ iN ) T , i = 1,2,3 satisfy

5. Conservation laws of the new six-component super soliton hierarchy

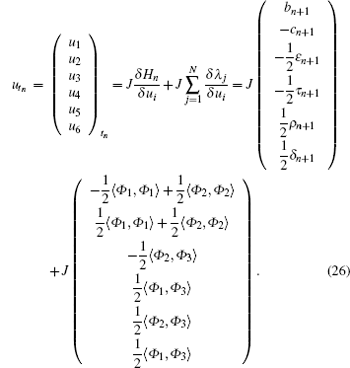
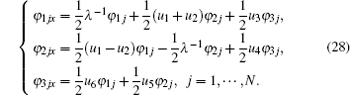
In the following, we will construct conservation laws of the new six-component super soliton hierarchy. We introduce the variables

From Eq. ( 4 ), we have

Expand E , K in the power of λ

Substituting Eqs. ( 31 ) into Eqs. ( 30 ) and comparing the coefficients of the same power of λ , we obtain

and a recursion formula for e j and k j

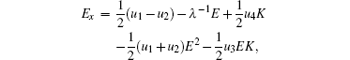
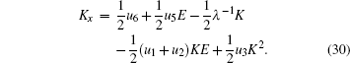
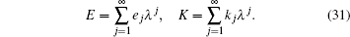
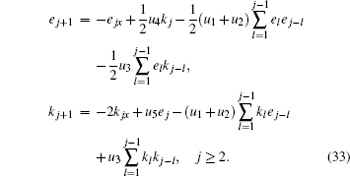
Because of

we assume that

Then equation ( 34 ) can be written as θ t = ν x , which is the right form of conservation laws. With regard to Eq. ( 10 ), we have

We expand θ and ν as a series in powers of λ with the coefficients

the first two conserved densities and currents of Eqs. ( 10 ) read

The recursion relations for θ j and ν j are

where e j and k j can be calculated from Eq. ( 33 ). We can display the first two conservation laws of Eq. ( 10 ) as

where θ 1 , ν 1 , θ 2 , and ν 2 are defined in Eq. ( 37 ). Then, the infinitely many conservation laws of Eq. ( 9 ) can be easily obtained from Eqs. ( 30 )–( 39 ), respectively.

6. Conclusions

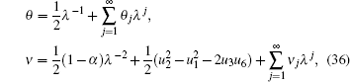
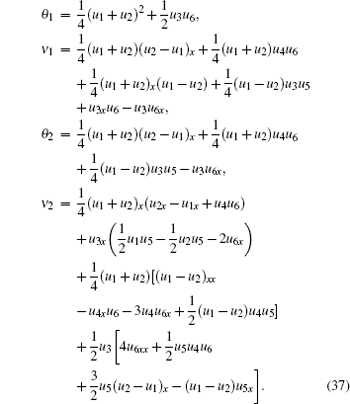
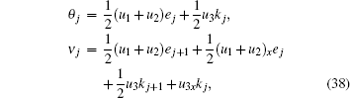
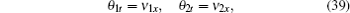
Starting from Lie super algebras, we obtain a new six-component super soliton hierarchy. With the help of variational identity, the Hamiltonian structures of the six-component super soliton hierarchy can be presented. Meanwhile, the super soliton hierarchy with self-consistent sources is established. Finally, we also derive the conservation laws of the six-component super soliton hierarchy. It is worth noting that the coupling terms of super integrable hierarchies involve Fermi variables, they satisfy the Grassmann algebra which is different from the ordinary one. Sometime we call super integrable system Eq. ( 9 ) as super Fermi extension. In fact, in Refs. [ 18 ]–[ 20 ], the authors gave many Lie algebras which have more complex mathematical structures, which deserves more meaningful work in the near future.

Reference
1 Chowdhury A R Roy S 1986 J. Math. Phys. 27 2464
2 Hu X B 1997 J. Phys. A: Math. Gen. 30 619
3 Ma W X He J S Qin Z Y 2008 J. Math. Phys. 49 033511
4 Tao S X Xia T C 2010 Chin. Phys. Lett. 4 040202
5 Tao S X Xia T C 2010 Chin. Phys. B. 7 070202
6 Yu J He J S Ma W X Cheng Y 2010 Chin. Ann. Math. Ser. B 31 361
7 Zeng Y B 1994 Physica D 73 171
8 Meĺnikov V K 1992 Inverse Probl. 8 133
9 Yu F J Li L 2008 Chin. Phys. B 17 3965
10 Xia T C 2010 Chin. Phys. B 19 100303
11 Wei H Y Xia T C 2013 J. Appl. Math. 2013 913758
12 Miura R M Gardner C S Kruskal M D 1968 J. Math. Phys. 9 1204
13 Wadati M Sanuki H Konno K 1975 Prog. Theor. Phys. 53 419
14 Bluman G W Anco S C 2002 Symmetry and Integration Methods for Differential Equations New York Springer 419
15 Guo F K 1996 Math. Appl. 9 495
16 Li Z Dong H H Yang H W 2009 Int. J. Theor. Phys. 48 2172
17 Tu G Z 1990 Northeastern Math. J. 6 26
18 Zhang Y F 2011 Commun. Theor. Phys. 56 805
19 Zhang Y F Hou Y C 2011 Commun. Theor. Phys. 56 856
20 Zhang Y F Tam H Feng B L 2011 Chaos Soliton Fract. 44 968