†Corresponding author. E-mail: bangongxinxiang@126.com
*Project supported by the Youth Science Funds of Shandong Academy of Sciences, China (Grant No. 2014QN032).
Many real communication networks, such as oceanic monitoring network and land environment observation network, can be described as space stereo multi-layer structure, and the traffic in these networks is concurrent. Understanding how traffic dynamics depend on these real communication networks and finding an effective routing strategy that can fit the circumstance of traffic concurrency and enhance the network performance are necessary. In this light, we propose a traffic model for space stereo multi-layer complex network and introduce two kinds of global forward-predicting dynamic routing strategies, global forward-predicting hybrid minimum queue (HMQ) routing strategy and global forward-predicting hybrid minimum degree and queue (HMDQ) routing strategy, for traffic concurrency space stereo multi-layer scale-free networks. By applying forward-predicting strategy, the proposed routing strategies achieve better performances in traffic concurrency space stereo multi-layer scale-free networks. Compared with the efficient routing strategy and global dynamic routing strategy, HMDQ and HMQ routing strategies can optimize the traffic distribution, alleviate the number of congested packets effectively and reach much higher network capacity.
A wide range of communication systems can be represented as complex networks, [1– 8] in which the elementary components are nodes and each node exchanges information mutually by links.[9– 13] The network prototypes include data transmission in the Internet, land environment observation network, oceanic monitoring network, [14] and so on. Since the discovery of some common features on real networks, such as small-world phenomena[15] and scale-free property, [16] the investigation on the traffic dynamic property of complex network has attracted growing interest from many engineering communities. It is widely proved that the topology and routing strategy of networks have profound effects on the transport processes of traffic flow.[17, 18]
In the past few years, the routing strategies and resource allocations for traffic dynamics of networks have been widely studied.[19– 27] In many realistic communication systems, developing a better routing strategy to enhance the network capacity is usually preferable to avoid high cost of changing infrastructure. Recently, the shortest path strategy is widely used in many systems. However, it neglects the effects of degree and betweenness of nodes and then it often leads to lower network capacity. For this purpose, some new routing strategies have been proposed for scale-free networks. Wang et al.[21] proposed a local structural information routing strategy where the packets are delivered based on the local information of neighbour nodes’ degree

It is proved that the maximal capacity corresponds to α = − 1 in the case of identical nodes’ delivering ability. Yan et al.[22] introduced an efficient routing strategy. In the efficient routing strategy, the packets are forwarded along the path where the sum degree between source node i and destination node j is a minimum. It is defined as

where k(xm) is the degree of node xm, and l is the path length. The highest network capacity is achieved when β is set to 1. The efficient routing can reach a very high network capacity, which is about ten times that of shortest path strategy. After that, Ling et al.[23] proposed a global dynamic routing strategy. In this strategy, the queue length of neighboring nodes is taken into consideration, and the packets are delivered along the path in which the sum queue length between source node i and destination node j is a minimum. It is denoted as

where q(xm) is the queue length of node xm. The network capacity with global dynamic routing strategy can be further improved to almost two times of that with the efficient routing strategy. However, in the real communication networks, the traffic is usually concurrent and many new created packets will choose the paths at the same time. Considering a circumstance where the global dynamic routing strategy is applied to find paths for many new created packets, synchronously, these new packets choose paths which meet the requirements of minimum queue length at the same time. However, the selected paths might travel through the same nodes that satisfy the condition of minimum queue length in the current time step, and in the next time step, lots of packets will be delivered to these nodes and these nodes will be hub nodes. Accordingly, the network congestion occurs, and the performances of global dynamic routing strategy descend. This phenomenon could also take place in efficient routing strategy.
At the same time, most of these investigations on traffic properties and controllability of traffic congestion are grounded on a basic assumption that the network topology structure is a single layer. Recently, Kurant et al.[28] and Zhuo et al.[29] introduced the layered network models that consist of a physical layer and a logical layer, and they investigated the traffic dynamics with the assumption that the logical and physical layers are relatively independent and isolated. However, in modern communication systems, many communication networks, such as oceanic monitoring network and land environment observation network, are space stereo multi-layer. Besides the information transmitted within each layer, the information exchange between layers also exists and all the layers are not independent and isolated. The network structure is space stereo multi-layer and all layers are connected by the traffic flow.
As the investigations for traffic dynamics are mainly based on the single layer or isolated layered networks and few attempts focus on the dynamic routing for traffic concurrency space stereo multi-layer scale-free network, therefore, it is of great interest to explore how this kind of topology affects the traffic dynamics, and the routing strategies that can achieve higher network capacity in traffic concurrency space stereo multi-layer scale-free network, such as oceanic monitoring network, is needed.
In this paper, we proposed a traffic model of space stereo multi-layer complex network and introduced two kinds of global forward-predicting dynamic routing strategies, global forward-predicting hybrid minimum queue (HMQ) routing strategy and global forward-predicting hybrid minimum degree and queue (HMDQ) routing strategy, for traffic concurrency space stereo multi-layer scale-free networks. Our discussions are interested in investigating the traffic dynamics in traffic concurrency scale-free network. Compared with the efficient routing strategy and global dynamic routing strategy, the proposed routing strategies can balance the traffic distribution, alleviate the number of congested packets effectively and achieve much higher network capacity for traffic concurrency space stereo multi-layer scale-free networks.
The paper is organized as follows. In the following section, we describe the traffic model of space stereo multi-layer network in Section 2 and the global forward predicting dynamic routing strategies in detail in Section 3. In Section 4, the simulation results of traffic dynamics are presented and discussed. In the last Section, the work is concluded.
Many real communication networks are space stereo multi-layer. Taking the oceanic monitoring network for example, the wireless sensors that construct the lower layer are randomly distributed on the interested sea area and then gathered the data of a certain monitoring area transmitting to the upper layer that consist of aircrafts or unmanned aerial vehicles. Accordingly, the traffic source and destination are distributed in the space stereo lower layer and upper layer respectively. Meanwhile, As the wireless sensor network is self-organized, the organization of traffic structure between layers or within one layer is usually hierarchical[30] so as to improve the network performances, such as network lifetime.
Similar to the structure of oceanic monitoring network and land environment observation network, the structure of our traffic model consists of an upper layer, a lower layer, and an inter-layer between them. The information gathered by the nodes in the lower layer is transmitted through the inter-layer to the nodes in the upper layer, that is to say, the source nodes located in the lower layer and the destination nodes distributed in the upper layer mainly focus on the information’ s collection and acquisition respectively. As the nodes in the lower layer and upper layer are only interested in the information within a certain range, the space stereo multi-layer network is divided into several districts. The traffic information from one district in lower layer is first delivered to the corresponding district in upper layer through one inter-layer between them and then gets to the destination according to the given routing strategy.
In order to improve the network performances, the nodes in the oceanic monitoring network or land environment observation network are usually organized as hierarchical structure, without loss of generality, this paper uses the well-known BA model to generate a hierarchical network. We construct the hierarchical network with BA model as follows: starting from v0 = 10 fully connected nodes and e0 = 6 links, a new node with one link is added to the existing network at each time step according to preferential attachment, i.e., the probability Π i that a link connects to the existing node i is proportional to its degree of ki
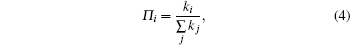
until the total number of nodes and average degree become N and 〈 k〉 , respectively.
 | Fig. 1. The illustration of space stereo-multi-layer network. (a) The traffic model structure of space stereo multi-layer network. (b) The packet transmission process. |
Figure 1 gives an illustration of space stereo multi-layer network. In the structure of traffic model of space stereo multi-layer network, the upper layer and lower layer are geographically divided into m × n square districts and each district can be represented as Φ mn (m ≥ 1, n ≥ 1) and Ψ m′ n′ (m′ ≥ 1, n′ ≥ 1), respectively. Nodes in district Ψ m′ n′ establish links to its corresponding nodes in district Φ mn (m = m′ , n = n′ ) and these links from each Ψ m′ n′ to Φ mn (m = m′ , n = n′ ) construct the traffic topology of inter-layer Ω mn. As the lower layer is made up of source nodes and these nodes mainly communicate to its corresponding nodes in the district of upper layer, we make the following assumptions in our model: (i) The nodes in the lower layer are distributed randomly. (ii) The traffic topology of inter-layer Ω mn is scale-free. (iii) The topology of upper layer is scale-free.
Figure 1(a) shows the traffic model structure of space stereo multi-layer network. The upper layer and lower layer are geographically parted into m × n districts and the inter-layer Ω mn is between them. The topology of inter-layer Ω mn is consisted of links from Ψ m′ n′ to Φ mn (m = m′ , n = n′ ). If one packet generated at node v1 in Ψ 1n′ , it will first travel through the inter-layer Ω 1n and select the next hop node v2 in the corresponding district Φ 1n. Subsequently, the packet will be forwarded along the route to its destination node v4. Thus, we can write the packet transmission process as
which is shown in Fig. 1(b).
The traffic model of space stereo multi-layer network is described as follows.
(i) At each time step, there are R packets generated and entered the system synchronously with randomly chosen source nodes in the lower layer and destination nodes in the upper layer.
(ii) Once a packet is generated at source node vi (1 ≤ i ≤ N) in Ψ m′ n′ , it will choose the next hop node vj (1 ≤ j ≤ N) in the corresponding district Φ mn, where m = m′ , n = n′ , and then, the packet will be transmitted to the destination node vk (1 ≤ k ≤ N) in the upper layer based on the given route strategy.
(iii) At each time step, one node in the network possesses the same ability on delivering most C packets to its next hop node. When a new packet is created at time t, it will be placed at the end of the node buffer, which contains the undelivered packets. During the following time steps t+ 1, t+ 2, … , t+ ℓ , the packet travels through ℓ nodes toward its destination.
(iv) The above process is repeated until the packet reaches its destination. Once a packet arrives at its destination, it is removed from the system.
In our model, the maximal queue length of each node is assumed to be unlimited. Each node can be treated as both host and router, [31] and each node possesses the same ability on handling packets. The first-in-fist-out discipline[32] is applied at each queue of node.
As we know, if paths are chosen synchronously in the traffic concurrency network without any prior knowledge of network’ s situation, the congestion will occur easily and the network capacity descends. To reduce the network congestion and optimize the traffic distribution for the traffic concurrency network, we introduce the traffic forward prediction scheme to the selection of paths and propose two dynamic routing strategies, global forward-predicting hybrid minimum queue (HMQ) routing strategy and global forward-predicting hybrid minimum degree and queue (HMDQ) routing strategy, which could further improve the system capacity.
In the global forward-predicting hybrid minimum queue routing strategy proposed for traffic concurrency network, the path selection is mainly grounded on two factors, one is the current node queue length, i.e., the number of packets in node buffer, and the other is the forward-predicting node queue length. That is, each node has two buffers, one is the current real buffer and the other is the virtual forward-predicting buffer. Once the path of one packet is selected, the nodes along this path are confirmed, and then, the forward-predicting node queue length of these nodes will be pre-marked and the virtual forward-predicting buffer length is added by one as the packet will be placed at their node buffer in the future. Consequently, the path selection for packets will take the current node queue length of current real buffer and the forward-predicting node queue length of virtual forward-predicting buffer into account, and find a minimum one for all possible paths. Moreover, when one packet is handled by node, the node queue length of both current real buffer and virtual forward-predicting buffer will be decreased by one. Therefore, the global forward-predicting hybrid minimum queue routing strategy can be denoted as
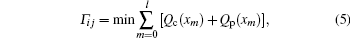
where Qc (xm) is the current queue length of node xm, Qp (xm) is the forward-predicting node queue length of node xm, and l is the path length.
Similarly, in the global forward-predicting hybrid minimum degree and queue routing strategy proposed for traffic concurrency network, the selected path is also mainly based on two factors, one is the node degree, and the other is the forward-predicting node queue length. Again, each node has also a virtual forward-predicting buffer. After the selection of a path for one packet, the queue length of these nodes along this route will be pre-marked and their virtual forward-predicting buffer length will be added by one. Accordingly, the path selection for packets will choose one that makes the sum of node degree and the forward-predicting node queue length of virtual forward-predicting buffer minimum. Therefore, the global forward-predicting hybrid minimum degree and queue routing strategy can be defined as
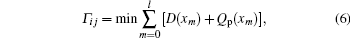
where D(xm) is the node degree of node xm, Qp (xm) is the forward-predicting node queue length of node xm, and l is the path length.
One of the most interesting characteristics of network is the ability of handling packets and delivering capacity. In order to describe the phase transition of traffic flow for introduced traffic model and routing strategies, we use the order parameter[33]
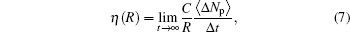
where Δ Np = Np (t+ Δ t)− Np (t), 〈 〉 indicates the average over time windows of width Δ t, and Np (t) is the total number of packets within the network at time t. The order parameter indicates the balance between the inflow and outflow. In the free phase, because the newly created packets are less than the delivered packets, η (R) is around zero. With the increase of packet generation rate R, there will be a critical packet generating rate Rc indicating that the phase transition will occur from the free phase to the congestion phase. When R > Rc, the packets accumulate continuously in the network and η (R) will increase from zero. Thus the network capacity can be represented by the critical value of packet generating rate Rc at the phase-transition point.
In our simulation environment, we assume that both upper layer and lower layer have the same network size N. The upper layer and the lower layer are geographically divided into 3 × 3 square districts (except Fig. 5), and each district is in unit side length.
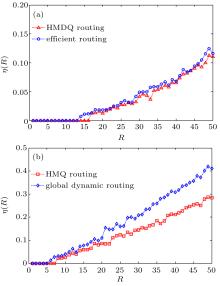
In Fig. 2, we show the relation of order parameter η (R) vs packet generation rate R under different routing strategies. For all cases considered, one can see that η (R) is approximately zero when R < Rc, and then it increases from zero when R > Rc. Specifically, Figure 2(a) shows the network capacity comparison between HMDQ routing strategy and efficient routing strategy. It can be seen that the network capacity of efficient routing strategy under traffic concurrency space stereo multi-layer scale-free network is Rc = 13. The HMDQ routing strategy reaches a very high capacity of Rc = 16, which is increased by 23% compared with efficient routing strategy. Figure 2(b) compares the network capacity between HMQ routing strategy and global dynamic routing strategy. It is clear that the global dynamic routing strategy has Rc = 5 and HMDQ routing strategy reaches Rc = 7, which is increased by 40%. As far as we know, the forward-predicting Qp (xm) can further balance the traffic distribution and make the delivery of packets avoid the congestion nodes beforehand in traffic concurrency network. In addition, we can find that the network capacity of efficient routing strategy is higher than global dynamic routing strategy. In our opinion, lots of new created packets would cross the same nodes that satisfy the requirement of minimum queue length synchronously in global dynamic routing strategy, and it will lead to serious network congestion. Whereas in the efficient routing strategy, as the limitation of node degree, the number of packets that cross the same nodes is fewer and this relieves the network congestion to some extent. Affected by this reason, the network capacity of HMDQ routing strategy is higher than HMQ routing strategy too. The rank of network capacity is HMDQ routing strategy > efficient routing strategy > HMQ routing strategy > global dynamic routing strategy.
Figure 3 shows the relation of Δ N(p) versus packet generation rate R under different routing strategies. From Fig. 3(a), we can see that with the increase of packet generation rate R, the Δ N(p) of efficient routing strategy and HMDQ routing strategy is larger than zero when R = 13 and R = 16, respectively. In Fig. 3(b), the Δ N(p) of global dynamic routing strategy and HMQ routing strategy increases from zero when R = 5 and R = 7 respectively. Combing Figs. 3(a) and 3(b), one can see that the rank of Δ N(p) is global dynamic routing strategy > HMQ routing strategy > efficient routing strategy > HMDQ routing strategy. The larger Δ N(p) means more packets are congested and needed to be handled during time windows Δ t. It is obvious that the forward-predicting strategy can make the network support larger packet generation rate R and attenuate the network congestion in both free phase and congestion phase for the circumstance of traffic concurrency. This explains the reasons for the rank of network capacity Rc.
 | Fig. 4. Network capacity Rc under different routing strategies. 〈 Kupper layer〉 = 8, 〈 Kinter-layer〉 = 4, and C = 2. |
Figure 4 gives the relation of network capacity Rc versus the network size N under different routing strategies. The HMDQ routing strategy and HMQ routing strategy can obtain better performances than efficient routing strategy and global dynamic routing strategy respectively. The forward-predicting strategy can bring remarkable effects on improving the network capacity. It also can be seen that with the increase of network size N, the network capacity of all routing strategies increases obviously. In our opinion, with the growth of network size N, there are more available routes existing in the network, and these redundant routes will alleviate the pressure of congestion nodes in handling the newly created packets, which will obtain the improvement of network capacity for different routing strategies. Then, the phase steps appear in Fig. 4.
As the number of districts can affect the network performance, we divide the upper layer and lower layer into 2 × 2 square districts. From Figs. 5(a) and 5(b), we can see that the network capacity still meets the rule: HMDQ routing strategy > efficient routing strategy > HMQ routing strategy > global dynamic routing strategy. However, compared with the 3 × 3 geographical division pattern, the network capacity of HMDQ routing strategy, efficient routing strategy, HMQ routing strategy and global dynamic routing strategy reduces about 12.5%, 15.4%, 28.6%, and 20% respectively. In our opinion, with the decrease of the number of geographical districts, the number of nodes that located in one district will increase. These nodes will bring more packets to one district, and these packets will travel through the congestion nodes of one district of scale-free network, which will aggravate the network congestion and then decrease the network capacity.
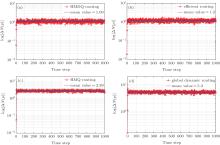
To further explain the effects of forward-predicting strategy on traffic concurrency space stereo multi-layer scale-free network, we investigate the time evolution of Δ N(p) in congestion phase. As Rc < R = 30, the packets congest in the network synchronously, and accumulate continuously. By comparing Figs. 6(a) and 6(b), we can see that the mean value of Δ N(p) is 1.2 in efficient routing strategy, and this value decreases to 1.09 in HMDQ routing strategy. Comparing Fig. 6(c) with Fig. 6(d), the mean value of Δ N(p) reduces from 5.2 to 2.89. That is to say, the existence of forward-predicting strategy makes the allocation of network routing resource reasonable, avoids the traffic transmission along the same nodes and decreases the network burden on transmitting congested packets, which can bring high efficiency on the delivery of packets in traffic concurrency space stereo multi-layer scale-free network. This illustrates that the forward-predicting strategy plays an active role in the alleviation of traffic congestion.
Finally, we investigate the properties of packet distribution vs. node degree. Figure 7(a) shows the dependence of probability distribution P(k) of packets on node degree K for HMDQ routing strategy and efficient routing strategy. As the routing selection of efficient routing strategy only relies on the node degree, we can find that the packets mainly assemble in the nodes with small degree. In the HMDQ routing strategy, although the probability distribution P(k) is close to the situation of efficient routing strategy, the existence of forward-predicting Qp (xm) makes the P(k) extend to the large degree nodes, which is helpful to reduce the traffic congestion. Figure 7(b) shows the probability distribution P(k) for HMQ routing strategy and global dynamic routing strategy. For both routing strategies focus on the minimum queue length, they possess the similar distribution properties. The packets are almost distributed around all the node degree. The probability P(k) gives us a better understanding on the packet distribution in the traffic concurrency space stereo multi-layer scale-free network. The effects of forward-predicting strategy are further presented in Figs. 7(c) and 7(d). Figure 7(c) shows the packet number distribution n(k) versus node degree K for HMDQ routing strategy and efficient routing strategy. One can see that even though the probability distribution P(k) of both routing strategies is close to each other, the number of congested packets of HMDQ routing strategy is obviously less than efficient routing strategy. This circumstance also happens in Fig. 7(d). Figure 7 proves that the proposed forward-predicting strategies can enhance the network capacity, balance the traffic distribution, reduce the number of congested packets and improve the network performance again.
As many communication networks, such as oceanic monitoring network and land environment observation network, are space stereo multi-layer and the traffic is usually concurrent in modern communication systems, in this paper, we proposed a traffic model of space stereo multi-layer complex network and introduced two kinds of global forward-predicting dynamic routing strategies, global forward-predicting hybrid minimum queue (HMQ) routing strategy and global forward-predicting hybrid minimum degree and queue (HMDQ) routing strategy, for traffic concurrency space stereo multi-layer scale-free networks. Compared with the efficient routing strategy and global dynamic routing strategy, the proposed routing strategies can achieve better performances in traffic concurrency space stereo multi-layer scale-free networks. Numerical simulation results show that the HMDQ and HMQ routing strategies can balance the traffic distribution, alleviate the number of congested packets effectively and reach much higher network capacity. Since the traffic dynamics is crucial for many real communication networks, we believe that such insights will be useful for design and optimization of network traffic performances.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|