†Corresponding author. E-mail: aihuahu@126.com
*Project supported by the National Natural Science Foundation of China (Grant No. 11202084).
This paper investigates event-triggered synchronization for complex networks with Markovian jumping parameters. Nonlinear dynamics with Markovian jumping parameters is considered for each node in a complex network. By utilizing the proposed event-triggered strategy, and based on the Lyapunov functional method and linear matrix inequality technology, some sufficient conditions for synchronization of complex networks are derived whether the transition rate matrix for the Markov process is completely known or not. Finally, a numerical example is presented to illustrate the effectiveness of the proposed theoretical results.
In the past few decades, the research of complex dynamical networks has been a hot topic in various fields. Many practical systems in the real world can be described by models of complex networks. Particularly, synchronization as one of the interesting phenomena in complex networks has received considerable attention due to its wide applications in computer science, life science, control engineering, and so on.[1– 4] Up to now, several types of synchronization have been studied by researchers, such as complete synchronization, [5, 6] generalized synchronization, [7, 8] the lag synchronization, [9] and hybrid projective synchronization.[10] Meanwhile, many control methods have been proposed for guaranteeing the synchronization. Since practical networks usually have the limited bandwidth of the communication, sampled-data control is an effective approach.[11, 12] Yu et al.[11] explored the secondorder consensus in multi-agent dynamical systems with sampled position data, and Rakkiyappan et al.[12] analyzed exponential synchronization of complex dynamical networks by using the sampled-data approach. Generally speaking, a controller in the sampled-data scheme is updated regularly with a constant sampling period. Therefore, the sampled-data control is also regarded as time-triggered control. However, the periodical updating in time-triggered control happens whether it is necessary or not, which may lead to higher cost. Correspondingly, it is important to design a good control strategy in order to save communication and computation resources.
Recently, event-triggered control as an alternative of the time-triggered control, has been extensively explored. Compared with continuous communication, [13– 15] communication in an event-triggered framework can be discrete, which is more practical; furthermore, fewer communication resources may be utilized compared with the time-triggered control. In an event-triggered scheme, an event will be triggered if the given triggering condition holds, and the occurrence of the event will determine control actuation updates. Moreover, it should be noted that the information among neighboring nodes in a network can be transmitted aperiodically, which can avoid congestion of the network. At present, some works have studied the effectiveness of synchronization in complex networks with event-triggered control, such as event based agreement protocols for multi-agent networks have been discussed in Ref. [16] and event-triggered average consensus control for discretetime multi-agent systems has been studied in Ref. [17]. An event-triggered communication scheme to deal with the state estimation problem in an unstable networked control system has been proposed.[18] On the other hand, the Zeno behavior may exist in a system with event-triggered control, which means that there are infinite switching numbers in the finite time. Accordingly, the Zeno behavior can cause the chattering phenomenon, then the system under control will become unstable. The event detector in Ref. [19] has a sampling period, which implies that Zeno behavior is excluded. More literature on Zeno behavior can be reviewed.[20, 21] In addition, by utilizing the event-triggered scheme, networked control systems with communication delay were discussed, [22] and Luo et al.[23] investigated the complete synchronization of chaotic systems with only one state variable information from the drive system, which is more realistic and practical.
As is well known, nonlinear dynamics widely exists in practical systems. Such nonlinear dynamics may be subject to some abrupt and random variations induced by environmental circumstances. Therefore, research on synchronization of complex networks with nonlinear dynamics has practical significance.[24, 25] Reference [24] studied multi-agent systems with inherent nonlinear dynamics under directed topologies, and reference [25] focused the synchronization for higherorder nonlinear systems. Moreover, the dynamical systems can be described by stochastic hybrid systems due to random factors. Particularly, Markovian jumping systems as a special class of hybrid systems have been studied in the past few years, and many profound results have been established.[26– 29] In Ref. [26], authors have investigated exponential state estimation of Markovian jumping genetic regulatory networks with mode-dependent probabilistic time-varying delays. In Refs. [27]– [29], the authors have analyzed the stability of Markovian jumping stochastic neural networks. To the best of the authors’ knowledge, synchronization of Markovian jumping complex networks with event-triggered control has rarely been considered so far. Additionally, the information on transition probabilities in the Markovian switching process is usually assumed to be completely known in the previous literature. However, it is difficult to obtain completely known transition probabilities usually. Fortunately, Markovian jumping systems with partly known transition probabilities have been investigated in some references.[30– 32]
Motivated by the above discussion, in this paper, synchronization of Markovian jumping complex networks with eventtriggered control is considered. Suppose that the communication topology is strongly connected, we consider nonlinear dynamics with Markovian jumping parameters for each node in a complex network. Furthermore, the transition rates for the Markov process are considered to be completely known and partly known, respectively. Then the sufficient conditions are proposed for synchronizing the network. Finally, some numerical simulations are shown to illustrate the theoretical results. The rest of the paper is organized as follows. In Section 2, some preliminaries and a description of the system are presented. The main results are given in Section 3. In Section 4, one numerical example is used to verify the effectiveness of the proposed theoretical results. Conclusions are drawn in Section 5.
Throughout this paper, ℛ n denotes n-dimensional Euclidean space, and ℛ n× n is the set of all n × n real matrices. Let ℕ be the set of natural numbers. The superscript T and ⊗ represent matrix transposition and the Kronecker product, respectively. The sign In denotes an n × n identity matrix, and 1N denotes the N-dimensional column vector with each entry being 1. ∥ · ∥ stands for the Euclidean vector. * denotes the elements below the main diagonal of a symmetric matrix. diag{...} represents the block diagonal matrix, 
The 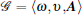
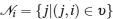

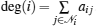
Consider that a complex dynamic network consists of N identical coupled nodes and each node moves according to the following dynamics:
where xi(t) ∈ ℛ n and ui(t) ∈ ℛ n are the state variable and the control input of the node i, respectively, A(r(t)) ∈ ℛ n× n and B(r(t)) ∈ ℛ n× n are constant matrices, and f(xi(t), t) ∈ ℛ n denotes the nonlinear dynamics of the i-th node.
Let 
where Δ > 0 and 
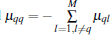
We propose the following event-triggered controller:
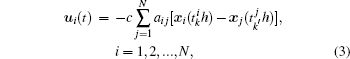
where 
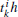

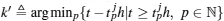
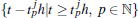

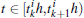
The event-triggered condition (or the event detector) of node i is given by
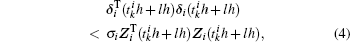
where k, l ∈ ℕ , σ i > 0, i = 1, 2, ..., N is the trigger parameter. 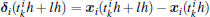
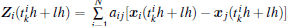
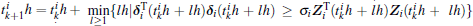

Remark 1 If 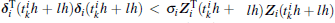

Remark 2 In this paper, the event-triggered transmission strategy proposed is discrete. We only need to broadcast neighbors’ sampled-date for the node i and examine the eventtriggered condition at each sampling period h, which can reduce the computation burden and conserve resources.
Remark 3 In this paper, the inter-event time has a minimum bound by the sampling period h > 0 to exclude the Zeno behavior.
Substituting Eq. (3) into Eq. (1) gives

where 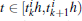
In order to obtain our theoretical results, the following assumption and lemmas are given.
Assumption 1 Suppose f in Eq. (1) is a bounded nonlinear function, and the following Lipschitz condition is satisfied:
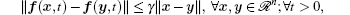
where γ represents a Lipschitz constant.
Lemma 1[33] Suppose that a directed graph 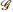
Lemma 2[34] For any constant matrix R ∈ ℛ n× n, R = RT > 0, and M ∈ ℛ n× k, time-varying function τ (t) satisfying 0 < τ (t) ≤ h, and vector function ż :[− h, 0] → ℛ n such that the following integration is well defined, let 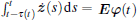
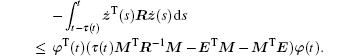
Lemma 3[35] The following linear matrix inequality (LMI)

where 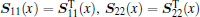
(i) 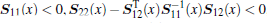
(ii) 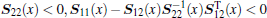
Definition 1 The complex dynamic network (1) is said to achieve mean square synchronization, if the following condition is satisfied for any initial condition xi(0) ∈ ℛ n:

In this section, the sufficient conditions for mean square synchronization of the complex dynamic network (1) will be given.
Denote 
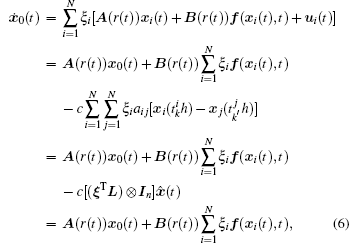
where 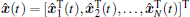
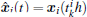
Let ei(t) = xi(t) − x0(t) (i = 1, 2, ..., N) be the position vector error between the i-th node and the weighted average of all the nodes in system (1). Then, according to the Eqs. (5) and (6) and the definition of measurement error 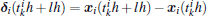
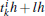
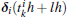
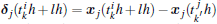
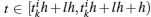


the above equation is satisfied due to ξ T1N = 1 based on Lemma 1. Moreover, all the triggered instants are a subsequence of the sampled instants, which means that the event instants 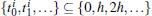
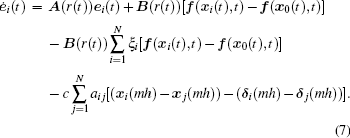
Now, for t ∈ [mh, (m+ 1)h), we define τ (t) = t – mh as an “ artificial delay” . Clearly, 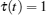

where
For the following Theorem 1, ɛ i ∈ ℛ 5Nn× Nn (i = 1, 2, ..., 5) are defined as block entry matrices, e.g., 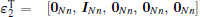
Theorem 1 Under Assumption 1, and suppose that the network is strongly connected. Then for some given positive scalars c and h, the complex dynamic network (1) can achieve mean square synchronization under the event-triggered controller (3), if there exist appropriate dimensional matrices Pq > 0, Q > 0, R > 0, Y > 0, U, and V, such that the following linear matrix inequalities hold for arbitrary q = 1, 2, ..., M,
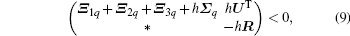
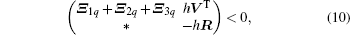
where
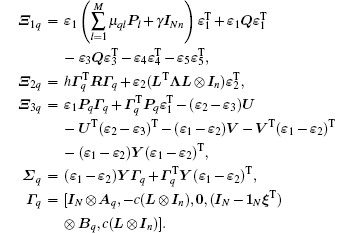
Proof For t ∈ [mh, (m+ 1)h), we choose a Lyapunov– Krasovskii function as
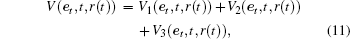
where

The infinitesimal operator ℒ of V(et, t, r(t) = q) is defined as follows:
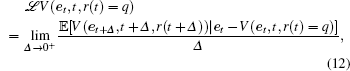
then,
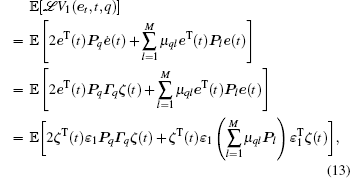
where
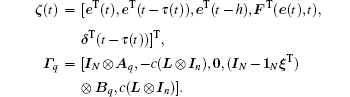
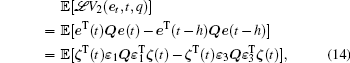
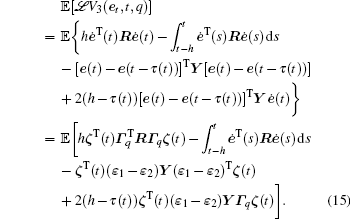
Moreover,
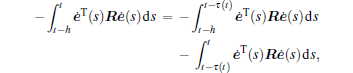
and
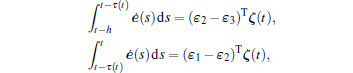
by combining Lemma 2, we have
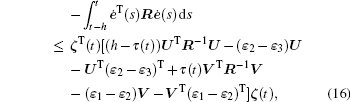
where U and V are matrices with appropriate dimensions.

Due to the fact that
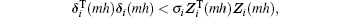
thus
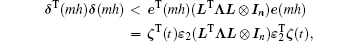
where Λ = diag{σ 1, σ 2, ..., σ N}. Therefore, we have
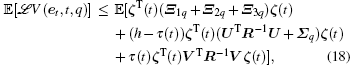
where Ξ 1q, Ξ 2q, Ξ 3q, and Σ q are defined in Theorem 1.
By Lemma 3 in Eqs. (9) and (10), the following inequalities hold:
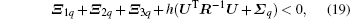
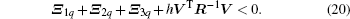
Clearly, Ξ 1q + Ξ 2q + Ξ 3q + (h – τ (t))Φ 1 + τ (t)Φ 2 is a convex combination of Φ 1 and Φ 2 on τ (t) ∈ [0, h), where Φ 1 = UTR− 1U + Σ q, Φ 2 = VTR− 1V. Therefore, we can conclude that 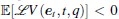
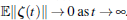
In practice, the transition rates for the Markov process are partly known in most cases. Therefore, it is necessary to study jump systems with partly known transition probabilities. Then, the results of Theorem 1 are extended to the case of transition probabilities being partly known as the following corollary.
For system (1) in this paper, the transition rate matrix with partly unknown probabilities is given by
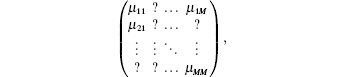
where ? denotes the unknown transition rate. We let 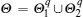

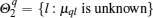
Corollary 1 Under Assumption 1, and suppose that the network is strongly connected. For some given positive scalars c and h, the complex dynamic network (1) can achieve mean square synchronization under the event-triggered controller (3), if there exist appropriate dimensional matrices Pq > 0, Q > 0, R > 0, Y > 0, U, V and symmetric matrix Zq, such that the following linear matrix inequalities hold for arbitrary q = 1, 2, ..., M:
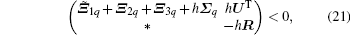

where

Proof We choose the same Lyapunov– Krasovskii function as that of Theorem 1, and also have the following equation:
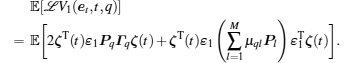
Due to 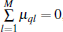
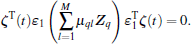
Thus
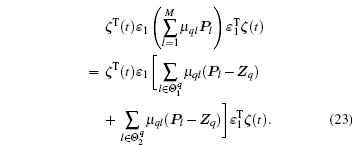
Moreover,
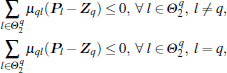
then, the following equation holds:
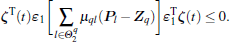
According to the above analysis, we obtain
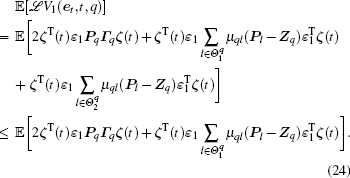
Since 
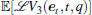
In this section, one numerical example is provided to illustrate the effectiveness of the theoretical results.
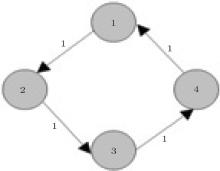
Consider that a network of four nodes can be described by the system (1) and its communication topology 
Let Θ = {1, 2, 3}, then choose the parameters of the system (1) as follows:

The Laplacian matrix L is given by
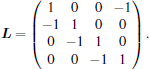
The event-triggered controller is designed under the event-triggered transmission strategy. Set the sampling period h = 0.01 s and the event-triggered parameters σ 1 = 0.025, σ 2 = 0.015, σ 3 = 0.02, and σ 4 = 0.016. Let the control gain c = 2 and the Lipschitz constant γ = 0.1, respectively.
The partly transition rate matrix is given by
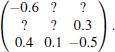
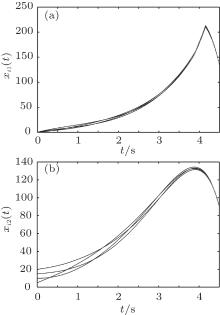
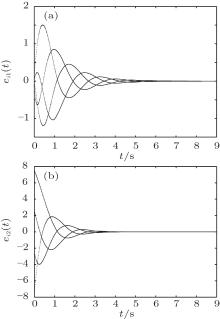
By utilizing the LMI toolbox, the feasible solutions are obtained. The initial states of the system are given as xi(0) = [0.1i, 5i]T. The state trajectories of the system in Figs. 2(a) and 2(b) depict the states of xi1 and xi2 (i = 1, 2, 3, 4), respectively. Moreover, the synchronization errors ei(t) = xi(t)-x0(t) (i = 1, 2, 3, 4) are shown in Fig. 3, where 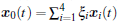
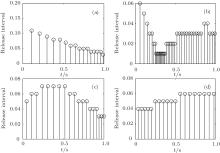 | Fig. 4. Event-triggered instants and intervals of the i-th node (a) i = 1; (b) i = 2; (c) i = 3; (d) i = 4. |
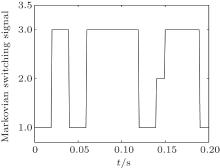
In addition, the Markovian switching signal r(t) is shown in Fig. 5, which depicts the switching between three subsystems.
In this paper, the synchronization problem of Markovian jumping complex networks with event-triggered control has been investigated. The network topology is supposed to be strongly connected, and nonlinear dynamics with Markovian jumping parameters is considered for each node in the network. Moreover, we extend the results to the system with partly known transition probabilities, and the proposed results are demonstrated by the form of linear matrix inequalities (LMIs). A numerical example is given to illustrate the effectiveness of the presented theoretical results. We will further study systems with noise disturbances in the future.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|