†Corresponding author. E-mail: jshen@mail.ipc.ac.cn
‡Corresponding author. E-mail: tangcc@hebut.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 51322605 and 51271192).
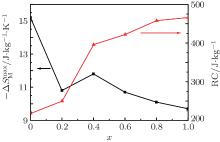
The magnetism and magnetocaloric effect in Er1 − xGd xCoAl ( x = 0, 0.1, 0.2, 0.4, 0.6, 0.8, 1) were investigated. The Er1 − xGd xCoAl compounds were synthesized by arc melting. With the increasing Gd content, the Néel temperature ( TN) linearly increases from 14 K to 102 K, while the magnetic entropy change (−Δ SM) tends to decrease nonmonotonously. Under the field change from 0 T to 5 T, the −Δ SM of the compounds with x = 0.2–1 are stable around 10 J/kg ·K, then a cooling platform between 20 K and 100 K can be formed by combining these compounds. For x = 0.6, 0.8, 1.0, the compounds undergo two successive magnetic transitions, one antiferromagnetism to ferromagnetism and the other ferromagnetism to paramagnetism, with increasing temperature. The two continuous magnetic transitions in this series are advantageous to broaden the temperature span of half-peak width (δ T) in the −Δ SM− T curve and improve the refrigeration capacity.
Magnetic refrigeration is a potential cooling technology due to its higher energy efficiency and lower environmental impact than the conventional vapor compression refrigeration.[1] The feasibility of applying this technology highly depends on the design and synthesis of suitable magnetic cooling materials. For a long time, looking for a high magnetic entropy change (− Δ SM) was regarded as the primary task.[2– 4] A large number of materials with first-order magnetic transition, such as LaFe13− xSix, [5– 7] MnAs1− xSbx, [8, 9] MnFePxAs1 − x, [10– 12] and Mn1 − xFexAs, [13] have been found to exhibit the giant magnetocaloric effect (MCE). However, the magnetic entropy change is not the only parameter to evaluate the cooling capacity of a refrigerant material. The refrigerant capacity 
It has been reported that the RCoAl (R = Gd, Tb, Dy, Ho) compound shows a large magnetic entropy change in a wide temperature span near the transition temperature.[15] For example, in the soft magnetic GdCoAl compound, a table-like behavior from 70 K to 105 K was found in the temperature dependence of − Δ SM. These compounds crystallize in the MgZn2-type hexagonal structure with ordered temperatures in the range from 10 K to 100 K. Especially, the GdCoAl compound has a ferromagnetic transition at 100 K.[16] It crystallizes in the hexagonal MgZn2 structure (space group P63/mmc), which is a close-packed laves phase. The absence of magnetic moment on Co was reported despite the fact that the 3d shell of Co is not completely filled.[17] This means that only the S-state Gd3+ ions contribute to the magnetic properties of GdCoAl. In other derived compounds such as Gd2Co2Al and GdCo0.74Al1.26, the metamagnetic transition of ferromagnetic transition and the glassy phase near 80 K result in the occurrence of a table-like magnetocaloric effect with a magnitude of − 7 J/kg· K over the temperature range from 47.5 K to 77.5 K for a magnetic field variation from 0 T to 5 T.[18] In this work, we introduce continuous magnetic transitions in the compounds by the substitution of different rare earth elements, which broaden the − Δ SM temperature span. The polycrystalline Er1 − xGdxCoAl (x = 0– 1) compounds are synthesized and their magnetic properties and MCE properties are investigated. With the substitution of Gd for Er, TN increases and − Δ SM exhibits a decreasing trend, however, RC is improved, which originates from the broadened temperature span (δ T) in the − Δ SM− T curve.
The polycrystalline samples of Er1 − xGdxCoAl (x = 0, 0.2, 0.4, 0.6, 0.8, 1) were synthesized by arc melting of stoichiometric amounts of the elements with purity 99.9 wt.% in a water-cooled copper hearth under a purified argon atmosphere. The weight of rare earth metal R was 3% more than the theoretical value in order to compensate the loss. The samples were remelted three times to ensure the homogeneity. The samples were annealed at 1123 K for 10 days in a quartz tube with a high vacuum, and a subsequent quenching to room temperature was performed to obtain crystalline samples. Powder x-ray diffraction (XRD) measurements were performed at room temperature by using Cu Kα radiation to identify the crystal structure. The x-ray powder diffraction patterns showed that the Er1 − xGdxCoAl (x = 0, 0.2, 0.4, 0.6, 0.8, 1) compounds crystallize in the MgZn2-type hexagonal structure and no impurity phases were detected. Magnetization measurements were carried out by employing a commercial superconducting quantum interference device (SQUID) magnetometer, model MPMS-7 from Quantum Design Inc.
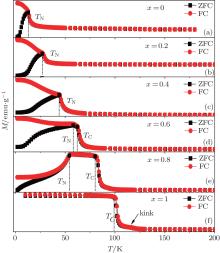
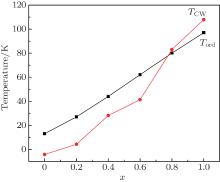
Figure 1 shows the temperature dependences of magnetization for the Er1 − xGdxCoAl (x = 0, 0.2, 0.4, 0.6, 0.8, 1) compounds under zero-field-cooling (ZFC) and field-cooling (FC) with a magnetic field of 0.01 T. The ZFC curves show that the transition temperature increases from 14 K to 102 K as the content of Gd increases, as shown in Fig. 2. With increasing temperature, ErCoAl exhibits an AFM– PM magnetic transition at TN = 14 K (Fig. 1(a)), this is similar to the cases of x = 0.2, 0.4 (Figs. 1(b) and 1(c)). With the substitution of Gd for Er, the compound with x = 0.6 exhibits two successive magnetic transitions, i.e., a transition from AFM to FM at TN = 53 K and a transition from FM to PM at TC= 58 K (Fig. 1(d)). From Fig. 1(d), one can see that the magnetization increases rapidly below 11 K and slowly in the range of 11– 53 K upon temperature increasing, indicating the occurrence of magnetic phase separation of FM and AFM at low temperature. As shown in Fig. 1(f), no thermal hysteresis is observed for the GdCoAl compound, while a bifurcation is observed between ZFC and FC curves below TC which should be related to the domain effect during the field cooling process. A small kink is observed around 117 K in the GdCoAl compound, which may be caused by the partial FM clusters.
The magnetization data above 150 K of all samples can be well fitted using the Curie– Weiss law with the expression χ − 1 = (T − θ )/C, where θ denotes the Weiss constant and C is the Curie constant. Figure 2 shows the Gd doping x dependence of Curie temperature Tord and Curie– Weiss temperature TCW. One can see that both the Curie– Weiss temperature and the ordered temperature increase with increasing x, suggesting an increase of the ferromagnetic interaction due to the contribution from the Gd sublattice. Based on the formula μ eff = (3kBC/NA)1 / 2 (kB and NA being the Boltzmann constant and the Avogadro constant), the paramagnetic effective magnetic moment μ eff can also be determined. The μ eff seems to show an increasing trend with x to 0.6 then starts to drop, while the theoretical value obtained according to the formula 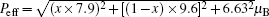
Magnetization isotherms of the Er1 − xGdxCoAl (x= 0, 0.2, 0.4, 0.6, 0.8, 1) compounds were measured at different low temperatures under applied fields up to 1.5 T, as shown in Fig. 3. All the compounds show antiferromagnetic like characteristics since the saturation is not reached at 5 T except GdCoAl, which shows a ferromagnetic feature. As shown in Fig. 3(f), the magnetization increases linearly with the increase of the magnetic field in the low field range, then the magnetization increases rapidly with increasing magnetic field and saturates quickly. It confirms the field-induced metamagnetic transition from AFM to FM state and finally the FM state is obtained as the magnetic field approaches ∼ 1 T. The magnetic moment per formula Ms at 5 T and 5 K is calculated, which increases with the Gd content x. Theoretically, the magnetic moment of Er is larger than that of Gd and the total magnetic moment should be reduced by the gradual replacement of Gd for Er. However, the total magnetic moment is increased at low temperature, which implies that the introduction of Gd at the Er position brings about the magnetic moment arranged partially parallel with Er or the induced crystal field change results in Co spin moment reorientation. At the same time, the exchange of AFM or the magnetic anisotropy may be reduced as well. For example, the element Er was used to cancel the anisotropy of Dy, since the Stevens factors of Dy and Er have opposite signs.[19] Therefore, the magnetic property is changed and the total magnetic moment exhibits a complex phenomenon either in high or low temperatures with the substitution of Gd for Er.
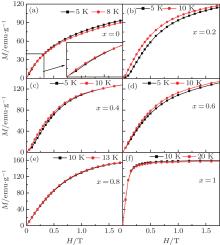 | Fig. 3. Magnetization isotherms of Er1 − xGdxCoAl (x= 0, 0.2, 0.4, 0.6, 0.8, 1) compounds measured at low temperature. |
The isothermal magnetic entropy changes − Δ SM of Er1− xGdxCoAl (x = 0– 1) are obtained from the experimental isothermal magnetization data by using the Maxwell relation 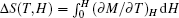
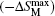
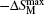
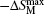
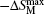
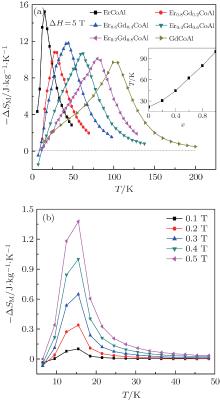
As described above, the compounds with x = 0.6 and 0.8 exhibit two successive magnetic transitions as shown in Figs. 1(d) and 1(e), respectively. However, only one peak in the − Δ SM– T curve is observed in Fig. 4. To explain this phenomenon, the magnetic entropy changes as a function of temperature for the Er0.4Gd0.6CoAl and Er0.2Gd0.8CoAl compounds under low magnetic field are shown in Fig. 5. Two peaks are observed under low magnetic field (0.1– 0.5 T) for Er0.2Gd0.8CoAl, which correspond to the two magnetic transitions. The − Δ SM is mainly caused by the FM– PM transition, whereas the AFM– FM transition contributes to the half maximum of the peak width of − Δ SM. Meanwhile, with increasing magnetic field (Figs. 5(a) and 5(b)), the contribution to − Δ SM from the FM– PM transition sharply increases, while that from the AFM– FM transition increases gently. With increasing the Gd content, the temperature span is increased due to the improvement of the AFM– FM transition upon warming. A slight depression of − Δ SM seems to be responsible for the broadened temperature span with increasing x.
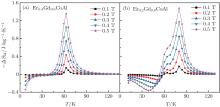 | Fig. 5. Temperature dependences of magnetic entropy change in Er0.4Gd0.6CoAl and Er0.2Gd0.8CoAl with different magnetic field changes. |
The RC is considered to be an important parameter of a potential magnetic refrigerant. The RC is a measure of how much heat could be transferred between the hot and cold reservoirs in an ideal refrigerant cycle and a large RC is desirable. The RC is calculated by numerically integrating the area under the − Δ SM– T curve, 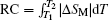
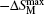
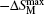
The magnetic and magnetocaloric properties of the Er1 − xGdxCoAl (x= 0, 0.1, 0.2, 0.4, 0.6, 0.8, 1) compounds were investigated. The temperature dependence of magnetization showed that the introduction of Gd increases the magnetic transition temperature from 14 K to 102 K. The 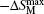
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|