Cite this Article
Chakraverty S†, Behera Laxmi. Vibration and buckling analyses of nanobeams embedded in an elastic medium. Chinese Physics B, 24(9): 097305  
Permissions
Vibration and buckling analyses of nanobeams embedded in an elastic medium
Chakraverty S†, Behera Laxmi
Department of Mathematics, National Institute of Technology Rourkela, Odisha, India

†Corresponding author. E-mail: snechak@gmail.com

Abstract

Boundary characteristic orthogonal polynomials are used as shape functions in the Rayleigh–Ritz method to investigate vibration and buckling of nanobeams embedded in an elastic medium. The present formulation is based on the nonlocal Euler–Bernoulli beam theory. The eigen value equation is developed for the buckling and vibration analyses. The orthogonal property of these polynomials makes the computation easier with less computational effort. It is observed that the frequency and critical buckling load parameters are dependent on the temperature, elastic medium, small scale coefficient, and length-to-diameter ratio. These observations are useful in the mechanical design of devices that use carbon nanotubes.

PACS: 73.63.Fg; 65.80.–g; 66.70.Lm; 02.60.–x
Keyword: Rayleigh–Ritz method; boundary characteristic orthogonal polynomials; nonlocal elasticity theory; Euler–Bernoulli beam theory
1. Introduction

Recently, nanomaterials have aroused interest among the scientific communities in the fields of physics, chemistry, and engineering. Some of these materials are nanoparticles, nanowires, [1– 4] nanotubes, [5– 15] and nanotube resonators. Among them, beam type structures play a vital role in the field of nanotechnology. The discovery of carbon nanotubes by Ijima[16] has sparked a revolution in nanotechnology. Because of the unique characteristics of carbon nanotubes, [17] they have been recognized as promising materials for future applications such as nanodevices, nanocomposites, and nanoelectronics. Conducting experiments at nanoscale size is quite difficult. Molecular dynamics is one of the effective ways to study the mechanical properties of nanostructures. But the molecular dynamics simulation is time consuming and arduous for large-scaled CNTs. Accordingly, classical continuum mechanics is being increasingly viewed as an efficient way to study nanostructured materials. But these continuum models do not capture small scale effects. Hence various nonlocal continuum theories have been proposed to study mechanical behaviors of structures at nanoscale. One of the nonlocal continuum theories is the nonlocal elasticity theory pioneered by Eringen.[18] Beam and shell models have been developed based on the nonlocal elasticity theory to model nanostructures. Peddieson et al.[19] applied the nonlocal continuum model to nanotechnology. Xu[20] found that the nonlocal effect has significant influences on the natural frequency and vibration modes in nanostructures. Since conducting experiments at nanoscale size is quite difficult, development of mathematical models is necessary. Hence analytical and numerical methods have been developed by the authors to investigate static and dynamic problems of nanobeams.[21– 26] Study of various aspects of nanotubes such as buckling, mechanical, chemical, and thermal properties attracts tremendous attention of researchers. Thermal effects are significant in vibration and buckling analyses since the increase in temperature leads to the increase in carbon– carbon (C– C) bond length in the CNTs, which induces an axial and radial force within CNTs. Thermal vibration frequencies may be used to estimate Young’ s modulus of various nanotubes.[27] Therefore, the investigation of the thermal effect on the mechanical properties of CNTs is very important. Moreover, the surrounding elastic medium has a great influence on the frequencies and buckling loads of carbon nanotubes. Some researchers have considered the thermal effect in the vibration and buckling analyses of nanotubes. A few of them are cited below.

Free vibration of single-walled carbon nanotubes (SWCNTs) has been investigated based on the nonlocal Levinson beam theory[27] and the Timoshenko beam theory[28, 29] in a thermal environment. The authors found that vibration characteristics are strongly dependent on the temperature change. Similar thermal effect may also be seen when one analyzes the instability of SWCNTs conveying fluid.[30] The thermal effect on the vibration of double-walled carbon nanotubes has been investigated analytically by Zhang et al.[31] for simply supported edge condition. The differential quadrature method has been employed by Murmu and Pradhan[32] to study thermo mechanical vibration of SWCNTs embedded in an elastic medium. The authors applied the same method for buckling analysis of SWCNTs embedded in an elastic medium[33] based on the nonlocal Timoshenko beam theory. Buckling analysis of SWCNTs embedded in an elastic medium has also been presented analytically by Narendar and Gopalakrishnan[34] in a thermal environment. Thermal buckling analysis of embedded SWCNTs has also been investigated in Refs. [35] and [36]. Tounsi et al.[37] analyzed buckling behavior of nanobeams based on the higher order beam theory.

Recently, efforts have been made by the researchers to develop efficient numerical and analytical methods for obtaining desired results with ease. Numerical methods such as differential quadrature and finite element have been applied with simple boundary conditions such as simply supported. However, it is sometimes tedious to apply such numerical methods in the complicated problems for all sets of boundary conditions. In this context, one may use the Rayleigh– Ritz method (R– R), which is quite easy to handle for all classical boundary conditions. Previously, authors have applied boundary characteristic orthogonal polynomials as shape functions in the R– R method to analyze static and dynamic problems of beam or plate elements.[38– 43] However, to the best of our knowledge, this is the first attempt on the application of the R– R method for the vibration and buckling analysis of nanobeams embedded in an elastic medium under the influence of temperature. In this article, boundary characteristic polynomials are implemented in the R– R method. The use of boundary characteristic polynomials in the R– R method produces results with high accuracy, stable computation, and rapid convergence. Because of the orthogonal property of boundary characteristic polynomials, some of the entries of stiffness and mass matrices become either zero or one. Effects of the surrounding elastic medium, temperature, nonlocal parameter, and lengthto- diameter ratio on the frequency and critical buckling load parameters are systematically analyzed.

2. Problem formulation

This study is carried out on the basis of the Euler– Bernoulli beam theory in conjunction with the nonlocal elasticity theory of Eringen.[18] For applying the present method, one needs to have knowledge about energies. Therefore, at first we have given an overview of the energies of nanobeams based on the Euler– Bernoulli beam theory. Here the x coordinate is taken along the length of the beam and the z coordinate is measured from the mid-plane of the beam.

2.1. Euler– Bernoulli beam theory

The strain energy U may be written as

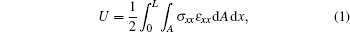
where σ xx is the normal stress, L is the length of the beam, and A is the cross-section area. Here normal strain ε xx is given by the following relationship:

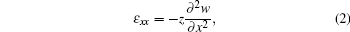
where w is the deflection function. Substituting Eq. (2) in Eq. (1), we obtain

where M is the bending moment and is defined as M = ∫ Azσ xxdA. Assuming free harmonic motion, i.e., w = w0(x) sin ω t, where ω is the natural frequency of vibration, one may obtain strain energy U as

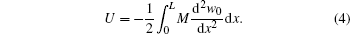
The kinetic energy is given as

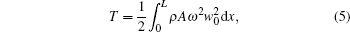
where ρ is the mass density of beams.

The potential energy (the work done by external forces) may be given as[44]

where N̄ is the applied compressive force and is expressed as N̄ = Nm + Nθ . Here Nm is the axial force due to the mechanical loading prior to buckling, and Nθ is the axial force due to the influence of the temperature change, Nθ = − EAα xθ /(1 − 2ν ), where E is the Young’ s modulus, A is the cross-section area, ν is the Poisson’ s ratio, α x is the coefficient of thermal expansion in the x direction, and θ is the change in temperature. The fe is the density of reaction force of elastic foundation which is expressed as fe = kww0 − kgd2w0/dx2. Here kw denotes the Winkler modulus and kg denotes the shear modulus of the elastic medium.

Using Hamilton’ s principle

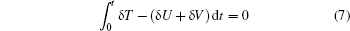
and setting the coefficient of δ w0 to zero, we obtain the following governing equation of motion:

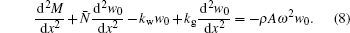
Based on Eringen’ s nonlocal elasticity theory, the nonlocal constitutive equation of EBT nanobeam is given by[23]

where μ = (e0a)2 is the nonlocal parameter and I is the second moment of area. By using Eqs. (8) and (9), M in nonlocal form may be written as

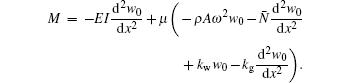
For simplicity and convenience in mathematical formulation, the following non-dimensional parameters have been used:

Equating maximum kinetic and potential energies, one may obtain the following expressions for EBT nanobeams:

2.2. Solution procedure

For applying the R– R method, unknown function W may be written in a series of simple polynomials (Xi− 1, i = 1, 2, … , n) multiplied by a boundary function which ensures that the unknown function satisfies the essential geometric boundary conditions of the beam. The displacement may be expressed as

where N is the number of terms required to compute results, ck are unknowns, and are orthonormal polynomials that are obtained by using the Gram– Schmidt process. The orthogonal polynomials have been generated over the region 0 ≤ X ≤ 1 with the help of a linearly independent set of functions δ k = llk, k = 1, 2, 3, … , N, with l = Xm(1− X)n and lk = Xk− 1. The m takes the values 0, 1, 2 accordingly as the edge X = 0 is free, simply supported, or clamped. The same justification can be given to n for the edge X = 1. The orthonormal polynomials have been generated by the following steps:

where

Here ⟨ ⟩ denotes the inner product of two functions and we define the inner product of two functions, say ϕ i and ϕ k, as

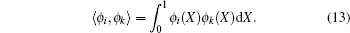
Similarly, the norm of the function ϕ i may be defined as

Then normalized function ϕ i may be obtained by using

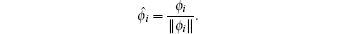
It should be noted that using the boundary characteristic orthogonal polynomial series as the admissible functions has distinct advantages since they are a set of orthogonal series. Therefore, more rapid convergence and better stability in the numerical computation may be achieved.

Free vibration analysis In the case of free vibration, one may obtain the Rayleigh quotient from the following equation of EBT nanobeams:

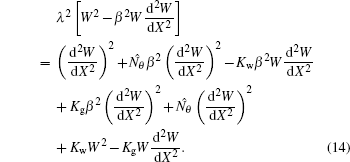
It may be noted here that we have to take N̂ m = 0 in Eq. (10).

Buckling analysis For the buckling analysis, the following eigen equation for EBT nanobeams may be derived from Eq. (14) by setting the inertia term to zero and N̂ m = − P:

where P̂ = PL2/(EI).

Substituting Eq. (11) in Eq. (14) and minimizing λ 2 with respect to the coefficients of the admissible functions that is ∂ λ 2/∂ cj = 0, one may obtain the following eigenvalue value problem:

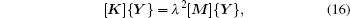
where Y = {c1c2 … cN}T, stiffness matrix K and mass matrix M are given by

Similarly, substituting Eq. (11) in Eq. (15) and minimizing P̂ with respect to the coefficients of the admissible functions, that is ∂ P̂ /∂ cj = 0, the following eigenvalue value problem may be obtained:

where Z = {c1c2 … cN}T, stiffness matrix K and buckling matrix B are given by

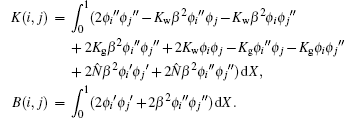
3. Numerical results and discussion

The boundary characteristic orthogonal polynomials as shape functions have been implemented in the Rayleigh– Ritz method to analyze vibration and buckling of single-walled carbon nanotubes embedded in an elastic medium (Fig. 1) under the influence of temperature. The elastic medium is modeled as Winkler-type and Pasternak-type foundations. The present formulation is based on the nonlocal Euler– Bernoulli beam theory. The effective properties of SWCNTs are taken as follows:[29, 33] Young’ s modulus E = 1000 GPa, Poisson’ s ratio ν = 0.19, α x = − 1.6 × 10− 6 for room temperature, and α x = 1.1 × 10− 6 for high temperature. A computer code has been developed by the authors in MATLAB based on Eqs. (16) and (17).

Fig. 1. Single-walled carbon nanotubes embedded within an elastic medium characterized by spring constant Kw and shear constant Kg.

3.1. Convergence

First of all, the convergence pattern has been carried out to compute results. Table 1 shows the convergence of the first three frequency parameters of EBT nanobeams with CC support in a low temperature environment. In this table, we have taken Kw = 50, Kg = 2, θ = 20 K, e0a = 0.5 nm, and L/d = 10. Next, we show the convergence pattern graphically for buckling analysis. Figure 2 illustrates the convergence of critical buckling load parameter P̂ cr. In this figure, we have considered the CS edge condition with L/d = 20, e0a = 1 nm, Kw = 60, Kg = 4, and θ = 10 K. The above convergence patterns show that ten grid points are sufficient to obtain results in the present analysis.

Table 1. Convergence of the first three frequency parameters of CC nanobeams.

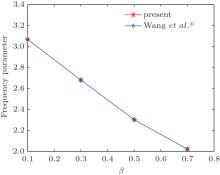
Fig. 2. Convergence of critical buckling load parameter.

3.2. Validation

To validate the present results, a comparison study has been carried out with the results of Wang et al.[21, 22] In their analyses, the frequency and critical buckling load parameters have been given for four sets of boundary conditions. For this comparison, we have taken Kw = 0, Kg = 0, and θ = 0 K. Figures 3 and 4 show the comparison for vibration and buckling analyses, respectively. We have considered SS support with L/d = 10 in Fig. 3 and CS support with L/d = 14 in Fig. 4. Excellent agreement in results is noticed from Figs. 3 and 4. Tabular comparison is shown in Table 22 for cantilever Euler– Bernoulli nanobeams with Ref. [45]. One may observe close agreement of the results with Ref. [45]. This shows the suitability and reliability of the present method for the vibration and buckling analyses of SWCNTs.

Fig. 3. Comparison of fundamental frequency parameter.

Fig. 4. Comparison of critical buckling load parameter.

Table 2. Comparison of cantilever Euler– Bernoulli nanobeams.
3.3. Effect of Winkler modulus parameter

In this subsection, we investigate the influence of the surrounding medium on the vibration and buckling analyses of SWCNTs. The elastic medium is modeled as Winkler-type and Pasternak-type foundations. To show the effect of the Winkler modulus parameter, we consider EBT nanobeams with CS support in a low temperature environment. The various parameters are taken as L/d = 10, Kg = 0, θ = 20 K. Figure 5 shows the effect of the Winkler modulus on the fundamental frequency parameter. In this figure, the results are shown for various scale coefficients (e0a = 0 nm, 0.5 nm, 1 nm, 1.5 nm, 2 nm). The Winkler modulus parameter is taken in the range of 0– 400. It is observed from this figure that the frequency parameter decreases with the increase in the scale coefficient. It may be noted that the results associated with e0a = 0 nm correspond to those of the local beam theory. As the scale coefficient e0a increases, the frequency parameter obtained from the nonlocal beam theory becomes smaller than that from its local counterpart. This is due to the fact that the nonlocal model may be viewed as atoms linked by elastic springs, while the local continuum model assumes the spring constant to take on an infinite value and the small scale effect makes the CNTs more flexible.[21] Therefore, the nonlocal theory should be considered for static and dynamic analyses of structures at nanoscale. It is also seen that the frequency parameter increases with the increase in the Winkler modulus parameter. This is because the nanotube becomes stiffer when the elastic medium constant is increased. This increasing trend of the fundamental frequency parameter with the surrounding elastic medium is influenced significantly by the small scale coefficients. Similarly, to analyze the effect of the Winkler modulus parameter on the buckling solutions, we take EBT nanobeams with CF support in a low temperature environment. The parameters are Kg = 0, θ = 30 K, L/d = 10. Figure 6 shows the variation of the critical buckling load parameter with the Winkler modulus parameter. The scale coefficients are taken as e0a = 0 nm, 0.5 nm, 1 nm, 1.5 nm, 2 nm. Here, the Winkler modulus parameter is also taken in the range of 0– 400. It is seen that the critical buckling load increases with the increase in the Winkler modulus parameter. The cause may be that increasing the elastic medium constant makes the nanotube stiffer.[33] The buckling solutions are also affected by the small scale coefficients. The critical buckling loads are higher for lower scale coefficients. In addition, it is also observed that the critical buckling loads show a nonlinear behavior with respect to the stiffness of the surrounding matrix for higher e0a. This may be due to the fact that the increase of the Winkler modulus causes CNT to be more rigid.

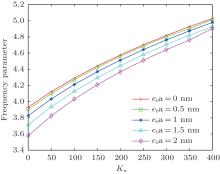Fig. 5. Effect of the Winkler modulus parameter on the frequency parameter for various small-scale coefficients.

Fig. 6. Effect of the Winkler modulus parameter on the critical buckling load parameter for various small-scale coefficients.

3.4. Effect of Pasternak shear modulus parameter

In this subsection, the effect of the Pasternak shear modulus parameter on the vibration and buckling solutions is examined. Figure 7 illustrates the fundamental frequency parameter as a function of the Pasternak shear modulus parameter Kg based on EBT with CC support in a low temperature environment. The parameters are Kw = 0, L/d = 30, and θ = 20 K. The figure is plotted for various scale coefficients with the Pasternak shear modulus parameter ranging from 0 to 10. It is observed from the figure that the frequency parameter associated with the first mode increases with the Pasternak shear modulus parameter. This may be due to the effective stiffness of the elastic medium. With increase in the scale coefficient, the frequency parameter for a particular Pasternak shear modulus parameter decreases. Similarly, figure 8 shows the distribution of the critical buckling load parameter against the Pasternak shear modulus in a low temperature environment. The results are given for the EBT nanobeam with CS support.

Fig. 7. Effect of the shear modulus parameter on frequency parameter for various small-scale coefficients.

Fig. 8. Effect of the shear modulus parameter on critical buckling load parameter for various small-scale coefficients.

The parameters are chosen as Kw = 0, θ = 10 K, L/d = 40. Here, we have also incorporated the results for different scale coefficients. One may observe the same trend as that in the case of vibration. It is also observed that unlike the Winkler foundation model, the increase of the fundamental frequency parameter and the critical buckling load parameter with the Pasternak foundation is linear in nature. This is due to the domination of the elastic medium modeled as the Pasternak type foundation model. The same observation has also been reported in Ref. [33].

3.5. Effect of temperature

The effect of temperature on the vibration of nanobeams embedded in an elastic medium is investigated and shown in Fig. 9. In this graph, we have taken L/d = 10, e0a = 1.5 nm, Kw = 10, Kg = 4. The results are shown for the EBT nanobeams with SS support in both high and low temperature environments. It may be seen that the frequency parameter varies linearly with the temperature change. Similarly, the effect of temperature on the buckling solutions is illustrated in Fig. 10. In this figure, we have taken SS nanobeams with L/d = 20, e0a = 2 nm, Kw = 50, Kg = 2. It is noticed that the frequency and the critical buckling load parameters increase with increase in temperature in a low temperature environment while they decrease with increase in temperature in a high temperature environment. In a high temperature environment, the increase in temperature decreases the stiffness of the nanobeams and hence leads to lower frequency and critical buckling load parameters. Similarly, in a low temperature environment, the increase in temperature increases the stiffness of the nanobeams and hence leads to increased frequency and critical buckling load parameters. Thus, one may say that the frequency and critical buckling load parameters considering the thermal effect are larger than those ignoring the influence of the temperature change in a low temperature environment. Meanwhile, in a high temperature environment, the frequency and buckling load parameters considering the thermal effect are smaller than those excluding the influence of the temperature change. The same observation has also been reported in Refs. [27], [28], [32], and [36].

Fig. 9. Change of the frequency parameter with temperature in both low and high temperature environments.

Fig. 10. Change of the critical buckling load parameter with temperature in both low and high temperature environments.

3.6. Effect of aspect ratio

To illustrate the effect of the aspect ratio on the fundamental frequency parameter, the variation of the scale load ratio (χ scale) with the aspect ratio (L/d) is shown in Fig. 11 for different temperature changes. It may be noted that the scale load ratio is defined as χ scale = frequency parameter calculated using nonlocal theory/frequency parameter calculated using local theory. It is observed that scale load ratio increases with increase in the aspect ratio. In addition, it is also seen that the frequency parameter is also dependent on the temperature change θ . The differences in the frequency parameter for different temperature changes are larger at low aspect ratios, while they are smaller at large aspect ratios. It is also seen that for larger temperature changes, the rate of the increase of the scale load ratio is smaller compared to that for smaller temperature changes. It may be noted that the same trend is also seen in the case of buckling.

Fig. 11. Change of the scale-based frequency ratio with aspect ratio for different changes in temperature.

4. Conclusion

Boundary characteristic orthogonal polynomials as shape functions have been applied in the Rayleigh– Ritz method to investigate the thermal effect on the vibration and buckling of nanobeams embedded in an elastic medium. Four sets of boundary conditions have been taken into consideration. Theoretical formulations include effects of small scale, elastic medium, and temperature change. It is noted that the use of boundary characteristic orthogonal polynomials in the R– R method requires less computational effort because of the orthogonal property. It is seen that the results obtained based on the local beam theory are overestimated. The frequency and critical buckling load parameters increase with increase in temperature, Winkler type foundation, and Pasternak type foundation. It is also observed in the case of room or low temperature, the results obtained including the thermal effect are larger than those ignoring the influence of temperature, whereas in the case of high temperature, the results obtained with the thermal effect are smaller than those excluding the thermal effect.

Reference
1 Tan Y and Wang Y G 2013 Chin. Phys. Lett. 30 117901 DOI:10.1088/0256-307X/30/11/117901 [Cited within:1]
2 Tan Y and Wang Y G 2013 Chin. Phys. Lett. 30 047901 DOI:10.1088/0256-307X/30/4/047901 [Cited within:1]
3 Tan Y and Wang Y G 2013 Chin. Phys. Lett. 30 017902 DOI:10.1088/0256-307X/30/1/017902 [Cited within:1]
4 Tan Y and Wang Y G 2013 Chin. Phys. Lett. 30 017901 DOI:10.1088/0256-307X/30/1/017901 [Cited within:1]
5 Wang W H, Wang W Z and Xu H X 2011 Chin. Phys. Lett. 28 078103 DOI:10.1088/0256-307X/28/7/078103 [Cited within:1]
6 Jia W L, Zhao L, Hou L, Ji W L, Shi W and Qu G H 2014 Acta Phys. Sin. 63 077201 DOI:10.7498/aps.63.077201(in Chinese) [Cited within:1]
7 Wang Y L, Su K H, Yan H X and Wang X 2014 Acta Phys. Sin. 63 046101 DOI:10.1038/aps.2014.52(in Chinese) [Cited within:1]
8 Lei D, Menggen Q Q G, Zhang H L and Zhi Y B 2013 Acta Phys. Sin. 62 248502 DOI:10.7498/aps.62.248502(in Chinese) [Cited within:1]
9 Li M Y, Yu M, Su Q, Liu X Q, Xie E Q and Zhang X Q 2012 Acta Phys. Sin. 61 236101(in Chinese) DOI:10.7498/aps.61.236101 [Cited within:1]
10 Wang Y L, Su K H, Wang X and Liu Y 2011 Acta Phys. Sin. 60 098111(in Chinese) [Cited within:1]
11 Shao Z F, Yang Y Q, Liu S T and Wang Q 2014 Chin. Phys. B 23 096105 DOI:10.1088/1674-1056/23/9/096105 [Cited within:1]
12 Shao Z F, Yang Y Q, Liu S T and Wang Q 2014 Chin. Phys. B 23 096102 DOI:10.1088/1674-1056/23/9/096102 [Cited within:1]
13 He C X, Jian Y, Qi X Y and Xue J K 2014 Chin. Phys. B 23 025202 DOI:10.1088/1674-1056/23/2/025202 [Cited within:1]
14 Han Z D, Li X Y, Yang Z, Liu R P, Liu S D and Zhang Y 2012 Chin. Phys. B 21 118102 DOI:10.1088/1674-1056/21/11/118102 [Cited within:1]
15 Ren Y, Ma W J, Zeng Q S, Li J Z, Dong H B and Zhou We Y 2012 Chin. Phys. B 21 098103 DOI:10.1088/1674-1056/21/9/098103 [Cited within:1]
16 Iijima S 1991 Nature 354 56 DOI:10.1038/354056a0 [Cited within:1]
17 Ruud J A, Jervis T R and Spaepan F 1994 J. Appl. Phys. 75 4969 DOI:10.1063/1.355787 [Cited within:1]
18 Eringen A C 1972 International Journal of Engineering Science 10 1 DOI:10.1016/0020-7225(72)90070-5 [Cited within:2]
19 Peddieson J, Buchanan G R and McNitt R P 2003 International Journal of Engineering Science 41 305 DOI:10.1016/S0020-7225(02)00210-0 [Cited within:1]
20 Xu M 2006 Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science 462 2977 DOI:10.1098/rspa.2006.1712 [Cited within:1]
21 Wang C M, Zhang Y Y and He X Q 2007 Nanotechnology 18 105401 DOI:10.1088/0957-4484/18/10/105401 [Cited within:3]
22 Wang C, Zhang Y, Ramesh S S and Kitipornchai S 2006 J. Phys. D: Appl. Phys. 39 3904 DOI:10.1088/0022-3727/39/17/029 [Cited within:1]
23 Reddy J 2007 International Journal of Engineering Science 45 288 DOI:10.1016/j.ijengsci.2007.04.004 [Cited within:1]
24 Aydogdu M 2009 Physica E 41 1651 DOI:10.1016/j.physe.2009.05.014 [Cited within:1]
25 Ghannadpour S, Mohammadi B and Fazilati J 2013 Composite Structures 96 584 DOI:10.1016/j.compstruct.2012.08.024 [Cited within:1]
26 Ansari R, Sahmani S and Rouhi H 2011 a Phys. Lett. A 375 1255 DOI:10.1016/j.physleta.2011.01.046 [Cited within:1]
27 Maachou M, Zidour M, Baghdadi H, Ziane N and Tounsi A 2011 Solid State Commun. 151 1467 DOI:10.1016/j.ssc.2011.06.038 DOI:10.1016/j.physleta.2011.01.046 [Cited within:3]
28 Zidour M, Benrahou K H, Semmah A, Naceri M, Belhadj H A, Bakhti K and Tounsi A 2012 Computational Materials Science 51 252 DOI:10.1016/j.commatsci.2011.07.021 [Cited within:2]
29 Benzair A, Tounsi A, Besseghier A, Heireche H, Moulay N and Boumia L 2008 J. Phys. D: Appl. Phys. 41 225404 DOI:10.1088/0022-3727/41/22/225404 [Cited within:2]
30 Wang L, Ni Q, Li M and Qian Q 2008 Physica E 40 3179 DOI:10.1016/j.physe.2008.05.009 [Cited within:1]
31 Zhang Y, Liu X and Liu G 2007 Nanotechnology 18 445701 DOI:10.1088/0957-4484/18/44/445701 [Cited within:1]
32 Murmu T and Pradhan S 2009 Computational Materials Science 46 854 DOI:10.1016/j.commatsci.2009.04.019 [Cited within:2]
33 Murmu T and Pradhan S 2009 Physica E 41 1232 DOI:10.1016/j.physe.2009.02.004 [Cited within:4]
34 Narendar S and Gopalakrishnan S 2011 Physica E 43 1185 DOI:10.1016/j.physe.2011.01.026 [Cited within:1]
35 Ansari R, Gholami R and Darabi M 2011 Journal of Thermal Stresses 34 1271 DOI:10.1080/01495739.2011.616802 [Cited within:1]
36 Murmu T and Pradhan S 2010 Computational Materials Science 47 721 DOI:10.1016/j.commatsci.2009.10.015 [Cited within:2]
37 Tounsi A, Semmah A and Bousahla A A 2013 Journal of Nanomechanics and Micromechanics 3 37 DOI:10.1061/(ASCE)NM.2153-5477.0000057 [Cited within:1]
38 Bhat R 1991 Journal of Sound and Vibration 149 170 DOI:10.1016/0022-460X(91)90923-8 [Cited within:1]
39 Singh B and Chakraverty S 1992 Journal of Sound and Vibration 152 149 DOI:10.1016/0022-460X(92)90071-5 [Cited within:1]
40 Singh B and Chakraverty S 1994 Communications in Numerical Methods in Engineering 10 1027 DOI:10.1002/cnm.1640101209 [Cited within:1]
41 Singh B and Chakraverty S 1994 Journal of Sound and Vibration 173 157 DOI:10.1006/jsvi.1994.1224 [Cited within:1]
42 Singh B and Chakraverty S 1994 c Journal of Sound and Vibration 173 289 DOI:10.1006/jsvi.1994.1231 [Cited within:1]
43 Behera L and Chakraverty S 2014 Meccanica 49 51 DOI:10.1007/s11012-013-9771-2 [Cited within:1]
44 Amirian B, Hosseini-Ara R and Moosavi H 2012 Archives of Mechanics 64 581 [Cited within:1]
45 Li M and Zheng H 2013 Research Journal of Applied Sciences Engineering and Technology 5 2729 [Cited within:2]