Recently, zinc oxide (ZnO) semiconductors have attracted much interest because of their potential applications in optoelectronic devices in the blue– ultraviolet wavelength region.^{[1– 5]} ZnO has some advantages over GaN, among which are the availability of fairly high-quality ZnO bulk single crystals and its high exciton binding energy (60 meV). ZnO-based quantum well (QW) structures also have several advantages over GaN-based QW structures, ^{[6– 8]} including the much lower growth temperature of ZnO than that of GaN. Wurtzite ZnO exhibits mixing of the longitudinal optical (LO) and transverse optical (TO) modes because of its anisotropy.^[9] As material synthesis has improved, the production of ZnO-based semiconductor alloys has led to high-quality ZnO/Mg_xZn_{1− x}O multiple-QW structures.^{[8, 10– 12]} In recent years, researchers have studied the luminescent properties, absorption spectra, lattice vibrations, and exciton states of ZnO/Mg_xZn_{1− x}O QWs.^{[6, 10, 13– 25]} For example, Coli et al. investigated the excitonic transition energies in these heterostructures, accounting for the effects of the exciton– phonon interaction.^[13] Fan et al. calculated the band parameters and electronic structures of wurtzite ZnO and ZnO/Mg_xZn_{1− x}O QWs by the empirical pseudopotential method.^[14] Chia et al. studied how the well width affected radiative and nonradiative recombination times in ZnO/MgZnO multiple QWs.^[15] Fan et al. studied the band offsets and polarization effects in wurtzite ZnO/Mg_0.25Zn_0.75O QWs.^[17]

Using the dielectric continuum model and Loudon’ s uniaxial crystal model, Lee et al. deduced the dispersion relation of the interface (IF) phonon modes, the confined (CF) phonon modes, the half-space (HS) phonon modes, and the propagating (PR) phonon modes in wurtzite quantum structures with single and double heterointerfaces.^[26] Shi et al. exactly solved the equation of motion for the p-polarization field in an arbitrary wurtzite multilayer heterostructure by using a transfer matrix method, and also obtained and discussed the dispersive relation and electron– phonon coupling functions.^{[27, 28]}

Polarons influence carrier transport in semiconductors, which in turn influence the properties of optical– electronic devices, so it is important to understand the polaronic effects in wurtzite ZnO-based QWs. In a previous work, we calculated the binding energy of a bound polaron in ZnO/Mg_xZn_{1− x}O QWs.^[29] However, many of the fundamental electronic and optical properties of ZnO-based QW structures are not yet well understood. To the best of our knowledge, there is no detailed theoretical calculation for the polaronic effects in ZnO/Mg_xZn_{1− x}O QW structures.

The present paper focuses on the polaronic effect and the contributions from various phonon modes to the ground state energy and transition energy in wurtzite ZnO/Mg_xZn_{1− x}O QWs by considering the influence of CF phonon modes, HS phonon modes, IF phonon modes (including the LO-like and the TO-like modes), as well as the anisotropy of the electron effective band mass, phonon frequency, and dielectric constant.

In this work, we consider a wurtzite ZnO/Mg_xZn_{1− x}O QWs structure of polar dielectrics for which the well material is in the region λ = 1, | z| < d/2, and the barriers are in the region λ = 2, | z| ≥ d/2. By using the effective-mass approximation and considering the anisotropy of material parameters, the Hamiltonian of the electron– phonon system including the interactions from the CF, IF, and HS phonons can be written as

where m_{λ z} and m_{⊥ λ} are the material-dependent effective mass of the electron with λ = 1, 2, and a_j(w) are the creation and annihilation operators of LO-like and TO-like phonons with wave vector w(w = (q, k_{λ z}) for CF and HS phonon modes, and w = q for IF phonon modes), parity p and frequency ω . j = {p, n}, the mode index p indicates the symmetric and antisymmetric phonon modes, n indicates the CF, HS, and IF modes in LO-lik and TO-lik phonon frequency regions, V(z) is the rectangular well potential experienced by the electron and is given as

where V₀ = 0.65 × Δ E_g = 844  meV^[2] is the depth of the QWs.

The last term in Eq.  (1) is the Hamiltonian of the interaction between electron and phonon, ^[26] and is given by

For the symmetric localized modes, the coupling function g_j(z) in Eq.  (3) is determined by the following equation:^[26]

where , k_1m can be determined by the following equation: ε _1zk_1m sin(k_1md/2) − ε _2zk₂ cos(k_1md/2) = 0, and the range of k_1m is 2mπ /d < k_1m < 2(m + 1)π /d, m runs over the series of confined modes, and S is the interface area of quantum well.

For the antisymmetric localized modes, the coupling function in Eq.  (3) is determined by the following equation:^[26]

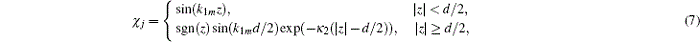
where

where k_1m can be determined by ε _1zk_1m cos(k_1md/2) + ε _2zk₂ sin(k_1md/2) = 0, and the range of k_1m is 2(m − 0.5)π /d < k_1m < 2(m + 0.5)π /d.

Similar to the CF modes, the HS and IF modes can be found in Ref.  [26]. The phonon frequencies ω for CF (HS) modes are obtained from ε _{λ ⊥} sin²θ _λ + ε _{λ z} cos²θ _λ = 0 with a proper application of parameters for material 1 (2), θ _λ is an angle between w and the z axis. The direction-dependent dielectric functions, ε _{λ ⊥} and ε _{λ z} are functions of ω , and are given in Ref.  [26]. The frequency ω for symmetric IF modes is determined by with ε _1zε _2z < 0 (ε _1⊥ ε _1z > 0 and ε _2⊥ ε _2z > 0), and the frequency ω for antisymmetric IF modes is determined by with ε _1zε _2z < 0.

The Hamiltonian in Eq.  (1) is too complicated to be solved exactly. We now perform two unitary transformations with

the transformed Hamiltonian is given by

Here, the displacement amplitudes f_j and are variational parameters which will be determined by minimizing the energies of the electron– phonon system. The wave function of the polaron can be expressed in the form

where N_n is the normalization constant, | 0〉 is the zero-phonon state of the phonon field, and φ _n(z) is the wave function in the z direction. The polaronic energy can then be written as

For the ground state,

and the wave function of the first excited state is given as follows:

In Eqs.  (13) and (14), and . Here, is the sub-band energy of an electron in the QWs.

By substituting Eqs.  (11), (13), and (14) into Eq.  (12), one can obtain the ground state energy (E₁) and the first excited state energy (E₂) of the polaron. The transition energy from the ground state to the first excited state can be given by

To clarify the influence of the polaronic effect caused by the full optical phonon modes (CF, HS, and IF) in the wurtzite QW system, we numerically calculated the energy levels of the ground and the excited states of a polaron in wurtzite ZnO/Mg_xZn_{1− x}O QWs. Table  1 lists the parameters used in the calculation, and figures  1– 5 give the calculated results. The parameters of the barrier material (Mg_xZn_{1− x}O) were obtained by the effective phonon-mode approximation: Q^{M_gxZn_{1− x}O} = (1 − x)Q^ZnO + xQ^MgO.

Table 1.

Table 1.

Table 1. The parameters for wurtzite QWs used in the calculation. The electron effective masses, phonon frequency, and band gap have units of electron rest mass me, meV, and eV, respectively. Materials m⊥ mz ω ⊥ ω z ω ⊥ L ω zL Eg ZnO 0.21[30] 0.23[30] 3.70[31] 3.78[31] 50.71[31] 47.11[31] 72.78[31] 71.17[31] 3.37 [32] MgO 0.28[33] 0.28[33] 2.60[34] 2.60[34] 49.72[35] 49.72[35] 89.15[35] 89.15[35] 7.7[36]

Table 1. The parameters for wurtzite QWs used in the calculation. The electron effective masses, phonon frequency, and band gap have units of electron rest mass me, meV, and eV, respectively.

Figure  1 shows the ground state energies of the polaron (E₁) as a function of well width d in the wurtzite ZnO/Mg_0.3Zn_0.7O QW with and without phonons effect. To understand the influence of the phonons on the transition energy, we also propose the results of the transition energies, considering the presence of phonons. Figure  1 shows that the ground state energies of the polaron in both cases (with and without the influence of phonons) follow the same trend. Both decrease monotonically with increasing d, rapidly at smaller d but slowly at larger d. This behavior occurs because the polarons are more strongly confined when d is small. The contribution of the electron– optical phonon interaction to the ground state energy of the polaron in a ZnO/Mg_0.3Zn_0.7O QW (∼ 67– 86  meV) is much larger than in a GaAs/Al_0.3Ga_0.7As QW (∼ 1.8– 3.2  meV). Note that the ground state energy with phonon influence is smaller than that without phonon influence in the wurtzite ZnO/Mg_0.3Zn_0.7O QW. For example, for d = 8  nm, the ground state energy of the polaron is − 49.73 (20.82)  meV including (ignoring) the phonon effect. For d = 20  nm, the corresponding ground state energy of the polaron is − 65.26 (4.60)  meV. This difference demonstrates the significant influence of the phonons on the ground state energy of the polaron. Moreover, the effect becomes more obvious as the quantum well width d decreases. The transition energy decreases as the well width increases. The results of the transition energy can be compared to the experiment results, so we urge an experimental observation of these properties in wurtzite ZnO/Mg_0.3Zn_0.7O QW.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. The ground energies and the transition energies of the polaron in wurtzite ZnO/Mg0.3Zn0.7O QWs as functions of the well width d. The short dash line is the results of the transition energy with phonons.

In Fig.  2, we calculate the contributions of different phonons (CF, IF, HS modes) to the ground state energies of the polaron in wurtzite ZnO/Mg_0.3Zn_0.7O QWs as functions of the well width d. To understand the total contribution from the three phonon modes, we also present it in Fig.  2(a) with the symbol line. Figure  2(a) shows that the total phonon contributions are remarkable, which have a larger negative contribution to the polaron ground state energy, and it decreases gradually with increasing well width. Figure  2(a) also shows that, when d is narrow, the CF modes contribute little to the polaronic ground state energy. As the well width increases, the contributions come from symmetric, antisymmetric, and their summation CF phonon modes to E₁ increase rapidly at first but slowly increase later. This behavior occurs because, as the well width increases, the tunneling effect of the electron wave function gradually weakens and becomes a nearly free electron. At the same time, the increase in coupling between electrons and confined phonons strengthens the electron– CF phonon interaction, so it dominates the contribution to E₁. At larger d, the interaction between electrons and CF phonon modes increases, making it more important to the contribution to E₁. Furthermore, the contribution of the symmetric CF phonon mode is larger than that of the antisymmetric CF phonon mode.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Contributions of phonons to the ground energies of the polarons in wurtzite ZnO/ MgxZn1− xO QWs as functions of the well width d. The contribution Δ Ee− ph separately contributed from the CF, IF, and HS phonon modes are shown in panels (a), (b), and (c). The symbol line is the total contribution from the different phonon modes in panel (a).

Figures  2(b) and 2(c) show the contributions from the IF and HS phonon modes, revealing that, when d is very small, the main contribution to the polaron ground state energies comes from the HS modes and IF modes. As d increases, the negative contributions from the IF modes decrease smoothly. This behavior occurs because the electron– IF-phonon coupling intensity decreases gradually as d increases, decreasing the contribution to polaronic ground state energies. Figure  2(b) also shows that the contribution of the symmetric IF phonon mode is larger than that of the antisymmetric IF phonon mode. As shown in Fig.  2(c), as d decreases, the negative contribution of the HS phonon mode (including symmetric and antisymmetric) to E₁ decreases markedly. As d increases, the contribution decreases gradually. When d is sufficiently large, the contribution of the HS phonon mode to E₁ approaches 0. This behavior occurs because the electronic localization strengthens as d increases, decreasing the coupling intensity between the electrons and HS phonons.

Figure  3 shows the contributions of the different phonon modes to the transition energy of the polaron with different QW widths. The contribution to the transition energy is defined as Δ E_{e− ph} = Δ E_{e− ph} (excited state)– Δ E_{e− ph} (ground state). This figure reveals that the total contribution of the phonon modes to the transition energy is negative and increases gradually with the QW width d. This is a comprehensive result of the contributions from the various phonon modes. The contributions of the various phonon modes to the transition energy change differently with increasing well width. The contribution of the CF phonons is positive, but the contribution of the IF and HS phonons is negative. Furthermore, the contribution of the HS phonons decreases slowly with QW width, whereas the contribution of the IF phonons maximizes at d ≈ 5  nm and then decreases slowly. The contribution of the CF phonons increases as d increases, quickly reaching a maximum at d ≈ 7  nm before decreasing gradually. This behavior can be explained physically as follow. With a fixed well width, the probability of an excited-state electron to tunnel through a barrier is greater than that of a ground-state electron. Thus, electrons interact with CF (HS, IF) phonons less (more) in the excited state than in the ground state.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Contributions of phonons to the transition energies of the polaron in wurtzite ZnO/ Mg0.3Zn0.7O QWs as functions of the well width d.

In Fig.  4, we further calculate the contributions of various phonon modes to the ground state energies of the polaron in wurtzite ZnO/Mg_xZn_{1− x}O QWs as functions of the composition x. Figure  4(a) shows that, as the composition x increases, the total contribution of phonons to the ground state energy increases nearly linearly. This is a comprehensive result of the contributions from the various phonon modes. Figure  4(a) also demonstrates that, as x increases, the contribution of CF phonons increases very smoothly. This behavior occurs because the coupling between the electrons and CF phonons strengthens as x increases. Both the symmetric and antisymmetric CF phonon modes follow the same trend. As shown in Fig.  4(b), as x increases, the contribution of the symmetric IF phonons to the ground state energy increases while the contribution of the antisymmetric IF phonons decreases. The total contribution still increases with x because the symmetric IF phonons contribute more than the antisymmetric phonons. Figure  4(c) shows that the contribution of the HS phonons decreases as x increases. This behavior occurs because the coupling between the electrons and HS phonons weakens with increasing x. As a result, x plays an important role in determining how the phonons contribute to the ground state energy.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Contributions of phonons to the ground state energies of the polaron in wurtzite ZnO/ MgxZn1− xO QWs as functions of the composition x for given d = 12  nm. The contribution Δ Ee− ph separately contributed from the CF, IF, and HS phonon modes are shown in panels (a), (b), and (c). The symbol line is the total contribution from the different phonon modes.

Figure  5 shows the contributions of phonons to the transition energies of the polaron in wurtzite ZnO/Mg_xZn_{1− x}O QWs as functions of the composition x. As the composition x increases, the contributions of various phonons decrease gradually. This behavior occurs because the quantum confinement of an electron strengthens as x increases. The tunneling probability of the electron to the barrier decreases, which slowly decreases the contributions of phonons to the transition energies.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Contributions of phonons to the transition energies of the polaron in wurtzite ZnO/ MgxZn1− xO QWs as functions of the composition x.

Our results also show that the contributions induced by the LO-like confined, interface, and half-space phonon modes to the ground state energy of the polaron are approximately two orders of magnitude larger than that induced by the TO-like phonons; thus, the latter contribution can be ignored. Our calculation does not account for the propagating phonons because LO-like propagating phonons do not exist in ZnO/Mg_xZn_{1− x}O QWs because of the condition of ε _1⊥ ε _1z < 0.^[26]

We variationally calculated the phonon contributions from various optical– phonon modes to the ground state and transition energies as functions of the well width and Mg composition, considering the influence of confined optical phonon modes, interface-optical phonon modes, half-space phonon modes, as well as the anisotropy of the electron effective band mass, dielectric constant, and phonon frequency. Our main conclusions are summarized as follows.