Cite this Article
Duan Jie, Zhou Tong, Zhang Li†, Du Ji-Guang, Jiang Gang, Wang Hong-Bin. Elastic properties and electronic structures of lanthanide hexaborides. Chinese Physics B, 24(9): 096201  
Permissions
Elastic properties and electronic structures of lanthanide hexaborides
Duan Jiea), Zhou Tonga), Zhang Li†a), Du Ji-Guangb), Jiang Ganga), Wang Hong-Bina)
Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
College of Physical Science and Technology, Sichuan University, Chengdu 610065, China

†Corresponding author. E-mail: lizhang@scu.edu.cn

Abstract

The structural, elastic, and electronic properties of a series of lanthanide hexaborides ( LnB6) have been investigated by performing ab initio calculations based on the density functional theory using the Vienna ab initio simulation package. The calculated lattice and elastic constants of LnB6 are in good agreement with the available experimental data and other theoretical results. The polycrystalline Young’s modulus, shear modulus, the ratio of bulk to shear modulus B/G, Poisson’s ratios, Zener anisotropy factors, as well as the Debye temperature are calculated, and all of the properties display some regularity with increasing atomic number of lanthanide atoms, whereas anomalies are observed for EuB6 and YbB6. In addition, detailed electronic structure calculations are carried out to shed light on the peculiar elastic properties of LnB6. The total density of states demonstrates the existence of a pseudogap and indicates lower structure stability of EuB6 and YbB6 compared with others.

PACS: 62.20.D–; 71.15.–m; 31.15.A–; 05.70.–a
Keyword: elastic properties; electronic structure; ab initio calculations; thermodynamic properties
1. Introduction

Lanthanide hexaborides (LnB6: Ln = La, Ce, Pr, Nd, Pm, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) have attracted extensive experimental and theoretical interest due to their intriguing physical properties. For example, LaB6 is a typical metal and becomes superconducting at TC = 0.45 K, [1, 2] CeB6 is a dense Kondo material and shows heavy fermion behavior.[3] SmB6, a typical mixed valence compound, has been theoretically proven to be a topological Kondo insulator, which is supported by recent photo emission and transport experiments.[4, 5] YbB6 is found to be a moderately correlated Z2 topological insulator, similar to SmB6 but having a much larger bulk band gap.[6] Furthermore, the lanthanide hexaborides are also considered as hard and refractory materials because of their special cage structure.[7] Bulk lanthanide hexaborides have low work functions ranging from 2.1 eV to 3.8 eV, which make them excellent candidate materials for electron emitter devices.[8] Moreover, they have been applied as scratch-resistant surface decorative coatings due to their tunable attractive colors. For instance, the stoichiometric LaB6 is usually purple, while its color turns to deep blue when it is lanthanum deficient. Consequently, the investigation of the basis physical properties of a series of lanthanide hexaborides such as structural, elastic, and electronic properties is necessary and offers credible references for their various applications.

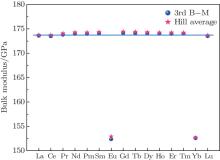
In general, the elastic properties of a solid are important because some physical properties, such as the bulk modulus, shear modulus, Young’ s modulus, and Poisson’ s ratio can be derived from the elastic constants.[9] Up to now, most studies have focused on the magnetic and thermodynamic properties of LnB6.[10] The structural and elastic properties of some LnB6 have also been investigated experimentally by several groups but their results are relatively contradictory or insufficient. Some significantly different values have been reported for the measured elastic constants of CeB6, especially C12; Takegahara et al.[11] gave C12 = − 93 GPa while Nakamura et al.[12] reported a value of 53 GPa for the same constant. The bulk moduli also show small differences among the various experimental reports.[13] On the other hand, single crystal elastic constants for the LnB6 compounds are scarce due to the difficulties of the experiments. The elastic properties of a solid are also closely associated with various fundamental solid-state properties, such as phonon spectra, specific heat, Debye temperature, etc. In view of this, it is necessary and essential to obtain their elastic constants by the first-principles calculations.

As we all know, in the lanthanide series both Eu and Yb are divalent in the solid state while all of the others are in the trivalent state. There is a substantial energy penalty for Eu and Yb to be in the trivalent state. Consequently, systematics are observed for the trivalent Ln and their compounds in terms of crystal structures and physical properties, whereas anomalies are observed for Eu and Yb.[14] The abnormalities relating to Eu and Yb are probably due to their special electronic configurations. Eu has a half-filled 4f orbital and Yb has a completely filled 4f orbital; therefore, they have stable configurations of low energy. But their compounds disturb the stable electronic configurations through charge transfer or chemical bonding. The deviations will be seen repeatedly throughout this work.

The main objective of this paper is to study the regularity of elastic properties and electronic structure of the LnB6 compounds. This paper is organized as follows. The computational methodologies employed in the current study are given in Section 2. We present and discuss the results obtained and compare them with the available experimental and theoretical data in Section 3. Finally, the results are summarized in Section 4.

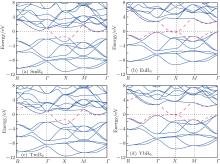
2. Theoretical and computational methods

Our first-principles electronic structure calculations are based on the density functional theory (DFT) in conjunction with projector augmented wave potentials (PAW)[15, 16] within the generalized gradient approximations (GGA) of Perdew– Burke– Ernzerhof (PBE) as implemented in the Vienna ab initio simulation package (VASP).[17– 20] Generally, the PAW potentials are more reliable than the ultra-soft pseudopotentials because of the smaller cut off radius and the more accurate valence electron wave functions in the nuclear area. The validity for the LnB6 binary compounds has been widely verified.[12] Two choices of potentials are available for each Ln element: a standard version in which the entire set of f levels are treated within the valence band and a divalent or trivalent version (e.g., Yb2+ for Yb and Pm3+ for Pm) in which some f electrons are kept frozen in the core. There are several exceptions: (i) there is only a standard potential available for La because it has no occupied f levels in its elemental state, and (ii) there is only a trivalent version of potential available for Tb, Dy, Ho, and Er with VASP. Furthermore, the previous studies of the ground state structures, formation energies, and elastic constants of the Ln elements and compounds[21] indicate that the f core approach is the correct method to treat the Ln elements when thermodynamic and elastic properties are of interest. In this work, pseudopotentials with the f electrons frozen in the core were used throughout. A plane-wave energy cutoff of 550 eV was taken for all LnB6. The 13× 13× 13 k-points for LnB6 unit cell with the Monkhorst– Pack scheme were adopted for the Brillouin zone sampling. In all cases, the total energy of self-consistent convergence was 10− 5 eV/cell and the process was terminated when the atomic force was less than 10− 3 eV/Å . Spin polarization with ferromagnetic ordering was used in all calculations and we found that all the LnB6 considered here are not magnetic. To produce more accurate densities of states, a dense k-point mesh of 19 × 19 × 19 was used, and the total DOS was computed by the Gaussian smearing method.[17– 20] The chosen plane-wave cut off and numbers of k points have been tested carefully to ensure good converged results for all of the computations. The elastic constants were calculated through the energy strain method. The analysis of the density of states indicated the existence of a pseudogap.

3. Results and discussion
3.1. Structural stability and ground state properties

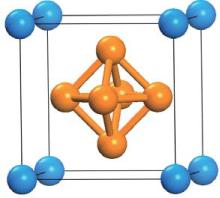
As illustrated in Fig. 1, the lanthanide hexaborides crystallize in cubic CsCl-type structure which belongs to the space group 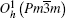.[13] The lanthanide atom is located at the 1a (0, 0, 0) Wyckoff position while the octahedral boron molecule B6 is placed in the 6f Wyckoff position with relative coordinate (1/2, 1/2, x), where x is the positional parameter. The primitive unit cell contains seven atoms. The equilibrium lattice parameter a0 has been computed by minimizing the crystal total energy by means of Murnaghan’ s equation of state (EOS).[22] Our calculated lattice parameter a0 and internal position x along with related experimental and theoretical values are listed in Table 1. In our GGA calculations, the predicted lattice constant of LaB6 is 4.1558 Å , which is in good agreement with the experimental data 4.1565 Å [10] and other theoretical results 4.1300 Å , [10] 4.1277 Å , [10] 4.1560 Å .[23] For CeB6, the present optimized lattice parameter a0 is 4.1585 Å in accordance with the experimental data 4.1410 Å .[23] For other LnB6, the results obtained are also comparable to their experimental values in Table 1, with a difference within 3%. This elucidates that the present calculations are reasonable and reliable. The LnB6 compounds tend to decrease in size as going down the lanthanide series as shown in Fig. 2. We refer to this effect as the lanthanide contraction. While we note that Eu- and Yb-containing systems do not follow the trends of the rest of the lanthanides. There is not enough data to compare with our results of the positional parameters x but the changes can be neglected, and they are all approximately equal to 0.2 Å . The positional parameters x of EuB6 and YbB6 are larger than those of the others and closer to the “ equal distance” of 0.2070 Å .[31] The abnormal behaviors of Eu and Yb are probably due to their special electronic configurations.

Fig. 1. Unit cell of lanthanide hexaboride (LnB6).

Fig. 2. The change of lattice parameter a0 with the atomic number of Ln atoms in LnB6.

Table 1. Calculated lattice parameters a0, positional parameter of boron atoms x, bulk modulus B0, equilibrium volume V, pressure derivative , and independent elastic constants C11, C12, C44 for LnB6 accompanied with other calculated and experimental results.
3.2. Elastic properties</span><p>The most common assessment of mechanical properties can be made by the determination of the elastic constants. The elastic properties present valuable information about the mechanical and dynamical properties of crystals, the forces operating in solids, and they also provide important data for developing the interatomic potentials.<sup>[<span class="xref"><a href="#cpb150207bib32">32</a></span>, <span class="xref"><a href="#cpb150207bib33">33</a></span>]</sup> The elastic constants are identified as proportional to the second order coefficient in a polynomial and they can be derived from the energy variation by applying small strains to the equilibrium lattice configuration.<sup>[<span class="xref"><a href="#cpb150207bib34">34</a></span>]</sup> For the cubic structure, the independent elastic constants are <em>C</em><sub>11</sub>, <em>C</em><sub>12</sub>, and <em>C</em><sub>44</sub>, <sup>[<span class="xref"><a href="#cpb150207bib31">31</a></span>]</sup> which can be calculated through the following sets of strains: (i) <em>ε </em><sub>11</sub> = <em>ε </em><sub>12</sub> = <em>δ </em>; (ii) <em>ε </em><sub>11</sub> = <em>ε </em><sub>22</sub> = <em>ε </em><sub>33</sub> = <em>δ </em>; and, (iii) <em>ε </em><sub>12</sub> = <em>ε </em><sub>21</sub> = <em>ε </em><sub>13</sub> = <em>ε </em><sub>31</sub> = <em>ε </em><sub>23</sub> = <em>ε </em><sub>32</sub> = <em>δ </em>/2. In the present work, we have calculated 15 sets of Δ <em>E</em>/<em>V</em> ∼ <em>δ </em> by varying <em>δ </em> from − 0.014 to 0.014 in steps of 0.002. The results are listed in <a anchor="table">Table 1.</a> As a comparison, the previous theoretical result and the available experimental data are also presented in <a anchor="table">Table 1.</a> The published data on the elastic properties of hexaborides are scarce for most compounds, while there are ample experimental and theoretical results for LaB<sub>6</sub> and CeB<sub>6</sub>. For <em>C</em><sub>11</sub> and <em>C</em><sub>44</sub>, our results are in excellent agreement with others, while for <em>C</em><sub>12</sub> the experimental and theoretical results given in the table demonstrate a large discrepancy among themselves. The origin of the large errors for <em>C</em><sub>12</sub> can be understood because <em>C</em><sub>11</sub> and <em>C</em><sub>12</sub> are determined using associated methods for both theoretical calculations and experiments. As <em>C</em><sub>11</sub> is considerably larger than <em>C</em><sub>12</sub>, the large numerical error is consequently hard to avoid in the determination of <em>C</em><sub>12</sub>.<sup>[<span class="xref"><a href="#cpb150207bib34">34</a></span>]</sup> Obviously, the agreement between experiments and our calculations affirms the feasibility of our calculation scheme. The mechanical stability criterion<sup>[<span class="xref"><a href="#cpb150207bib35">35</a></span>]</sup> of the cubic lattice for elastic is (<em>C</em><sub>11</sub>− <em>C</em><sub>12</sub>) > 0, <em>C</em><sub>11</sub> > 0, <em>C</em><sub>44</sub> > 0, and (<em>C</em><sub>11</sub> + 2<em>C</em><sub>12</sub>) > 0. As illustrated in <a anchor="table">Table 1, </a> the elastic constants meet the criterion mentioned above, which indicates that all of the <em>Ln</em>B<sub>6</sub> are mechanically stable under zero pressure.</p><p>Since the elastic constants actually refer to a single crystal at microscopic scale and are normally not representative of the mechanical properties at larger length scales in actual applications, we turn to estimate the macroscopic parameters such as the shear modulus <em>G</em> and the bulk modulus <em>B</em>.<sup>[<span class="xref"><a href="#cpb150207bib36">36</a></span>]</sup> The Voigt– Reuss– Hill (VRH)<sup>[<span class="xref"><a href="#cpb150207bib37">37</a></span>– <span class="xref"><a href="#cpb150207bib39">39</a></span>]</sup> approximation is an average of the two bounds, namely, the lower bound of Voigt and the upper bound of Reuss, which provides the best estimation for the mechanical properties of polycrystalline materials from the elastic constants. In the Voigt average, <sup>[<span class="xref"><a href="#cpb150207bib38">38</a></span>]</sup> the shear modulus and the bulk modulus of a cubic lattice are provided by</p><p><disp-formula id="cpb150207eqn1"><img src="cpb_24_9_096201/cpb150207eqn1.gif"/></disp-formula></p><p><disp-formula id="cpb150207eqn2"><img src="cpb_24_9_096201/cpb150207eqn2.gif"/></disp-formula></p><p>while in the Reuss average, <sup>[<span class="xref"><a href="#cpb150207bib39">39</a></span>]</sup> they are given by</p><p><disp-formula id="cpb150207eqn3"><img src="cpb_24_9_096201/cpb150207eqn3.gif"/></disp-formula></p><p><disp-formula id="cpb150207eqn4"><img src="cpb_24_9_096201/cpb150207eqn4.gif"/></disp-formula></p><p>Therefore, by Hill’ s empirical average, <sup>[<span class="xref"><a href="#cpb150207bib37">37</a></span>]</sup> the shear modulus and the bulk modulus of the polycrystalline material can be expressed as</p><p><disp-formula id="cpb150207eqn5"><img src="cpb_24_9_096201/cpb150207eqn5.gif"/></disp-formula></p><p><disp-formula id="cpb150207eqn6"><img src="cpb_24_9_096201/cpb150207eqn6.gif"/></disp-formula></p><p>We also obtain the static results for the bulk modulus <em>B</em><sub>0</sub> and the pressure derivative of the bulk modulus <inline-formula id="cpb150207ieqn2"><img src="cpb_24_9_096201/cpb150207ieqn2.gif"/></inline-formula> by fitting the static total energy versus lattice constant with the Birch– Murnaghan 3rd-order equation of states (EOS), which are listed in <a anchor="table">Table 1.</a> The derived bulk modulus by fitting EOS turns out to be exactly the same as that from the above VRH approximation, as shown in <a anchor="figure">Fig. 3, </a> which again indicates that our calculations are consistent and reliable. In this work, the calculated bulk modulus is 173.6 GPa for LaB<sub>6</sub>, which agrees well with the result of recent x-ray diffraction studies in Ref. [<span class="xref"><a href="#cpb150207bib40">40</a></span>], 173± 7 GPa. For CeB<sub>6</sub>, the present calculated value is 173.5 GPa, which is considerably close to the previous theoretical result 173 GPa.<sup>[<span class="xref"><a href="#cpb150207bib13">13</a></span>]</sup> For the sake of brevity, we do not enumerate the values one by one for other <em>Ln</em>B<sub>6</sub>. As show in <a anchor="figure">Fig. 3, </a> only small differences appear between each other for the bulk modulus of a range of <em>Ln</em>B<sub>6</sub>, which is due to lower <em>C</em><sub>12</sub> compared with <em>C</em><sub>11</sub>. EuB<sub>6</sub> and YbB<sub>6</sub> are also outliers. In addition, according to Pugh’ s criterion, <sup>[<span class="xref"><a href="#cpb150207bib41">41</a></span>]</sup> the strength fracture is proportional to <em>B</em><sub>0</sub> × <em>a</em><sub>0</sub>, where <em>B</em><sub>0</sub> is the bulk modulus and <em>a</em><sub>0</sub> is the lattice constant. Our calculated <em>B</em><sub>0</sub> × <em>a</em><sub>0</sub> is shown in <a anchor="figure">Fig. 4.</a> It can be seen that <em>B</em><sub>0</sub> × <em>a</em><sub>0</sub> is decreasing for the lanthanide hexaborides, indicating that the strength gets smaller and smaller.</p><p><div class="figure outline_anchor"><div class="figure_anchor" style="display: none; "><b>Fig. 3.</b></div><table><tr><td></td><td align="right" valign="top" ><ul id="sddm"><li><a href="#" onmouseover="mopen('cpb150207f3A')" onmouseout="mclosetime()">Figure Option</a><div id="cpb150207f3A" onmouseover="mcancelclosetime()" onmouseout="mclosetime()"><a class="group3" href="cpb_24_9_096201/cpb150207f3_hr.jpg" title=' <p>The change of bulk modulus <em>B</em><sub>0</sub> with the atomic number of <em>Ln</em> atoms in <em>Ln</em>B<sub>6</sub>. The pink points are derived according to Hill’ s empirical average theory and the blue points are obtained by fitting the Birch– Murnaghan 3rd-order equation of states.</p>'>View</a><a href="cpb_24_9_096201/cpb150207f3_hr.jpg.zip" >Download</a><a href="cpb_24_9_096201/cpb150207f3_hr.jpg.html" target="_blank" >New Window</a></div></li></ul> </td></tr> <tr id="cpb150207f3" ><td align="center" valign="middle"><a class="group3" href="cpb_24_9_096201/cpb150207f3_hr.jpg" title=' <p>The change of bulk modulus <em>B</em><sub>0</sub> with the atomic number of <em>Ln</em> atoms in <em>Ln</em>B<sub>6</sub>. The pink points are derived according to Hill’ s empirical average theory and the blue points are obtained by fitting the Birch– Murnaghan 3rd-order equation of states.</p>'><img src="cpb_24_9_096201/thumbnail/cpb150207f3_hr.jpg" /></a></td><td align="left" valign="middle"><span class="caption"><b>Fig. 3.</b> The change of bulk modulus <em>B</em><sub>0</sub> with the atomic number of <em>Ln</em> atoms in <em>Ln</em>B<sub>6</sub>. The pink points are derived according to Hill’ s empirical average theory and the blue points are obtained by fitting the Birch– Murnaghan 3rd-order equation of states.</span></td></tr></table></div></p><p><div class="figure outline_anchor"><div class="figure_anchor" style="display: none; "><b>Fig. 4.</b></div><table><tr><td></td><td align="right" valign="top" ><ul id="sddm"><li><a href="#" onmouseover="mopen('cpb150207f4A')" onmouseout="mclosetime()">Figure Option</a><div id="cpb150207f4A" onmouseover="mcancelclosetime()" onmouseout="mclosetime()"><a class="group3" href="cpb_24_9_096201/cpb150207f4_hr.jpg" title=' <p>Variation of <em>B</em><sub>0</sub> × <em>a</em><sub>0</sub> for <em>Ln</em>B<sub>6</sub> with the atomic number of <em>Ln</em> atoms.</p>'>View</a><a href="cpb_24_9_096201/cpb150207f4_hr.jpg.zip" >Download</a><a href="cpb_24_9_096201/cpb150207f4_hr.jpg.html" target="_blank" >New Window</a></div></li></ul> </td></tr> <tr id="cpb150207f4" ><td align="center" valign="middle"><a class="group3" href="cpb_24_9_096201/cpb150207f4_hr.jpg" title=' <p>Variation of <em>B</em><sub>0</sub> × <em>a</em><sub>0</sub> for <em>Ln</em>B<sub>6</sub> with the atomic number of <em>Ln</em> atoms.</p>'><img src="cpb_24_9_096201/thumbnail/cpb150207f4_hr.jpg" /></a></td><td align="left" valign="middle"><span class="caption"><b>Fig. 4.</b> Variation of <em>B</em><sub>0</sub> × <em>a</em><sub>0</sub> for <em>Ln</em>B<sub>6</sub> with the atomic number of <em>Ln</em> atoms.</span></td></tr></table></div></p><p>The single crystal shear moduli for the {100} plane along the [010] direction and for the {110} plane along the <inline-formula id="cpb150207ieqn3z"><img src="cpb_24_9_096201/cpb150207ieqn3.gif"/></inline-formula> direction are given by <em>G</em><sub>{100}</sub> = <em>C</em><sub>44</sub> and <em>G</em><sub>{110}</sub> = (<em>C</em><sub>11</sub> – <em>C</em><sub>12</sub>)/2, <sup>[<span class="xref"><a href="#cpb150207bib42">42</a></span>]</sup> respectively. These deformations correspond to a shear and reflect the degree of stability of the crystal with respect to a tetragonal shear. For all compounds, <em>G</em><sub>{110}</sub> is found larger than <em>G</em><sub>{100}</sub>, indicating that it is easier to shear on the {100} plane along the [010] direction than on the {110} plane along the <inline-formula id="cpb150207ieqn3"><img src="cpb_24_9_096201/cpb150207ieqn3.gif"/></inline-formula> direction. Figures 5 and 6 show that the Voigt’ s, Reuss’ s, and Hill’ s shear moduli decrease linearly with increasing atomic number of <em>Ln</em> atoms except for EuB<sub>6</sub> and YbB<sub>6</sub>. This tendency is similar to <em>C</em><sub>44</sub> and is in accordance with the conclusion acquired in Ref. [<span class="xref"><a href="#cpb150207bib12">12</a></span>].</p><p><div class="figure outline_anchor"><div class="figure_anchor" style="display: none; "><b>Fig. 5.</b></div><table><tr><td></td><td align="right" valign="top" ><ul id="sddm"><li><a href="#" onmouseover="mopen('cpb150207f5A')" onmouseout="mclosetime()">Figure Option</a><div id="cpb150207f5A" onmouseover="mcancelclosetime()" onmouseout="mclosetime()"><a class="group3" href="cpb_24_9_096201/cpb150207f5_hr.jpg" title=' <p>The shear modulus <em>G</em> for polycrystalline obtained according to Reuss and Voigt approximations, respectively.</p>'>View</a><a href="cpb_24_9_096201/cpb150207f5_hr.jpg.zip" >Download</a><a href="cpb_24_9_096201/cpb150207f5_hr.jpg.html" target="_blank" >New Window</a></div></li></ul> </td></tr> <tr id="cpb150207f5" ><td align="center" valign="middle"><a class="group3" href="cpb_24_9_096201/cpb150207f5_hr.jpg" title=' <p>The shear modulus <em>G</em> for polycrystalline obtained according to Reuss and Voigt approximations, respectively.</p>'><img src="cpb_24_9_096201/thumbnail/cpb150207f5_hr.jpg" /></a></td><td align="left" valign="middle"><span class="caption"><b>Fig. 5.</b> The shear modulus <em>G</em> for polycrystalline obtained according to Reuss and Voigt approximations, respectively.</span></td></tr></table></div></p><p><div class="figure outline_anchor"><div class="figure_anchor" style="display: none; "><b>Fig. 6.</b></div><table><tr><td></td><td align="right" valign="top" ><ul id="sddm"><li><a href="#" onmouseover="mopen('cpb150207f6A')" onmouseout="mclosetime()">Figure Option</a><div id="cpb150207f6A" onmouseover="mcancelclosetime()" onmouseout="mclosetime()"><a class="group3" href="cpb_24_9_096201/cpb150207f6_hr.jpg" title=' <p>The elastic constant <em>C</em><sub>44</sub> for single crystal and the shear modulus <em>G</em> for polycrystalline obtained based on Hill’ s approximations.</p>'>View</a><a href="cpb_24_9_096201/cpb150207f6_hr.jpg.zip" >Download</a><a href="cpb_24_9_096201/cpb150207f6_hr.jpg.html" target="_blank" >New Window</a></div></li></ul> </td></tr> <tr id="cpb150207f6" ><td align="center" valign="middle"><a class="group3" href="cpb_24_9_096201/cpb150207f6_hr.jpg" title=' <p>The elastic constant <em>C</em><sub>44</sub> for single crystal and the shear modulus <em>G</em> for polycrystalline obtained based on Hill’ s approximations.</p>'><img src="cpb_24_9_096201/thumbnail/cpb150207f6_hr.jpg" /></a></td><td align="left" valign="middle"><span class="caption"><b>Fig. 6.</b> The elastic constant <em>C</em><sub>44</sub> for single crystal and the shear modulus <em>G</em> for polycrystalline obtained based on Hill’ s approximations.</span></td></tr></table></div></p><p><div class="figure outline_anchor"><div class="figure_anchor" style="display: none; "><b>Fig. 7.</b></div><table><tr><td></td><td align="right" valign="top" ><ul id="sddm"><li><a href="#" onmouseover="mopen('cpb150207f7A')" onmouseout="mclosetime()">Figure Option</a><div id="cpb150207f7A" onmouseover="mcancelclosetime()" onmouseout="mclosetime()"><a class="group3" href="cpb_24_9_096201/cpb150207f7_hr.jpg" title=' <p>(a) The Young’ s modulus <em>Y</em>, (b) the Poisson’ s ratio <em>υ </em>, (c) <em>B</em>/<em>G</em>, and (d) Zener anisotropy factor <em>A</em> estimated with Hill’ s approximation.</p>'>View</a><a href="cpb_24_9_096201/cpb150207f7_hr.jpg.zip" >Download</a><a href="cpb_24_9_096201/cpb150207f7_hr.jpg.html" target="_blank" >New Window</a></div></li></ul> </td></tr> <tr id="cpb150207f7" ><td align="center" valign="middle"><a class="group3" href="cpb_24_9_096201/cpb150207f7_hr.jpg" title=' <p>(a) The Young’ s modulus <em>Y</em>, (b) the Poisson’ s ratio <em>υ </em>, (c) <em>B</em>/<em>G</em>, and (d) Zener anisotropy factor <em>A</em> estimated with Hill’ s approximation.</p>'><img src="cpb_24_9_096201/thumbnail/cpb150207f7_hr.jpg" /></a></td><td align="left" valign="middle"><span class="caption"><b>Fig. 7.</b> (a) The Young’ s modulus <em>Y</em>, (b) the Poisson’ s ratio <em>υ </em>, (c) <em>B</em>/<em>G</em>, and (d) Zener anisotropy factor <em>A</em> estimated with Hill’ s approximation.</span></td></tr></table></div></p><p>It is known that the Young’ s modulus, the Poisson’ s ratio, Zener anisotropy factor <em>A</em>, and the ratio of <em>B</em>/<em>G</em> are the noteworthy parameters for materials in technology and engineering applications.<sup>[<span class="xref"><a href="#cpb150207bib43">43</a></span>]</sup> The results are plotted in <a anchor="figure">Fig. 7.</a> These parameters are calculated in terms of the elastic constants <em>C</em><sub><em>ij</em></sub> via the following relations:</p><p><disp-formula id="cpb150207eqn7"><img src="cpb_24_9_096201/cpb150207eqn7.gif"/></disp-formula></p><p><disp-formula id="cpb150207eqn8"><img src="cpb_24_9_096201/cpb150207eqn8.gif"/></disp-formula></p><p><disp-formula id="cpb150207eqn9"><img src="cpb_24_9_096201/cpb150207eqn9.gif"/></disp-formula></p><p>The Young’ s modulus serves as a measurement of the stiffness of a solid and the Poisson’ s ratio evaluates the stability of a crystal against shear.<sup>[<span class="xref"><a href="#cpb150207bib42">42</a></span>]</sup> The relationship between the hardness and the Young’ s modulus is not identical for different materials: the general tendency is that the larger the modulus, the harder the material. The Young’ s modulus decreases with increasing atomic number, which demonstrates that the hardness is reduced gradually for the <em>Ln</em>B<sub>6</sub> compounds except for EuB<sub>6</sub> and YbB<sub>6</sub>. The smaller Poisson’ s ratio indicates that <em>Ln</em>B<sub>6</sub> is relatively stable against shear.<sup>[<span class="xref"><a href="#cpb150207bib36">36</a></span>]</sup> Pugh<sup>[<span class="xref"><a href="#cpb150207bib41">41</a></span>]</sup> introduced the quotient of bulk to shear modulus of polycrystalline phases, where the shear modulus <em>G</em> represents the resistance to plastic deformation while the bulk modulus <em>B</em> represents the resistance to fracture. A high (low) <em>B</em>/<em>G</em> corresponds to ductility (brittleness). The critical value which distinguishes ductile and brittle materials is about 1.75. Our calculated results are displayed in <a anchor="figure">Fig. 7.</a> The <em>B</em>/<em>G</em> of <em>Ln</em>B<sub>6</sub> tends to increase with increasing atomic number except for EuB<sub>6</sub> and YbB<sub>6</sub>. The compounds lighter than SmB<sub>6</sub> present a brittle behavior, while the rest are ductile materials. EuB<sub>6</sub> and YbB<sub>6</sub> are still out of the tendency and they are brittle compounds. The Zener anisotropy factor <em>A</em> is a measure of the degree of elastic anisotropy in a solid. The Zener anisotropy factor takes the value of 1 for a completely isotropic material. The calculated Zener anisotropy factor for <em>Ln</em>B<sub>6</sub> is smaller than 1, which indicates that the compounds are entirely anisotropic.<sup>[<span class="xref"><a href="#cpb150207bib42">42</a></span>]</sup></p></div><div class="paragraph"><span class="paragraph_title outline_anchor" level="2">3.3. Debye temperature</span><p>The thermodynamic parameters such as the Debye temperature and the sound velocity are also essential physical parameters. In the present case, the Debye temperature <em>θ </em><sub>D</sub><sup>[<span class="xref"><a href="#cpb150207bib44">44</a></span>]</sup> is obtained with the calculated elastic constants according to the following relation:</p><p><disp-formula id="cpb150207eqn10"><img src="cpb_24_9_096201/cpb150207eqn10.gif"/></disp-formula></p><p>where <em>h</em> is the Planck constant, <em>k</em> is the Boltzmann constant, <em>N</em><sub>A</sub> is the Avogadro number, <em>n</em> is the number of atoms per formula unit, <em>M</em> is the molecular mass per formula unit, and <em>ρ </em> is the density.</p><div class="table outline_anchor"><div class="table_anchor" style="display: none; "><b>Table 2.</b></div><div class="caption_title" style="display: none; "><b>Table 2.</b></div><table><tr><td class="table-icon-td"><img class="table-icon" src="https://cpb.iphy.ac.cn/html_resources/images/table-icon.gif"/><div style="display: none; " class="table_content"><span class="caption"> <b>Table 2.</b> The calculated density (<em>ρ </em>), the longitudinal, transverse, mean elastic wave velocities (<em>v</em><sub><em>l</em></sub>, <em>v</em><sub><em>t</em></sub>, and <em>v</em><sub>m</sub>), and the Debye temperature (<em>θ </em><sub>D</sub>) for <em>Ln</em>B<sub>6</sub>.</span><table width="100%"><colgroup><col align="center"/><col align="center"/><col align="center"/><col align="center"/><col align="center"/><col align="center"/></colgroup><thead><tr><th align="center" valign="top" style="border-top:1px solid #000; border-bottom:1px solid #000; "/><th align="center" valign="top" style="border-top:1px solid #000; border-bottom:1px solid #000; "><em>ρ </em>/g· cm<sup>− 1</sup></th><th align="center" valign="top" style="border-top:1px solid #000; border-bottom:1px solid #000; "><em>v</em><sub>l</sub>/m· s<sup>− 1</sup></th><th align="center" valign="top" style="border-top:1px solid #000; border-bottom:1px solid #000; "><em>v</em><sub>t</sub>/m· s<sup>− 1</sup></th><th align="center" valign="top" style="border-top:1px solid #000; border-bottom:1px solid #000; "><em>v</em><sub>m</sub>/m· s<sup>− 1</sup></th><th align="center" valign="top" style="border-top:1px solid #000; border-bottom:1px solid #000; "><em>θ </em><sub>D</sub>/K</th></tr></thead><tbody><tr><td align="center" valign="top">LaB<sub>6</sub></td><td align="center" valign="top">4.714</td><td align="center" valign="top">8625</td><td align="center" valign="top">5306</td><td align="center" valign="top">5855</td><td align="center" valign="top">1110</td></tr><tr><td align="center" valign="top">Cal.</td><td align="center" valign="top"/><td align="center" valign="top"/><td align="center" valign="top"/><td align="center" valign="top"/><td align="center" valign="top">1165<span class="xref"><a href="#t2fn1"><sup>a)</sup></a></span></td></tr><tr><td align="center" valign="top">Exp.</td><td align="center" valign="top">4.71<span class="xref"><a href="#t2fn2"><sup>b)</sup></a></span></td><td align="center" valign="top"/><td align="center" valign="top"/><td align="center" valign="top"/><td align="center" valign="top"/></tr><tr><td align="center" valign="top">CeB<sub>6</sub></td><td align="center" valign="top">4.733</td><td align="center" valign="top">8427</td><td align="center" valign="top">5072</td><td align="center" valign="top">5609</td><td align="center" valign="top">1062</td></tr><tr><td align="center" valign="top">Exp.</td><td align="center" valign="top">4.797<span class="xref"><a href="#t2fn3"><sup>c)</sup></a></span></td><td align="center" valign="top"/><td align="center" valign="top"/><td align="center" valign="top"/><td align="center" valign="top">751<span class="xref"><a href="#t2fn4"><sup>d)</sup></a></span></td></tr><tr><td align="center" valign="top">PrB<sub>6</sub></td><td align="center" valign="top">4.795</td><td align="center" valign="top">8288</td><td align="center" valign="top">4928</td><td align="center" valign="top">5457</td><td align="center" valign="top">1036</td></tr><tr><td align="center" valign="top">NdB<sub>6</sub></td><td align="center" valign="top">4.908</td><td align="center" valign="top">8110</td><td align="center" valign="top">4764</td><td align="center" valign="top">5281</td><td align="center" valign="top">1005</td></tr><tr><td align="center" valign="top">PmB<sub>6</sub></td><td align="center" valign="top">4.961</td><td align="center" valign="top">7974</td><td align="center" valign="top">4620</td><td align="center" valign="top">5127</td><td align="center" valign="top">979</td></tr><tr><td align="center" valign="top">SmB<sub>6</sub></td><td align="center" valign="top">5.111</td><td align="center" valign="top">7768</td><td align="center" valign="top">4436</td><td align="center" valign="top">4929</td><td align="center" valign="top">942</td></tr><tr><td align="center" valign="top">Exp.</td><td align="center" valign="top">5.06<span class="xref"><a href="#t2fn3"><sup>c)</sup></a></span></td><td align="center" valign="top"/><td align="center" valign="top"/><td align="center" valign="top"/><td align="center" valign="top"/></tr><tr><td align="center" valign="top">EuB<sub>6</sub></td><td align="center" valign="top">5.009</td><td align="center" valign="top">7745</td><td align="center" valign="top">4701</td><td align="center" valign="top">5194</td><td align="center" valign="top">984</td></tr><tr><td align="center" valign="top">Exp.</td><td align="center" valign="top">4.895<span class="xref"><a href="#t2fn3"><sup>c)</sup></a></span></td><td align="center" valign="top"/><td align="center" valign="top"/><td align="center" valign="top"/><td align="center" valign="top"/></tr><tr><td align="center" valign="top">GdB<sub>6</sub></td><td align="center" valign="top">5.332</td><td align="center" valign="top">7476</td><td align="center" valign="top">4170</td><td align="center" valign="top">4642</td><td align="center" valign="top">891</td></tr><tr><td align="center" valign="top">TbB<sub>6</sub></td><td align="center" valign="top">5.391</td><td align="center" valign="top">7350</td><td align="center" valign="top">4032</td><td align="center" valign="top">4495</td><td align="center" valign="top">864</td></tr><tr><td align="center" valign="top">DyB<sub>6</sub></td><td align="center" valign="top">5.497</td><td align="center" valign="top">7203</td><td align="center" valign="top">3890</td><td align="center" valign="top">4342</td><td align="center" valign="top">835</td></tr><tr><td align="center" valign="top">HoB<sub>6</sub></td><td align="center" valign="top">5.572</td><td align="center" valign="top">7077</td><td align="center" valign="top">3756</td><td align="center" valign="top">4198</td><td align="center" valign="top">808</td></tr><tr><td align="center" valign="top">ErB<sub>6</sub></td><td align="center" valign="top">5.649</td><td align="center" valign="top">6946</td><td align="center" valign="top">3613</td><td align="center" valign="top">4043</td><td align="center" valign="top">779</td></tr><tr><td align="center" valign="top">TmB<sub>6</sub></td><td align="center" valign="top">5.708</td><td align="center" valign="top">6816</td><td align="center" valign="top">3457</td><td align="center" valign="top">3874</td><td align="center" valign="top">748</td></tr><tr><td align="center" valign="top">YbB<sub>6</sub></td><td align="center" valign="top">5.612</td><td align="center" valign="top">6973</td><td align="center" valign="top">4007</td><td align="center" valign="top">4451</td><td align="center" valign="top">849</td></tr><tr><td align="center" valign="top">Exp.</td><td align="center" valign="top">5.53<span class="xref"><a href="#t2fn3"><sup>c)</sup></a></span></td><td align="center" valign="top"/><td align="center" valign="top"/><td align="center" valign="top"/><td align="center" valign="top"/></tr><tr><td align="center" valign="top">LuB<sub>6</sub></td><td align="center" valign="top">5.882</td><td align="center" valign="top">6532</td><td align="center" valign="top">3139</td><td align="center" valign="top">3529</td><td align="center" valign="top">682</td></tr></tbody></table><table-wrap-foot><fn id="t2fn1"><label><sup>a)</sup></label><p>Ref. [<span class="xref"><a href="#cpb150207bib46">46</a></span>], </p></fn><fn id="t2fn2"><label><sup>b)</sup></label><p>Ref. [<span class="xref"><a href="#cpb150207bib29">29</a></span>], </p></fn><fn id="t2fn3"><label><sup>c)</sup></label><p>Ref. [<span class="xref"><a href="#cpb150207bib28">28</a></span>], </p></fn><fn id="t2fn4"><label><sup>d)</sup></label><p>Ref. [<span class="xref"><a href="#cpb150207bib3">3</a></span>].</p></fn></table-wrap-foot></div></td><td align="left" valign="middle"><span class="caption"> <b>Table 2.</b> The calculated density (<em>ρ </em>), the longitudinal, transverse, mean elastic wave velocities (<em>v</em><sub><em>l</em></sub>, <em>v</em><sub><em>t</em></sub>, and <em>v</em><sub>m</sub>), and the Debye temperature (<em>θ </em><sub>D</sub>) for <em>Ln</em>B<sub>6</sub>.</span></td></tr></table></div><p>The average sound velocity <em>v</em><sub>m</sub> of materials can be obtained according to the following formula:</p><p><disp-formula id="cpb150207eqn11"><img src="cpb_24_9_096201/cpb150207eqn11.gif"/></disp-formula></p><p>For the cubic crystal, <em>v</em><sub>l</sub> and <em>v</em><sub>t</sub> are the longitudinal and the transverse elastic wave velocities, which can be obtained from the elastic modulus by the famous Navier’ s equations<sup>[<span class="xref"><a href="#cpb150207bib45">45</a></span>]</sup></p><p><disp-formula id="cpb150207eqn12"><img src="cpb_24_9_096201/cpb150207eqn12.gif"/></disp-formula></p><p><disp-formula id="cpb150207eqn13"><img src="cpb_24_9_096201/cpb150207eqn13.gif"/></disp-formula></p><p>Based on these equations, we derive the corresponding values which are tabulated in <a anchor="table">Table 2.</a> It can be seen that the sound velocity decreases from LaB<sub>6</sub> to LuB<sub>6</sub> except EuB<sub>6</sub> and YbB<sub>6</sub>. As far as we know, there are no available experimental or theoretical values to compare with our results for these parameters. We believe that the Debye temperature we obtained for <em>Ln</em>B<sub>6</sub> is reasonable in comparison with the theoretical Debye temperature for LaB<sub>6</sub> (1165 K)<sup>[<span class="xref"><a href="#cpb150207bib46">46</a></span>]</sup> at zero pressure.</p></div><div class="paragraph"><span class="paragraph_title outline_anchor" level="2">3.4. Electronic structure</span><p>It is clear that the structural and elastic properties of the lanthanide series solid compounds change regularly, which is strongly related to the unique electron configuration of the lanthanide series atoms. From La to Lu, the valence electron configuration is 4f<sup>0− 14</sup>5d<sup>0− 1</sup>6s<sup>2</sup> and electrons are added to the inner unfilled 4f shell continuously with the increasing atomic number, resulting in a continuous but minor change in the elemental properties. As can be seen from <a anchor="figure">Fig. 8, </a> the distribution of the total electronic density of states of <em>Ln</em>B<sub>6</sub> is very similar. The total DOS demonstrates that there is a deep valley close to the Fermi level <em>E</em><sub>F</sub> and this valley is referred to as a pseudogap. This pseudogap indicates the presence of a strong covalent bonding in the B<sub>6</sub> octahedron cage.<sup>[<span class="xref"><a href="#cpb150207bib36">36</a></span>]</sup> There is a relationship between the structural stability and the position of <em>E</em><sub>F</sub> with respect to the pseudogap. From <a anchor="figure">Fig. 8, </a> we observe that the Fermi level falls below the pseudogap in EuB<sub>6</sub> and YbB<sub>6</sub> while is above the pseudogap in the other compounds. This indicates that not all of the bonding states are filled and some extra electrons are required to reach the maximum stability for EuB<sub>6</sub> and YbB<sub>6</sub>. This phenomenon is consistent with the lower bulk moduli of EuB<sub>6</sub> and YbB<sub>6</sub>.</p><p><div class="figure outline_anchor"><div class="figure_anchor" style="display: none; "><b>Fig. 8.</b></div><table><tr><td></td><td align="right" valign="top" ><ul id="sddm"><li><a href="#" onmouseover="mopen('cpb150207f8A')" onmouseout="mclosetime()">Figure Option</a><div id="cpb150207f8A" onmouseover="mcancelclosetime()" onmouseout="mclosetime()"><a class="group3" href="cpb_24_9_096201/cpb150207f8_hr.jpg" title=' <p>Total electron density of states of <em>Ln</em>B<sub>6</sub>: (a) <em>Ln</em> = La, Ce, Pr, Nd, Pm; (b) <em>Ln</em> = Sm, Eu, Gd, Tb, Dy; (c) <em>Ln</em> = Ho, Er, Tm, Yb, Lu.</p>'>View</a><a href="cpb_24_9_096201/cpb150207f8_hr.jpg.zip" >Download</a><a href="cpb_24_9_096201/cpb150207f8_hr.jpg.html" target="_blank" >New Window</a></div></li></ul> </td></tr> <tr id="cpb150207f8" ><td align="center" valign="middle"><a class="group3" href="cpb_24_9_096201/cpb150207f8_hr.jpg" title=' <p>Total electron density of states of <em>Ln</em>B<sub>6</sub>: (a) <em>Ln</em> = La, Ce, Pr, Nd, Pm; (b) <em>Ln</em> = Sm, Eu, Gd, Tb, Dy; (c) <em>Ln</em> = Ho, Er, Tm, Yb, Lu.</p>'><img src="cpb_24_9_096201/thumbnail/cpb150207f8_hr.jpg" /></a></td><td align="left" valign="middle"><span class="caption"><b>Fig. 8.</b> Total electron density of states of <em>Ln</em>B<sub>6</sub>: (a) <em>Ln</em> = La, Ce, Pr, Nd, Pm; (b) <em>Ln</em> = Sm, Eu, Gd, Tb, Dy; (c) <em>Ln</em> = Ho, Er, Tm, Yb, Lu.</span></td></tr></table></div></p><p><div class="figure outline_anchor"><div class="figure_anchor" style="display: none; "><b>Fig. 9.</b></div><table><tr><td></td><td align="right" valign="top" ><ul id="sddm"><li><a href="#" onmouseover="mopen('cpb150207f9A')" onmouseout="mclosetime()">Figure Option</a><div id="cpb150207f9A" onmouseover="mcancelclosetime()" onmouseout="mclosetime()"><a class="group3" href="cpb_24_9_096201/cpb150207f9_hr.jpg" title=' <p>Total and angular-momentum-projected densities of states of (a) EuB<sub>6</sub> and (b)YbB<sub>6</sub>.</p>'>View</a><a href="cpb_24_9_096201/cpb150207f9_hr.jpg.zip" >Download</a><a href="cpb_24_9_096201/cpb150207f9_hr.jpg.html" target="_blank" >New Window</a></div></li></ul> </td></tr> <tr id="cpb150207f9" ><td align="center" valign="middle"><a class="group3" href="cpb_24_9_096201/cpb150207f9_hr.jpg" title=' <p>Total and angular-momentum-projected densities of states of (a) EuB<sub>6</sub> and (b)YbB<sub>6</sub>.</p>'><img src="cpb_24_9_096201/thumbnail/cpb150207f9_hr.jpg" /></a></td><td align="left" valign="middle"><span class="caption"><b>Fig. 9.</b> Total and angular-momentum-projected densities of states of (a) EuB<sub>6</sub> and (b)YbB<sub>6</sub>.</span></td></tr></table></div></p><p><div class="figure outline_anchor"><div class="figure_anchor" style="display: none; "><b><a anchor="figure">Fig. 10</a>.</b></div><table><tr><td></td><td align="right" valign="top" ><ul id="sddm"><li><a href="#" onmouseover="mopen('cpb150207f10A')" onmouseout="mclosetime()">Figure Option</a><div id="cpb150207f10A" onmouseover="mcancelclosetime()" onmouseout="mclosetime()"><a class="group3" href="cpb_24_9_096201/cpb150207f10_hr.jpg" title=' <p>Energy band structure along the principal high-symmetry directions in the Birllouin zone for (a) SmB<sub>6</sub>, (b) EuB<sub>6</sub>, (c) TmB<sub>6</sub>, and (d) YbB<sub>6</sub> in the stable structure.</p>'>View</a><a href="cpb_24_9_096201/cpb150207f10_hr.jpg.zip" >Download</a><a href="cpb_24_9_096201/cpb150207f10_hr.jpg.html" target="_blank" >New Window</a></div></li></ul> </td></tr> <tr id="cpb150207f10" ><td align="center" valign="middle"><a class="group3" href="cpb_24_9_096201/cpb150207f10_hr.jpg" title=' <p>Energy band structure along the principal high-symmetry directions in the Birllouin zone for (a) SmB<sub>6</sub>, (b) EuB<sub>6</sub>, (c) TmB<sub>6</sub>, and (d) YbB<sub>6</sub> in the stable structure.</p>'><img src="cpb_24_9_096201/thumbnail/cpb150207f10_hr.jpg" /></a></td><td align="left" valign="middle"><span class="caption"><b><a anchor="figure">Fig. 10</a>.</b> Energy band structure along the principal high-symmetry directions in the Birllouin zone for (a) SmB<sub>6</sub>, (b) EuB<sub>6</sub>, (c) TmB<sub>6</sub>, and (d) YbB<sub>6</sub> in the stable structure.</span></td></tr></table></div></p><p>In <a anchor="figure">Fig. 9, </a> the total and the partial densities of states (PDOS) are presented for EuB<sub>6</sub> and YbB<sub>6</sub>. The B 2s and 2p hybridization controls the lower bonding peak located at the energy of approximately − 14 eV below the Fermi level.<sup>[<span class="xref"><a href="#cpb150207bib47">47</a></span>]</sup> Such states are typical for all CaB<sub>6</sub> like hexaborides. The B 2s and 2p interactions from intraoctahedron contribute mainly to the upper bonding peaks in the energy range from − 10 eV to − 6 eV. The upper subgroup, which ranges from − 6 eV to the Fermi level, is composed of B 2p orbitals. The contributions are primarily from the interoctahedral bonds except for the range very close to the Fermi level where the intraoctahedral B– B bonds again become important. However, both the B-p and <em>Ln</em>-d states are spread out on both sides of the Fermi level. For the sake of simplicity, we only display the calculated band structures of SmB<sub>6</sub>, EuB<sub>6</sub>, TmB<sub>6</sub>, and YbB<sub>6</sub> along the high symmetry directions in the Brillouin zone in <a anchor="figure"><a anchor="figure">Fig. 10</a>.</a> As we can see, there are dramatic differences between SmB<sub>6</sub> and EuB<sub>6</sub>, and the same as to TmB<sub>6</sub> and YbB<sub>6</sub>. It is amazing to find that small gaps may exist in EuB<sub>6</sub> and YbB<sub>6</sub>, and both of them possess higher internal parameters <em>x</em> (see <a anchor="table">Table 1)</a>. As illustrated in <a anchor="figure">Fig. 9, </a> the band overlap in the Fermi level happens between the B-s and <em>Ln</em>-d states; and as <em>x</em> increases, the <em>Ln</em> atoms are further apart from the B cages, which leads to the raise of the dispersed conduction band. The intra-cage bonding states go down in energy, resulting in the opening of a small gap.</p></div></div><div class="paragraph"><label>4. Conclusion

The lattice constants, elastic properties, and electronic structures of LnB6 (Ln = La, Ce, … , Yb, Lu) have been studied comprehensively by the PAW method within the GGA. The ab initio calculated lattice constants and the elastic properties are in good agreement with the experimental data and other theoretical results available.

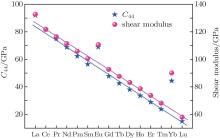
The lattice constants are compressed from LaB6 to LuB6 due to the famous lanthanide contraction effect. The independent elastic constants are investigated and the bulk moduli, shear moduli, Young’ s moduli, Poisson’ s ratios, and Zener anisotropy factors are also estimated for the LnB6 polycrystals. Our results show that the change of the shear modulus is similar to that of C44 and the hardness reduces gradually from LaB6 to LuB6. The analysis of the electronic density of states indicates the presence of a pseudogap. The total densities of states of EuB6 and YbB6 shift towards higher energy, which is inconsistent with their lower bulk moduli. We predict the Debye temperatures for LnB6 and they gradually decrease except for EuB6 and YbB6. The compounds of the divalent Ln elements Eu and Yb are usually exceptions to the trends, which holds mainly for the adoption of their divalent configurations due to their special electron configurations. Since there are no experimental data available for some of these parameters, we believe that our calculated results also provide a reference for future experimental work.

Reference
1 Kauer E 1963 Phys. Lett. 7 171 DOI:10.1016/0031-9163(63)90369-X [Cited within:1]
2 Vand enberg J M, Matthias B T, Corenzwit E and Barz H 1975 Mater. Res. Bull. 10 889 DOI:10.1016/0025-5408(75)90067-7 [Cited within:1]
3 Lüthi B, Blumenröder S, Hillebrand s B, Zirngiebl E, Güntherodt E and Winzer K 1984 Z. Phys. B Condens. Matter 58 31 DOI:10.1007/BF01469434 [Cited within:1]
4 Xu N, Shi X, Biswas P K, Matt C E, Dhaka R S, Huang Y, Plumb N C, Radovi M, Dil J H, Pomjakushina E, Conder K, Amato A, Salman Z, Paul D M, Mesot J, Ding H and Shi M 2013 Phys. Rev. B 88 121102 DOI:10.1103/PhysRevB.88.121102 [Cited within:1]
5 Wolgast S, Kurdak Ç, Sun K, Allen J W, Kim D J and Fisk Z 2013 Phys. Rev. B 88180405(R) DOI:10.1103/PhysRevB.88.180405 [Cited within:1]
6 Weng H M, Zhao J Z, Wang Z J, Fang Z and Dai X 2014 Phys. Rev. Lett. 112 016403 DOI:10.1103/PhysRevLett.112.016403 [Cited within:1]
7 Baranovskiy A E, Grechnev G E, Fil V D, Ignatova T V, Logosha A V, Panfilov A S, Svechkarev I V, Shitsevalova N Y, Filippov V B and Eriksson O 2007 J. Alloys Compd. 442 228 DOI:10.1016/j.jallcom.2006.07.142 [Cited within:1]
8 Wang L, Luo G F, Valencia D, Sierra Llavina C H, Sabirianov R F, Lu J, Lu J Q, Mei W N and Cheung C L 2013 J. Appl. Phys. 114 143709 DOI:10.1063/1.4824285 [Cited within:1]
9 Yu Y, Chen C L, Zhao G D, Zheng X L and Zhu X H 2014 Chin. Phys. Lett. 31 106301 DOI:10.1088/0256-307X/31/10/106301 [Cited within:1]
10 Grechnev G E, Baranovskiy A E, Fil V D, Ignatova T V, Kolobov I G, Logosha A V, Shitsevalova N Y, Filippov V B and Eriksson O 2008 Low Temp. Phys. 34 921 DOI:10.1063/1.3009588 [Cited within:4]
11 Takegahara K, Kasaya M, Goto T and Kasuya T 1985 Phys. B+C 130 49 DOI:10.1016/0378-4363(85)90180-9 [Cited within:1]
12 Nakamura S, Goto T, Kunii S, Iwashita K and Tamaki A 1994 J. Phys. Soc. Jpn. 63 623 DOI:10.1143/JPSJ.63.623 [Cited within:3]
13 Gürel T and Eryiǧit R 2010 Phys. Rev. B 82 104302 DOI:10.1103/PhysRevB.82.104302 [Cited within:3]
14 Gao M C, Rollett A D and Widom M 2007 Phys. Rev. B 75 174120 DOI:10.1103/PhysRevB.75.174120 [Cited within:1]
15 Kresse G and Joubert D 1999 Phys. Rev. B 59 1758 DOI:10.1103/PhysRevB.59.1758 [Cited within:1]
16 Blöchl P E 1994 Phys. Rev. B 50 17953 DOI:10.1103/PhysRevB.50.17953 [Cited within:1]
17 Kresse G and Hafner J 1993 Phys. Rev. B 47 558(R) DOI:10.1103/PhysRevB.47.558 [Cited within:2]
18 Kresse G and Furthmüller J 1996 Comput. Mater. Sci. 6 15 DOI:10.1016/0927-0256(96)00008-0 [Cited within:1]
19 Kresse G and Furthmüller J 1996 Phys. Rev. B 54 11169 DOI:10.1103/PhysRevB.54.11169 [Cited within:1]
20 Monkhorst H J and Pack J D 1976 Phys. Rev. B 13 5390 DOI:10.1103/PhysRevB.13.5188 [Cited within:2]
21 Issa A, Saal J E and Wolverton C 2014 Acta Mater. 65 240 DOI:10.1016/j.actamat.2013.10.066 [Cited within:1]
22 Birch F 1947 Phys. Rev. 71 809 DOI:10.1103/PhysRev.71.809 [Cited within:1]
23 Singh N, Saini S M, Nautiyal T and Auluck S 2007 J. Phys. : Condens. Matter 19 346226 DOI:10.1088/0953-8984/19/34/346226 [Cited within:2]
24 Walker H C, McEwen K A and McMorrow D F 2009 Phys. Rev. B 79 054402 DOI:10.1103/PhysRevB.79.054402 [Cited within:1]
25 Zhang M F, Wang X Q, Zhang X W, Wang P F, Xiong S L, Shi L and Qian Y T 2009 J. Solid State Chem. 182 3098 DOI:10.1016/j.jssc.2009.08.032 [Cited within:1]
26 Takahashi K and Kunii S 1997 J. Solid State Chem. 133 198 DOI:10.1006/jssc.1997.7427 [Cited within:1]
27 Blomberg M K, Merisalo M J, Korsukova M M and Gurin V N 1995 J. Alloys Compd. 217 123 DOI:10.1016/0925-8388(94)01313-7 [Cited within:1]
28 Zherlitsyn S, Wolf B, Lüthi B, Lang M, Hinze P, Uhrig E, Assmus W, Ott H R, Young D P and Fisk Z 2001 Eur. Phys. J. B 22 327 DOI:10.1007/s100520100800 [Cited within:1]
29 Tanaka T, Yoshimoto J, Ishii M, Bannai E and Kawai S 1977 Solid State Commun. 22 203 DOI:10.1016/0038-1098(77)90272-1 [Cited within:1]
30 Lundström T, Lönnberg B, Törmä B, Etourneau J and Tarascon J M 1982 Phys. Scr. 26 414 DOI:10.1088/0031-8949/26/5/012 [Cited within:1]
31 Massidda S, Continenza A, Pascale T M de and Monnier R 1997 Z. Phys. B 102 83 DOI:10.1007/s002570050267 [Cited within:2]
32 Yan X Z, Kuang X Y, Mao A J, Kuang F G, Wang Z H and Sheng X W 2013 Acta Phys. Sin. 62 107402 (in Chinese) DOI:10.7498/aps.62.107402 [Cited within:1]
33 Qi C J, Feng J, Zhou R F, Jiang Y H and Zhou R 2013 Chin. Phys. Lett. 30 117101 DOI:10.1088/0256-307X/30/11/117101 [Cited within:1]
34 Wang S Q and Ye H Q 2003 J. Phys. : Condens. Matter 15 5307 DOI:10.1088/0953-8984/15/30/312 [Cited within:2]
35 Sin’ko G V and Smirnow N A 2002 J. Phys. : Condens. Matter 14 6989 DOI:10.1088/0953-8984/14/29/301 [Cited within:1]
36 Ravindran P, Fast L, Korzhavyi P A, Johansson B, Wills J and Eriksson O 1998 J. Appl. Phys. 84 4891 DOI:10.1063/1.368733 [Cited within:3]
37 Hill R 1952 Proc. Phys. Soc. A 65 349 DOI:10.1088/0370-1298/65/5/307 [Cited within:2]
38 Voigt W 1928 Lehrbuch der Kristallphysik B. G. Teubner Leipzig [Cited within:1]
39 Reuss A and Angew Z 1929 Math. Mech. 9 55 [Cited within:2]
40 Godwal B K, Petruska E A, Speziale S, Yan J, Clark S M, Kruger M B and Jeanloz R 2009 Phys. Rev. B 80 172104 DOI:10.1103/PhysRevB.80.172104 [Cited within:1]
41 Pugh S F 1954 Philos. Mag. 45 823 DOI:10.1080/14786440808520496 [Cited within:2]
42 Yang J W, Gao T and Gong Y R 2014 Solid State Sci. 32 76 DOI:10.1016/j.solidstatesciences.2014.03.019 [Cited within:3]
43 Cai T, Zhang Z J, Zhang P, Yang J B and Zhang Z F 2014 J. Appl. Phys. 116 163512 DOI:10.1063/1.4898319 [Cited within:1]
44 Anderson O L 1963 J. Phys. Chem. Solids 24 909 DOI:10.1016/0022-3697(63)90067-2 [Cited within:1]
45 Sa B S, Zhou J and Sun Z M 2012 Intermetallics 22 92 DOI:10.1016/j.intermet.2011.11.005 [Cited within:1]
46 Xu G L, Chen J D, Xia Y Z, Liu X F, Liu Y F and Zhang X Z 2009 Chin. Phys. Lett. 26 056201 DOI:10.1088/0256-307X/26/5/056201 [Cited within:1]
47 Mogulkoc Y, Ciftci Y O, Kabak M and Colakoglu K 2014 Superlattices Microstruct. 71 46 DOI:10.1016/j.spmi.2014.03.037 [Cited within:1]