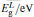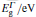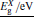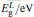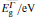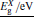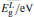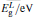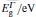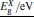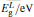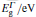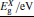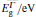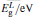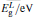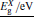Quaternary semiconducting materials are of continuing major concern due to their various technical applications, including light emitting diodes, lasers, optical amplifiers, detectors, frequency mixing components, and electro-optic modulators.^[1] The range of device applications has been broadened in the last few decades by increasing the possibilities of engineering the material properties. The quaternary alloy Ga_xIn_{1 − x}As_yP_{1 − y} is one of the alloys that are particularly important for manufacturing optoelectronic devices. The properties of a material under stress are determined by the elastic constants.^[2] These properties have an important role in determining the binding characteristic between adjacent atomic planes, structural stability, and anisotropic characteristics of binding.^[2] For the mechanical properties, a knowledge of the effect of strain on the electronic properties, specifically the elastic constants which describe the response to an applied macroscopic stress, is required.^[3] Since the advent of nanodevices based on semiconductor materials, the detailed conceptions of these materials under the influence of temperature and pressure have been conveniently determined.^[4]

In the present study, the elastic parameters and the relevant properties of Ga_xIn_{1 − x}As_yP_{1 − y} quaternary alloy lattice matching GaAs substrate are investigated in a composition (y) range of 0– 1, a temperature range from 0 to 500  K, and a pressure range from 0 to 120  kbar. The quaternary alloy Ga_xIn_{1 − x}As_yP_{1 − y} is consisted as the ternary alloys Ga_xIn_{1 − x}As, GaAs_xP_{1 − x}, InAs_xP_{1 − x}, and Ga_xIn_{1 − x}P, which are bounded in their corresponding orders by four binary materials InAs, GaAs, InP, and GaP.

Our calculations are based on the empirical pseudopotential method (EPM) within the virtual crystal approximation (VCA) including the effective disorder potential.^{[5– 22]} We also study the variations of the mechanical properties of interest for the Ga_xIn_{1 − x}As_yP_{1 − y}/GaAs system with temperatures and pressures. The calculated results for the binary parent compounds GaP, GaAs, InP, and InAs show good agreement with the available experimental and published data.

The rest of this paper is organized as follows. In Section  2, we briefly describe the calculation method. Our results and discussion are given in Section  3. And our conclusion is presented in Section  4.

Initially, the energy band gaps of the binary parent compounds GaAs, GaP, InAs, and InP are calculated by using EPM. In EPM, one needs to solve the Schrö dinger equation in which the one-electron pseudo-potential is represented by a linear superposition of the atomic potentials which are adjusted to fit well with the experimental values at the selected points L, Γ , and X in the Brillouin zone.

The band gap energies are estimated by numerically solving the secular determinant equation^{[12, 13]}

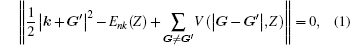
where

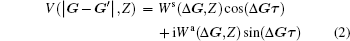
is the Z-dependent pseudo-potential, and Z may be pressure p or temperature T.

The symmetrical W^s and anti-symmetrical W^a form factors of the parent binary compounds of Ga_xIn_{1 − x}As_yP_{1 − y} are deduced by fitting the calculated band gap energies to match the experimental values available in the literature. The temperature- and pressure-dependent form factors are obtained from the assumed relations^{[5, 6]}

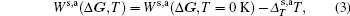
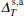
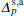
where and are the temperature- and pressuredependent coefficients of the form factors, respectively.^{[5, 6]}

The temperature- and pressure-dependent lattice constants of the binary compounds are calculated from the following relations:^[21]

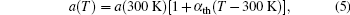
where α _th, B, and B′ are constants cited from Ref.  [21].

The band gap energies of the parent binary compounds GaAs, InP, GaP, and InAs at different temperatures and pressures are displayed in Table  1. A comparison between our calculated data and the published ones show that they are in excellent agreement with each other. Table  2 shows the adjusted form factors of the binary materials GaAs, GaP, InP, and InAs for various temperatures and pressures.

The next step is to study the band gap energies of the associated ternary compounds, namely, Ga_xIn_{1 − x}As, GaAs_xP_{1 − x}, InAs_xP_{1 − x}, and Ga_xIn_{1 − x}P_y, and deduce their bowing parameter energies which are used to calculate the form factors of the quaternary alloy of interest,

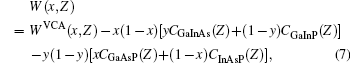
with

whereC_GaInAs(Z), C_GaInP(Z), C_GaAsP(Z), andC_InAsP(Z) are the Z-dependent bowing parameters of the associated ternary alloys.

Table  3 shows the bowing parameters of the considered ternary alloys Ga_xIn_{1 − x}As, GaAs_xP_{1 − x}, InAs_xP_{1 − x}, and Ga_xIn_{1 − x}P_y at different pressures and temperatures in comparison with the available experimental values.^{[26– 29]}

The lattice constants of the quaternary Ga_xIn_{1 − x}As_yP_{1 − y} alloys are calculated by using Vegard’ s rule^[30]

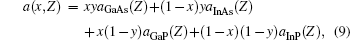
where a_GaAs, a_InAs, a_GaP, and a_InP are the Z-dependent lattice constants of the binary compounds GaAs, InAs, GaP, and InP, respectively.

The lattice matching of Ga_xIn_{1 − x}As_yP_{1 − y} alloy to GaAs substrate gives a relationship between the Ga and As concentrations (x and y)^[14]

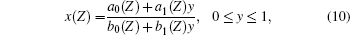
wher

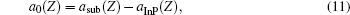
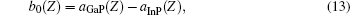
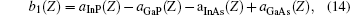
with a’ s being the Z-dependent lattice constants of the binary compounds. The lattice constants of the binary compounds InAs, GaP, InP, and GaAs at different temperatures and pressures are displayed in Table  4.

Table 1.

Table 1.

Table 1. Energy band gaps at different temperature and pressure for the parent binary compounds GaAs, InAs, InP, and GaP. Effect of temperature at p= 0  kba T/K GaAs GaP InAs InP 0 1.7428 1.519  1.519a) 1.7796 2.6988 2.7523 2.3254  2.340d) 1.1064 0.417  0.417d) 1.3101 1.8938 1.422  1.422d) 2.1544 300 1.6957  1.4318  1.425b) 1.7643  2.5959 2.5781 2.2635  2.2689d) 1.0776 0.3637  0.3637d) 1.3041 1.8586 1.3582  1.3582d) 2.1444  500 1.6641  1.3735  1.3270c) 1.7539  2.4511 2.3412 2.1618  2.1838d) 1.0583 0.3281  0.3281d) 1.3000 1.8164 1.2873  1.2873d) 2.1239 Effect of pressure at T = 300  K p/kbar GaAs GaP InAs InP 0 1.7375 1.4318 1.425b) 1.7921 2.5959 2.5781 2.2635  2.2689d) 1.0776 0.3637 0.3637d) 1.3041 1.8532 1.3582  1.3582d) 2.1404 30 1.9398 1.7499 1.7857 1.5051 2.4035 0.92878 1.2171 0.6973 1.2953 1.9459 1.596 2.1162 60 2.1211 2.0287 1.7808 1.5051 2.4035 0.92878 1.3739 1.0402 1.3155 2.0459 1.842 2.1082 90 2.2795 2.2636 1.7727 1.5051 2.4035 0.92878 1.5415 1.3881 1.3558 2.1509 2.088 2.1126 a) Ref.  [23], b)Ref.  [24], c)Ref.  [21], d)Ref.  [25]

Table 1. Energy band gaps at different temperature and pressure for the parent binary compounds GaAs, InAs, InP, and GaP.

Table 2.

Table 2.

Table 2. The adjusted form factors of the binary materials GaAs, GaP, InP, and InAs for various temperatures and pressures. Effect of temperature at p = 0  Kba T/k GaAs GaP 0 − -0.11970 0.006301 0.030850 0.030311 0.025011 0.005001 − -0.122349 0.013649 0.038835 0.045149 0.031649 0.010149 300 − -0.11990 0.006299 0.029850 0.030259 0.024999 0.004999 − -0.122499 0.013499 0.036999 0.044999 0.031499 0.009999 500 − -0.12004 0.006298 0.029183 0.030224 0.024991 0.004998 − -0.1225995 0.013399 0.034515 0.044899 0.031399 0.009899 InAs InP 0 − -0.105375 0.000100 0.023791 0.022674 0.022494 0.004974 − -0.11490 0.005100 0.028394 0.035100 0.025100 0.005100 300 0.105399 0 0.023300 0.022599 0.022419 0.004899 − -0.11500 0.005000 0.027762 0.035000 0.025000 0.005000 500 − -0.105415 − -0.00006 0.022973 0.022549 0.022369 0.004849 − -0.11506 0.004933 0.027055 0.034933 0.024933 0.004933 Effect of pressure at T = 0  300 k p/kba GaAs GaP 0 − -0.11990 0.006299 0.029850 0.030259 0.024999 0.004999 − -0.12249 0.013499 0.036999 0.044999 0.031499 0.009999 60 − -0.11409 0.007299 0.033550 0.043741 0.025999 0.005999 − -0.12249 0.013509 0.041200 0.045009 0.031509 0.010009 120 − -0.10827 0.008299 0.037250 0.057223 0.026999 0.006999 − -0.12248 0.013519 0.044600 0.045019 0.031519 0.010019 InAs InP 0 0.1053990 0.023300 0.022599 0.022419 0.004899 − -0.11500 0.005000 0.027762 0.035000 0.025000 0.005000 60 − -0.105355 0.000044 0.030814 0.022643 0.022463 0.004943 − -0.11473 0.005267 0.033465 0.035267 0.025267 0.005267 120 − -0.105311 0.000088 0.038328 0.022687 0.022507 0.004987 − -0.11446 0.005533 0.039039 0.035533 0.025533 0.005533

Table 2. The adjusted form factors of the binary materials GaAs, GaP, InP, and InAs for various temperatures and pressures.

Table 3.

Table 3.

Table 3. Bowing parameters of the parent ternary alloys at various temperatures and pressures. Temperature effect at p= 0  kbar GaxIn1 − xAs GaxIn1 − xp T= 0  K T= 300  K T= 500  K T= 0  K T= 300  K T= 500  K bΓ bX bL bΓ bX bL bΓ bX bL bΓ bX bL bΓ bX bL bΓ bX bL 0.40 0.44 0.40 0.37 0.34 0.31 0.48 0.46 0.42 0.44 0.43 0.45 0.48 0.39 0.48 0.52 0.37 0.5 0 0.48a) 0.33a) 0.40b) 0.60a) 0.20a) 0.60b) 0.35c) 0.46c) GaASxp1 − x InAsxp1 − x 0.12 0.33 0.22 0.18 0.30 0.26 0.22 0.28 0.28 0.22 0.22 0.19 0.22 0.22 0.19 0.21 0.22 0.18 0.19a) 0.24a) 0.16a) 0.21d) 0.25d) 0.10a) 0.27a) 0.27a) Pressure effect at T= 300  k GaxIn1 − xAs GaxIn1 − xp p= 0  Kbar p= 60  Kbar p= 120  Kbar p= 0  Kbar p= 60  Kbar p= 120  Kbar bΓ bX bL bΓ bX bL bΓ bX bL bΓ bX bL bΓ bX bL bΓ bX bL 0.37 0.40c) 0.34 0.31 0.42 0.50 0.38 0.32 0.08 0.30 0.48  0.60b) 0.39 0.48 0.33 0.33 0.45 0.19 0.28 0.43 Pressure effect at T= 300  k GaAsxP1 − x InAsxp1 − xp 0.18 0.21t 0.30 0.26  0.25d) 0.06 0.12 0.16 0.20 − -0.48 0.28 0.22 0.22 0.19 0.19 0.20 0.17 0.15 0.19 0.14 a) Ref.  [26], b)Ref.  [28], c)Ref.  [27], d)Ref.  [29]

Table 3. Bowing parameters of the parent ternary alloys at various temperatures and pressures.

Table 4.

Table 4.

Table 4. Lattice constants of the binary compounds at different temperature and pressure. Lattice constant Å T= 0  K, p= 0  kbar T= 300  K, p= 0  kbar T= 500  K, p= 0  kbar T= 300  K, p= 60  kba T= 300  K, p= 120  kbar aInP 5.8605 5.8686 5.8740 5.7327 5.6322 aGaAs 5.6431 5.6533 5.6601 5.5267 5.4317 aInAs 6.0492 6.0583 6.0644 5.8907 5.7745 aGaP 5.4432 5.4508 5.4559 5.3440 5.2613

Table 4. Lattice constants of the binary compounds at different temperature and pressure.

The important parameter required to calculate the elastic constants of the Ga_xIn_{1 − x}As_yP_{1 − y} /GaAs quaternary system is its polarity, which is defined by Vogl^[31] as

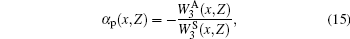
where and are the x and Z-dependent symmetric and anti-symmetric form factors at G(1, 1, 1), respectively.

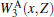
The cubic crystal has only three elastic constants C₁₁, C₁₂, and C₄₄, so we calculate them by using the simplified forms^{[32, 35]}

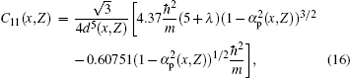
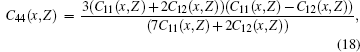
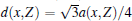
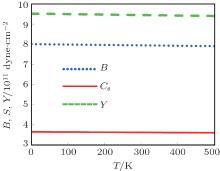
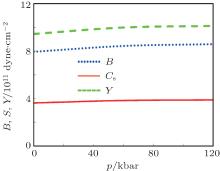
where d(x, Z) is the nearest-neighbor distance given by , and λ is a dimensionless parameter which has a constant value.^[32]

The knowledge of the elastic constants C₁₁, C₁₂, and C₄₄ at different pressures and temperatures allows us to calculate the corresponding Young’ s (Y₀), shear (C_s), and bulk (B) moduli as follows:^{[34, 35]}

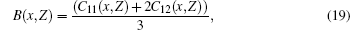
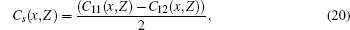
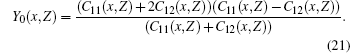
The polarities of the quaternary alloys Ga_xIn_{1 − x}As_yP_{1 − y} lattice matching GaAs substrate are calculated with various compositions y at different temperatures and pressures. The elastic constants C₁₁, C₁₂, and C₄₄ and the corresponding mechanical properties, such as bulk, shear, and Young’ s moduli, of the Ga_xIn_{1 − x}As_yP_{1 − y}/GaAs system are investigated. The variations of all of the properties of interest under the influence of temperature and pressure are investigated. A comparison between our calculated results and the available experiment and published data for the binary parent compounds shows that they have a very good agreement, while the calculated results for the quaternary alloys at various temperatures and pressures may be taken as a reference.