†Corresponding author. E-mail: wyl@hit.edu.cn
‡Corresponding author. E-mail: zw_lu@sohu.com
*Project supported by the National Natural Science Foundation of China (Grant Nos. 61378007 and 61138005) and the Fundamental Research Funds for the Central Universities, China (Grant No. HIT. IBRSEM. A. 201409).
Brillouin amplification is a new method to obtain high power hundred-picosecond laser pulses for shock ignition. The laser pulse’s intensity can be amplified to 10 GW/cm2 through this method. In order to determine the near-field quality, the relationship between the Brillouin amplification gain and the B integral in the stimulated Brillouin scattering (SBS) energy transfer process was studied, and numerical simulations and calculations were carried out to explain the process. For achieving an output intensity of 10 GW/cm2 under the condition that the effect of small–scale self-focusing is insignificant in the Brillouin amplification, the influence of the configuration parameters on the Brillouin amplification and the B integral was investigated. The results showed that the 10 GW/cm2 high power output can be obtained by optimizing the intensities of the pump and Stokes light and choosing an appropriate SBS medium.
In 2007, Betti[1, 2] came up with the idea of shock ignition to achieve inertial confinement fusion. This method divides the laser pulse into two parts: a compression part and a shock part. It has a higher neutron efficiency than the traditional method. However, in the process of shock ignition, how to obtain the desired high peak power laser pulse is a key problem that needs to be solved.
Different from the traditional ignition method, the shock ignition needs a 200 ps laser pulse with an intensity of 10– 20 GW/cm2 as the shock part.[3] Amplifying a seed pulse to such a high intensity challenges the traditional laser amplification technologies. For using the CPA method, the fabrication of large diameter gratings with high damage threshold is still a problem. The traditional MOPA method is also inappropriate, because its amplification efficiency is very low. Brillouin amplification[4] offers a new method for the amplification of the 200 ps laser pulse.
The Brillouin amplifier (shown in Fig. 1) features significant small-signal gain, [5] high signal-to-noise ratio, [6] broad wavelength range, [7] and the capability of pulse compression with short-duration impulse amplification.[8] It stands out from the traditional methods of laser amplification. Through stimulated Brillouin scattering (SBS), energy transferring to get 200 ps laser pulse produces a novel way to obtain a high power short pulse.[9] Lots of research has confirmed that Brillouin media with a short phonon lifetime are helpful to obtain hundred-picosecond laser pulses.[8– 10] The theoretical calculations and experimental data supported Brillouin amplification as an efficient method to amplify hundred-picosecond laser pulses. However, when the amplified high-power pulse transmits in the nonlinear medium, the influence of self-focusing on the quality of the output laser must be considered.
Similar to the conventional laser amplifier, when designing the Brillouin amplifier, the impact of small-scale self-focusing on the beam quality after amplification should be taken into consideration. This is essential for the design of the Brillouin amplifier. Bespalov and Talanov[11] first proposed the B– T theory to explain the small-scale modulation on self-focusing. Later, the researchers at the Livermore laboratory improved the theory. They drew the conclusion that the B integral should be controlled to be no greater than 1.8 through some damaging experiments.[12, 13] If the B integral is above 1.8, the small-scale self-focusing phenomenon may be obvious. Wen et al.[14, 15] investigated the small-scale self-focusing in non-paraxial beam transmission by using the linear perturbation theory. They found that the laser intensity is the main influencing factor on the small-scale self-focusing.
In this paper, we choose three kinds of commonly used fluorocarbons as options for the final Brillouin amplifier. Their amplifying ability is calculated. The structural parameters and the laser parameters are also taken into consideration. Small-scale self-focusing is greatly related to the medium’ s nonlinear refractive index. Through theoretical calculations, the B integral in the Brillouin amplification progress is analyzed. According to our theoretical calculations, the parameters of the final Brillouin amplifier are optimized. To the best of our knowledge, this is the first study of the small-scale self-focusing in the Brllouin amplifying process.
The rest of this paper is divided into three sections as follows. Brllouin amplifying and the B integral theory are presented in Section 2. Section 3 contains our simulation results and analyses. Finally, in Section 4, our work is summarized.
As the pulse width of the injected seed light is 200 ps, it is necessary to consider the effect of the time’ s second derivative in the acoustic field. The SBS super transient coupled wave equations[10] are
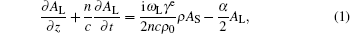
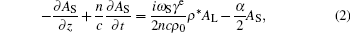
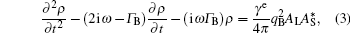
where AL and AS are the pumping and the Stokes complex amplitudes, n is the refractive index of the medium, c is the speed of light, γ e is the electrostrictive coefficient, ρ is the density wave in the medium, B is the Brillouin width, α is the absorption coefficient, and qB represents the sonic frequency in the medium.
In general, the B integral represents the growth of the amplitude modulation. The B integral expression in the international system of units is

where γ is the nonlinear refractive index of the medium, λ 0 is the laser’ s wavelength, and I0 is the laser intensity, which can be calculated by the square of the complex amplitude.
For the Brillouin amplification process, the analytical solution of the amplitude modulation is hard to get, while its numerical solution can be obtained. In this paper, the simulations of Stokes light magnification and its B integral have been carried out in different kinds of media.
According to the theoretical analysis and experimental results in the previous papers, the medium with high gain coefficient and small phonon lifetime should be selected to achieve 200 ps Brillouin amplification. Meanwhile, the medium’ s damage threshold should be taken into consideration. In 1990s, Yoshida et al.[16] found FC-72, FC-75, etc., per-fluorinated hydrocarbons as new SBS media. Then in 2006, they found a series of per-fluorinated hydrocarbons, per-fluorinated amines, and per-fluorinated ether as SBS media.[17] These new SBS media have similar frequency shift, low absorption, and small phonon lifetime. And they also have advantages of high damage threshold and stable chemical properties. So it is conducive to high power high energy SBS amplification experiments. Some parameters of these media are shown in Table 1.
| Table 1. Parameters of Brillouin media. |
The nonlinear refractive indices of the above media are obtained by the Z-scan method. Firstly, the theoretical simulation is carried out on FC-40, because it has the max nonlinear refractive index among the three chosen media. The power intensity of the injected 200 ps Stokes light pulse is set to 1 GW/cm2. The pumping light is a 4-order super-Gaussian beam. 3 ns and 5 ns pump light are simulated respectively. The results are shown in Fig. 2.
 | Fig. 2. Simulation results of FC-40, the Stokes light is 1 GW/cm2, and the pumping light is 1 GW/cm2 with a pulse width of (a) 3 ns and (b) 5 ns. |
In the Brillouin amplification process, as we all know, the light interacts with the acoustic wave in the medium. When the pump and the Stokes light meet in the medium, the electrostrictive effect occurs that changes the refractive index of the medium. In this way, the Brillouin amplification is realized. In order to make full use of the medium, the meeting position of the two pulses is controlled when the Stokes light enters into the medium.
As can be seen from the theoretical results, the growth trends of the magnification and the B integral are very similar before they reach the gain saturation. The gain saturation with the 3 ns pump light is because the Stokes light has got away from the pump light, then the Stokes light cannot be further amplified from this point. Because the nonlinear index coefficient of FC-40 is a little higher, the B integral grows fast in the amplification process. For obtaining the expected output laser of 10 GW/cm2 with the 1 GW/cm2 injected Stokes light, the B integrals should be 2.670 (Fig. 2(a)) and 2.875 (Fig. 2(b)).
In order to obtain the output Stokes light of 10 GW/cm2 and control the B integral under 1.8, the pumping light’ s peak power should be increased. The cell length of the Brillouin amplification medium is set to 30 cm. Increase the pumping light’ s peak power from 300 MW/cm2 to 2 GW/cm2, maintain the Stokes light’ s peak power at 1 GW/cm2, the theoretical result is shown in Fig. 3.
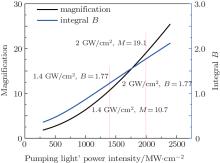 | Fig. 3. Simulation results of FC-40, the Stokes light is 1 GW/cm2, and the pumping pulse width is 5 ns. |
By increasing the pumping light’ s peak power, as G = gIL, the Stokes light can obtain higher gain under the condition of fixed cell length. The peak power intensity of the pumping light is set to 2 GW/cm2. The theoretical simulation is conducted under such conditions and the result is shown in Fig. 4.
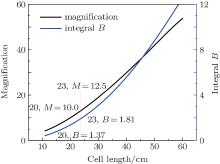 | Fig. 4. Simulation results of FC-40, the Stokes light is 1 GW/cm2, and the pumping light is 2 GW/cm2 with a pulse width of 5 ns. |
When obtaining the 10 GW/cm2 output Stokes light, the B integral in the amplification system is 1.37. In promise of the B integral under 1.8, 12.5 times amplification of the Stokes light could be obtained; these simulation results show that increasing the pump light’ s power intensity is an effective way of achieving this.
When choosing FC-70 as the amplifying medium, its gain coefficient is probably an order of magnitude lower than that of FC-40. At this time, it is hard to obtain the 10 GW/cm2 output Stokes light under the condition of 1 GW/cm2 input. The peak power intensity of the injected 200 ps Stokes light pulse is set to 2 GW/cm2, as well as the pump light, the theoretical result is shown in Fig. 5.
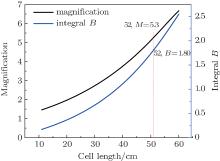 | Fig. 5. Simulation results of FC-70, the Stokes light is 2 GW/cm2, and the pumping light is 2 GW/cm2 with a pulse width of 5 ns. |
When obtaining the 10 GW/cm2 output Stokes light, the B integral in the amplification system is 1.80. FC-70 has a smaller nonlinear refractive index than FC-40, its Brillouin gain is too low, so it is difficult to obtain the 10 GW/cm2 output Stokes light. In a word, FC-70 does not perform well in Brillouin amplification.
Finally, we study FC-43 as the amplifying medium, the peak power intensity of the injected 200 ps Stokes light pulse is set to 1 GW/cm2, while the pump light’ s peak power is set to 2 GW/cm2. The theoretical result is shown in Fig. 6.
 | Fig. 6. Simulation results of FC-43, the Stokes light is 1 GW/cm2, and the pumping light is 2 GW/cm2 with a pulse width of 5 ns. |
It can be seen that FC-43 has a smaller nonlinear refractive index than FC-40, and its Brillouin gain is higher than FC-70, the result is much better than that of FC-70. When obtaining the 10 GW/cm2 output Stokes light, the B integral in the amplification system is 0.98. In promise of the B integral under 1.8, 17.4 times amplification of the Stokes light could be obtained. In inhibition of the B integral, FC-43 is the best among the three kinds of media.
The above simulation results show that small-scale self-focusing is still a problem that cannot be avoided in the Brillouin amplification process. When selecting a Brillouin amplification medium, not only the gain coefficient but also the nonlinear refractive index of the medium should be taken into consideration. The above simulation results show that FC-43 is the best choice among the three kinds of media.
Through the SBS coupled wave equations and the NLS equation, the B integral in the Brillouin energy transfer amplification process was analyzed and calculated for 3 kinds of FC series media. In promise of that the B integral is under 1.8 and 10 GW/cm2 output Stokes light can be obtained in the Brillouin amplification process, the power intensity of the input pumping light should be a little higher than that of the Stokes light. It is found that FC-43 is better than the other two kinds of media. Meanwhile the selected Brillouin medium’ s nonlinear refractive index should be no higher than 4.00× 10− 16 cm2/W so as not to cause a too large B integral. For high-power Brillouin amplification experiments in the future, our result has a reference value.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|



