The quantum coherent effect in a light– atom interaction system plays an important role in controlling the optical property of the medium. An outstanding instance is electromagnetically induced transparency (EIT), ^{[1– 4]} which occurs in the Λ -type three-level atomic system. The transition between the excited and the ground states of the three-level atom is coupled by a weak probe laser, while the transition between the excited and the metastable states is coupled by a strong coherent controlling laser. Under appropriate conditions, the atomic medium becomes transparent for the weak probe field in a very narrow frequency range owing to the destructive interference between two absorption pathways. Recently, the concept of EIT has been extended to the few-photon limit within a high-finesse cavity, ^[2] where the controlling laser is replaced by a single quantized cavity mode with only a few photons. Furthermore, the extreme situation is called the vacuum induced transparency (VIT), ^{[5, 6]} where the controlling laser is replaced by a vacuum cavity field with strong atom– cavity coupling.

Besides, there is a quantum coherent effect in the two-level atomic system, which is similar to the EIT phenomenon and is called the coherent population oscillation (CPO).^{[7, 8]} The CPO occurs in the two-level system coupled to a weak probe laser and a strong coherent driving laser, where the couplings lead to the oscillation of the ground state population at the beat frequency of the two lasers. If the driving field is strong enough and the damping rate of the atomic coherence is much larger than the decay rate of the excited state population, then the probe response of the atomic medium will be significantly modified, i.e., a narrow dip will be created in the absorptive spectrum.^[9] The result of the CPO is similar to that of the EIT, except that the absorption dip of the CPO is not close to zero.

In this paper, we find that VIT, an outstanding instance of an EIT-like phenomenon, can be realized not only in the Λ -type three-level atomic system but also in a relatively simpler two-level atomic system. As mentioned above, the VIT in the three-level system can be regarded as the few-photon case of the EIT. The VIT realized in our two-level system in fact extends the CPO to the few-photon limit. Moreover, the absorption dip of the VIT in our two-level system can be close to zero, which is superior to that of the CPO. The VIT realized in our scheme originates from the coupling between the atomic ensemble and the cavity field in the absence of external driving. When the collectively enhanced atom– cavity coupling is strong enough and the cavity decay rate is much less than the atomic damping rate, the VIT emerges clearly in the two-level system. The EIT-like phenomenon, which shows greatly reduced absorption and enhanced normal dispersion, plays a central role in the generation of slow light. There have been a series of researches on the slow light based on the EIT, ^{[10– 13]} VIT, ^[5] and CPO.^{[9, 14– 17]} Our scheme also provides another candidate. We demonstrate that the VIT in the two-level system is particularly suitable for the generation of slow light, and a group velocity close to 10  m/s is obtained with realistic parameters.

This paper is organized as follows. In Section  2, we present our model and its corresponding Hamiltonian. In Section  3, the dynamics and the optical response of the atomic ensemble are studied, including the EIT-like phenomenon, the analysis of the vacuum Rabi splitting, and the slow light. Finally, a discussion and a brief conclusion are given in Section  4.

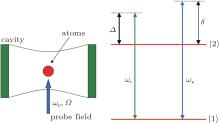
The studied system is comprised of a two-level atomic ensemble and a single-mode cavity in the absence of an external driving field. The atoms coupled to the cavity mode are probed by a weak laser field. The model Hamiltonian reads^[18]

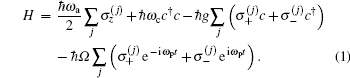
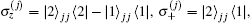
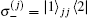
Here and are the Pauli matrices for the j-th atom with | 1〉 _j and | 2〉 _j being the corresponding ground and excited states; c and c^† are the bosonic annihilation and creation operators of the single-mode cavity field; and ω _a, ω _c, and ω _p are the frequencies of the atomic transition, the cavity field, and the probe field, respectively. The coupling coefficient g between the cavity and the atom is the vacuum Rabi frequency, and Ω = dε /(2ħ ) is the coupling strength (Rabi frequency) between the atom and the probe laser with E = ε e^{− iω _pt}/2 + c.c. being the probe field intensity and d the atomic transition dipole moment constant. Here we have used the rotating wave approximation and assumed that the size of the atomic ensemble is much smaller than the related optical wavelength of the cavity field so that the (real) coupling coefficients g and Ω are identical for all the atoms.

To simplify Hamiltonian (1), we define the collective operators of the atomic ensemble

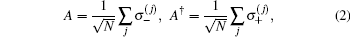
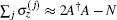
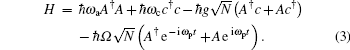
where N is the number of the atoms. In the limit of large N and under the low-excitation condition, the collective operators approximatively satisfy the bosonic commutation relation [A, A^† ] ≈ 1, and further .^{[19– 21]} In terms of these collective bosonic operators, Hamiltonian (1) can be written as

Here the existence of the factor 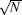means that the coupling coefficients are collectively enhanced.^[22] From Eq.  (3), one knows that the model can be described as that of two coupled bosonic modes probed by a single laser.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Schematics of the two-level atomic ensemble coupled to a high-finesse cavity and probed by a weak laser field.

The dynamics of the system is determined by the quantum Langevin equations^[23]

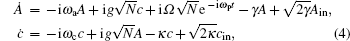
where γ and κ are the atomic damping rate and the cavity decay rate, respectively; A_in (c_in), whose mean value is equal to zero, is the noise operator indicating the action of the reservoir on the atomic system (cavity). Here we have assumed that the atomic collisional dephasing rate is negligible.

From the quantum Langevin equations (4), we can obtain the susceptibility, which actually reflects the optical response of the atomic ensemble. Taking the average

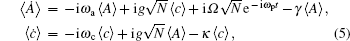
and supposing 〈 A〉 and 〈 c〉 ∝ e^{− iω _pt}, we can immediately obtain the mean value of the collective operator A at the steady state

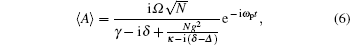
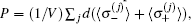
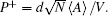
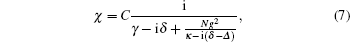
where δ = ω _p – ω _a is the detuning between the probe field and the atomic transition, and Δ = ω _c – ω _a is the detuning between the cavity field and the atomic transition. The polarization of the atomic ensemble is where V is the volume of the atomic ensemble, so its positive frequency part is Then combining with in Eq.  (2), we find Furthermore, we know that the positive frequency part of the probe field intensity is E⁺ = ε e^{− iω _pt}/2. Thus, from the relation P⁺ = χ ε ₀E⁺ , we can obtain the susceptibility

where C = (d²/(ħ ε ₀))(N/V). The term proportional to g² in the denominator of Eq.  (7) reflects the role of the atom– cavity coupling, and N indicates that the coupling can be collectively enhanced. Equation  (7) can be reduced to the result of bare atoms when g = 0, which means the existence of the cavity effectively modifies the optical response of the atoms, although the cavity is initially in the vacuum state. In this sense, we call it the vacuum induced transparency phenomenon.

The real and imaginary parts of the susceptibility are related to the dispersion and absorption, respectively. For the case of bare atoms in the absence of the cavity, i.e., g = 0, Imχ has a Lorentzian shape with an absorption peak located at the atomic resonance, while Reχ displays an anomalous dispersion in the vicinity of the line center, as shown in Fig.  2(a). Under the control of the cavity vacuum field, the EIT-like coherent phenomenon emerges when κ ≪ γ and the strong collectively enhanced coupling Ng² ⩾ κ γ . For simplicity, we first consider the case of Δ = 0. From Fig.  2(b), we can see that Imχ has a narrow dip, while Reχ displays the strong normal dispersion in the vicinity of the line center. To show how Ng² and κ influence the susceptibility, we first fix the cavity decay rate at κ = 0.01γ ; we can see in Fig.  3 that the absorption at the line center becomes markedly reduced with increasing strength of the atoms– cavity coupling, while the slope of the normal dispersion at δ = 0 reaches its maximum when Ng² = κ γ + 2κ ² ≈ κ γ . Then we turn to confine the strong coupling condition, e.g., Ng² = 10κ γ ; in Fig.  4, it is clear that with decreasing decay rate of the cavity, the width of the dip in the absorption spectrum becomes narrower and the slope of the normal dispersion at δ = 0 becomes larger.

Fig.  2.

	Figure Option ViewDownloadNew Window
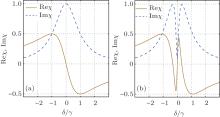	Fig.  2. The real and imaginary parts of the susceptibility as a function of δ for (a) g = 0 or (b) Ng2 = 10κ γ with κ = 0.01γ and Δ = 0.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. The (a) real and (b) imaginary parts of the susceptibility as a function of δ for different coupling strengths when Δ = 0 and the fixed cavity decay rate κ = 0.01γ .

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. The (a) real and (b) imaginary parts of the susceptibility as a function of δ for different cavity decay rates when Δ = 0 and the confined strong coupling condition Ng2 = 10κ γ is satisfied.

Note that in Figs.  2– 4, we have considered the simplest resonant case of Δ = 0. In this case, the imaginary (real) part of the susceptibility is a symmetric (anti-symmetric) function of the probe detuning δ = 0. In fact, in the non-resonant case of Δ ≠ 0, the vacuum induced transparency phenomenon still appears even though the corresponding imaginary (real) part of the susceptibility is not symmetric (anti-symmetric), as seen in Fig.  5. The corresponding transparency window appears near δ = Δ , wherein the so-called two-photon resonant condition (ω _p = ω _c) is satisfied.

Fig.  5.

	Figure Option ViewDownloadNew Window
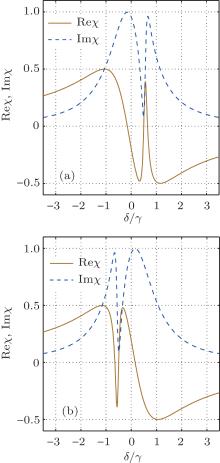	Fig.  5. The real and imaginary parts of the susceptibility as a function of δ for Ng2 = 10κ γ and κ = 0.01γ with (a) Δ = 0.5γ (b) Δ = − 0.5γ .

We note that the EIT-like phenomenon in our system essentially has the same physical origin as the vacuum Rabi splitting (VRS), ^{[22, 24]} i.e., the sharp exchange of energy between two oscillators results in a normal-mode splitting in the eigenvalues, though the original VRS is shown by observing the transmission spectrum of a cavity^{[25, 26]} and our scheme focuses on the probing of the atomic susceptibility. A transparency phenomenon in a system consisting of a two-level atom and a cavity has been studied in Ref.  [27], however the transparency window is not due to the VRS as the atom– cavity coupling is not strong enough. In our scheme, the atom– cavity coupling is collectively enhanced by the number of the atoms, so we can reach the VRS regime relatively easily. To clearly demonstrate this normal-mode splitting, as shown in the profile of Imχ in Figs.  2(b) and 5, we define two new independent bogoliubov modes as follows:

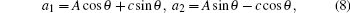
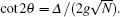
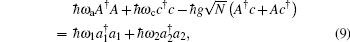
where θ satisfies Then

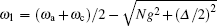
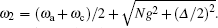
which means that the two coupled modes A (atoms) and c (cavity) split into two independent modes a₁ and a₂ with frequencies and Moreover, from Eq.  (8), we know that the atomic collective mode A just consists of these two dressed modes, i.e. A = a₁ cosθ + a₂ sinθ . As a result, the absorption spectrum Imχ of the atomic ensemble, which is essentially determined by 〈 A〉 , naturally has two peaks located at frequencies ω ₁ and ω ₂ of these two dressed modes. We can see that the coherent features of the atomic ensemble are entirely produced by the atoms– cavity coupling.

As is known, the strong normal dispersion combining with low absorption is particularly suitable for the realization of slow light, which has an extremely small group velocity compared with the velocity of light in a vacuum. In order to calculate the group velocity v_g = c/n_g, we need to compute the group index n_g which is defined as

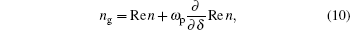
where is the complex index of refraction. For low-density atomic vapors, n ≈ 1 + χ /2, as | χ | ≪ 1. To demonstrate how well we can do, we take a set of parameters for the sodium vapor. As an example, for the 3s→ 3p transition line of the sodium atom, we have ω _a = 2π × 5.09 × 10¹⁴ Hz, γ = 2π × 4.89  MHz, and d = 2.0 × 10^{− 29}  C· m.^{[28, 29]} Under the strong coupling condition Ng² = 10κ γ with a small cavity decay rate κ = 0.01γ and δ = Δ = 0, we find that for low number density N/V = 10¹¹cm^{− 3}, the group index is equal to 6.0 × 10⁵ and v_g = 500.4  m/s. Furthermore, for N/V = 50 × 10¹¹  cm^{− 3}, the group index indeed attains 3.0 × 10⁷, as a result v_g = 10.0  m/s. The results indicate that our scheme is appropriate for realizing slow light.

It has been emphasized that the strong coupling Ng² ⩾ κ γ and the small cavity decay rate κ ≪ γ are the key conditions to trigger the EIT-like phenomenon. Realizing the strong coupling condition is relatively easy, since it can be collectively enhanced by the atom number. The main difficulty lies in the small cavity decay rate, which requires high finesse. Moreover, as shown in Fig.  4(b), a too small κ results in a too narrow transparency window, which may broaden the short probe laser pulse in passing through the atomic ensemble. Alternatively, we can choose other atoms with a relatively large atomic damping rate to realize γ ≫ κ . In addition, as mentioned in Section  3, a large number density can result in a low group velocity. However, we must emphasize that we cannot immoderately enlarge N/V, because it can lead to a remarkable atomic collisional dephasing rate, ^[29] then our method based on the quantum Langevin equations (4) will fail.

The mechanism of VIT in the two-level system can be explained by quantum coherence, which leads to the destructive interference. Initially, the cavity is in the vacuum state | 0_c〉 , and the two-level atomic ensemble is in the ground state | 0_A〉 . When the system is probed by a very weak laser, only three states | 0_A0_c〉 , | 0_A1_c〉 , and | 1_A0_c〉 will be involved. Here | n_Am_c〉 is the Fock state of the two coupled modes, and n_A and m_c are the eigenvalues of A^† A and c^† c, respectively. The combined action of the probing and the controlling fields on the atoms generates quantum coherence between | 0_A0_c〉 and | 0_A1_c〉 (dark state). Then this quantum coherence leads to interference between two absorption pathways, which are | 0_A0_c〉 → | 1_A0_c〉 and | 0_A1_c〉 → | 1_A0_c〉 . Here | 0_A0_c〉 → | 1_A0_c〉 means that the atoms absorb a probing photon with frequency ω _p, and | 0_A1_c〉 → | 1_A0_c〉 means that the atoms absorb a controlling cavity photon with frequency ω _c. When ω _p = ω _c (two-photon resonant condition), the destructive interference between the two absorption pathways results in the transparency. As mentioned above, the high finesse (κ ≪ γ ) and the strong coupling (Ng² ⩾ κ γ ) are the essential conditions to trigger the VIT. On one hand, the cavity decay leads to a dissipative process from | 0_A1_c〉 to | 0_A0_c〉 , which breaks the quantum coherence between | 0_A0_c〉 and | 0_A1_c〉 . On the other hand, the strong coupling gives rise to the quantum coherence. So the decay should be suppressed, whereas the coupling should be enhanced. Here we can see that | 0_A0_c〉 , | 0_A1_c〉 , and | 1_A0_c〉 are analogous to the ground, metastable, and exited states in the EIT, respectively.

The similarity between VIT in the two-level system and the original EIT can also be seen from the corresponding Hamiltonians, which have the similar form of two coupled bosonic modes after defining the atomic collective-excitation modes in these two models. In our model, the quantized cavity field plays the same role as the collective-excitation mode from the ground state to the metastable state in the three-level atomic ensemble. Physically, the additional cavity field (or the additional metastable state) with very small decay rate changes the response spectrum to the probe field which couples with the collective excitation mode from the ground to the excited states.

In conclusion, we have studied the optical response of a two-level atomic ensemble controlled by a high-finesse cavity. We find that the EIT-like coherent phenomenon emerges even when the cavity is in a vacuum. The VIT in our scheme can be regarded as the few-photon case of the CPO, but their mechanisms are in fact different, though the two-level atoms are involved in both models. The former originates from the VRS, while the latter arises from the interference of the controlling and the probing lasers. Note that in the case of CPO, the dip in the imaginary part of the susceptibility does not approach to zero, which means that the transparency is not perfect. Instead, in the present cavity-assisted model, the vacuum induced transparency is near 100% at the two-photon resonant point in the case of a small cavity decay rate. Our scheme also provides another candidate for realizing slow light, which may help promote the quantum computing and optical communications.