Cite this Article
Gao Zhen-Ru†, Zhao Hui-Chang, Yang Li, Wang Feng-Shan. Numerical simulation of the coupling of ultra-wide band electromagnetic pulse into landmine by aperture. Chinese Physics B, 24(9): 094101  
Permissions
Numerical simulation of the coupling of ultra-wide band electromagnetic pulse into landmine by aperture
Gao Zhen-Ru†a),b), Zhao Hui-Changa), Yang Lib), Wang Feng-Shanb)
School of Electronic Engineering and Optoelectronic Technology, Nanjing University of Science and Technology, Nanjing 210094, China
College of Field Engineering, PLA University of Science and Technology, Nanjing 210007, China

†Corresponding author. E-mail: gygzr@sina.com

*Project supported by the Postdoctoral Science Foundation of China (Grant No. 2014M552610).

Abstract

The modern landmine’s electronic fuse is susceptible to strong interference or can even be damaged by the ultra-wide band electromagnetic pulse (UWB-EMP). The finite-difference time-domain (FDTD) method in lossy media with cylindrical coordinates is used to study the interactions of the UWB-EMP with the landmine. First, the coupling of UWB-EMP into the landmine shielding shell through an aperture is numerically simulated. Second, the coupled electromagnetic field of mine shells made of different shielding materials and with apertures of different sizes is plotted. Third, the aperture coupling laws of UWB-EMP into shells are analyzed and categorized. Such an algorithm is capable of effectively preventing ladder similar errors, and consequently improving the calculation precision, and in addition to adopting the message passing interface (MPI) parallel method to divide the total calculating range into more sub-ranges, the overall calculating efficiency is greatly increased. These calculations are surely a constructive reference for modern landmine design against electromagnetic damage.

PACS: 41.20.–q; 41.20.Jb
Keyword: landmine; shielding shell; ultra-wide band; electromagnetic pulse
1. Introduction

The ultra-wide band electromagnetic pulse (UWB-EMP) weapon has witnessed a new concept of radio-frequency directed energy weapons, and many countries have long been in the race for its research and development. As the electromagnetic wave radiation has many unique properties such as a steep rising front edge, high peak-value power, and wide frequency-spectrum range, such new concept weapons are thus capable of strong interference with, or even serious damage of, the electronic as well as electrical system.[1– 4] Most modern mines have applied the electronic fuse technology, for instance, the proximity fuse and time delay fuse, and thus just for its precise and sophisticated structure, such a fuse is susceptible to UWB-EMP interference, under which the fuse either fails to perform its normal function, or turns spuriously detonated or even damaged.[5] Although such shells are made of metal, conductive plastic or other electromagnetic shielding materials that effectively improve the anti-interference capacity against the UWB-EMP, there are often apertures (or slits for manufacturing necessity) on landmine shells as formulated from the annectent devices, and through the aperture coupling operations, the UWB-EMP would easily impose a coupling effect upon the electronic fuse.[6, 7] To improve the capability of resisting UWB-EMP interference, the coupling mechanism as well as the weak segment of EMP in mines ought to be analyzed and understood in terms of a technical experiment or numerical simulation, so as to give a reference for the electromagnetic defense reinforcement. Reference  [8] numerically studied the coupling of UWB-EMP in mines made of plastic shells with rectangular coordinates FDTD, and demonstrated some coupling results of electromagnetic distributions as presented for different incident distances and angles from the antenna to the mine. Reference  [9] calculated the shielding effectiveness of landmine shells made of composite materials on the ideal ground for UWB-EMP with CST electromagnetic simulation software in rectangular coordinates, which are, accordingly, compared with experiment measuring values. All these literatures have provided some references for modern landmine design against the electromagnetic interference.

Most mines are cylindrical in structure, whose surface can be simulated with an FDTD cube grid cell in rectangular coordinates, in which the ladder boundary emerges, driving the transmission of the surface wave and causing numerical dispersion. To improve the calculating precision, the small grid cell dimension is necessary, but the computation quantities increased greatly. To improve the computation efficiency, the HIE-FDTD and HIE-PSTD methods are used to calculate the electromagnetic coupling through slots or apertures.[10, 11] In this paper, the aperture coupling of UWB-EMP into the shielding shell is studied in terms of the FDTD method in the cylindrical coordinates. The coupling regulation of landmine shells made of different shielding materials and with apertures of different sizes is to be analyzed. This algorithm effectively prevents ladder similar errors, and improves calculating precision. Moreover, the total calculating range is divided into many sub-ranges by the MPI parallel method, and the calculating efficiency is greatly improved. The calculating result is thus valuable for modern landmine design against the electromagnetic interference.

2. Numerical analysis method
2.1. Differential equations of FDTD algorithm in cylindrical coordinates

Maxwell’ s equations in cylindrical coordinates are

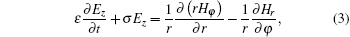
Considering the lossless isotropic and homogeneous medium, the FDTD differential mode of Maxwell’ s equations was established under the cylindrical coordinate system applied with the Yee grid cells. Take the Ez component for example, the differential equation takes the form of

Under the cylindrical coordinates, the spatial step size and time step needs to be more stringent than the Cartesian coordinates. Along the same radial direction, the angle steps are in the same value, while the step phase angle, lateral length of the unit length is different. Therefore, to ensure the convergence of values, the minimum value is required and taken into calculation. Because of the different radial distance among the transverse element length as iΔ r × Δ φ , taking the electric and magnetic fields away from a half space step into account, it is preferable for the grid closest to the axial length of the transverse element, namely, i = 1/2. The stability condition of the time step is

Equation  (7) shows that the differential equation cannot be used at r = 0. Similarly, Hr singularities exist in the axial direction. Ampere’ s law can be used to remove this kind of singularity

Derived from the above equation with a differential equation

where Δ r, Δ φ , and Δ z are the length of grid step along r, circumferential φ , and z in cylindrical coordinates, and Δ t is the time step size.

2.2. CPML absorbing boundary conditions under cylindrical coordinates

The FDTD algorithm requires that Yee’ s grid should be established all within the problem domain space. Due to constraints of computer capacity and calculation efficiency, all calculation should be done in a limited domain, some appropriate absorbing boundary conditions are needed to truncate the open boundary. The PML has proved to be a very valid absorbing boundary condition. However, the absorbing function of the PML absorbing boundary greatly reduces when electromagnetic wave radiation emerges by approaching grazing incidence, and low frequency and lost wave can lead to the false reverberation of the PML boundary. The great reflecting error is produced due to the longer imitated time or the big proportion of low frequency. In order to improve absorbing properties for lost or later low frequency wave, this paper adopts the convolutional perfectly matched layer (CPML) absorbing boundary condition with good absorbing effect, simple format and compliance to the cylindrical coordinates.[12– 15]

Take the Ez component for example, the deduction of the differential equation in the cylindrical coordinates is

where the differential equation of ψ Ezr, ψ Ezrφ , and ψ Ezφ are

where

2.3. MPI parallel FDTD algorithm in cylindrical coordinates

Since any landmine shell aperture is technologically too small, the sub-aperture grid simulation cannot effectively ensure its calculation accuracy. It requires fine mesh, but correspondingly increases the amount of data calculation. To improve the calculating efficiency, the MPI parallel FDTD algorithm is adopted in the cylindrical coordinates. The total area is divided into a plurality of sub-regions, each sub-region corresponds to a process, and through the exchange of data along the process spectrum, calculation of the entire region can be accomplished.[16] Categorized into sub-regions, the connection boundary, absorbing boundary, and scattering body are further divided into some sub-areas, thus increasing the complexity of programming. A variety of methods to achieve the position of the boundary is transmitted to all the sub-domains, sub-domains according to its own grid to determine the scope of the book containing a domain boundary. Various processes at the interface field quantities must communicate with each other to pass through, the amount of which is calculated in flow communication with the field shown in Fig.  1.

Fig.  1. Schematic calculating process and communication.

3. Model building

Usually, the landmines are distributed in the lossy earth. When the UWB-EMP is incident on the landmines, it can couple into the mine by the aperture. The incident UWB-EMP is supposed to be the differential Gaussian pulse,

where E0 is the peak electric field, τ is the pulse width, t0 is the delay time, and the pulse rise time is about τ /4. According to the actual requirements and the radiation characteristics of the Minesweeper antenna, select the peak electric field E0 = 40  kV/m (minesweeper distance of 10  m, the antenna height of 2  m, the pulse source radiation is approximated by a plane wave irradiation), and τ = 2  ns.

To analyze the coupled field inside the landmine, based on some kind of spreading anti-tank mines, let us consider two mine shell materials, hole conditions, and other factors. Five kinds of calculation models are created, as shown in Fig.  2. The structure size and electromagnetic parameters were set as follows.

Fig.  2. Calculation model and locations of sampling points.

Model 1 Mines’ dimensions: height H is 0.13  m, the radius R is 0.053  m. Using an infinitely thin perfect conductor as the mine shell, the shell opens a mine 1  cm× 1  cm holes, pitch Lei shell underside 0.04  m. Placed directly in the lossy earth, h = 0. Electromagnetic parameters of the Earth are taken as σ = 0.01  S/m, ε r = 10.

Model 2 The shell in the mine opened two 1  cm× 1  cm holes, pitch 2  cm, the other parameters are the same as that of Model 1.

Model 3 Ray shell material with a thickness of 0.003  m stainless steel fiber (SSF) filled conductive plastic shielding materials. Based on the lossy flat screen models, test material shielding effectiveness, the measured values are used to fit the equivalent electromagnetic parameters as σ = 30  S/m, ε r = 1.[17] Other parameters are the same as those in Model 1.

Model 4 Hole size of 2  cm× 1  cm, the other parameters are the same as those of Model 3.

Model 5 Lei shell opened two 1  cm× 1  cm holes, pitch 2  cm, and the other parameters are the same as those of Model 3.

To analyze the spatial distribution of the field inside the cavity, we show three samples in the chamber cross section in Fig.  2: the sample section a is a cross section through the hole center, the sample section b is a cross section from 1 cm below the hole, and the sample section c is a longitudinal section through the hole center. In order to analyze the field strength variation in the cavity, the electric field needs to give the time-domain waveform of each component. In cross-section sample a, we take 5 sampling points, a1, a2, a3, a4, a5, respectively, from the axis of 1  mm, 15  mm, 30  mm, 45  mm, 50  mm, also take five sampling points b1, b2, b3, b4, and b5 on the sampling section b.

4. Results and discussion

The internal coupled spatial and temporal distributions of electric and magnetic fields at the sampling points were calculated from Model  1 to Model  5 under the UWB-EMP irradiation conditions.

4.1. Spatial electromagnetic distribution inside mine shells

The spatial electromagnetic distributions from Models  1– 5, on crossing sample sections a, b, and c, are substantially identical at a given time. For example, Model  1 shows various electric field section distributions of sample section b (see Fig.  3) and gives the sampling point’ s time-domain waveform, as shown in Fig.  4. An analysis has shown that the electric field component emerged with a stronger excitation field at the position of the aperture; from the opening position toward the housing, it extends in the radial direction (r direction) of the rapid attenuation of the field strength; and in the axial direction (z direction), the field strength decays with equal pace. The time-domain waveform of Model 1’ s electric field has revealed that the induced electric field was strong at the shell openings, but when it extended within the housing openings, the electric field component decayed fast, the Eφ and Er component decay faster than Ez. Therefore, the mine casing in the layout position of the circuit element ought to avoid the position of the aperture cross section, in particular, the position near the hole.

Fig.  3. Distribution of electric field component. (a) Eφ component; (b) Er component; and (c) Ez component.

Fig.  4. Each sampling point field component time-domain waveform. (a) Eφ component; (b) Er component; (c) Ez component.

4.2. Impact of resonant frequency

UWB-EMP is easy to sew into the landmines through the aperture openings. In such cavities, reflection and refraction form a spatial standing wave form, and the abdominal circuit components in such a standing wave are to be exposed to potentially high electromagnetic fields. The time-domain waveform of each component of the electric field indicated that the electric field Eφ and Er component, internally coupled within infinitely thin metal shell components, witnessed the periodic oscillation after a stable waveform oscillation, and its oscillation period is approximately 1.7  ns. The electric field Eφ and Er components within shielding composite material shells equally witnessed the periodic oscillation after a stable waveform oscillation, and its oscillation period is approximately 1.8  ns. The approximate resonant frequency, which can be calculated from the resonance period, is respectively 5.8 × 108  Hz for infinitely thin metal casing, and 5.6 × 108  Hz for the composite materials of the lightning shields. Therefore, the operating frequency of the circuit components should avoid a choice close to the resonant frequency, because such a frequency that is close to the resonant frequency of the electromagnetic field coupling is strong, which is thus possible to make permanent damages to the electronics, or has a liability of fuse malfunction, spurious detonation, or surface breakdown.[18]

4.3. Comparison of inside field enhancement of landmine with different materials

Seen from the peak value of each component electric field, the internal coupling field strength in mines made of composite shielding materials is higher than that of mines made of metal shells. Table  1 lists the peak values of the coupling electric field component in mines made of different shell materials under different cavities. Regarding apertures of the same size and with the same position, the internal coupling Eφ component in mines of composite shielding materials is about 20 times higher than that in mines of metal shells; the field strength Er component is about 10 times higher; and the field strength Ez component is about 3 times higher. For resisting anti-landmine destruction of UWB-EMP interference ability, it is recommended that the existing composite shielding materials are coated with thin metallic coating so as to achieve a better shielding effect.

Table 1. Peak value of the coupling electric field in sample section b.
4.4. Impact of different sizes of apertures upon the coupling fields

The internal coupling fields within the shielding shells of composite materials under 1  cm× 1  cm and 2  cm× 1  cm circumstances have been calculated. Judging from the calculation results (Table  1), the electric field induced at openings is evidently higher than that in the internal coupling within larger sizes, but the coupled electric field away from the opening shows no essential difference either within small or larger sizes, and there are only about 2 times difference of the Er component. Thus, it is necessary to conscientiously design aperture size and location according to practical requirements.

5. Conclusion

To analyze the coupling problem of UWB-EMP and landmines by the numerical approach, this paper applies the cylindrical coordinate parallel FDTD algorithm and CPML absorbing boundary conditions, presents numerical simulation results of the aperture coupling effect of cylindrical shell mines made of two electromagnetic shielding materials, and demonstrates their respective time-domain waveforms of the coupling electromagnetic field and its electric field component in shells of different shielding materials and apertures with different sizes.

With an analysis of the aperture coupling laws of UWB-EMP in mine shells made of ideal metal conductors and conductive plastic landmines, and together with an analysis of the coupled resonant frequency as well as the impact of aperture size, this paper has also proposed some suggestions for designing shell structures against the UWB-EMP interference and damage.

Reference
1 Li C L 1999New Concept Weapons Beijing National Defense Industry Press p.  56 (in Chinese) [Cited within:1]
2 Zhou B H, Chen B and Gao C 2002 Microwave Journal 18 88(in Chinese) [Cited within:1]
3 Zhang S Q 2012 Chin. Phys. B 21 065101 DOI:10.1088/1674-1056/21/6/065101 [Cited within:1]
4 Yang H J, Li W K and Li F 2013 Aerospace Electronic Warfare 29 15(in Chinese) [Cited within:1]
5 Li G, Bi J J, Liu S H and Sun Y W 2006 High Power Laser and Particle Beams 18 1332(in Chinese) [Cited within:1]
6 Xiao J S, Liu W H, Zhang S Y and Zang J H 2010 High Power Laser and Particle Beams 22 2959(in Chinese) DOI:10.3788/HPLPB [Cited within:1]
7 Wang J G, Liu G Z and Zhou J S 2003 High Power Laser and Particle Beams 15 1093(in Chinese) [Cited within:1]
8 Luo G X, Meng F X, Tong C J and Wang J G 2003 High Power Laser and Particle Beams 15 805(in Chinese) [Cited within:1]
9 Luo X N, Fang X, Gao Z R, Liu J and Fang K 2013 Journal of Metallic Functional Materials 44 2276(in Chinese) [Cited within:1]
10 Chen J and Wang J 2007 IEEE Trans. Electromagn. Compatibility 49 354 DOI:10.1109/TEMC.2007.893329 [Cited within:1]
11 Chen J and Wang J 2013 IEEE Trans. Electromagn. Compatibility 55 1239 DOI:10.1109/TEMC.2013.2265037 [Cited within:1]
12 Huang J L, Yao L J and Shen T 2013 IEEE Transactions on Electromagnetic Compatibility 55 1187 DOI:10.1109/TEMC.2013.2257795 [Cited within:1]
13 Wang J G, Wang Y and Zhang D H 2006 IEEE Transactions on Plasma Science 34 681 DOI:10.1109/TPS.2006.875830 [Cited within:1]
14 Wang Y G, Chen B and Chen H L 2014 IEEE Antennas and Wireless Propagation Letters 13 714 DOI:10.1109/LAWP.2014.2315435 [Cited within:1]
15 Wang Y, Wang J and Chen Z 2015 Chin. Phys. B 24 024101 DOI:10.1088/1674-1056/24/2/024101 [Cited within:1]
16 Qi G L, Hu H, Zhou D F, Hou D T and Zhang C 2010 J. Microw. 26 19(in Chinese) [Cited within:1]
17 Niu S, Jiao C Q and Li L 2013 Acta Phys. Sin. 62 214102(in Chinese) DOI:10.7498/aps.62.214102 [Cited within:1]
18 Wang J, Cai L, Zhu X, Wang Y and Xuan C 2010 Phys. Plasmas 17 063503 DOI:10.1063/1.3432715 [Cited within:1]