†Corresponding author. E-mail: dajund@jlu.edu.cn
*Project supported by the National Basic Research Program of China (Grant No. 2013CB922200) and the National Natural Science Foundation of China (Grant Nos. 11034003 and 11127403).
The tunneling ionization rates of vibrationally excited N2 molecules at the ground electronic state are calculated using molecular orbital Ammosov–Delone–Krainov theory considering R-dependence. The results show that molecular alignment significantly affects the ionization rate, as the rate is mainly determined by the electron density distribution of the highest occupied molecular orbital. The present work indicates that the ratios of alignment-dependent rates of different vibrational levels to that of the vibrational ground level increase for the aligned N2 at the angle θ = 0°, and suggests that the alignment-dependent tunneling ionization rates can be used as a diagnostics for the influence of vibrational excitation on the strong field ionization of molecules.
Strong field ionization of molecules is of interest in many areas of physics and chemistry, particularly as it applies to optical techniques, such as high harmonic generation or pulse generation, orbital tomography, and structure determination. Molecules can be ionized by optical fields delivered by a pulsed laser through multi-photon ionization, [1, 2] above-threshold ionization, [3] or even tunneling ionization, [4] depending on field intensity. Compared to the ionization of atoms, the ionization of molecules is a complex many-body problem due to molecular nuclear motion, even for the most simple molecule or under the single active electron (SAE) approximation.[5– 8] Various theoretical methods using, for instance, Ammosov– Delone– Krainov (ADK) theory, [9, 10] molecular orbital Ammosov– Delone– Krainov (MO-ADK) theory, [4, 11] Keldysh– Faisal– Reiss (KFR) theory, [12, 13] the three-dimensional Schrodinger equation, [14, 15] and spin-flip density functional theory, [16] have successfully illustrated strong field ionization phenomena. In principal, in intense laser fields, molecules can be excited both electronically and vibrationally. The theoretical treatment of the influence of vibrational excitation on strong field ionization is complicated and difficult, and the models used must be verified. Furthermore, as ionization rates of molecules in the tunneling regime critically depend on the molecular ionization potential, i.e., the difference in the neutral and ion electronic potentials of the molecule, a simple way to include the vibrational influence is to approximate the vertical ionization potential as the change in vibrational amplitude, Δ V(R).[4, 17] This method has been used to identify the enhancement of ionization due to initial vibrational levels of H2, N2, and CO2 molecules, and illustrate the importance of vibrational motion.[18] However, because electronic and nuclear motions occur at different time scales, these previous studies have shown that the vibrational influence on ionization of molecules is not obvious, except in the case of H2. Several studies have demonstrated that the influence of molecular orientation on ionization rates is significant compared to the vibrational effect, i.e., N2 molecules are four times more likely to ionize when aligned parallel to the field than when aligned perpendicular to it.[6, 19]
In the present work, we theoretically study the vibrational effects on strong field ionization of molecules by investigating the tunneling ionization rates of aligned molecules of different vibrational excited levels in the ground electronic state. The alignment-dependence of the rates are calculated using molecular orbital MO-ADK theory, which is a simple, efficient approach to give practical comparisons for experimentalists.[6] To obtain a more accurate ionization potential Δ V(R) for use in ionization rate calculations, Coupled-cluster singles doubles and non-iterative triples correction (CCSD(T)) potentials are calculated. Ionization dependence on alignment given different vibrational levels exhibits characteristics that follow the electron density distribution of the highest occupied molecular orbital (HOMO) and indicate the enhancing effect of vibrational excitation on ionization of aligned molecules. Our study suggests a new approach to further explore the vibrational effect on the strong field ionization of molecules.
We use the MO-ADK theory, developed by Tong, Zhao, and Lin[4] based on the SAE approximation, in this work. To describe the aligned molecular ionization in intense laser fields, we choose a space-fixed frame and a molecular frame, with coordinates (X, Y, Z) and (x, y, z), respectively, and the laser polarization direction and the molecular axis are set as the Z and z axes, accordingly. The asymptotic wave function of a valence electron at a large distance is expressed as

where l is the angular momentum quantum number and m is the magnetic quantum number along the molecular axis, Cl is the structural parameter of molecule, atomic units m = ℏ = e = 1 are used, and the radial wave function is expressed as
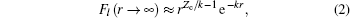
with effective Coulomb charge Zc, 

with
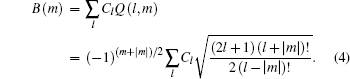
The ionization rate using the adiabatic approximation is given by[3]
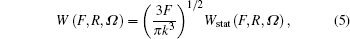
where Ω = Ω (φ , θ , χ ) is the Euler angle, θ is the molecule orientation angle, representing the angle between the laser polarization and the molecular axis, R is the nuclear distance, and static ionization rate

Assuming laser polarization along the z axis in polar coordinates, the alignment-dependent tunneling ionization rates of molecules, with a fixed nuclear distance R, can be obtained from Eq. (5) using structural coefficients Cl. Thus, the ionization rate of a given vibrational level and orientation angle θ is

where υ is the vibrational quantum number, and the vibrational wave function Ψ υ , obtained by solving the radial Schrö dinger equation used in LEVEL, [20] determines the probability distribution of R. Then, the average value of the ionization rate for vibration over all orientation angles θ is expressed as[6]

where integration over θ from 0 to π /2 is sufficient due to the symmetry of the N2 molecules.
We use simple N2 molecules as models to study complicated vibration effects. The molecular orbitals of different vibrational levels in the ground electronic state are calculated using the Hartree– Fock (HF) method in GAMESS code, with the basis set ACC5 and including electron correlation. Using the HF wave-function fitting method, [21] we obtain the molecular orbital coefficients Cl at the ground electronic state by matching these functions to the form in Eq. (2). Our Cl are listed in Table 1, together with those from previous studies.[4, 6, 21, 22] Tong et al.[4] obtained the coefficients Cl using a multiple scattering method. Kjeldsen later calculated the Cl using the more accurate HF wave function fitting method.[21] The coefficients Cl obtained by Chu et al. using the density functional theory (DFT) method[6] are similar to those from Kjeldsen’ s HF calculations. In order to improve the wave function with correct asymptotic behavior, Zhao et al.[22, 23] proposed a method of obtaining Cl by solving the time-independent Schrö dinger equation including the electronic exchange– correlation potential. Their calculated tunneling ionization probabilities are in good agreement with most experimental data and with most theoretical calculations for linear molecules. While we calculate Cl by a procedure similar to Kjeldsen’ s method, [21] we use a more accurate ACC basis and include the electronic exchange– correlation potential, so our coefficients are closer to those of Zhao.[22] This indicates the importance of asymptotic wave functions and electronic correlation in the simple MO-ADK method. The Cl calculated for different nuclear distances of N2 are also listed in Table 2 for reference, since no such data exists in the literature.
| Table 1. Molecular structural coefficients Cl of N2 in the ground electronic state calculated using our MO-ADK method and published by others previously (Kjeldsen et al.[21] HF, Chu et al.[6] DFT, Tong et al.[4] and Zhao et al.[22] MO-ADK). |
| Table 2. Molecular structural coefficients Cl of N2 at different nuclear distances. |
In order to calculate the ionization rates, it is crucial to obtain accurate data of molecular potential energy curves because the rates are very strongly dependent on the ionization potential, in MO-ADK theory, as in Eq. (4). In most cases, the ionization potential of electrons in the molecular ground state varies with internuclear distance, since the neutral and ionized molecular potential curves are different. The molecular potential energy curves required can be obtained by ab initio quantum calculations. The CCSD(T)/aug-cc- pV5z-DK method is used to calculate the ground potential energy curves of 




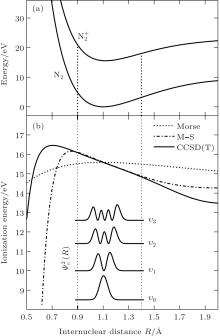
We reexamine the total tunneling ionization rate of N2 molecules obtained by MO-ADK from Eq. (8), and compare it with previously published results based on atomic ADK[17] and MO-ADK[27, 28] as well as experimental measurements in Fig. 2.[29] Agreement of our calculations with previous theory and experiment indicates the validity of the present method. The slight discrepancies are likely to be due to the different potential curves used. For example, the ionization energy from CCSD(T) curves differs from that of Morse potential curves, even in range near Re, as shown in Fig. 1(b), which leads to a larger ionization rate in the present work than in Saenz’ s paper, [17] in which they applied ionization energy with various nuclear distances to ADK. Our calculated total rate is consistent with those of Gallup[27] and Zhang, [28] which used the same MO-ADK framework, but with slightly different single-electron wave functions and ionization energies, calculated as the Hartree– Fock levels using the theory from GAMESS.[30] The basis set aug-cc-pVTZ and 6-311G (s, p, d) were used by Zhang[28] and Gallup, [27] respectively, while we used the aug-cc-pV5Z basis set here. Our calculations are in agreement with ab initio KFR results, [12] although the results deviate from quantum calculations reported previously.[6]
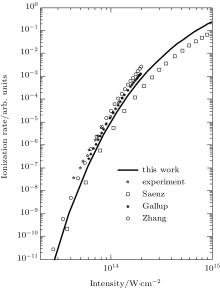 | Fig. 2. The ionization rate of molecular N2 in strong laser fields calculated from MO-ADK (this work), ADK (Saenz[17]), and MO-ADK (Gallup[27], Zhang[28]). Experiment results (Guo[29]) are also shown. |
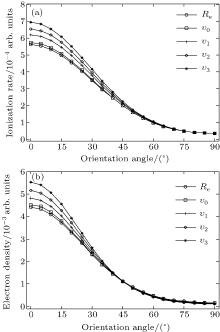
Furthermore, we calculate the ionization rates using Eq. (5) for different vibrational levels with nuclear distances R ranging from 0.9 Å to 1.4 Å in 0.01 Å increments, and orientation angles θ ranging from 0 to 90° at a laser intensity of 1.5 × 1014 W/cm2 (Keldysh parameter γ = 0.93, [31] in the tunneling ionization region for λ = 800 nm). The alignment-dependent tunneling ionization rate is shown in Fig. 3. The alignment effect of N2 is important to tunneling ionization, as reported previously.[19] Because the molecular orbital symmetry of N2 in its ground state is σ g, the electrons distribute along the molecular axis and are more easily ionized when the molecular axis is parallel to the polarization direction of the laser pulses.[32] These results agree with observations that the rate is larger as N2 aligns to the laser polarization direction, while the rate is minimal for N2 perpendicular to the laser polarization direction. For the same orientation angle, the ionization rate increases with increasing internuclear distance R, because the ionization energy decreases, as shown in Fig. 1(b). Compared to the ionization rate at the equilibrium nuclear distance Re for all orientation angles, the ionization rates at different nuclear distances R are much greater at small orientation angles, especially at θ = 0° . Therefore, due to the enlargement of the region for molecular nuclear motion, a large distribution of R in molecular vibrational excitation should enhance the tunneling ionization. This effect can be seen more clearly at smaller orientation angles θ for a given internuclear distance R when considering the alignment dependence of the ionization rate from different vibrational levels.
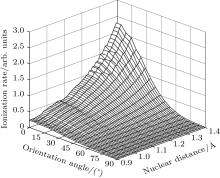 | Fig. 3. Alignment-dependent tunneling ionization rates of different nuclear distances R with a laser intensity of 1.5 × 1014 W/cm2 and wavelength of 800 nm. |
We calculate the alignment-dependent ionization rates of N2 in the ground electronic state (σ g) alone and including individual vibrational states (ν 0, ν 1, ν 2, and ν 3) (see Fig. 4(a)). Firstly, for all vibrational states, the ionization rates have maxima when N2 is aligned to the laser polarization direction and minima when N2 is perpendicular to the laser polarization direction, similar to ionization rates of N2 in its ground electronic state. This indicates that the alignment dependence is mainly determined by the molecular symmetry of the HOMO electronic state (σ g), as predicted by previous MO-ADK calculations.[33] Secondly, we note that, generally, the ionization rates are increased for excited vibrational levels υ n (n = 1, 2, 3), compared to the ground vibrational level υ 0, due to decreasing ionization potentials. Moreover, the alignment dependence of this vibrational enhancement for different vibrational levels can be interpreted from the electron density population in the vibrational level (see Fig. 4(b)), obtained from
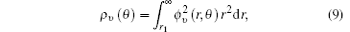
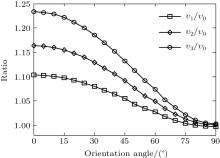
where φ υ is the vibrational wave function of the electron from HF, r is the region ionized for electrons, and r1 is around 5 a.u. By comparing Figs. 4(a) and 4(b) it can be seen that the electron density distribution and the alignment-dependent tunneling ionization rates share the same tendencies for different υ n levels, indicating that alignment dependence reflects properties of the molecular orbitals. Figure 5 gives the ratios of the orientation-dependent ionization rate of the different excited vibrational levels to that of the vibrational ground level. The data indicate that the ratios increase with alignment of N2 (at orientation angle θ = 0° ). Therefore, we conclude that measurements of the alignment-dependent ionization rate combined with simple MO-ADK calculations could be diagnostic of the influence of vibrational excitations on tunneling ionization, even for molecules with vibrational level-independent total ionization rates, such as N2.[18]
We studied the alignment-dependent ionization rates of N2 molecules at different vibrational levels in their ground electronic state using MO-ADK theory with consideration of R-dependence. Using the accurate ionization potential Δ V(R) from the CCSD(T) potential energy curves of the ground states 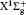


Discussions about the calculations with Prof. Zengxiu Zhao and Dr. Bin Zhang are acknowledged.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|