†Corresponding author. E-mail: jiqingch@hebut.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 90403007 and 10975044), the Key Subject Construction Project of Hebei Provincial Universities, China, the Research Project of Hebei Education Department, China (Grant Nos. Z2012067 and Z2011133), the National Natural Science Foundation of China (Grant No. 11147103), and the Open Project Program of State Key Laboratory of Theoretical Physics, Institute of Theoretical Physics, Chinese Academy of Sciences, China (Grant No. Y5KF211CJ1).
Covalent bonds arise from the overlap of the electronic clouds in the internucleus region, which is a pure quantum effect and cannot be obtained in any classical way. If the intermolecular interaction is of covalent character, the result from direct applications of classical simulation methods to the molecular system would be questionable. Here, we analyze the special intermolecular interaction between two NO molecules based on quantum chemical calculation. This weak intermolecular interaction, which is of covalent character, is responsible for the formation of the NO dimer, (NO)2, in its most stable conformation, a cis conformation. The natural bond orbital (NBO) analysis gives an intuitive illustration of the formation of the dimer bonding and antibonding orbitals concomitant with the breaking of the π bonds with bond order 0.5 of the monomers. The dimer bonding is counteracted by partially filling the antibonding dimer orbital and the repulsion between those fully or nearly fully occupied nonbonding dimer orbitals that make the dimer binding rather weak. The direct molecular mechanics (MM) calculation with the UFF force fields predicts a trans conformation as the most stable state, which contradicts the result of quantum mechanics (QM). The lesson from the investigation of this special system is that for the case where intermolecular interaction is of covalent character, a specific modification of the force fields of the molecular simulation method is necessary.
The molecular behavior is in principle indicated by quantum mechanical laws. The chemical bonds, molecular charge distributions, molecular vibrational frequencies, intermolecular interactions and many other quantities can be calculated by solving quantum many-body equations. When the number of the atoms of a molecular system is more than hundreds of thousands, the QM calculation cannot be practically accomplished and many approximate methods were developed, in which how to appropriately describe those intermolecular interactions is a crucial question. The molecular dynamics method is a well developed and widely used method for the investigation of molecular systems consisting of large number of atoms. In this method those relevant quantities and interactions are approximately described by introducing a set of parameters and effective potentials (i.e., the force fields) and then the mechanical behavior of molecules is indicated by classical mechanics principles.[1] The intermolecular interactions, for instance, are expressed by both Coulomb potentials and van der Waals (VDW) potentials, which can really give a good approximation of the funnel-like potential obtained by QM calculation for most practical cases. The direct application of the Coulomb potential results in those polar interactions, e.g., hydrogen bonding, being described to a good extent by the classical approximation. However, in quantum mechanics the Coulomb potential is just an operator appearing in the Hamiltonian of the system. When the exchange force is important for the interacting partners (as in the case of a covalent bond between two atoms), the real interaction between them can never be approximated just by polar interaction.[2] The exchange force arises from the overlap of the electronic clouds which is a pure quantum effect. When intermolecular interaction has such a typical quantum character, the behavior of the corresponding molecular system cannot be properly described using classical molecular simulation methods.
The intermolecular interactions with covalent feature are rarely encountered. Here, we provide an important archetype of NO dimer and analyze the origin and character of its special covalent intermolecular interaction. With a singly-occupied highest-occupied molecular orbital (HOMO), the NO molecule is a radical. It has a weak dipole moment (∼ 0.2857 D, according to our calculation) due to the difference between the electronegativities of N and O atoms. Intuitively, when two NO molecules interact with each other, their stable conformation should be a trans conformation with their dipole moments being antiparallel. However, lots of theoretical and experimental investigations revealed that the most stable conformation of the NO dimer is a cis conformation, cis-ONNO (1A1) (Fig. 1), which is formed via a special covalent intermolecular interaction arising from the bonding between the two singly occupied π * molecular orbitals (MOs) of the two NO monomers.[3– 13] This intermolecular interaction is very weak with a binding energy of ∼ 8.3 kJ/mol, even though it is a typical covalent bond. As more and more sophisticated methods were applied, more and more quantum structures of the metastable states of the NO dimer have been unraveled, [14– 17] which largely deepen and widen the knowledge of intermolecular interactions. However, why the special intermolecular interaction of the NO dimer is so weak still needs a satisfactory explanation.
Early in 1981, Ha pointed out that “ the attractive forces due to the bonding between the singly occupied π * MOs of NO are counteracted by strongly repulsive forces arising from the overlap of fully occupied π MOs.” [8] This viewpoint confirmed one of the counteracting factors to the dimer bonding but it has two problems. First, the NO monomers have other fully occupied MOs which should also contribute to the counteraction. Second, since the two singly occupied π * MOs of the two NO monomers form the bonding dimer orbital, the other monomer orbitals should also form dimer orbitals and the repulsive force should arise from the effective charge distribution of all the dimer orbitals. Gonzalez-Luque et al. analyzed the ground state conformation of the NO dimer using a multi-reference configuration interaction method and calculated the occupation numbers of the natural orbitals with the coupled pair functional (CPF) method.[9] Their results showed that the CPF bonding orbital σ NN and antibonding orbital 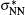
In this work, we optimized the NO dimer structure with coupled cluster singles and doubles (CCSD) method and obtained relevant geometric parameters in good agreement with the experiment. Furthermore, the MO and natural bond orbital (NBO) analysis were performed to understand the formation mechanism of the special weak intermolecular interaction. The MO analysis shows that the special dimer covalent bond is formed by two unpaired π * electrons of the two monomers. Those fully occupied monomer orbitals also combine to form dimer orbitals in pairs with one bonding dimer orbital and one antibonding dimer orbital. Since the antibonding interactions are more destabilizing than bonding interactions are stabilizing, [25] the net effect of these dimer orbitals does not favor the binding of the dimer. But it is difficult to see this counteracting effect directly from the dimer orbitals. We then perform an NBO analysis. The NBO method is good at describing the effective charge distribution and charge transfer.[18, 19] The NBO analysis of the NO dimer reveals that a large-scale charge redistribution occurs concomitantly with the formation of the NO dimer. For comparison, we also perform an optimizing calculation for the conformation of two NO molecules by directly applying molecular mechanics (MM) method with the UFF force field.
The organization of the rest of this paper is as follows. In Section 2, the simulation method and parameters used in this work are briefly described. Section 3 presents the calculation results and the related analysis of the NO monomer and dimer by the MO method, the NBO method, and the MM method, respectively. The conclusions are given in Section 4.
The ground state of cis-ONNO (1A1) with C2v symmetry was optimized with the CCSD method at 6-31+ G* level. Since the aim of this work is to give an intuitive analysis for the formation mechanism and bonding character of the NO dimer in the ground state, we did not use a high accuracy method with a large basis set. Those works with accurate computational details can be found in the references.[1– 13] The frequency calculation was carried out to confirm the structure as the minimum point in energy. The structure parameters and the binding energy were calculated for the optimized structure with the basis set superposition error (BSSE) correction.[20] The NBO analysis was performed for both the monomer and the dimer. The quantum calculations were performed using the Gaussian03 program.[21] The MM optimization for the dimer was finished with UFF force field.[22] The VMD (visual molecular dynamics) program is employed for the molecule visualization and the production of molecular orbital plots.[23]
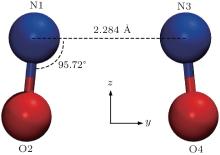
The optimized geometry of the ground state NO dimer obtained at the CCSD/6-31+ G* level is depicted in Fig. 1. As seen, the NO dimer in the ground state has a coplanar structure with C2v symmetry, denoted as cis-ONNO (1A1). The distance between the two nitrogen atoms RNN (∼ 2.281 Å ) is larger than the length of a typical chemical bond (∼ 1 Å ) and less than the sum of VDW radii of two nitrogen atoms (3.10 Å ), [24] indicating that there is a definite intermolecular interaction between the two monomers.
The optimized geometry parameters of the ground state NO dimer obtained by theory and experiment are listed in Table 1, where the values of this work are also given for comparison. It is seen that our present optimized results are in good agreement with experimental ones and our following analysis is based on these results.
| Table 1. The optimized structure parameters of cis-ONNO (1A1) by theory and experiment. |
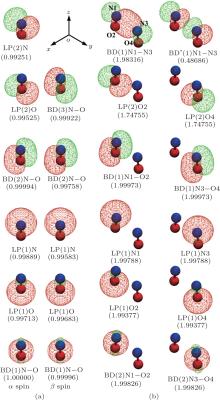
In order to get an intuitive understanding for the formation mechanism and bonding character of the NO dimer in the ground state, the orbitals of the optimized ground state NO dimer were calculated at the CCSD/6-31+ G* level. The results of those relevant dimer orbitals are selected and shown in Fig. 2. As seen, the HOMO of the NO dimer is the fully occupied bonding orbital arising from the head-to-head overlap of the singly occupied π * MOs of the two NO monomers. This is the typical way of forming a covalent σ bond. This covalent intermolecular interaction is responsible for the geometry of the cis conformation of the NO dimer in the ground state.
An important structural feature of the NO dimer is the distance between the two monomers (see Fig. 1 and Table 1). The distance, 2.281 Å , is approximately twice the length of a typical chemical bond, and correspondingly the binding energy of the NO dimer (∼ 8.3 kJ/mol) is much smaller than that of a typical chemical bond, even though the dimer σ bond is fully occupied. These facts indicate that there must be strong repulsive forces between the two monomers which counteract the attractive force of the dimer σ bond, otherwise a fully occupied σ bond should contribute a binding energy of several electron volts (eV). The repulsive forces should arise from the electrons other than that in the HOMO bonding orbital. Besides the HOMO σ bond, the dimer has another ten dimer orbitals in the valence shell formed from the monomer’ s fully occupied MOs (Fig. 2). The ten dimer orbitals appear in pairs with fully occupied bonding orbitals and antibonding orbitals. Since the antibonding orbital is more antibonding than the bonding orbital is bonding, [25] the net effect of these dimer orbitals does not favor the binding of the dimer. This is the counteracting factor to the dimer σ bond that makes the special intermolecular interaction of the NO dimer rather weak. In Fig. 2, we do not denote the energy for each dimer orbital. As is well known, the sum of the orbital energy is not equal to the total energy of the system and it is difficult to calculate the net contribution from each pair of bonding– antibonding orbitals.[26] The counteraction should arise from the effective charge distribution which cannot be seen directly from those dimer orbitals, we thus perform a NBO analysis of the NO dimer.
As is well known, a chemical reaction is accomplished through breaking the old bonds and forming the new bonds with the total number of the bond orders of the reactants and products unchanged. The charge transfer and redistribution during this process is effectively described by the NBO method.[18, 19] Generally speaking, intermolecular interactions differ from chemical bonds in that no phenomena of chemical bonds breaking and forming or evident charge redistribution take place before and after the interactions. However, in the special case of the ground state NO dimer the phenomena do occur as shown in the following NBO analysis. The valence-shell natural bond orbitals with high occupancies of both NO monomer and dimer are depicted in Fig. 3, where the orbitals of the monomer with different spins are shown in two columns separately. The top three NBOs in Fig. 3(a) show the effective distribution of the charges responsible for the three-electron π bond of the NO monomer. It is seen that the 0.5 bond order of the π bond is effectively achieved through the singly occupied π bond (BD(3)O– N, β spin) and the other two electrons of the three electrons are distributed in the two lone pair orbitals (LP(2)N and LP(2)O), respectively. Upon formation of the NO dimer, the distribution of the three charges in the three monomer NBOs is largely changed and, most strikingly, the two singly occupied π bonds of the two monomers are broken, as seen in Fig. 3(b). The NBOs of the NO dimer are shown in Fig. 3(b) with the occupancies denoted in the parentheses.It is clearly seen that there is only one dimer bond (BD(1)N1– N3) which is formed through the overlap of the two LP(2)N orbitals of the monomers. This is a typical covalent σ bond with occupancies of ∼ 2. The attracting force from this covalent bond is responsible for the formation of the NO dimer but it has two counteracting factors. As seen in Fig. 3(b), the singly occupied π bonds of the two monomers are broken upon the dimer formation. The two charges are redistributed into three dimer NBOs, i.e., LP(2)O2, LP(2)O4, BD* (1)N1– N3. The first two orbitals share ∼ 1.5 charges equally and the third orbital obtains ∼ 0.5 charges. The third orbital, BD* (1)N1– N3, is a dimer antibonding orbital. Filling charges into this antibonding orbital must weaken the dimer binding. This is the first counteracting factor to the dimer σ bond. The second counteracting factor arises from the repulsion between those fully or nearly fully occupied nonbonding orbitals. The intermolecular distance of the NO dimer in the ground state is 2.281 Å (Fig. 1). Within this distance those fully or nearly fully occupied nonbonding NBOs in pairs must overlap and therefore produce repulsion between them. This is the second counteracting factor to the dimer σ bond. Effectively, the contribution of these two counteracting factors is close to the strength of the dimer σ bond that makes the total binding strength of the NO dimer rather weak.
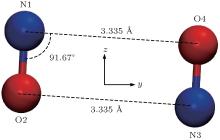
The covalent binding of the NO dimer in the ground state is a special intermolecular interaction which is of pure quantum characters. If one wants to perform an MD simulation on a system consisting of NO molecules, one must use some force field and ascribe charges to each atom. To see whether a NO system could be described properly by a classical method, we optimized the conformation of two NO molecules using molecular mechanics (MM) method with UFF force field.[22] The resulting optimized structure for two NO molecules is shown in Fig. 4. As seen, a trans conformation is the most stable structure of two NO molecules using MM method. The intermolecular distance RN1-O4 (3.335 Å ) is close to the sum of the VDW radii of N and O atoms.[24] The binding energy obtained by MM method for the two NO molecules with a trans conformation is 3.11 kJ/mol which is only a little higher than the thermal energy at ambient condition (∼ 2.5 kJ/mol). The optimized conformation of two NO molecules by MM method should appear with a high probability in a molecular dynamics simulation of the NO system. However, as revealed by both quantum mechanical calculation and experimental investigations, the most stable conformation of two NO molecules with a high appearing probability in the gas-phase or condensed-phase NO system is a cis (1A1) structure, indicating that the direct classical mechanics simulation of a NO system with ordinary force fields cannot give a correct description for this special molecular system.
The CCSD/6-31+ G* calculation for the NO dimer reveals a parallel (cis) conformation in its ground state. The attracting force responsible for the formation of the dimer is a covalent intermolecular interaction which is achieved through the overlap of two singly occupied monomer orbitals in a head-to-head manner, meaning that it is a typical σ bond. Binding through a σ bond should be strong but this intermolecular σ bond is practically rather weak. The NBO analysis reveals that upon formation of the dimer σ bond, two monomer π bonds (each with bond order 0.5) are broken and the two charges are redistributed into three dimer orbitals. The antibonding dimer orbital obtains ∼ 0.5 of the two charges and two nonbonding dimer orbitals share the remaining charges. Filling charges into antibonding orbital produces the first counteracting factor to the dimer bonding. The second counteracting factor comes from the overlap of the nonbonding dimer orbitals in between the two monomers. Because these nonbonding dimer orbitals are fully or nearly fully occupied and the intermolecular distance is smaller than the sum of the VDW radii of the atoms, there is a strong repulsion among the charges distributed in these orbitals. The formation of the covalent dimer σ bond concomitant with the breaking of the monomer π bonds is a phenomenon that is common to chemical reactions but uncommon to intermolecular interactions. The MM optimizing calculation for the NO dimer with UFF force fields predicts an antiparallel (trans) conformation which is in conflict with the results from quantum mechanical calculation and experiment, suggesting that the typical quantum mechanical process cannot be described by classical simulation method. The lesson from the investigation of this special system is that for the case where intermolecular interaction is of covalent character, the force fields must be properly modified when simulating the corresponding molecular system with classical simulation method. Since two NO molecules have other metastable binding states with binding energies differing from the ground state energy only by several kJ/mol, as revealed by the high accuracy quantum chemical calculations, [3– 17] the modification of the force fields for the MD simulation of the NO molecular system would be a challenge.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|