Cite this Article
Gao Shi-Gen, Dong Hai-Rong†, Ning Bin, Roberts Clive, Chen Lei, Sun Xu-Bin. Cooperative adaptive bidirectional control of a train platoon for efficient utility and string stability. Chinese Physics B, 24(9): 090506  
Permissions
Cooperative adaptive bidirectional control of a train platoon for efficient utility and string stability
Gao Shi-Gena), Dong Hai-Rong†a), Ning Bina), Roberts Cliveb), Chen Leib), Sun Xu-Binc)
State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China
Birmingham Centre for Railway Research and Education, School of Electronic, Electrical and Systems Engineering, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044, China

†Corresponding author. E-mail: hrdong@bjtu.edu.cn

*Project supported by the Beijing Jiaotong University Research Program, China (Grant No. RCS2014ZT18), the Fundamental Research Funds for Central Universities, China (Grant No. 2015JBZ007), and the National Natural Science Foundation of China (Grant Nos. 61233001, 61322307, and 61304196).

Abstract

This paper proposes cooperative adaptive control schemes for a train platoon to improve efficient utility and guarantee string stability. The control schemes are developed based on a bidirectional strategy, i.e., the information of proximal (preceding and following) trains is used in the controller design. Based on available proximal information (prox-info) of location, speed, and acceleration, a direct adaptive control is designed to maintain the tracking interval at the minimum safe distance. Based on available prox-info of location, an observer-based adaptive control is designed to achieve the same target, which alleviates the requirements of equipped sensors to measure prox-info of speed and acceleration. The developed schemes are capable of on-line estimating of the unknown system parameters and stabilizing the closed-loop system, the string stability of train platoon is guaranteed on the basis of Lyapunov stability theorem. Numerical simulation results are presented to verify the effectiveness of the proposed control laws.

PACS: 05.60.–k; 07.05.Dz
Keyword: train platoon; string stability; cooperative adaptive control; efficient utility
1. Introduction

Train tracking interval control is one of the main tasks of the automatic train protection (ATP) system in current train operation signaling systems.[1] With the purpose of maximizing the railway traffic volume, it is necessary to calculate the minimum real-time tracking interval and maintain the minimum safe distance between two trains. With the help of modern communication-based train control (CBTC) systems, [2– 4] the “ moving block” principle can be implemented using information of the real-time train speed, track geometry, direction of movement, required safe braking distances, and stopping characteristics, which allows the tracking point of a train to be the rear of preceding train (plus a necessary safety allowance) instead of an entrance point of a fixed block. This improves the safety and capacity level greatly, and has been deployed in several lines worldwide, such as London’ s Docklands Light Railway, New York’ s L Line, and Beijing’ s Subway Line 2. Compared with the “ fixed block” mode, in which only one train is allowed to operate in one or several block segments, a “ moving block” mode can make full use of the railway line capacity by implementing a properly designed control method.

The concept of string stability was originally proposed in Ref.  [5]. In Ref.  [6], it is redefined as the uniform boundedness of all the states with uniformly bounded initial states for a class of countably infinite interconnected nonlinear systems intuitively, which has been demonstrated to be an effective tool to study the control of an automated vehicle system and other mechanical systems.[7– 10] In the study of an automated vehicle system, the string stable is said to be true if the interval tracking errors decrease as the their propagation along the opposite moving direction, i.e., any perturbation of the speed or the location of the leading vehicle, will not give rise to amplified fluctuations to the following ones.[11] Therefore, the traffic capacity will be improved under the principle of constant spacing policy. The two major control architectures that are used in the study of multi-vehicle coordination control are predecessor following (PF) and bidirectional architecture (BA).[12– 14] In the PF mode, the controller is developed based on the relative information from its preceding vehicle, while in the BA mode, the controller is developed based on the relative information from its preceding and following vehicles. As is reported in Ref.  [15], the convergence rate of the PF mode is faster than that of the BA mode, but the PF mode suffers high algebraic growth of initial errors. At the same time, the BA mode has a better transient performance than the PF mode, and it also has a better robustness. Besides these two modes, other recent studies have reported the use of more communication structures in vehicle platoons to enhance safety. In Ref.  [16], a quantitative characterization of the impact of communication information structures and contents on vehicle platoon safety is investigated. Different information structures and contents are compared to obtain the intrinsic relationships between vehicle coordination and communications in a vehicle platoon. In Ref.  [17], leader tracking schemes for vehicle string are presented, and inter-vehicle and leader-follower spacings dynamics considering time delays are provided. In Ref.  [18], the control of vehicle platoons for highway safety and efficient utility with consideration of consensus with communications and vehicle dynamics is presented, algorithms are designed, and the corresponding convergence properties are given. Interested readers can refer to Refs.  [19]– [21] and the references therein for up-to-date theoretical and practical progress in vehicle platoons. In Ref.  [22], it is indicated that the “ string stability” of vehicle strings cannot be obtained if only relative spacing information to maintain a constant distance behind their predecessor is used in the control design. In addition, it is shown that if only relative spacing information is available for the control design, then “ string instability” is inevitable for any linear controller. From Refs.  [23] and [24], it is known that “ string instability” can be corrected via a constant time headway policy; however, a constant spacing policy is required considering the operational criteria in some special fields, [25] such as the train platoon considered in this work.

Considering the complexity, uncertainty, and inscrutability of the railway operational environment, one knows that modeling train dynamics and achieving accurate control is a considerable challenge that has aroused much effort in the control design of automatic train operation (see Refs.  [26]– [29] and the references therein). The difficulty is greatly increased when the problem rises to the modeling, control, and optimization of the train platoon. Existing research has mainly dealt with this problem on the level of scheduling and timetable optimization (see Refs.  [30] and [31] and the references therein), while little efforts has been made to model the dynamics of a train platoon and design a feedback control law, which is thus the topic of this work. In this paper, a train platoon working in the mode of a “ moving block” is considered. In the dynamics of a single train, uncertain basic and aerodynamic resistances (known as the Davis equation[27]), and unknown extra resistances and disturbance are considered simultaneously. The dynamics of single trains are connected by the objective to drive each train to the minimum separation distance (including braking distance and redundant safe distance) from the rear of the preceding train. Proximal information is used in the controller design, two control schemes are developed using prox-info of location, speed and acceleration, and using prox-info of location only. The latter requires no sensors to measure current speed and acceleration online, and a high-order sliding mode observer, named Levant’ s differentiator, [32] is used to estimate values of speed and acceleration.

The features and merits of the methods developed can be summarized briefly as follows.

(I) Local control to achieve global disposition The communication topology among trains is a bidirectional pattern, i.e., each train communicates with its neighboring ones only, which allows the control law for each train to be developed separately to some extent. This pattern alleviates the demand for global information and achieves inexpensive practical implementation. In the developed method, only real-time location information is needed in the control design and there are no requirements for real-time speed and acceleration, which eliminates the need for onboard sensors to measure them and thus alleviates the cost of period maintenance: which is a highly-desired property from the practical viewpoint.

(II) Expansibility The developed control scheme can be applied to a single train and also to a group of up-to n trains, with n > 1 being a positive constant, while there is no need to adjust the control structure and redesign the adaptation laws.

(III) Adaptivity and robustness There is no need for the precise coefficients of basic resistance, which are automatically estimated by adaptation laws. Meanwhile, the developed control schemes can compensate for any other external unmodeled resistance forces generated by tunnel, slope, curve, and disturbances.

(IV) Finite-time convergence under uncertain dynamics Although asymptotical results are not achieved, the separation errors defined to describe the relative distance can be adjusted to converge to pre-specified compact sets by running design parameters. In addition, the bound values of compact sets can be adjusted to be very small by choosing proper design parameters.

The rest of this paper is organized as follows. In Section  2, the formulated problem and some preliminaries are presented. The developed control schemes, together with stability analysis are given in Section  3. Simulation results are shown in Section  4 to verify the effectiveness of the proposed control laws. Section  5 ends this paper with some concluding remarks, and our future works are stated briefly.

2. Problem formulation and preliminaries

Consider the train platoon shown in Fig.  1, the dynamics of the train i can be described by the following equation:

where pi, ṗ i, p̈ i, and mi represent the values of position, speed, acceleration, and mass of train i, respectively; Fi is the combination of traction and braking forces; fi(vi) is the Davis equation that represents the basic operational resistance force with ai + Δ ai, bi + Δ bi, and ci + Δ ci being the coefficients, therein; ai, bi, and ci are the nominal values, while Δ ai, Δ bi, and Δ ci present the time-varying terms of these coefficients caused by complex operational environments; and, di(ṗ i, pi, t) is used to model the dynamics of other resistance generated by curve resistance, slope resistance, tunnel resistance, and other disturbance, which are in connection with current speed, position and time. Without loss of generality, the parameters mentioned above, including ai, bi, and ci are assumed to be unknown constants, while Δ ai, Δ bi, Δ ci, and di(· ) are assumed to be time-varying and bounded, i.e., , , , , with θ i being an unknown constant, . Choose ui := Fi/mi, the acceleration value of train i, as the control input to be designed and define the compounded disturbance as

in view of the above arguments and the fact that the value of speed ṗ i is always bounded from the practical engineering view, it is reasonable to assume that the compounded disturbance Di is bounded, i.e., , where is an unknown constant.

The target is to design the cooperative adaptive control law for each train to achieve the following objectives:

(i) The train i, i = 2, … , n, maintains the minimum safe separation distance Ls + Le + d1 + d2 with respect to the preceding train i − 1 to maximize the railway line capacity in the presence of uncertain operational resistance and external disturbance, for the leading train; i.e., i = 1, is used to track the pre-specified distance-to-go profile, where Ls, Le, and d1 + d2 denote braking distance, redundant safe distance, and positioning error redundant distance, respectively, where Ls is calculated from the maximum train speed to guarantee the safe operation.

(ii) Stability for each train is guaranteed in the sense that the signals in the closed-loop system for each train are kept bounded.

(iii) String stability for train platoon is guaranteed in the sense that supi | | ei(· )| | ∞ < ϑ with ϑ being a small positive constant.

To achieve these ends, the spacing error ei for i = 2, … , n marked in Fig.  1 will be shown to converge to small sets with respect to increasing time. The stability for each train and the string stability for the train platoon can be guaranteed using the Lyapunov stability theorem[33] and string stability theorem, [6] respectively.

Fig.  1. Structure of train platoon.

The string stability, introduced in Ref.  [6], of a CAAC-equipped train platoon shown in Fig.  1 is defined as follows.

Definition 1 (String stability) The origin ei = 0 shown in Fig.  1 with each train’ s dynamics modeled by Eq.  (1) is string stable, if given any ε > 0, there exists a constant δ satisfying | | ei(0)| | ∞ < δ ⇒ supi | | ei(· )| | ∞ < ε .

Lemma 1[34] Let function V(t) ≥ 0 be a continuous function defined V(t) ∈ R+ and V(0) bounded. If the following inequality holds:

where h1 > 0, h2 are constants, then it is concluded that V(t) is bounded.

3. Cooperative adaptive control design

In this section, for the train platoon under consideration, two control schemes are developed. The first is developed using prox-info of location, speed, and acceleration, while the second is developed using prox-info of location only, real-time measurements of prox-info of speed and acceleration are no longer needed by virtue of a properly designed observer.

3.1. Control design using proximal location, speed, and acceleration information

To develop a cooperative adaptive control scheme, one can define the following separation distance error for train i:

where pi and Li are the current accurate geographic location information of the front end and the length of train i, respectively. It is assumed here that pi is the location of the front of the train i. The filtered error ni = ė i + α iei will facilitate the control design and stability analysis, which is partially inspired by our previous work on adaptive control for automatic train operation, [35] where α i is a positive constant design parameter, which is briefly explained as follows. The solution of ni = ė i + α iei can be easily obtained as

It is clear that the relationship between ei and ni is governed by ei = ni/α i because t tends to infinity. Since α i is a positive constant, the convergence of ei and ni is equivalent. Furthermore, ė i decays to zero as ni from the definition of ni. The time derivative of ni can be obtained as

It is clear that equation  (4) reflects the open-loop dynamics of train i in a newly-introduced variable only, which cannot guarantee the string stability of the train platoon. To overcome this problem, the following linear weighting error can be defined to couple the information between train i and train i + 1:

where β i is a positive design parameter. It is clear that nn+ 1 does not exist, one can simply set nn+ 1 to be zero. It is necessary to point out that asymptotic convergence or ultimate boundedness of Ni for all i = 1, 2, … , n can guarantee the same property of ni. This can be easily explained by the following analysis. Let 𝒩 1 := [n1  n2  · · ·   nn]T and 𝒩 2 := [N1  N2  · · ·   Nn]T. The relationship of 𝒩 1 and 𝒩 2 is governed by 𝒩 2 = 𝓑 𝒩 1, where

since β i for i = 1, 2, … , n are design parameters, one can chose all β i > 0 such that 𝓑 is a non-singular matrix, this adequately supports the above argument.

The time derivative of Ni can be obtained as

where Fi = β ip̈ i− 1 + p̈ i+ 1 + α iβ iė i − α i+ 1ė i+ 1.

The proposed adaptive control for train i is of the form

where k1 > 0 is a constant design parameter, , ĉ i, and D̂ i are the estimations of unknown parameters bi, ci, and , respectively. The adaptation laws are designed as follows:

where ε b, ε c, ε D, σ 1, σ 2, and σ 3 are positive design parameters. σ 1, σ 2, and σ 3 are positive constants to execute σ -modification to prevent the estimation’ s drift to become very large.[36] Particularly for the train n, the proposed adaptive control is of the form

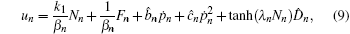
Fn = β n(p̈ n− 1 + α nė n), , ĉ n, and D̂ n are the estimations of unknown parameters bn, cn, and , respectively. The adaptation laws are

Theorem 1 (Tracking performance and boundedness of closed-loop signals) Consider a train platoon with a communication method to exchange prox-info, as shown in Fig.  1. If the adaptive control for train i is designed as Eq.  (7) (for train n is Eq.  (9) and the adaptation laws are designed as Eq.  (8) (for train n are Eq.  (10)), then all of the closed-loop system signals are ultimately uniformly bounded. Furthermore, the linear weighting error Ni and parameter estimation errors g̃ i remain within the compact sets Ω Ni and Ω gi, g ∈ {b, c, D}, respectively, as defined by

where θ i and μ 1 are defined later (see Eqs.  (17a) and (17b)).

Proof Consider Eqs.  (6), (7), and (9), the closed-loop dynamics for train i, i = 1, 2, … , n − 1, and train n can be obtained as

where is the estimation error.

Consider the following Lyapunov candidate:

the time derivative of Vi along Eqs.  (8), (10), and (12) can be obtained as

Consider the fact that

q ∈ {bi, ci, Di}, and the following inequality:[37]

it follows

with

In view of Lemma 1, it is known that Vi is ultimately bounded. Furthermore, Vi ≤ Vi(0) + θ i/μ 1 with Vi(0) being the initial value of Vi. Based on the definition of Vi, one can conclude that the linear weighting error Ni and estimation errors , c̃ i, D̃ i will be ultimately confined in the following compact sets with g ∈ {b, c, D}:

The proof is complete.

Theorem 2 (String stability of train platoon) The proposed control laws Eqs.  (7) and (9), and their corresponding adaptation laws Eqs.  (8) and (10) guarantee the string stability of a train platoon after some finite time.

Proof As to the global Lyapunov candidate Vc1, its time derivative can be obtained as

in view of Eqs.  (13a) and (19), it follows that

thus, for all i = 1, 2, … , n, the following inequality holds:

which implies that there exists a moment T such that for any t > T the following inequality is true:

that is, after some finite time T, the condition to satisfy string stability in Definition 1 is satisfied. In view of the consistency of boundedness property of Ni and ni, thus ei, the string stability of the train platoon is guaranteed.

The proof is complete.

Remark 1 It is clear that the errors Ni, , c̃ i, and D̃ i can be tuned to be small enough by setting a large-enough k1, σ 1, σ 2, σ 3, and λ i and a small-enough β i, which are all design parameters. However, increasing k1 will result in a high-gain control scheme, which may cause chattering in practical applications. It can be observed that large σ 1, σ 2, and σ 3 will amplify the θ i, which conflicts with the expectation to some extent. Actually, σ 1, σ 2, and σ 3 are small positive constants that are introduced to execute the σ -modification; [36] therefore, how to choose the optimal design parameters of k1, σ 1, σ 2, σ 3, λ i, β i simultaneously to achieve the satisfactory performance is still an open problem. In the following simulations, these parameters are tuned using a trial-and-error method.

3.2. Control design using proximal location information

It is clear that prox-info of location, speed, and acceleration and the current information of location and speed must be available and are directly used in the developed controller, as can be seen from Theorem 1. To alleviate the burden of the sensors used to measure these variables, it is desired that the developed controllers can guarantee a satisfactory performance while using less system information by virtue of the observer technique.[32, 38] In this section, cooperative adaptive controller using information of current and proximal location only is developed to achieve the same objectives. By virtue of a properly-constructed observer (which is given in detail later), it is assumed that the prox-info of speed and acceleration, and the current information of speed can be observed from the information of location with small observation errors, i.e., for all i = 1, 2, … , n, the following inequalities hold:

where is defined as the observed value of (· ), while is the observed error, with χ i1 and χ i2 being positive constants representing the observation errors. Since only location information is available for the controller design, the notations used in this section are redefined as follows:

Accordingly, the proposed cooperative adaptive control scheme is designed as follows. The proposed cooperative control for train i, i = 1, 2, … , n − 1 and the control for train n are

respectively, where k2 > 0 is the design parameter, other notations hold the same definitions as above.

Coincide with the controller Eqs.  (24a) and (24b), the adaptation laws are redesigned as

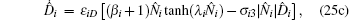
Theorem 3 (Tracking performance and boundedness of closed-loop signals) Consider a train platoon with a communication method to exchange proximal geographic information, as shown in Fig.  1. If the adaptive control for train i is designed as Eq.  (24a) (for train n is Eq.  (24b)) and the adaptation laws are designed as Eq.  (25), then all of the closed-loop system signals are ultimately uniformly bounded. Furthermore, the linear weighting error Ni remains within the compact sets Ω Ni, as defined by

where ϕ i is defined later (see Eq.  (32)).

Proof Consider a Lyapunov candidate

whose time derivative can be calculated as

Consider the property of observer in Eq.  (22) and the fact that ṗ i and p̈ i for i = 1, 2, … , n are always bounded from the practical engineering viewpoint, i.e., , with and being positive constants. Therefore, equation  (27) becomes

It is clear that V̇ b ≤ 0 if

Based on the Lyapunov theorem, [33] is ultimately bounded by

which thus definitely guarantees the boundedness of .

Similarly, we can chose a Lyapunov candidate

and calculate its derivative as

therefore, ĉ i is ultimately bounded by

which naturally guarantees the boundedness of c̃ i.

Consider a Lyapunov candidate

whose time derivative can be calculated as

in like manner, we can conclude that D̂ i is ultimately bounded by |D̂ i| ≤ (β i + 1)/σ i3.

For train n, it is easy to find that , ĉ n, and D̂ n are ultimately bounded by

respectively.

Consider the open-loop dynamics (Eq.  (6)) and controller (Eq.  24), the closed-loop dynamics for train i, i = 1, 2, … , n − 1, and train n can be obtained as

Consider the following Lyapunov candidate:

The time derivative of Vi along Eq.  (28) is obtained as

Note that

and the above arguments that , c̃ i, and D̃ i are all bounded, it follows with ϕ i being a positive constant, therefore, Ni is ultimately confined in the following compact set:

The proof is complete.

Theorem 4 (String stability of train platoon) The proposed control laws Eq.  (24) and adaptation laws Eq.  (25) guarantee the string stability of a train platoon after some finite time.

Proof The time derivative of Vc2 can be calculated as

based on a similar analysis as in the proof of Theorem 2, we can conclude that

that is, after some finite time T, the condition to satisfy the string stability in Definition 1 is satisfied.

The proof is complete.

Remark 2 It can be known clearly from this subsection that the developed control scheme can guarantee the adjustability of the tracking and estimation errors, which is similar with the previous case. How to choose the optimal design parameters to achieve the satisfactory performance is still an open problem, which is also solved via a trial-and-error method in the following simulations. What is more, the bounded values of observation errors of speed and acceleration (χ i1 and χ i2) affect the performance directly; therefore, an observer that can achieve sufficiently good observation performance is required. How to design an observer is out of the scope of this work, the observer used here is Levant’ s differentiator, [32] which is given in the following section.

4. Simulation results

To evaluate the effectiveness of the developed control schemes, we apply the results to control a 5-train platoon. The prespecified speed and location profiles for the leading train are shown in Fig.  2(a). The desired tracking spacing distance is simply set to be 150  m (which can set to be any value by actual requirement).

The initial values of speed and acceleration for all trains are all 0, the initial locations are set to be 0  m, 150  m, 300  m, 450  m, and 600  m for train i, i = 1, 2, … , 5, respectively. The parameters of train operational resistance are set as: a1 = 0.85, b1 = 0.004, c1 = 0.00016, a2 = 0.8, b2 = 0.002, c2 = 0.0002, a3 = 0.9, b3 = 0.003, c3 = 0.00018, a4 = 0.7, b4 = 0.0025, c4 = 0.0004, a5 = 0.75, b5 = 0.0035, and c5 = 0.00025. The profile of di is shown in Fig.  2(b) to simulate the external resistance.

Fig.  2. Trajectories of desired speed, location, and disturbance. (a) Prespecified speed and location profiles for train 1. (b) Profiles and di.

The design parameters are chosen as follows. For all i, α i = 4, β i = 1, ε b = ε c = ε D = 10− 7, λ i = 15, k1 = k2 = 25, σ i1 = 0.001, σ i2 = 0.01, σ i3 = 0.001, initial estimated values of , ĉ i, and D̂ i are set to be 0.8, 0.001, and 0.0001, respectively. The observer used when applying Theorem 3 is Levant’ s differentiator, [39] which is briefly described in the following lemma. One refers to Refs.  [39] and [32] for more details of Levant’ s differentiator. Here, the design parameters of the observer are γ i1 = 8, γ i2 = 6, γ i3 = 4 for all i.

Lemma 2 Consider a real-time location signal pi of train i. The following high-order sliding mode observer with γ ij, j = 1, 2, 3 being positive design parameters:

guarantees that: there exists a time moment T, such that for any t > T, one obtains p̂ i(t) = pi(t), v̂ i(t) = ṗ i(t), and â i(t) = p̈ i(t) in the absence of measurement noise in pi by choosing proper γ ij, j = 1, 2, 3. Furthermore, if a bounded Legesgue-measurable noise exists, then the estimation errors are small positive constants that depend exclusively on the parameters of Eq.  (33).

Figure  3 gives the simulation results of Theorem 1. Figure  3(a) presents the profiles of interval tracking errors. The speed and acceleration tracking performance are shown in Figs.  3(b) and 3(c), respectively. The plots of location of the five trains are given in Fig.  3(d). The results using Theorem 3 are shown in Fig.  4. Figures  4(a)– 4(d) present the interval tracking errors, speed tracking errors, acceleration tracking errors, and location versus time, respectively. The observation errors of speed and acceleration are given in Figs.  5(a) and 5(b), respectively. It is clear that satisfactory results are obtained, which confirms the effectiveness of the developed control schemes.

Fig.  3. Simulation results of Theorem 1. (a) Profiles of ei. (b) Profiles of speed tracking errors. (c) Profiles of acceleration tracking errors. (d) Trajectories of location versus time of five trains.

Fig.  4. Simulation results of Theorem 3. (a) Profiles of ei. (b) Profiles of speed tracking errors. (c) Profiles of acceleration tracking errors. (d) Trajectories of location versus time of five trains.

Fig.  5. Observation performance. (a) Speeds and their observations. (b) Accelerations and their observations.

5. Concluding remarks

In this paper, cooperative adaptive control schemes for a train platoon are developed to maintain any train at the minimum desired separation distance from the preceding train, which helps to maximize the railway traffic volume. By virtue of the modern CBTC technique, proximal information (i.e., information of preceding and following trains) is used in the controller design. After the developed control scheme using proximal information of location, speed, and acceleration, the second requires less information (only proximal information of location is required) while guaranteeing satisfactory performance with the aid of a properly constructed observer. It is proven that the developed control schemes are capable of online estimating of the unknown system parameters and ensuring the string stability of train platoon. The boundedness of all of the closed-loop signals and string stability of the train platoon are proven rigorously using the Lyapunov stability theorem. The separation distances are shown to converge to small sets that are tunable by design parameters in finite time, which is a highly desired property in practical engineering. Simulation results are presented to demonstrate the effectiveness. More actual considerations motivated by practical engineering will be incorporated in the following work, which will contain: i) information transmission delay among trains; ii) bandwidth constraint on transmission channel; iii) issues with energy efficient cooperative control; and iv) experimental validation in a real railway system.

Reference
1 Sun Y H, Cao C X, Xu Y and Wu C 2013 Chin. Phys. B 22 120501 DOI:10.1088/1674-1056/22/12/120501 [Cited within:1]
2 Wang M, Zeng J W, Qian Y S, Li W J, Yang F and Jia X X 2012 Chin. Phys. B 21 070502 DOI:10.1088/1674-1056/21/7/070502 [Cited within:1]
3 Cao C X, Xu Y and Li K P 2013 Chin. Phys. B 22 060504 DOI:10.1088/1674-1056/22/6/060504 [Cited within:1]
4 Xun J, Ning B, Li K P and Zhang W B 2013 Transp. Res. Pt. C-Emerg. Technol. 35 127 DOI:10.1016/j.trc.2013.06.008 [Cited within:1]
5 Chu K C 1974 IEEE Trans. Autom. Control 19 243 DOI:10.1109/TAC.1974.1100538 [Cited within:1]
6 Swaroop D and Hedrick J 1996 IEEE Trans. Autom. Control 41 349 DOI:10.1109/9.486636 [Cited within:3]
7 Fax J A and Murray R M 2004 IEEE Trans. Autom. Control 49 1465 DOI:10.1109/TAC.2004.834433 [Cited within:1]
8 Desai J P, Ostrowski J P and Kumar V 2001 IEEE Trans. Robot. Autom. 17 905 DOI:10.1109/70.976023 [Cited within:1]
9 Murray R M 2007 J. Dyn. Syst. Meas. Control 129 571 DOI:10.1115/1.2766721 [Cited within:1]
10 Kwon J W and Chwa D 2015 IEEE Trans. Intell. Transp. Syst. 15 2040 DOI:10.1109/TITS.2014.2308535 [Cited within:1]
11 Zhou J and Peng H 2005 IEEE Trans. Intell. Transp. Syst. 6 229 DOI:10.1109/TITS.2005.848359 [Cited within:1]
12 Ploeg J, Shukla D, Wouw N and Nijmeijer H 2014 IEEE Trans. Intell. Transp. Syst. 15 854 DOI:10.1109/TITS.2013.2291493 [Cited within:1]
13 Ghasemi A, Kazemi R and Azadi S 2015 Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 229 216 [Cited within:1]
14 Xiao L and Gao F 2011 IEEE Trans. Intell. Transp. Syst. 12 1184 DOI:10.1109/TITS.2011.2143407 [Cited within:1]
15 Hao H and Barooah P 2013 Int. J. Robust Nonlinear Control 23 2097 DOI:10.1002/rnc.2872 [Cited within:1]
16 Xu L, Wang L Y, Yin G and Zhang H 2014 IEEE Trans. Veh. Technol. 63 4206 DOI:10.1109/TVT.2014.2311384 [Cited within:1]
17 Peters A A, Middleton R H and Mason O 2014 Automatica 50 64 DOI:10.1016/j.automatica.2013.09.034 [Cited within:1]
18 Wang L Y, Syed A, Yin G G, Pand ya A and Zhang H 2014 J. Syst. Sci. Complexity 27 605 DOI:10.1007/s11424-014-2115-z [Cited within:1]
19 Alam A, Mårtensson J and Johansson K H 2015 Control Eng. Practice 38 11 DOI:10.1016/j.conengprac.2014.12.009 [Cited within:1]
20 Dafflon B, Gechter F, Gruer P and Koukam A 2015 Informatics in Control, Automation and Robotics 325 107 DOI:10.1007/978-3-319-10891-9_6 [Cited within:1]
21 Ghasemi A and Rouhi S 2015 PROMET-Traffic & Transportation 27 35 [Cited within:1]
22 Seiler P, Pant A and Hedrick K 2004 IEEE Trans. Autom. Control 49 1835 DOI:10.1109/TAC.2004.835586 [Cited within:1]
23 Eyre J, Yanakiev D and Kanellakopoulos I 1998 Vehicle System Dynamics 30 375 DOI:10.1080/00423119808969457 [Cited within:1]
24 Swaroop D 1997 California Partners for Advanced Transit and Highways (PATH) [Cited within:1]
25 Santhanakrishnan K and Rajamani R 2003 IEEE Trans. Intell. Transp. Syst. 4 198 DOI:10.1109/TITS.2003.821341 [Cited within:1]
26 Li S K, Yang L X and Li K P 2015 Chin. Phys. B 24 010503 DOI:10.1088/1674-1056/24/1/010503 [Cited within:1]
27 Dong H, Ning B, Cai B and Hou Z 2010 IEEE Circuits Syst. Mag. 10 6 DOI:10.1109/MCAS.2010.936782 [Cited within:1]
28 Yin J, Chen D and Li L 2014 IEEE Trans. Intell. Transp. Syst. 15 2561 DOI:10.1109/TITS.2014.2320757 [Cited within:1]
29 Gao S, Dong H, Chen Y, Ning B, Chen G and Yang X 2013 IEEE Trans. Intell. Transp. Syst. 14 1733 DOI:10.1109/TITS.2013.2266255 [Cited within:1]
30 Yang X, Li X, Gao Z, Wang H and Tang T 2013 IEEE Trans. Intell. Transp. Syst. 14 438 DOI:10.1109/TITS.2012.2219620 [Cited within:1]
31 Su S, Tang T, Li X and Gao Z 2014 IEEE Trans. Intell. Transp. Syst. 15 673 DOI:10.1109/TITS.2013.2285737 [Cited within:1]
32 Levant A 2003 Int. J. Control 76 924 DOI:10.1080/0020717031000099029 [Cited within:4]
33 Khalil H K and Grizzle J 2002 Nonlinear Systems Prentice hall Upper Saddle River [Cited within:2]
34 Ge S S and Wang C 2004 IEEE Trans. Neural Netw. 15 674 DOI:10.1109/TNN.2004.826130 [Cited within:1]
35 Gao S, Dong H, Chen Y, Ning B and Chen G 2013 Control Intell. Syst. 41 103 DOI:10.2316/Journal.201.2013.2.201-2451 [Cited within:1]
36 Ioannou P A and Kokotovic P V 1984 Automatica 20 583 DOI:10.1016/0005-1098(84)90009-8 [Cited within:2]
37 Polycarpou M M 1996 IEEE Trans. Autom. Control 41 447 DOI:10.1109/9.486648 [Cited within:1]
38 Lee K W and Khalil H K 1997 Int. J. Control 67 869 DOI:10.1080/002071797223839 [Cited within:1]
39 Levant A 1998 Automatica 34 379 DOI:10.1016/S0005-1098(97)00209-4 [Cited within:2]