†Corresponding author. E-mail: shengganglinew@126.com
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11401243 and 61403157), the Fundamental Research Funds for the Central Universities of China (Grant No. GK201504002), and the Natural Science Foundation for the Higher Education Institutions of Anhui Province of China (Grant No. KJ2015A256).
In this paper the synchronization for two different fractional-order chaotic systems, capable of guaranteeing synchronization error with prescribed performance, is investigated by means of the fractional-order control method. By prescribed performance synchronization we mean that the synchronization error converges to zero asymptotically, with convergence rate being no less than a certain prescribed function. A fractional-order synchronization controller and an adaptive fractional-order synchronization controller, which can guarantee the prescribed performance of the synchronization error, are proposed for fractional-order chaotic systems with and without disturbances, respectively. Finally, our simulation studies verify and clarify the proposed method.
In the last two decades, the study of fractional calculus has become an attractive research field from both theoretical and application perspectives because it naturally relates to systems with memory, which prevail in most physical systems.[1– 9] Recently, synchronization for fractional-order chaotic systems has received increasing attention due to its potential applications in control processing and secure communication. For example, global non-fragile synchronization of a class of new fractional-order chaotic system is studied in Ref. [10]. A new method of fast projective synchronization for fractional-order dynamical systems is introduced in Ref. [11]. Synchronization between two fractional-order chaotic systems, which exhibits interesting behavior such as two, three, and four scrolls, is presented in Ref. [12]. Some more studies attempting to synchronize fractional-order chaotic systems can be found in Refs. [13]– [22], etc.
Another important issue associated with the synchronization of chaotic systems is the synchronization error satisfying a prescribed performance. By prescribed performance we mean that the synchronization error should converge to the origin, with a convergence rate that is no less than a priori given performance function. Prescribed performance controllers have been first proposed in Refs. [23] and [24] for affinity in the control integer-order nonlinear system structures. These results have been extended in Ref. [25] to investigate the tracking problem with guaranteed prescribed performance and contact maintenance in the presence of structural uncertainties and parameters. In Ref. [26], an approximation-free state feedback control method is given for unknown pure feedback systems, which is capable of guaranteeing, for any initial system condition, output tracking with prescribed performance and bounded closed loop signals. Up to now, the positive results of prescribed performance control of integer-order nonlinear systems has been fruitful (see, Refs. [27]– [36], etc). Compared with integer-order calculus, fractional-order calculus offers a more powerful tool for describing hereditary and memory properties of the systems. Fractional-order operator is nonlocal in the sense that it considers the fact that the future system states depends not only on the present states but also on all history of its previous states. For fractional-order systems, it is very difficult to analyze the stability by finding its dominant roots or by using other algebraic methods, which are commonly used in the stability of integer-order systems. To date, the direct check of the stabilities of fractional-order nonlinear systems by using polynomial criteria are still not possible, because the characteristic equation of the fractional-order system is not a polynomial but a pseudo-polynomial function of fractional powers of the complex variable s.[37] In a manner of speaking, most of the existing control schemes for integer-order systems cannot be extended to fractional-order systems directly. To our best knowledge, the prescribed performance control for fractional-order nonlinear systems has not been reported in the relevant literature. Thus it is meaningful to design a kind of effective prescribed performance control method for fractional-order nonlinear systems.
Motivated by the aforementioned observations, in this paper, we focus on the prescribed performance synchronization between two different fractional-order chaotic systems with and without an unknown external disturbance. There are three main contributions which are worth emphasizing as follows. (I) It is the first work that investigates the prescribed performance control of fractional-order nonlinear systems. (II) An adaptive fractional-order controller is designed for synchronizing two different fractional-order chaotic systems with external disturbances. It should be pointed out that the fractional integration of sign function is used in the controller design, so the chattering phenomenon will not occur in this paper. (III) A reasonable assumption is proposed, which may provide some assistance to cope with external disturbance in fractional-order systems.
In this subsection, some basic preliminaries for fractional differential and integral equations are given (please refer to Ref. [1] for more details). The lower limit of the fractional calculus is set to be 0 in this paper. The fractional-order integral with order α can be expressed as
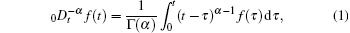
where Γ (· ) represents the Euler Gamma function.
There are three definitions of fractional-order derivative which are often used in the literature, that is: Grunwald– Letnikov (G– L), Riemann– Liouville, and Caputo definitions. The Caputo derivative is frequently used in control engineering because the initial conditions of Caputo derivative take on the same form as those in integer-order systems. The Caputo fractional derivative with order α is given as
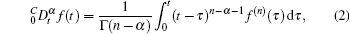
where n − 1 ≤ α < n. For convenience, in the rest of this paper we always assume that α ∈ (0, 1).
The following results will be used in this paper.
Lemma 1[38] If x(t) ∈ C1[0, T] for some T > 0, then
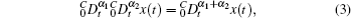
where α 1, α 2 > 0 and α 1 + α 2 ≤ 1.
Lemma 2[1] If x(t) ∈ C1[0, T] for some T > 0, and 0 < α ≤ 1, then the following equations hold:
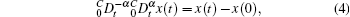
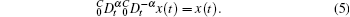
Let the fractional-order drive system and response system respectively be

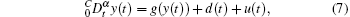
where x(t) = [x1(t), … , xn(t)]T ∈ 𝓡 n and y(t) = [y1(t), … , yn(t)]T ∈ 𝓡 n are the system state vectors which are assumed to have continuous derivatives, f(x(t)) = [f1(x(t)), … , fn(x(t))]T ∈ 𝓡 n and g(y(t)) = [g1(y(t)), … , gn(y(t))]T ∈ 𝓡 n are two continuous nonlinear functions, u(t) = [u1(t), … , un(t)]T ∈ 𝓡 n represents the control input, and d(t) = [d1(t), … , dn(t)]T ∈ 𝓡 n corresponds to unknown external disturbance. The objective of this paper is to construct a proper controller so that the following two properties are guaranteed:
Property 1 The synchronization error e(t) = x(t) − y(t) = [e1(t), … , en(t)]T converges to origin asymptotically, and all of the signals in the closed-loop system remain bounded.
Property 2 The prescribed transient and steady state behavioral bounds on the tracking error ei(t) are achieved.
Property 2 can be guaranteed with the help of the performance function which converts the prescribed performance characteristics into tracking error constraints.
Definition 1[23, 24] A smooth function φ : R+ → R+ − {0} is called performance function if φ (t) is strictly decreasing and satisfies 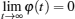
As a result, we can guarantee Property 2 by satisfying
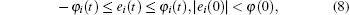
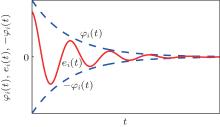
for all t ≥ 0, i = 1, 2, … , n and φ i(t) is a performance function associated with the synchronization error e(t). The decreasing rate of the performance function φ i(t) gives a lower bound on the required speed of convergence of synchronization error ei(t). The aforementioned properties can be seen in Fig. 1.
Remark 1 It should be mentioned that if inequality equation (8) is satisfied, then the synchronization error will converge to zero asymptotically, with a convergence rate no less than a certain pre-specified value, exhibiting that the maximum overshoot is less than some sufficiently small preassigned constant. Prescribed performance synchronization can be well used in many fields, such as precise synchronization, finite-time synchronization, etc. In fact, if the prescribed performance function is chosen appropriately, then the finite-time synchronization (for example, see Refs. [39]– [41]) turns into only a special case of the prescribed performance synchronization.
Remark 2 Traditional synchronization controller design for fractional-order systems, guarantees the convergence of the synchronization error to a residual set, whose size depends on control system design parameters and some bounded terms (see, Refs. [13]– [22], etc). However, no systematic procedure exists to precisely estimate the required upper bounds, thus making an a priori choice of the aforementioned design parameters to satisfy some steady-state behaviors. Moreover, the performance of transient behaviors (i.e., overshoot and convergence rate) is difficult to analyze, even in the case of known nonlinearities. In this paper, the introduced performance function and the following synchronization error transformation will help us to solve this problem.
To meet the synchronization objective, we define an error transformation which can transform the original nonlinear system into an equivalent unconstrained system. We define
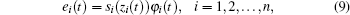
where φ i(t) is the performance function, and zi(t) is the transformed synchronization error. The introduced function si(· ) is smooth and strictly increasing, and satisfies the following conditions:

Remark 3 From the definition of the function si(· ), we know that it is an invertible function. In fact, there are many common functions satisfying the definition of si(· ). For example, tanh(zi), 2arctan(zi)/π , etc.
From the above discussion, we know that if zi(t) can keep bounded, then we have − 1 < si(zi(t)) < 1, thus – φ i(t) < ei(t) < φ i(t). Noting that φ i(t) converges to 0 asymptotically, to achieve Properties 1 and 2, we only need to design a proper controller such that zi(t) keeps bounded. According to Remark 3 we know that the inverse transformation of zi(t)

is well defined. Differentiating Eq. (11) with respect to time gives

Let
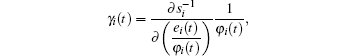
then equation (12) can be arranged as
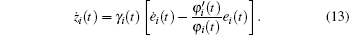
From Lemma 1 we know
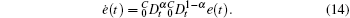
By substituting Eqs. (6), (7), and (14) into Eq. (13), we have
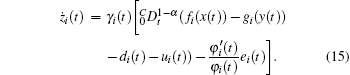
Now we consider synchronization of systems (6) and (7) without unknown external disturbances (i.e., d(t) ≡ 0). Then, we can design the following fractional synchronization controller:
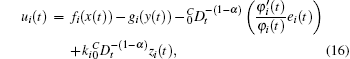
where ki is a positive design parameter.
From the above discussion, we have the following results.
Theorem 1 Consider the fractional-order drive system (6) and response system (7) on the assumption that d(t) ≡ 0. Then the proposed fractional-order controller, defined by Eq. (16), guarantees the following properties: (i) All of the signals in the closed-loop system are bounded. (ii) The prescribed performance synchronization between two fractional-order chaotic systems is achieved.
Proof According to Lemma 2 we have
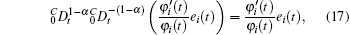
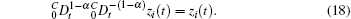
Substituting Eqs. (16)– (18) into Eq. (15) yields
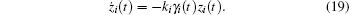
Define the Lyapunov function candidate as 
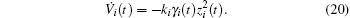
As a result, zi(t) is bounded for all t > 0. Because system (6) represents a chaotic system, we have both xi(t) and fi(x(t)) that are bounded. Furthermore, we have | ei(t)| ≤ φ i(t), which means that the synchronization error converges to origin asymptotically and the system variables xi(t) and yi(t) are bounded. From the above discussion, we have that Properties 1 and 2 can be guaranteed. This completes the proof of Theorem 1.
Most practical systems suffer from several kinds of system uncertainties (such as the modeling errors, the plant parameter variations, and the unknown external disturbances) which can actually degrade the control performance if not well-disposed.[42– 44] In this subsection, we consider the case where external disturbance d(t) cannot be neglected in chaos synchronization.
To proceed, the following assumption is needed.
Assumption 1 There exists some unknown positive constant ci such that
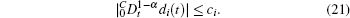
Remark 4 Assumption 1 is not very restrictive, because the upper bound of fractional derivative of the external disturbance is assumed to be unknown. There are some frequently used external disturbance functions satisfying Assumption 1, such as sin(· ), cos(· ), etc. In fact, we denote
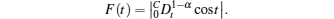
Let 

Similarly, we can obtain that G(3π ) ≥ 0 and G(4π ) ≤ 0. By using mathematical induction, we can easily conclude that G((2n – 1)π ) ≥ 0 and G(2nπ ) ≤ 0, 
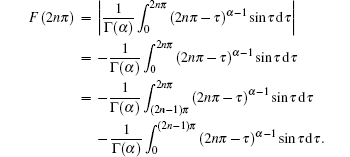
Noting that
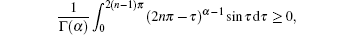
(by using the above method), we have
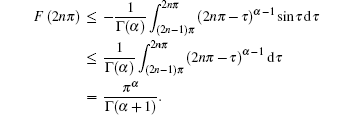
For all t > 0, there exists some 
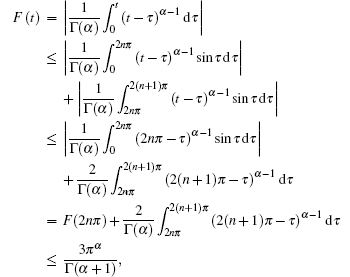
which means that 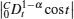
Remark 5 It should be pointed out that Assumption 1 is first proposed in this paper, and it may be helpful for tackling some periodic external disturbances in fractional-order systems.
We construct the following synchronization controller:
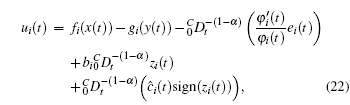
where bi is a positive design parameter, and ĉ i(t) represents the estimation of the unknown constant ci. We denote the estimation error of ci as
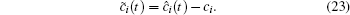
From the above discussion, we are now ready to give the following results.
Theorem 2 Consider the prescribed performance synchronization between two fractional-order chaotic systems (6) and (7). Supposing that Assumption 1 is satisfied, then the proposed adaptive fractional-order controller (22) with the adaptation law:
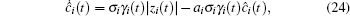
where ai and σ i are positive design parameters, can guarantee that all signals in the closed-loop system will remain bounded and the prescribed performance synchronization between systems (6) and (7) can be obtained.
Proof Substituting the controller (22) into Eq. (15) yields

By multiplying both sides of Eq. (25) with zi(t), and using Assumption 1, we have

Define the Lyapunov function candidate as
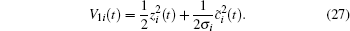
The derivative of V1i(t) with respect to time is

Using Eqs. (24) and (26), we have
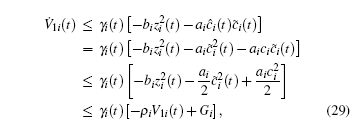
where 
Following the same manipulators as those in Ref. [45] (see, p. 14748, Eqs. (48)– (50)), we know there exists some positive constant t0i such that
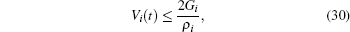
for all t > t0i. As a result, we know that both zi(t) and c̃ i(t) will keep bounded.
Thus, after the same discussion as that in the proof of Theorem 1, we know the prescribed performance synchronization between systems (6) and (7) is achieved, and the proof of Theorem 2 is ended.
Remark 6 The two terms in Eq. (24) have different applications. The σ iγ i(t)| zi(t)| is used to cancel a term which is produced by differentiating a quadratic Lyapunov function, and the other is introduced for the parameter boundedness purpose.
Simulation results are presented in this section to show the effectiveness of the proposed hybrid control scheme.
The drive system is supposed to be the generalized fractional-order Lotka– Volterra system, which can be expressed as
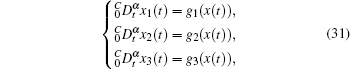
where 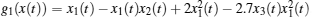

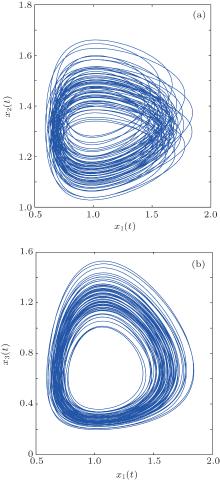 | Fig. 2. Chaotic behaviors of the generalized fractional-order Lotka– Volterra system with α = 0.96 in (a) x1(t)– x2(t) plane and (b) x1(t)– x3(t) plane. |
The response system is chosen as a complicated fractional-order three-dimensional (3D) saturated multi-scroll chaotic system. This system can be described by
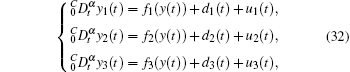
with
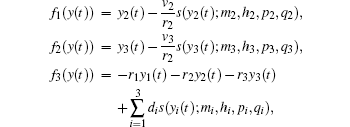
where the saturated function series s(y; g, h, p, q) is defined as

When y(0) = [1.8, 0.5, 0.3]T, r1 = v1 = 0.7, r2 = r3 = v2 = v3 = 0.8, m1 = 100, h1 = 200, m2 = m3 = 40, h2 = h3 = 80, pi = qi = 2, the fractional-order α = 0.96, and di(t) = ui(t) = 0, system (32) has a 3D 6 × 6 × 6-grid scroll chaotic attractor, which is shown in Fig. 3.
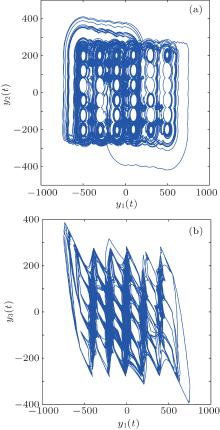 | Fig. 3. Chaotic behaviors of the 3D saturated multi-scroll fractional-order chaotic system with α = 0.96 in (a) y1(t)– y2(t) plane and (b) y1(t)– y3(t) plane. |
Throughout the simulation, the initial conditions are x(0) = [1, 1.4, 1]T and y(0) = [1.8, 0.5, 0.3]T, i.e., e(0) = [− 0.8, 0.9, 0.7]T. The performance functions are chosen as φ 1(t) = φ 2(t) = φ 3(t) = e− 0.3t. The parameters of the two fractional-order chaotic systems are chosen to be the same as the above. The three functions, s1(z1), s2(z2), and s3(z3) are supposed to be
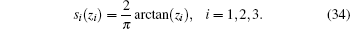
It is clear that s1(z1), s2(z2), and s3(z3) are all smooth, strictly increasing functions and satisfy condition (10).
Let di(t) = 0, i = 1, 2, 3. The controller design parameters are chosen as k1 = k2 = k3 = 1. The simulation results are shown in Figs. 4 and 5. The evolution of the synchronization errors e1(t), e2(t), and e3(t) are illustrated in Fig. 4. along with their corresponding performance bounds. The required control inputs ui(t), i = 1, 2, 3 and the transformed synchronization errors zi(t), i = 1, 2, 3 are depicted in Fig. 5. Obviously, synchronization with prescribed performance, by using the reasonable control inputs, is achieved as predicted by the theoretical analysis.
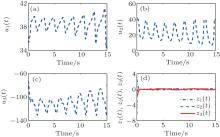
Let the external disturbances be d1(t) = 0.4sin(t), d2(t) = 0.4cos(t), and d3(t) = − 0.4sin(t). The design parameters are chosen as σ i = 5, ai = 0.2, bi = 1, and i = 1, 2, 3. Simulation results are given in Figs. 6– 8, from which we can see that the prescribed performance synchronization between systems (32) and (31) is achieved, despite the unknown external disturbances. It should be pointed out that chattering phenomenon will not occur in this paper due to the fact that the fractional-order integration of the non-continuous term sign(· ) in the control input (22) is continuous.
 | Fig. 6. Simulation results with external disturbances. The inset is the enlarged figure in the range of 11 s– 15 s. |
In this paper, a framework is constructed to achieve the prescribed performance synchronization between two different fractional-order chaotic systems. A fractional-order controller and an adaptive fractional-order controller are designed for systems without and with external disturbances, respectively. A reasonable assumption with respect to the external disturbances in fractional-order systems is proposed. Our further investigations will include working towards relaxing the requirements for the knowledge of external disturbances, designing the prescribed performance controllers for fractional-order systems with system uncertainties, while maintaining the simplicity of the controller design.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|