Cite this Article
Wei Qing-Lai, Song Rui-Zhuo†, Sun Qiu-Ye, Xiao Wen-Dong. Off-policy integral reinforcement learning optimal tracking control for continuous-time chaotic systems. Chinese Physics B, 24(9): 090504  
Permissions
Off-policy integral reinforcement learning optimal tracking control for continuous-time chaotic systems
Wei Qing-Laia), Song Rui-Zhuo†b), Sun Qiu-Yec), Xiao Wen-Dongb)
The State Key Laboratory of Management and Control for Complex Systems, Institute of Automation, Chinese Academy of Sciences, Beijing 100190, China
School of Automation and Electrical Engineering, University of Science and Technology, Beijing 100083, China
School of Information Science and Engineering, Northeastern University, Shenyang 110004, China

†Corresponding author. E-mail: ruizhuosong@ustb.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant Nos. 61304079 and 61374105), the Beijing Natural Science Foundation, China (Grant Nos. 4132078 and 4143065), the China Postdoctoral Science Foundation (Grant No. 2013M530527), the Fundamental Research Funds for the Central Universities, China (Grant No. FRF-TP-14-119A2), and the Open Research Project from State Key Laboratory of Management and Control for Complex Systems, China (Grant No. 20150104).

Abstract

This paper estimates an off-policy integral reinforcement learning (IRL) algorithm to obtain the optimal tracking control of unknown chaotic systems. Off-policy IRL can learn the solution of the HJB equation from the system data generated by an arbitrary control. Moreover, off-policy IRL can be regarded as a direct learning method, which avoids the identification of system dynamics. In this paper, the performance index function is first given based on the system tracking error and control error. For solving the Hamilton–Jacobi–Bellman (HJB) equation, an off-policy IRL algorithm is proposed. It is proven that the iterative control makes the tracking error system asymptotically stable, and the iterative performance index function is convergent. Simulation study demonstrates the effectiveness of the developed tracking control method.

PACS: 05.45.Gg
Keyword: adaptive dynamic programming; approximate dynamic programming; chaotic system; optimal tracking control
1. Introduction

The research on the control problems of chaotic systems has a dramatic increase over decades.[1, 2] Lots of control methods have been developed, such as the impulsive control method, [3– 5] the adaptive dynamic programming method, [6, 7] and neural adaptive control method.[8] In addition, the optimal tracking control problem is often encountered in the industrial process, and so it has recently been the research focus of many researchers.[9– 11]

In recent years, the adaptive dynamic programming (ADP) method has attracted a great deal of attention in the control field, which is one of the most useful intelligent control methods for solving nonlinear Hamilton– Jacobi– Bellman (HJB) equations.[12– 17] In Ref. [18], a novel numerically adaptive learning control scheme based on ADP was developed to solve optimal control problems numerically, which is the first result of applying numerical ADP to solve optimal control problems of nonlinear systems. In Ref. [19], the optimal tracking control scheme was presented based on policy iterative for discrete-time chaotic systems. However, due to the large scale and complex manufacturing techniques, many industrial dynamics are difficult to estimate and cannot be accurately obtained.[20– 22] Therefore, optimal adaptive controllers have been designed using indirect techniques, whereby the unknown plant is first identified and then the HJB equation is solved.[23, 24]

Integral reinforcement learning (IRL) is conceptually based on the policy iteration (PI) technique, and it allows the development of a Bellman equation that does not contain the system dynamics. It is worth noting that most of the IRL algorithms are on-policy, i.e., the performance index function is evaluated by using system data generated with policies being evaluated. In this paper, an off-policy IRL algorithm is estimated to obtain the optimal tracking control of the unknown chaotic systems. To obtain the steady control, the internal dynamics is obtained by an approximate structure; however, for preventing the accumulation of approximation error of internal dynamics, the off-policy IRL method is developed to obtain the optimal tracking control. It is proven that the iterative control makes the system asymptotically stable, and the iterative performance index function is convergent.

The rest of the paper is organized as follows. In Section 2, the problem motivations and preliminaries are presented. In Section 3, the off-policy IRL optimal tracking control methods are considered. In Section 4, two examples are given to demonstrate the effectiveness of the proposed optimal tracking control scheme. In Section 5, the conclusion is drawn.

2. System description and problem statement

In this paper, we consider a kind of continuous-time systems whose trajectories are contained in a chaotic attractor. The formulation is given as follows:

where x ∈ Rn is the system state and u(x) ∈ Rm is the system control, denoting u(x(t)) = u(t), f(x) and g(x) are smooth functions, f(x) represents the internal system dynamics, which is an unknown function. Actually, many nonlinear chaotic dynamical systems can be expressed as in Eq. (1), such as the Lü system, [25] Chen system, [26] Rö ssler system, Lorenz system, [27] several variants of Chua’ s circuits, [28] and the Duffing oscillator.[29]

Let θ ∈ Rn be the desired vector and ue be the steady control, define the tracking error as z = x − θ and the tracking control error as v = u − ue. The design objective of this paper is to find an optimal tracking control law, which not only drives the system (1) to track the desired objective θ , but also minimizes the following performance index function:

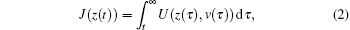
where U(z(t), v(t)) = zT(t)Qz(t) + vT(t)Rv(t) is the utility function, and Q and R are symmetric positive definite matrices.

From Eq. (2), we can have the following IRL expression:

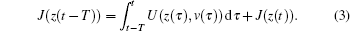
Remark 1 In this paper, ue is the steady control, which is obtained from ue = g− 1f. Here, we notice that the internal dynamics f is an unknown function, so the following approximate structure can be used to get f:

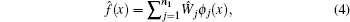
where ϕ j is a linearly-independent smooth basis function with ϕ j(0) = 0, Ŵ j is the weight and can be solved in the sense of least squares. For the internal dynamics of the chaotic system, if the input data are given, then the output data can be collected. Thus, the input-output data is used to approximate f(x).

For solving the optimal tracking control problem, we define the Hamiltonian

Thus, the optimal performance index function satisfies the HJB equation

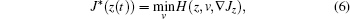
then the optimal tracking control is

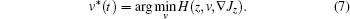
Note that the tracking error can be given as

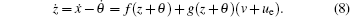
Denote F(z) = f(z + θ ) + g(z + θ )ue and G(z) = g(z + θ ), then tracking error system (8) can be expressed as

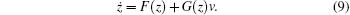
The optimal tracking control for the tracking error system is obtained by differentiating (6) with respect to v, then we have

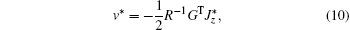
where .

The aim of this paper is to obtain the optimal tracking control v* . Thus, an off-policy ADP algorithm will be proposed in the next section to obtain J* and v* .

3. Off-policy IRL based ADP algorithm

In this section, the policy iteration algorithm is first introduced. Then, the off-policy IRL based ADP algorithm is developed to obtain J* and v* . The convergence of the off-policy IRL based ADP algorithm is proven. Finally, the weights update methods for the critic and action networks are given.

We mention that if the associated performance index function J(z) is C1, then the Bellman equation is an infinitesimal equivalent to Eq. (2) as follows:

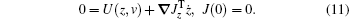
To solve Eq. (11), the following policy iterative algorithm is given in Algorithm 1 to obtain J[i] and v[i].

Algorithm 1 IRL based ADP algorithm

Initialization

Given an admissible control v[0].

Update

Solve J[i] by

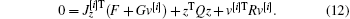
Tracking control can be updated by

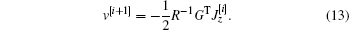
In the following subsection, the theorems will be given to prove that the developed IRL based ADP algorithm is convergent.

3.1. Convergence analysis of IRL based ADP algorithm

In this subsection, we will give two theorems. The first one is the stability of the closed-loop system with input control v[i]. The second one is about the convergence of the iterative performance index function.

Theorem 1 Define the iterative performance index function J[i] satisfying Eq. (12), the iterative tracking control input v[i+ 1] as in Eq. (13), then the closed-loop system is asymptotically stable.

Proof Taking the derivative of J[i] along the system F + Gv[i+ 1], we can have

From Eq. (12), we can obtain

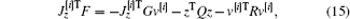
then we have

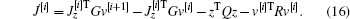
According to Eq. (13), it can be obtained

then equation (16) can be expressed as

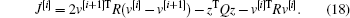
As R is symmetric positivedefinite, then we can let Λ be a diagonal matrix with its values being the singular values of R and H be an orthogonal symmetric matrix. Therefore, R = HΛ H. Let y[i] = Hv[i], then v[i] = H− 1y[i]. Thus, equation (18) can be written as

As the singular values Λ kk > 0, then we have

Therefore, we can say that the iterative control input makes the tracking error system asymptotically stable.

From Theorem 1, it can be seen that each iteration control input stabilizes the tracking error system asymptotically. The next theorem indicates that the iterative performance index function is a convergent sequence.

Theorem 2 Let J[i] be the unique positive-definite function satisfying Eq. (12), and v[i+ 1] is defined as Eq. (13), then J* (z) ≤ J[i+ 1] ≤ J[i].

Proof According to Eq. (12), we obtain

From Eq. (21), we have

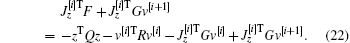
From Eqs. (17), equation (22) can be expressed as

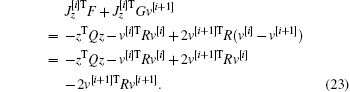
On the other side, if we take the derivatives of J[i+ 1] and J[i] along the system F+ Gv[i+ 1], respectively. Then we have

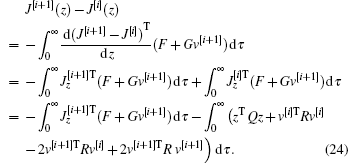
According to Eq. (21), we can obtain

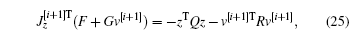
then equation (24) is expressed as

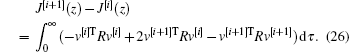
From the proof of Theorem 1, equation (26) can be written as

Moreover, it can be shown by contradiction that J* ≤ J[i + 1]. Therefore, it can be concluded J* ≤ J[i+ 1] ≤ J[i].

3.2. Off-policy IRL method

It is mentioned that in the policy algorithm, the unknown function f is necessary. Thus, for preventing the accumulation of approximation error f̃ = f̂ − f. In the following part, the off-policy algorithm is presented to calculate Eqs. (12) and (13) without f.

For v[i] given in Eq. (13), the tracking error system (9) is expressed as

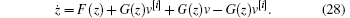
According to Eq. (12), we have the following off-policy Bellman equation:

where w[i] = G(z)v − G(z)v[i]. In the following part, we will present critic and action networks, which are used to approximate J[i] and v[i].

The critic network is given as follows:

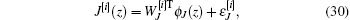
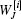
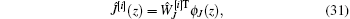
where is the ideal weight of the critic network, ϕ J (z) is the active function, and is the residual error. The estimation of J[i](z) is given as follows:

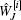
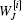
where is the estimation of .

The action network is given as follows:

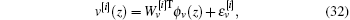
where 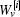is the ideal weight of the action network, ϕ v(z) is the active function, and is the residual error. Accordingly, the estimation of v[i](z) is given as follows:

Therefore, we have

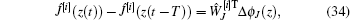
where Δ ϕ J (z) = Δ ϕ J (z(t)) = ϕ J (z(t)) − ϕ J (z(t − T)). According to the properties of Kronecker Products, we have

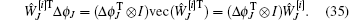
According to Eq. (13), we have

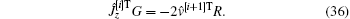
Thus, we can obtain

According to Eqs. (34)– (37), we can define the Bellman error as follows:

Let

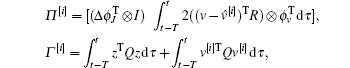
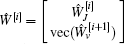
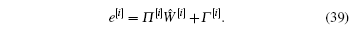
and , then the following equation can be obtained:

From Eq. (39), we can see that if the Bellman error e[i] is close to zero, then the weights of critic and action networks are obtained. Therefore, in the following subsection, two methods are used to solve Eq. (39).

3.3. Methods for updating weights

The first method is the direct method.[30] If Π [i] has a full column rank, then Γ [i] can be directly solved as follows:

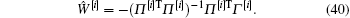
The second method is the indirect method. Let E[i] = 1/2e[i]Te[i], then according to the gradient descent method, we have

where γ > 0.

Therefore, the realization process of the presented method is summarized as follows.

Algorithm 2 Direct/indirect method

Initialization

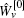
, , ε , and the initial admissible control v.

Update

Step 1a (Direct method): Compute Ŵ [i] from Ŵ [i] = − (Π [i]TΠ [i])− 1Π [i]TΓ [i].

Step 1b (Indirect method): Update Ŵ [i] by Eq. (43).

Step 2 Compute Ĵ [i] and v̂ [i].

Step 3 If | Ĵ [i+ 1] − Ĵ [i]| ≤ ε , then the corresponding v[i] is the control input, stop.

Step 4 Else, goto Step 1.

Remark 2 In this paper, we have given two methods to update the weights of the neural networks, including direct and indirect methods. For the direct method, it is necessary to collect large enough data that have full column rank to reduce the training error. For the indirect method, the gradient descent method is used to train the neural networks. It is necessary to implement more iterations to reduce the approximation error.

4. Simulation study
4.1. Example 1

In 1963, Lorenz proposed a simple model which describes the unpredictable behavior of the weather. The dynamic of the Lorenz system can be written as

where

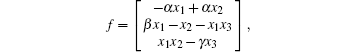
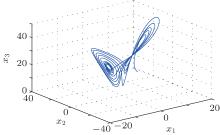
and g = diag(10, 10, 10). Let α and β be relative to the Prandtl number and Rayleigh number, respectively, γ belongs to a geometric factor. Let α = 10, β = 28, and γ = 8/3. The internal dynamics of the Lorenz system act as a two-lobed pattern called the butterfly effect, as shown in Fig. 1.

Fig. 1. Lorenz chaotic attractor.

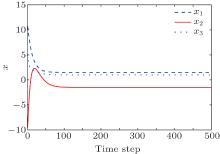
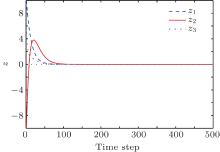
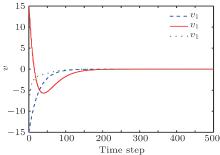
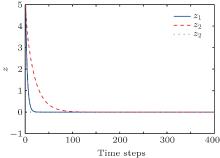
Let the desired objective be θ = [1.5; − 1.5; 1]. The initial weights of critic and action networks are selected in (− 1, 1). By one of the methods presented in Subsection 3.3, we can get the weights convergence to WJ = [0.017; − 0.06; 0.04], and Wv = [0.070, − 0.048, − 0.019; 0.0117, 0.085, − 0.063; 0.080, − 0.006, 0.071; − 0.016, − 0.049, 0.0169; − 0.028, − 0.014, − 0.024; − 0.002, 0.040, − 0.055]. After 500 time steps, the system state trajectories are given in Fig. 2, and the tracking error trajectories are shown in Fig. 3. The control error trajectories are given in Fig. 4. It can be seen that the proposed method can make the chaotic system track the desired objective.

Fig. 2. System state trajectories.

Fig. 3. Tracking error system state.

Fig. 4. Tracking control error.

4.2. Example 2

We consider the Lü system, [25, 31, 32] which is described by

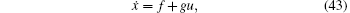
where

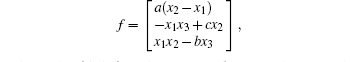
and g = diag(5, 5, 5). When a = 36, b = 3, and c = 20, the internal system Eq. (43) is shown in Fig. 5.

Fig. 5. Lü chaotic attractor.

Let the desired trajectories be θ = [2; − 2; 0.5]. The initial weights of critic and action networks are selected in (− 0.5, 0.5). Based on the proposed method, the weights of critic and action networks converge to WJ = [0.0093; − 0.0454; 0.0489] and Wv = [− 0.0196, − 0.0165, − 0.0324; − 0.0848, − 0.0899, 0.0799; − 0.0520, 0.0804, − 0.0260; − 0.0753, 0.0889, − 0.0777; − 0.0632, − 0.0018, 0.0560; − 0.0520, − 0.0021, − 0.0220]. After 400 time steps, the chaotic system trajectories are shown in Fig. 6. The tracking error trajectories and control error trajectories are given in Figs. 7 and 8. From the simulation results, it is clear that the developed optimal tracking method is effective.

Fig. 6. Lü chaotic attractor.

Fig. 7. Lü chaotic attractor.

Fig. 8. Lü chaotic attractor.

5. Conclusion

This paper proposes a new ADP method to solve the optimal tracking control of continuous-time chaotic systems. The performance index function is composed by the state tracking error and the tracking control error. The IRL is presented to obtain the iterative performance index function and control. As the chaotic system is unknown, the off-policy is proposed to overcome the unknown dynamics. It is proven that the iterative control makes the system asymptotically stable, and the iterative performance index function is convergent. Simulation study demonstrates the effectiveness of the proposed optimal tracking control method.

Reference
1 Lü J and Lu J 2003 Chaos Soliton. Fract. 17 127 DOI:10.1016/S0960-0779(02)00456-3 [Cited within:1]
2 Xu C and Wu Y 2015 Appl. Math. Model. 39 2295 [Cited within:1]
3 Ma T, Zhang H and Fu J 2008 Chin. Phys. B 17 4407 DOI:10.1088/1674-1056/17/12/013 [Cited within:1]
4 Ma T and Fu J 2011 Chin. Phys. B 20 050511 DOI:10.1088/1674-1056/20/5/050511 [Cited within:1]
5 Yang D 2014 Chin. Phys. B 23 010504 DOI:10.1088/1674-1056/23/1/010504 [Cited within:1]
6 Song R, Xiao W, Sun C and Wei Q 2013 Chin. Phys. B 22 090502 DOI:10.1088/1674-1056/22/9/090502 [Cited within:1]
7 Song R, Xiao W and Wei Q 2014 Chin. Phys. B 23 050504 DOI:10.1088/1674-1056/23/5/050504 [Cited within:1]
8 Gao S, Dong H, Sun X and Ning B 2015 Chin. Phys. B 24 010501 DOI:10.1088/1674-1056/24/1/010501 [Cited within:1]
9 Wei Q and Liu D 2014 IEEE Trans. Autom. Sci. Eng. 11 1020 DOI:10.1109/TASE.2013.2284545 [Cited within:1]
10 Wei Q and Liu D 2015 Neurocomputing 149 106 DOI:10.1016/j.neucom.2013.09.069 [Cited within:1]
11 Zhang H, Song R, Wei Q and Zhang T 2011 IEEE Trans. Neural Netw. 22 1851 DOI:10.1109/TNN.2011.2172628 [Cited within:1]
12 Heydari A and Balakrishnan S 2013 IEEE Trans. Neural Netw. Learn. Syst. 24 145 DOI:10.1109/TNNLS.2012.2227339 [Cited within:1]
13 Song R, Zhang H, Luo Y and Wei Q 2010 Neurocomputing 73 3020 DOI:10.1016/j.neucom.2010.07.005 [Cited within:1]
14 Xu X, Hou Z, Lian C and He H 2013 IEEE Trans. Neural Netw. Learn. Syst. 24 762 DOI:10.1109/TNNLS.2012.2236354 [Cited within:1]
15 Zhang H, Wei Q and Liu D 2011 Automatica 47 207 DOI:10.1016/j.automatica.2010.10.033 [Cited within:1]
16 Luo B, Wu H, Huang T and Liu D 2014 Automatica 50 3281 DOI:10.1016/j.automatica.2014.10.056 [Cited within:1]
17 Luo B, Wu H and Huang T 2015 IEEE Trans. Cybernetics 45 65 DOI:10.1109/TCYB.2014.2319577 [Cited within:1]
18 Wei Q and Liu D 2013 IET Control Theory and Applications 7 1472 DOI:10.1049/iet-cta.2012.0486 [Cited within:1]
19 Wei Q, Liu D and Xu Y 2015 Chin. Phys. B 24 030502 DOI:10.1088/1674-1056/24/3/030502 [Cited within:1]
20 Dierks T and Jagannathan S 2012 IEEE Trans. Neural Netw. Learn. Syst. 23 1118 DOI:10.1109/TNNLS.2012.2196708 [Cited within:1]
21 Song R, Xiao W and Zhang H 2013 Neurocomputing 119 212 DOI:10.1016/j.neucom.2013.03.038 [Cited within:1]
22 Huang Y and Liu D 2014 Neurocomputing 125 46 DOI:10.1016/j.neucom.2012.07.047 [Cited within:1]
23 Xu H and Jagannathan S 2013 IEEE Trans. Neural Netw. Learn. Syst. 24 471 DOI:10.1109/TNNLS.2012.2234133 [Cited within:1]
24 Jiang Y and Jiang Z 2012 IEEE Trans. Circ. Syst. II: Express Briefs 59 693 [Cited within:1]
25 Lü J and Chen G 2002 Int. J. Bifurc. Chaos 12 659 DOI:10.1142/S0218127402004620 [Cited within:2]
26 Chen G and Ueta T 1999 Int. J. Bifurc. Chaos 9 1465 DOI:10.1142/S0218127499001024 [Cited within:1]
27 Lorenz E 1963 J. Atmospheric Sci. 20 130 DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 [Cited within:1]
28 Chua L, Komuro M and Matsumoto T 1986 IEEE Trans. Circ. Syst. 33 1072 DOI:10.1109/TCS.1986.1085869 [Cited within:1]
29 Wiggins S 1987 Phys. Lett. A 124 138 DOI:10.1016/0375-9601(87)90240-4 [Cited within:1]
30 Jiang Y and Jiang Z 2012 Automatica 48 2699 DOI:10.1016/j.automatica.2012.06.096 [Cited within:1]
31 Lü J, Chen G and Zhang S 2002 Int. J. Bifurc. Chaos 12 1001 DOI:10.1142/S0218127402004851 [Cited within:1]
32 Lü J, Chen G and Zhang S 2002 Chaos Soliton. Fract. 14 669 DOI:10.1016/S0960-0779(02)00007-3 [Cited within:1]