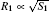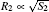†Corresponding author. E-mail: leonidmartyushev@gmail.com
The invariance of specific mass increments of crystalline structures that co-exist in the case of non-equilibrium growth is grounded for the first time by using the maximum entropy production principle. Based on the hypothesis of the existence of a universal growth equation, and through the dimensional analysis, an explicit form of the time-dependent specific mass increment is proposed. The applicability of the obtained results for describing growth in animate nature is discussed.
Interest in the study of pattern formation in the case of non-equilibrium growth (primarily, dendrite crystallization) originated long ago but remains topical. First of all, this is connected with the fact that such processes determine many properties of melt solidification. In addition to application interest, scientists studying fundamental problems of the physics of non-equilibrium processes consider dendrite growth as an important example. Based on dendrite growth, one can attempt to understand and investigate common regularities of dissipative non-equilibrium processes that generate complex structures in both animate and inanimate nature. A dependence of mass on time for these growing structures represents one of the main characteristics of a non-equilibrium system.
References [1] and [2] presented the results of experimental research on the dependence of mass on time for growing symmetrical and asymmetrical dendrites, and the so-called seaweed structures in the case of non-equilibrium crystallization of NH4Cl from a supersaturated aqueous solution. Measurements were made, both for the whole growing crystals and for their parts (for instance, separate dendrite branches). For NH4Cl crystals (and their parts) growing simultaneously and approximately at the same supersaturation (the so-called co-existing crystals), it was discovered that in spite of a significant difference in mass m and mass change rate ṁ , the values of specific mass increment ṁ /m are identical within the experimental error. It was also found that a specific mass increment can be well described by using an empirical dependence of the form (the so-called DS model[3])
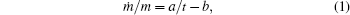
where t is the time, and a and b are the coefficients: coefficient a, according to Refs. [1] and [2], is rather universal and equals 1.8± 0.1 for all structures, coefficient b depends on the supersaturation at which the growth takes place.
The above empirical results are very surprising and interesting but they lack theoretical discussion in their original papers. The objective in this paper is to seek their explanation. Our two results are as follows: (i) it is grounded (with the help of non-equilibrium thermodynamics) that co-existing crystals have the same specific-mass increments, [4] and (ii) on the basis of the hypothesis that the dependence of specific mass increment on time is universal and through the dimensional analysis, equation (1) is grounded.
We base our reasoning on the maximum entropy production principle that is presently well-grounded and which is commonly used for thermodynamic analysis of non-equilibrium systems (see, for example, Refs. [5]– [9]). One of the principle’ s formulations applicable to the problems at hand is as follows:[10– 12] in the case of non-equilibrium growth, two co-existing structures have the same specific entropy productions.
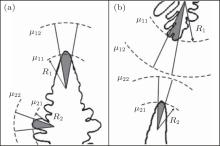
Now, we come to consider two co-existing growing crystals. Figure 1 shows two possible examples. These can be both parts of a dendrite (for example, dendritic side branches and a primary branch) and various non-equilibrium parts of crystals (e.g., a dendrite and a seaweed) growing close to each other. Their co-existence is our main requirement. Using the classical expression of entropy production as a product of crystallizing matter’ s flux and a thermodynamic force (a gradient of chemical potential), [5, 6, 8] the following can be written for the co-existing first and second part of a non-equilibrium growing crystal as
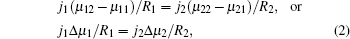
where j1 and j2 are the fluxes of a crystallizing component moving towards the boundaries of the first and the second part of the crystal, and Δ μ 1/R1 and Δ μ 2/R2 are the gradients of chemical potentials found at the distances of R1 and R2 (typical sizes of the first and the second part of the crystal, respectively; see Fig. 1). It should be noted that if condition (2) is violated, then, according to Refs. [10]– [12], one crystal (a part of a crystal) will develop considerably faster and suppress the growth of a slower crystal, and consequently, the condition of co-existence will be violated.
We can assume that the differences of chemical potentials in the vicinity of the co-existing parts are approximately equal (Δ μ 1 ≈ Δ μ 2).
Using the law of mass conservation at crystal boundaries (accurate up to a constant factor), i.e., j = ṁ /R2 (where ṁ is the change of the crystal mass m with time), the following relationship can be obtained:
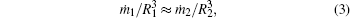
or, after dividing by crystal density, it becomes
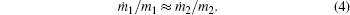
Thus, the application of the maximum entropy production principle allows us to obtain the equality of specific mass increments for different co-existing parts of a non-equilibrium growing crystal as observed in the experiment.
It is noted that a dependence of expression (4) is not only typical in the case of non-equilibrium growing crystals but is also very common in animate nature. This is the so-called law of ontogenetic allometry, stating the proportionality of relative changes in the mass values of an organism’ s growing parts. Cuvier G (1798) first suggested this law and Huxley J (1932) presented its final formulation for animate systems based on the analysis of empirical data.[13] Therefore, the above derivation of expression (4) by using common thermodynamic (rather than particular) statements is very valuable. On the other hand, equation (1) with b = 0 is also known in biology. This is the law of growth empirically obtained by Schmalhausen in 1927– 1930 through the study of embryonic growth.[14– 16] According to Schmalhausen, such a power formula provides much better results than exponential formulae. Reference [17] showed that equation (1) may also be used to describe the change of mass with time in the case of post-embryonic growth. The results obtained in the above papers make it possible to formulate a hypothesis of the existence of a universal growth equation for various objects of animate and inanimate nature which describes the change of mass with time. We try to analytically derive this equation on the basis of this hypothesis.
A system developing in time is extremely complex from morphological and kinetic perspectives. Dimensional analysis is traditionally employed to consider such complex and poorly formalized systems.[18] Using this analysis, fundamental relations between quantities that determine the process can be found correctly. Let the change of some mass with time ṁ be the main sought-for quantity in the growth equation. First of all, this quantity must be dependent on the mass m of a growing object (crystal, organism, etc.): the bigger the mass, the more it changes (in its absolute value) during growth. There are other quantities that, alongside with mass, define ṁ . We use Ω to designate a set of these quantities. Then, we remind that we have accepted the hypothesis that the law of growth is universal, i.e., growth equations for various objects (crystals, animals, plants, etc.), including those at different organizational levels (crystalline parts, plant organs, etc.), must have identical forms. Thus, no dimensional constants or variables specific for a particular growing object will appear in such a universal equation. For example, the frequency of incident radiation and the Planck constant could be important dimensional quantities for plants, and coefficients of diffusion in a medium and kinetic coefficient of crystallization could be important for crystals, etc. For the growth of one system, some dimensional quantities can be essential, whereas for the growth of other systems, they can have only secondary meaning or no meaning at all. As a result, based on the hypothesis of universality, almost all quantities that could determine growth rate in every specific case must be excluded from consideration. However, there must be a quantity with the dimension of time in Ω from the consideration of dimensionality. It seems that the time of growth (age, if the growth of animate systems is considered) is the essential quantity to select. This quantity can be introduced for any growing object; and the influence of t on ṁ is obvious.[21] Therefore, a universal equation of growth certainly contains age as the sought-for dimensional variable. Other quantities with the dimension of time can describe a change of properties in a medium of growth. Firstly, we consider the most general case where medium properties are invariable in time. This approximation evidently holds true for the very initial stage of any growth. Consequently, for this case, we draw a conclusion that ṁ is a function of m and t only, and has the following form (pursuant to the dimensional analysis):
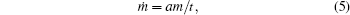
where a is some dimensionless constant.
Thus, the growth equation (5) is obtained on the basis of the dimensional analysis under the following two assumptions: i) an equation of growth is universal for various objects (of both animate and inanimate nature); and, ii) a change in a medium can be neglected.
Equation (5) can be easily specified for the case of changing growth conditions. We can make the simplest assumption that the changes in a medium occur due to the growth itself and they are proportional to the mass of a growing body only. Hence, equation (5) can be rewritten as follows:
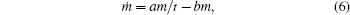
where b is some positive constant having the dimension of reverse time. This dependence conforms to the DS model (1) that was empirically proposed earlier.
Thus, using the maximum entropy production principle, the hypothesis of the existence of a universal growth equation, and the dimensional analysis, the invariance of specific mass increments for growing co-existing structures is grounded and its explicit form that has been empirically obtained many times for growing objects of animate and inanimate nature is derived analytically in this paper.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|