One-dimensional (1D) quantum gas is a popular platform to simulate quantum many-body physics of strongly correlated low-dimensional quantum systems. Its availability in experiment has attracted great theoretical and experimental interest. With highly anisotropic magnetic trap and optical lattice, the low-dimensional quantum gas can be realized and controlled.^{[1– 5]} The strongly interacting Bose gas, Tonks– Girardeau gas, ^{[6– 8]} can be realized with Feshbach resonance technique or confinement-induced resonance, while the highly excited quantum gas, super-Tonks– Girardeau gas, ^{[9– 14]} can also be realized by a sudden quench of interaction. Recently, Jacqmin et al. realized a single 1D Bose gas with strong interaction, which allows us to measure the atom number fluctuation locally and opens more opportunities to investigate the properties related to temperature effect.^[5]

Theoretically, the strongly correlated 1D quantum gas has been the center of research topics. It is shown that with the increases in interaction and temperature, the 1D Bose gases exhibit different properties. Based on two-body correlation, the Bose gas can be classified into various physical regimes.^{[15– 17]} In weak interaction regime, the Bose gas can be described approximated by mean field theory, ^[18] while in strong interaction regime we must turn to exact non-perturbation methods, such as Bethe ansatz^{[19– 23]} and exact diagonalization.^{[24– 26]} The ground state of Bose gas exhibits the Fermi-like density distribution, although the momentum distribution still behaves like Bose system.^[20] The ground state of Bose gas in different interacting regimes has been studied widely. The Bose gas at finite temperature has been paid little attention although the temperature effect is important for quantum gas. The recent research showed that the universal contact of Tonks gas depends on temperature.^[5]

In this paper, we investigate the Tonks– Girardeau gas trapped in a harmonic trap at finite temperature. With thermal Bose– Fermi mapping method, we obtain density profiles and the reduced one-body density matrix.

We consider a system of N Bose atoms with δ interaction in a one-dimensional harmonic trap V(x) = mω ²x²/2, with m being the atom mass. The Hamiltonian can be formulated as

where g_1D is the effective one-dimensional interaction constant given by^{[27, 28]}

where a_s is the s-wave scattering length, 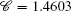, and , with ω _⊥ being transverse trapping frequency. The effective one-dimensional interaction can be tuned experimentally from the weak interaction to strong interaction by changing the transversal trapping frequency ω _⊥ and the s-wave scattering length a_s with Feshbach resonance technique. The Tonks– Girardeau gas corresponds to the strong interaction limit g^1D → ∞ , and its eigen wavefunction ψ ^b(x₁, x₂, ..., x_N) can be exactly obtained from the wavefunction of N polarized free fermions ψ ^f(x₁, x₂, ..., x_N) with the Bose– Fermi mapping method^{[29, 30]}

Here the function A is the product of a series of sign function sign(x)

and sign(x) is + 1, 0, and − 1, corresponding to positive, zero, and negative x, respectively. The above mapping holds as the wavefunction satisfies the boundary condition ψ (x₁, ..., x_i, ..., x_j, ..., x_N) = 0 for x_i = x_j. Further the eigen energy of Tonks gas is identical to the energy of corresponding free Fermion gas. 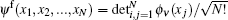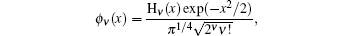It is well known that the many-body wavefunction of N free Fermions is Slater determinants of single-particle wavefunction ϕ _ν (x). For the particle confined in harmonic trap, the single-particle wavefunction

with Hermite polynomial

The Bose– Fermi mapping method can be utilized to construct both the wavefunction of the ground state and the wavefunction of arbitrary eigenstate of H, with g_1D → ∞ , which satisfies the eigen equation

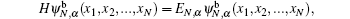
where α denotes the corresponding quantum number {ν ₁, ν ₂, ..., ν _N}, and the eigen energy . For a statistical mechanical ensemble of Bosons, every eigenstate should be attached with a probability P_{N, α} which takes the form of

with Z being the partition function, β = 1/k_BT, and μ chemical potential. According to Eq.  (2), the properties of Tonks gas depending only on the absolute value of wavefunction are the same as those of polarized free Fermions. While the properties depending on wavefunction are distinct from each other. In this paper we will investigate the reduced one-body density matrix ρ ^b(x, y) defined as^[29]

where x and y may be any value of one-dimensional coordinate system. Here α sums over all possible occupation configurations, i.e., {ν ₁, ν ₂, ..., ν _N} includes all permutations of N dimension of {0, 1, ..., M}. For the ground state, the N Bosons occupy the lowest N single-particle eigenstates of harmonic potential and M = N. At finite temperature, the Tonks gas satisfy Fermi– Dirac distribution (i.e., f_ν = e^{− β (ε _ν − μ )}), and Bosons will occupy higher eigenstates (M > N). In the calculations, we will ignore the high eigenstates with negligible f_ν .

To calculate the reduced one-body density matrix, we insert Eq.  (2) into Eq.  (4), and it turns out that ρ ^b(x, y) is related to the fermion density matrix ^[29]

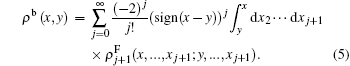
The above integration formally is multiple integral and usually is difficult to be evaluated. In the present calculation, the (j+ 1)-body Fermion density matrix can be factorized into (j+ 1)-dimensional determinant of one-body Fermion density matrix as follows:^[29]

Based on the properties of determinants, the multiple integral can be reduced into single-variable integrals^[31]

As the temperature is high enough, the one-body Fermion density matrix is approximate to^[31]

with C = exp[β (μ − ħ ω /2)]/[π (1 − e^{− β ħ ω} )]².

For simplicity, we will take the oscillator length as the length unit, and ħ ω as the temperature unit. In Fig.  1, we show the density profiles of Tonks gas ρ (x) at different temperatures, which is the diagonal element of the reduced one-body density matrix, i.e., ρ (x) = ρ ^b(x, x). It is shown that as the temperature is low enough, the density profiles display the Fermi-like shell structures, which is the same as the ground-state density profiles, ^[20] and the Bosons mainly distribute in the central region of the trap. As temperature increases, the shell structures disappear and Bose atoms will distribute in wider regions. At low temperature, N Bose atoms occupy the lower single-particle eigenstates with larger probabilities, and obvious shell structures are exhibited. At high temperature, the probability that atoms occupy the lower eigenstates becomes small, and the higher eigenstates shall be occupied with larger probabilities. Because the high eigenstates' wavefunctions are wider, the density profiles of Tonks gas become wide at high temperature. Since the density distributions of Tonks gas depend on the absolute value of wavefunction, we cannot distinct Bosons from Fermions by them.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Density distribution of the 1D Bose gas in a harmonic trap with N = 4. The length is in unit of harmonic oscillator length a0.

In Fig.  2 we display the dimensionless reduced one-body density matrix ρ ^b(x, y) for T = 0.1, 0.5, 1.0, and 10.0. It is shown that the reduced one-body density matrix is diagonal dominant for both low temperature and high temperature. With the increase in temperature, the off-diagonal elements decrease in contrast to the diagonal, and disappear completely when the temperature is high enough. The former relates to the off-diagonal long-range order.^[32] This indicates that the off-diagonal long-range order vanishes at high temperature. Actually both the diagonal part of the reduced one-body density matrix and the whole part decrease when the temperature becomes high. In order to clarify this more clearly, we fix x at the

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Reduced one-body density matrix of Bosons in a harmonic trap with N = 4. (a)T = 0.1; (b)T = 0.5; (c)T = 1.0; (d)T = 10.0. The temperature is in unit of ħ ω .

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Reduced one-body density matrix ρ (0, y) as a function of the displacement from the trap center. The length is in unit of harmonic oscillator length a0.

trap center and investigate the properties of the reduced one-body density matrix. The ρ ^b(0, y) for different temperatures is shown in Fig.  3. At low temperature, the value of ρ (0, y) in the trap center region do not change obviously, and the temperature effect is not obvious. As temperature increases, ρ (0, y) can decrease in the whole trap and decrease to zero rapidly in the region away from the trap center. The temperature effect on the off-diagonal long-range order of Tonks gas is obvious, while the temperature effect of the diagonal part of reduced one-body density matrix is shown obviously only at higher temperature.

In this paper, with thermal Bose– Fermi mapping method we investigate the Tonks gas at finite temperature. The density profiles and the reduced one-body density matrix are evaluated in the whole temperature region. It is shown that at low temperature the density profiles show the Fermi-like properties and Bosons shall distribute in wider region with the increase in temperature. The reduced one-body density matrix is diagonal dominant in the whole temperature region, and the off-diagonal part shall vanish completely at high temperature.