A variety of exotic phenomena in condensate matter systems have their physical origin related to the electrons experienced by an external gauge field or in the presence of spin– orbit coupling (SOC), which is crucial for quantum spin Hall effect, topological insulators and superconductors.^{[1– 4]} Neutral atoms originally do not have SOC effect, however, in the past few years synthetic SOC has been generated for ultracold atoms by engineering atom– light interactions.^{[5– 10]} In fact, quantum gases are good candidates to investigate the interplay between interaction and SOC in many-body systems and exotic quantum phases have been observed with Bose– Einstein condensates (BECs) and degenerate Fermi gases.^{[11– 19]} Furthermore, rich ground-state phases such as meron spin configuration and quantum quasicrystals have been predicted in dipolar spin– orbit-coupled gases.^{[20, 21]} In the present work we are instead interested in the ground-state properties of quantum gas under the effects of long-range interaction and synthetic gauge fields. Recently, great achievements have been made in manipulating the atoms several micrometers apart by engineering long-range interactions especially when the atoms are excited to a high-lying Rydberg state.^{[22– 25]} Strong van der Waals (vdW) interaction between Rydberg states and off-resonant coupling between ground and Rydberg states lead to Rydberg-dressing interaction subject to degenerate quantum gases, which may lead to the supersolidity of the dressed gas as a result of roton minimum and blockade effect.^{[26, 27]} Moreover, dipole-mediated energy transport by Rydberg interaction^[28] and spatially ordered excitations^[29] have been observed recently, which demonstrate the potential of Rydberg gases to realize exotic phases of matter, thereby paving the way for quantum simulations of strongly correlated systems with long-range interactions.

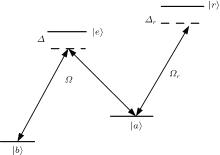
We consider a Bose– Einstein condensate (BEC) of rubidium atoms with a Λ -type Raman-transition configuration, as shown in Fig. 1. Two spin states | a⟩ = | 5S_1/2, F = 1, m_F = 0⟩ and | b⟩ = | 5S_1/2, F = 1, m_F = − 1⟩ are coupled to an excited state | e⟩ respectively by 804-nm Raman beams which intersect at the angle 90° .^[6] The recoil energy is E_r = h × 1.77 kHz. In order to introduce the long-range interaction, we couple the state | a⟩ to a high-lying Rydberg state | r⟩ via a two-photon process (for example, choosing | 43S_1/2⟩ state as the states | r〉 and | 5P_3/2〉 as the intermediate state). Effective Rabi frequencies and the detunings of the Raman and Rydberg transitions are Ω , Ω _r, Δ , and Δ _r, respectively. In the off-resonant coupling regime, i.e., Δ _r ≫ Ω _r, the Rydberg state | r〉 can be adiabatically eliminated, which results in an effective soft-core interaction with for the | a〉 atoms and the blockade radius R_c = (| C₆| /2ħ | Δ _r| )^1/6 gives the strength of vdW interaction in the Rydberg state (C₆ is the vdW coefficient).^[26] The laser detuning from the 5P_3/2 state was 400 MHz, giving the blockade radius R_c = 1.6 μ m.^[30] Generally, Rydberg-dressing interaction is repulsive for a high-lying s-state, ^[31] however, it can be attractive if we choose a Rydberg d_3/2-state with n ≥ 59.^[32]

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Level scheme of atoms imposed by a two-photon Raman-induced SOC and a Rydberg-dressing interaction. Two spin states | a〉 and | b〉 are coupled by counter-propagating Raman lasers. The atoms in the state | a〉 interact with each other by a long-range Rydberg-dressing potential, which can be realized by an effective off-resonant Rydberg transition.

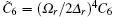
Considering an interacting spin-1/2 BEC in Fig. 1, we have the mean-field energy functional (we set ħ = m = 1)

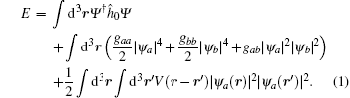
Here, Ψ = (Ψ _a, Ψ _b)^T is the two-component condensate wavefunction. The inter- and intra-component interactions are characterized by the coupling strengths g_ij = 4π a_ij (i, j = a, b) with a_ij the corresponding s-wave scattering lengths. The first term corresponds to Raman-induced SOC Hamiltonian

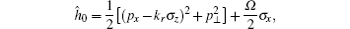
with the Pauli matrices σ _{x, y, z} and k_r the wave vector. For Ω < 4E_r, degenerate minima appear in the dispersion relation capable of hosting a condensate with 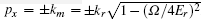, E_r being the recoil energy. Furthermore, k_m vanishes for Ω ≥ 4E_r and all the atoms occupy the single-momentum state with p_x = 0. The second term in Eq. (1) includes inter- and intra-component s-wave scattering interactions between the atoms. Different from the previous works, we introduce a long-range and soft-core Rydberg interaction between the atoms only in the state | a〉 by coupling to the Rydberg state | r〉 . In fact, one of the ground states becomes an admixture of | a〉 and | r〉 when the Rydberg-dressing interaction works. However, since Ω _r ≪ Δ _r, the Rydberg state with the population p_r ∼ (Ω _r/2Δ _r)² can be ignored. We assume that all atoms are in the ground states and apply the mean field approximation to the Rydberg-dressing interaction.

In general, the ground-state wavefunction can be determined by minimizing the total energy Eq. (1) with the following ansatz:^{[33, 34]}

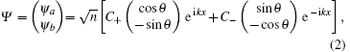
where n is average density and k ≥ 0, C_± , θ , and k are variational parameters and the normalization constraint | C₊ | ² + | C₋ | ² = 1 should be satisfied. A general relation cos(2θ ) = k/k_r is fixed by minimizing the single-particle Hamiltonian ĥ ₀ with respect to k. Using Eq. (2), one can calculate spin polarization as ⟨ σ _z〉 = n(| C₊ | ² − | C₋ | ²)/(k/k_r). Substituting Eq. (2) into Eq. (1), we obtain the mean energy ε = ε ₀ + ε _ryd per atom

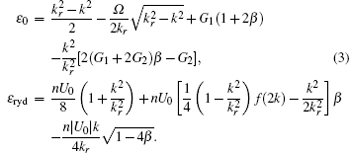
Here, we have defined the quantities G₁ = n(g + g_ab)/4, G₂ = n(g − g_ab)/4, and β = | C₊ C₋ | ². The ε ₀ represents the mean energy contributed from the SOC and atomic s-wave interactions, while ε _ryd is the Rydberg-dressing interaction. U(k) = U₀f(2k) with U(0) = U₀ is Fourier transformation of the soft-core interaction V(r), given by

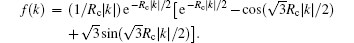
As is well known, distinct quantum phases emerge without the Rydberg interaction, depending on the values of the relevant parameters k_r, Ω , g_ij, and n. For small values of Ω and G₂ > 0, the condensation hosts the superposition of two plane-wave (PW) states e^{± ikx} with equal weight (β = 1/4 and 〈 σ _z〉 = 0) characterized with density-modulated stripes. This is so-called standing-wave (SW) or stripe phase.^{[33– 36]} For larger values of the Raman coupling, the condensate is in a single PW state with a finite momentum (i.e., p_x = ± k ê _x with β = 0 and 〈 σ _z〉 ≠ = 0). At even larger Ω , the degenerate momenta merge and zero-momentum phase forms spontaneously.^[36]

From now on, we are interested in the effects of the long-range Rydberg-dressing interaction on the ground-state quantum phases of the spin– orbit coupled atomic gases. Firstly we consider the simplest case with symmetric s-wave interaction strengths, i.e., G₁ = ng/2 and G₂ = 0. By using the variation method, we find that the ground state requires β = 0 and the mean total energy reduces to

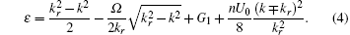
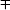
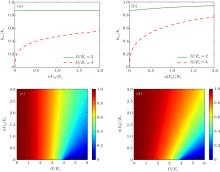
Here, correspond to repulsive (U₀ > 0) and attractive (U₀ < 0) Rydberg-dressing potentials. One can immediately find that the single-particle and Rydberg-dressing interaction is dependent on the momentum of the BEC.

For example, we choose two cases with Ω = 2E_r, 4E_r and give the values of k_m as a function of the Rydberg interaction strength in Fig. 2. Since in this situation the s-wave interactions are SU(2)-invariant, the s-wave interaction energy is momentum-independent now. The ground state is totally determined by the single-particle and Rydberg-dressing interactions. In the case of the repulsive Rydberg interaction, for a small Ω , there are two minima of the energy and the ground state of the condensate is still in the PW phase. With increasing U₀, k_m grows slightly. When the Rydberg interaction is attractive, however, k_m grows obviously but no more than k_r. For a large Ω , an intriguing feature is that the zero-momentum phase is energetically unfavorable and the PW phases with ± k_m emerge since Z₂ symmetry is broken by the Rydberg interaction. For Ω ≥ 4E_r, we can see from Eq. (4) that ε ₀ has a minimum at k = 0 while ε _ryd has a maximum at k = 0. Therefore the total energy has its minimum at a point with k_m > 0 to make ε as small as possible. If U₀ = 8E_r, k_m can be calculated exactly as , which is not equal to zero obviously.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The momentum of the ground-state wavefunction as a function of Rydberg-dressing interaction strength ((a) and (b)) and spin polarization | 〈 σ z〉 | ((c) and (d)) versus nU0 and Ω for repulsive ((a) and (c)) and attractive ((b) and (d)) cases. The parameters are Ω /Er = 2 (green solid), 4 (red dashed), and G1 = 0.4Er, G2 = 0.

Once the ground-state wavefunction is obtained, the spin polarization | 〈 σ _z〉 | can be easily extracted as shown in Figs. 2(c) and 2(d). It is obvious that the gas is always magnetic for U₀ ≠ 0 even for large Ω in both of the repulsive and attractive Rydberg interaction cases. In particular, when Ω > 4E_r, an unexpected transition from the non-magnetic phase to the magnetic phase is revealed, which is absent for an s-wave interacting spin– orbit coupled atomic gas. At this time, the system is in the PW phase and | 〈 σ _z〉 | is equal to k_m/k_r since β = 0, so we always have | 〈 σ _z〉 | ≠ 0 since k_m changes to be non-zero as illustrated above.

Now we are in the position to analyze the interesting G₂ > 0 case, for example, G₁ = 0.4E_r and G₂ = 0.1E_r. Without the Rydberg-dressing interaction, the system undergoes phase transition between three distinct phases at two critical values as varying Ω . The system is in the SW phase when Ω < Ω ₁ = 2.4E_r and in the zero-momentum phase for Ω ≥ Ω ₁ = 3.6E_r, in which the spin polarization of the condensate is zero, while the condensate is in the separated PW phase with non-zero 〈 σ _z〉 for a moderate Ω ∈ (Ω ₁, Ω ₂).^[33] In Fig. 3 we plot the ground-state phase diagram and spin polarization for both the repulsive and attractive Rydberg interactions. For large Ω , whether repulsive or attractive, the system is always in the PW phase and | 〈 σ _z〉 | proportional to k_m grows with increasing | U₀| . Especially when Ω ≥ 4E_r, similar to the case of G₂ = 0, the energy evolves continuously from having single minimum (zero-momentum) to having two degenerate minima as increasing | U₀| . Accompanied with the PW phase, the system becomes magnetic. The reason is the same as that of the G₂ = 0 case.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Ground-state phase diagrams ((a) and (b)) and spin polarization | 〈 σ z〉 | ((c) and (d)) for the repulsive ((a), (c), and (e)) and attractive ((b), (d), and (f)) Rydberg-dressing interactions, respectively. The spin polarization | 〈 σ z〉 | ((e) and (f)) at Ω /Er = 2 (green solid), 3 (blue dashed), and 4 (red dotted). Other parameters are G1 = 0.4Er, G1 = 0.1Er, and Rc = 1.6 μ m.

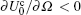
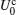
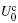
Next we focus on the interesting small Ω case in which the system should be favourable with the non-magnetic SW phase for U₀ = 0. The ground-state phase diagrams are shown in Figs. 3(a) and 3(b). For U₀ > 0, with increasing U₀, the phase boundary between the SW and PW phases bends to small Ω because we find on the boundary of the SW and PW phases ( is the critical value of U₀ at the phase transition points). Therefore strong Rydberg interaction is required to observe the phase transition with very small Ω . We also find that does not become a finite value when Ω approaches to zero. The SW phase always emerges spontaneously in the regime of weak SOC. However, the PW phase predominates and the SW phase is totally suppressed for U₀ < 0. The critical value of n| U₀| continually approaches to the maximum 4G₂ when Ω approaches to zero. It is clearly shown that the system is favourable to form the PW phase especially imposed by strong Rydberg interaction. The spin polarization is depicted in Figs. 3(c) and 3(d) and the boundary of the SW phase and the PW phase is also remarkably visible. Particularly, the SW phase is not always non-magnetic with equal weight for each momentum component in the presence of the Rydberg interaction. For both the repulsive and attractive Rydberg interaction cases, | 〈 σ _z〉 | is increasing as | U₀| grows if the gas is in the SW phase.

To analyze the influence of the Rydberg-dressing interaction, we fix the values of Ω and calculate the spin polarization as a function of Rydberg-dressing interaction strength as shown in Figs. 3(e) and 3(f) respectively. For Ω = 2E_r, | 〈 σ _z〉 | jumps up abruptly, which indicates the phase transition from the SW phase to the separated PW phase. The phase transition is first-order because | 〈 σ _z〉 | can be treated as an order parameter^[19] and is not a continuous function of U₀. Particularly, in the SW phase | C₊ | ² ≠ | C₋ | ² with 0 < β < 1/4 and the condensate becomes magnetic, which can only be attributed to the Rydberg interaction. Since n_a = | Ψ _a| ² = n[| C₊ | ² cos(2θ ) + | C₋ | ² sin(2θ )] is proportional to 1 − | 〈 σ _z〉 | , the | a〉 atoms experienced by the Rydberg-dressing potential tend to transfer to the state | b〉 to reduce the total energy. Once n| U₀| exceeds a critical value, the system enters the magnetic PW phase with the momentum k_m or − k_m. For the cases of Ω = 3E_r and Ω = 4E_r, the gas is always in the magnetic PW phase and the spin polarization of the BEC increases with increasing | U₀| . At this time, the phase transition hardly happens. When Ω ≥ Ω ₂ = 3.6E_r, however, the Rydberg interaction inhibits the emergence of the zero-momentum phase and maintains the separated PW phase.

In summary, we have explored the ground-state properties of the Rydberg-dressing BEC imposed by synthetic Raman-induced SOC. In the case of SU(2)-invariant s-wave interactions, for large Ω , the zero-momentum phase is completely suppressed because it is unfavorable in energy compared to the separated PW phase in the presence of the k-dependent long-range Rydberg interaction. This feature also happens in the situation of non-symmetric s-wave interactions. Furthermore, an unexpected magnetic SW phase emerges with small Ω , which arises from the Rydberg-dressing interaction. We remark that the stability and excitation properties of the Rydberg-dressed condensate with SOC are further expected to investigate, and the effect of the long-range Rydberg-dressing potential with the roton nature on the unique stripe phase is particularly significant for potential applications. Our work may provide new insights into quantum gases with synthetic gauge field and long-range interaction.