Quantum teleportation, quantum key distribution, quantum dense coding, and quantum secret sharing are foundational schemes for quantum communication, which have been presented in different quantum physical systems.^{[1– 7]} It is commonly believed that the entanglement which is a nonclassical and nonlocal correlation, is responsible for these possibilities. Wootters^[8] introduced the concurrence (C) to calculate the entanglement of two-qubit system. In addition, there are other quantum correlations, which have been discussed widely and found to be useful in some quantum information applications. Quantum discord (QD) is one among them, ^{[9, 10]} which measures a more general type of quantum correlation and is found to have nonzero values even for separable mixed states. Generally, it is somewhat difficult to calculate QD and the analytical solutions can be hardly obtained except for some particular cases, such as the so-called X states.^[11] Some research showed that the QD, C, and classical correlation (CC) are independent measurements of correlations with no simple ordering, and QD is more practical than entanglement.^[12] Moreover, Dakić et al. have introduced an easily analytically computable quantity, geometrical measurement of quantum discord (GQD), ^[13] and have given a necessary and sufficient condition for the existence of nonzero QD for any dimensional bipartite states. However, real quantum systems will unavoidably be influenced by the surrounding environment, which leads to decoherence. Although the dynamical behavior of QD is studied in terms of decoherence^{[14– 16]} in both Markovian^[17] and non-Markovian^{[18– 20]} cases, the influence of intrinsic decoherence on various correlations is seldom discussed.^[21]

Quantum dense coding, as a fascinating feature of quantum information, has been one of the hot topics since its first proposition by Bennett and Wiesner.^[4] In the original protocol, two bits of classical information can be transmitted by sending only one qubit if the two parties share a two-qubit maximally entangled state (EPR state). From then on, piles of works on dense coding have been presented theoretically and experimentally. In 1996, Mattle et al.^[22] experimentally demonstrated quantum dense coding with two polarized and entangled photons.

In recent years, there have been many reports about the superconducting quantum circuits that have been used in quantum information science.^{[23– 26]} This is due to the fact that compared with the other physical systems that have been suggested as possible approaches to realize qubits, the superconducting circuits are more easily embedded in electronic circuits and scaled up to larger registers.^[27] Particularly, the charge qubit as one of the basic elements, which can be conveniently addressed by the external parameters, such as gate voltages and magnetic fluxes, has attracted considerable attention in the past decade.^{[28– 30]} Many studies about the entanglement properties of the superconducting-charge-qubit system have been done.^{[30– 35]} For example, reference [31] discussed the entanglement property of the model, which is composed of two coupled superconducting charge qubits by connecting a large Josephson junction; reference [33] studied the creation and evolution of quantum entanglement in two charge qubits coupled by a nanomechanical resonator system. It was indicated in Ref. [34] that the maximum value of concurrence of two identical charge qubits is much larger than two different charge qubits coupled by a fixed capacitor. The entanglement of two charge qubits produced in a damped cavity has also been reported.^[36]

In this paper, based on the outline presented above, we will discuss the influence of intrinsic decoherence on various correlations and dense coding in the model of two superconducting charge qubits coupled by a fixed capacitor. The joint effects of intrinsic decoherence, the Josephson energy, and the mutual coupling energy between the two charge qubits on various correlations and dense coding are investigated. Our concern with the interplay between the intrinsic decoherence and system parameters for the correlation dynamics and dense coding will help us clarify the possibilities of fighting against the phase decoherence in increasing the correlations and implementing high quality dense coding.

This paper is organized as follows. In Section 2, we introduce the model and the definitions of correlations. In Section 3, we study the influence of intrinsic decoherence on various correlations of the model. In Section 4, the dense coding of the model under intrinsic decoherence is investigated. Finally, a brief conclusion is made in Section 5.

A superconducting charge qubit is composed of a Cooper-pair box, a tunnel Josephson junction and a superconducting electrode, in which the charge energy (E_C) dominates the Josephson energy (E_J). In order to control the interactions between two charge qubits, one possibility is to connect them via a capacitor which allows an easy realization of a CNOT gate.^[27] The Hamiltonian for this kind of interaction is an Ising-type coupling term σ _z ⊗ σ _z and the thermal entanglement of this system has been reported.^[34] Then, one can write the Hamiltonian of the two superconducting charge qubits system as

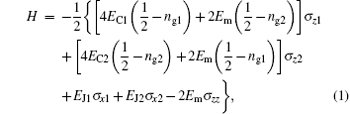
where E_Ci and E_Ji are the charging and Josephson energy of the i-th charge qubit, respectively; E_m is the mutual coupling energy between the two qubits; σ _x1 = σ _x ⊗ I, σ _x2 = I ⊗ σ _x, σ _z1 = σ _z ⊗ I, σ _z2 = I ⊗ σ _z, σ _zz = σ _z ⊗ σ _z, in which σ _x and σ _z are the normal Pauli matrices and I is the identity matrix; n_gi = C_giV_gi/2e is the normalized qubit gate charge, where C_gi and V_gi are the control gate capacitance and voltage, respectively. We consider a simple but nontrivial form of Eq. (1), where n_g1 = n_g2 = 1/2, i.e., the degeneracy point, which is the condition of insensitivity to fluctuations in the external parameters.^[37] Under this condition, the model Hamiltonian is reduced to

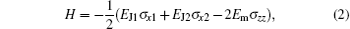
which can be written in the matrix form on the standard basis as

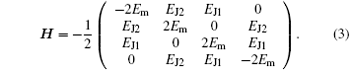
We can see that the Hamiltonian is independent of the charging energy E_C in this case. Due to the fact that the entanglement resource as well as the quantum discord between two identical charge qubits is much richer than that of different qubits, ^{[36, 38]} we will focus on the case of qubits with the same system parameters, i.e., E_J1 = E_J2 = E_J and E_C1 = E_C2. The model Hamiltonian can then be rewritten as

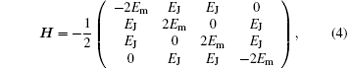
where E_J and E_m can be adjusted by the experimental multiplexed capacitance in the circuits.

Let us now recall the original definitions of QD, CC, C, and GQD. In the classical information theory, the total correlation in a bipartite quantum system (A) and (B), measured by the quantum mutual information, is defined as

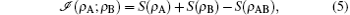
where ρ _A(B) = Tr_B(A)(ρ _AB) is the reduced density matrix of the subsystem A(B) by tracing out the subsystem B(A). The quantum generalization of the conditional entropy is not the simple replacement of Shannon entropy with von Neumann entropy, but through the process of projective measurement on the subsystem B by a set of complete projectors B_k, with the outcomes labeled by k, then the conditional density matrix ρ _k becomes

which is the local post-measurement state of the subsystem B after obtaining the outcome k on the subsystem A with the probability

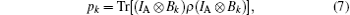
where I_A is the identity operator on the subsystem A. The projectors B_k can be parameterized as B_k = V| k⟩ ⟨ k| V^† , k = 0, 1 and the transform matrix V ∈ U(2) (in Ref. [39]) is

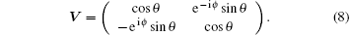
Then the conditional von Neumann entropy (quantum conditional entropy) and quantum extension of the mutual information can be defined as^[9]

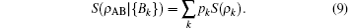
Following the definition of the CC(ρ _AB)^[9]

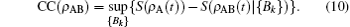
Then QD(ρ _AB) defined by the difference between the quantum mutual information I(ρ _AB) and the CC(ρ _AB) is given by QD(ρ _AB) = _I(ρ _AB) − CC(ρ _AB). Then a variant expression of CC(ρ _AB) and QD(ρ _AB) is given by ^{[9, 10]}

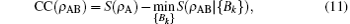
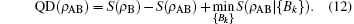
For a pair of qubits, the concurrence introduced by Wootters, ^[8] the concurrence is defined as: C(ρ _AB) = max[λ ₁ − λ ₂ − λ ₃ − λ ₄, 0], where the quantities λ ₁ ≥ λ ₂ ≥ λ ₃ ≥ λ ₄ are the square roots of the eigenvalues of the matrix product 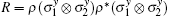in descending order. The ρ is the density operator of the pair and it can be either pure or mixed. The nonzero concurrence implies that the qubits 1 and 2 are entangled. Entanglement of formation is a monotonically increasing function of C(ρ _AB). The concurrence C(ρ _AB) = 0 corresponds to an unentangled state and C(ρ _AB) = 1 corresponds to a maximally entangled state.

There exists an analytic expression about geometrical measure of quantum discord for any quantum state of a two-qubits system and more general quantum state of dimensional.^{[13, 40]} There exists a Bloch expression for any quantum state of two qubits system as follows:^[41]

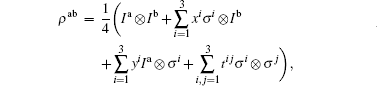
where xⁱ = Trρ (σ ⁱ ⊗ I^b), yⁱ = Trρ (I^a ⊗ σ ⁱ), t^ij = Trρ (σ ⁱ ⊗ σ ^j), x ≔ (x₁, x₂, x₃)^t, and y ≔ (y₁, y₂, y₃)^t are the Bloch vectors of edge states ρ ^a and ρ ^b, but T ≔ t_ij is the correlation matrix of two body quantum states. Then the geometric quantum discord of ρ ^ab is

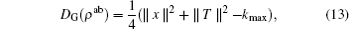
where k_max is the largest eigenvalue of the matrix K = xx^t + TT^t.

According to Milburn’ s equation^[42] followed by the assumption that a system does not evolve continuously under unitary transformation for sufficiently short time steps, the master equation for pure phase decoherence is given by

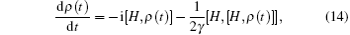
where γ is the phase (intrinsic) decoherence rate, which is responsible for the decay of quantum coherence in the energy eigenstate basis, without the usual energy dissipation associated with the normal decay. The formal solution of the above master equation can be expressed as^{[42– 47]}

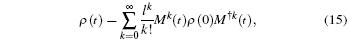
where ρ (0) is the density operator of the initial system and M^k(t) is defined by

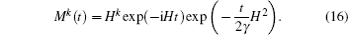
By inserting the completeness relation Σ _n | ψ _n⟩ ⟨ ψ _n| = I of the energy eigenstate into the master equation, ^[43] the time evolution of the density operator for the system mentioned above can be given by

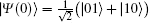
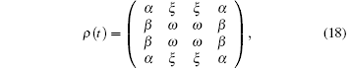
where E_{m, n} and ψ _{m, n} are the eigenvalues and the corresponding eigenvectors, respectively. We assume that the system is initially prepared in the Bell state . From Eq. (16), the time evolution of ρ (t) for this initial state of the system can be obtained as

where

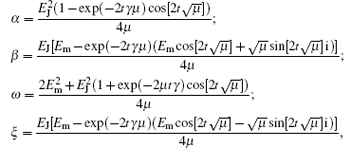
where .

Based on the definitions of C, CC, QD, and GQD, and Milburn’ s method for the description of the intrinsic decoherence, we will present a brief analysis on the correlation dynamics with the corresponding plots in the following.

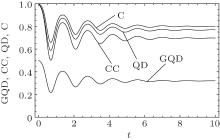
From Fig. 1, it is easy to find that all the correlations finally reach their steady state values after some oscillations. That is, for the system parameters chosen as in the figure caption, the correlations may evolve into finite steady state values despite the intrinsic decoherence. The robustness of the correlations may be ranked in the order of C, QD, CC, and GQD.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Correlations versus t with EJ = 1, Em = 2, and γ = 0.05.

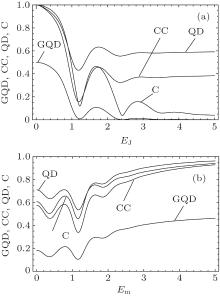
To examine the effects of system parameters E_J and E_m on the correlation dynamics under phase decoherence, we give the plots in Fig. 2(a) (Fig. 2(b)) for the correlations versus E_J (E_m), with the other parameters fixed. Overall, the smaller E_J and the larger E_m may result in larger correlations. The rank of the steady state values of the correlations in Fig. 2(b) is the same as that in Fig. 1, while it is somewhat different in Fig. 2(a) in that QD is the highest instead of C. Again, the E_m may be used as an effective system parameter against the intrinsic decoherence in increasing the correlations.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) Correlations versus EJ with Em = 1, t = 3, and γ = 0.05; (b) correlations versus Em with EJ = 1, t = 5, and γ = 0.05.

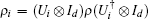
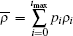
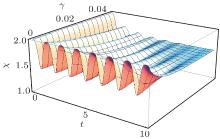
In the general dense coding, the sender performs one of the local unitary transformations U_i ∈ U(d) on d-dimensional quantum system to put the initially shared entangled state ρ in with a priori probability p_i (i = 0, 1, … , i_max), and then the sender sends off his quantum system to the receiver. Upon receiving this quantum system, the receiver performs a suitable measurement on ρ _i to extract the information. The optimal amount of information that can be conveyed is known to be bounded from above by Holevo quantity^[48]χ = S(ρ ) − S(ρ ), where S(ρ ) = − Tr(ρ log₂ρ ) denotes the von Neumann entropy and is the average density matrix of the signal ensemble. Since the Holevo quantity is asymptotically achievable, ^{[49, 50]} one can use χ = S(ρ ) − S(ρ ) as the definition of the capacity of dense coding.

At the next step, we discuss the dense coding by using the entangled states of the above model as a channel and give the intuitional description of the influence of the intrinsic decoherence on dense coding channel capacity in terms of a three-dimensional diagram. From Fig. 3, it can be seen that the dense coding channel capacity χ oscillates periodically with the time for the small phase decoherence rates. As the decoherence effect increases, although the oscillatory behavior of the χ suffers a significant suppression, it approaches a final steady state value, which allows a valid dense coding.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Dense coding capacity χ versus t and γ with EJ = 2 and Em = 1.

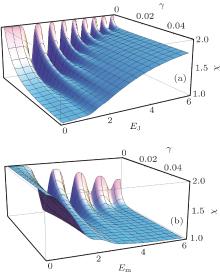
In order to examine the combinatory effects of E_J, E_m, and γ on the dense coding capacity, we give the plots χ versus E_J and γ , and χ versus E_m and γ in Figs. 4(a) and 4(b), respectively. The evolution time is long enough to guarantee χ to reach its final steady state value. It is found that the roles of the Josephson energy and mutual coupling energy in fighting against the intrinsic decoherence are opposite in that the smaller Josephson energy leads to the larger capacity, while the larger mutual coupling energy leads to the larger capacity. That is to say, the final steady state value of the dense coding capacity is still high despite the phase decoherence, implying that the χ can still be kept highly immune to the decoherence via increasing the mutual coupling energy and/or decreasing the Josephson energy.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (a) Dense coding capacity χ versus EJ and γ with t = 5 and Em = 0.7; (b) dense coding capacity χ versus Em and γ with t = 6 and EJ = 2.

In conclusion, we have examined the influence of intrinsic decoherence on various correlations in the model of two superconducting charge qubits coupled via a fixed capacitor. The results show that despite the phase decoherence all the correlations reach their steady state values after exhibiting some oscillations. The joint effects of the Josephson energy, mutual coupling energy between the charge qubits, and the intrinsic decoherence on the correlations and dense coding channel capacity are investigated. Importantly, for the model under consideration, it is possible to increase the correlations and the dense coding channel capacity via an appropriate combination of system parameters, in which the Josephson energy is smaller than the mutual coupling energy between the two charge qubits.