†Corresponding author. E-mail: lihw@mail.ustc.edu.cn
‡Corresponding author. E-mail: yinzheqi@mail.ustc.edu.cn
*Project supported by the National Basic Research Program of China (Grant Nos. 2011CBA00200 and 2011CB921200), the National Natural Science Foundation of China (Grant Nos. 61475148, 61201239, 61205118, and 11304397), and the China Postdoctoral Science Foundation (Grant No. 2013M540514).
In a practical quantum key distribution (QKD) system, imperfect equipment, especially the single-photon detector, can be eavesdropped on by a blinding attack. However, the original blinding attack may be discovered by directly detecting the current. In this paper, we propose a probabilistic blinding attack model, where Eve probabilistically applies a blinding attack without being caught by using only an existing intuitive countermeasure. More precisely, our countermeasure solves the problem of how to define the bound in the limitation of precision of current detection, and then we prove security of the practical system by considering the current parameter. Meanwhile, we discuss the bound of the quantum bit error rate (QBER) introduced by Eve, by which Eve can acquire information without the countermeasure.
Introduced in 1984, quantum key distribution (QKD)[1, 2] allows two remote parties, the sender (Alice) and the receiver (Bob), to exchange secret keys. The unconditional security of QKD has been proved in theory for ideal systems.[3– 5] More generally, the security of the practical QKD system has been proved by considering some imperfections.[6– 8]
However, the equipment used in the practical systems has some loopholes, [9, 10] which can be exploited by Eve without being discovered or introducing only a small bit error rate. In fact, a series of quantum eavesdropping strategies have been discovered, [11] such as PNS attack, [12, 13] phase-remapping attack, [14, 15] time-shift attack, [16, 17] and wavelength-dependent attack.[18] Recently, several proposed attacks have focused on the measurement equipment, single-photon detectors, which are based on the concept of faked states attack.[10] Soon afterwards, a new concept, called measurement device-independent QKD (MDIQKD), [19, 20] was proposed to remove all detector side-channel attacks. However, it requires a Bell-state measurement of two independent remote laser sources, which is experimentally challenging to implement.[21, 22] For this reason, before the application of the MDIQKD system, it may be more practical to consider a valid countermeasure for the current large-scale QKD system. Furthermore, a countermeasure that is effective against a class of attacks has great significance in a practical QKD system. A typical example of an attack on single-photon detectors is a blinding attack, by which Eve can obtain a full copy of the raw key while causing zero additional quantum bit error rate (QBER).[23, 24] Some researchers proposed that monitoring of APD current can reveal Eve’ s blinding attack, as most of the published blinding attacks will lead to high photocurrent.[25] However, when limited to the precision of practical measurement equipment, if an attack only slightly increases the photocurrent, this intuitive countermeasure seems to fail to discover Eve’ s presence.
Inspired by this perspective, we propose a different attack model, called “ probabilistic blinding attack” . As the original blinding attack involves converting avalanche photodiodes (APDs) into linear mode, the blinding light generates an obvious photocurrent that can easily be detected. Therefore, if Eve partially blinds a single-photon detector with a certain probability, she can still obtain some information if the photocurrent caused by the attack is less than the detectable range. Meanwhile, within the limits of physical principles and the technological accuracy of existing equipment, the photocurrent fluctuation at Bob’ s single-photon detector under attack includes at least three parts: photocurrent fluctuation of the normal avalanche, photocurrent fluctuation caused by Eve and instrument noise. However, we attribute the fluctuation to Eve’ s attack when considering security. Note that fluctuation caused in physical principle results in a situation, that the “ probabilistic blinding attack” model cannot be completely avoided only by improvements in technology, but needs to be solved in theory. Hence, for all kinds of blinding attacks, we demonstrate a proof-of-principle countermeasure. Our countermeasure solves the problem of how to define the detectable bound with current equipment, and at the same time, under the detectable bound we provide a method of removing Eve’ s information and finally obtaining the secure key. Moreover, we discuss the range of QBER that Eve can increase in a successful blinding attack.
The rest of this paper is organized as follows. Section 2 describes the probabilistic blinding attack model. In Section 3, we elaborate a countermeasure against all kinds of blinding attacks, and we give a security analysis. In Section 4, we discuss the influence of the introduction of QBER by Eve. Finally, conclusions are drawn in Section 5.
In this section, we briefly review blinding attacks in a QKD system[24] and then propose a model, called the probabilistic blinding attack. Under the restrictions of precision in current equipment, the legitimate parties may fail to perceive this kind of attack.
The key device of a single-photon detector in most commercial QKD systems is the avalanche photodiode (APD). APD has two operation modes. When biased above the breakdown voltage, APD is in Geiger mode, and it can detect single photons. However, when its bias voltage is below the breakdown voltage, APDs are insensitive to single photons. During this period, the detectors only respond to classical light.
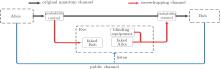
In practical telecom application, most single-photon detectors are operated in gated mode and are sensitive to single photons only when a photon arrives during the gate time window. In this situation, note that Eve can take measures called blinding attack, according to the following steps, to obtain information without being noticed. First, Eve can blind the gated single-photon detector using bright continuous-wave (c.w.) illumination, thus converting it to a classical, linear detector. Afterwards, the single-photon detector is no longer sensitive to single photons. In this case, assuming that Eve has sufficient ability to acquire a copy of the legitimate receiver’ s detection apparatus, then she can intercept Alice’ s signals, measure them, and resend bright trigger pulses instead of single photons based on the measurement results. Hence, Bob will detect the bit value sent by Eve if he uses the same basis as Eve, and otherwise, with incompatible bases, his detectors will remain silent. Next, Eve can sift the data according to the legitimate parties’ basis choices by eavesdropping on their public channel. Finally, Eve succeeds in obtaining full information on the raw key while causing zero QBER.[24] Although the intercept-to-resend process loses 50% of the bits, Eve can compensate for them by improving her transmittance. In addition to the method described above, there are other kinds of blinding approaches, such as CW thermal blinding, thermal blinding of frames, and sinkhole blinding.[26] Meanwhile, detectors that operated in other kinds of quenched modes have been reported to be vulnerable to such blinding attacks, [23, 27] which all lead to the same result: the APDs are forced to quit the single-photon sensitive Geiger mode and manipulate the detectors in the linear mode. The power of blinding light and the faked-state light is far higher than the normal signals. Therefore, some research groups put forward some countermeasure such as monitoring the photocurrent for anomalously high values.[28, 29] However, this intuitive viewpoint suffers from the issue that there is no security proof.
In the first phase, we present an improved model called the “ probabilistic blinding attack model” built on the foundation of the original blinding attack, so that the intuitive approach of monitoring photocurrent may fail to be effective. This theoretical model, aimed at APD singe-photon detectors in all operated modes, is applicative to the kinds of blinding attacks that have currently been reported.
Figure 1 displays the schematic composition of a probabilistic blinding attack. A probabilistic blinding attack is defined as an eavesdropper; Eve adopts a probabilistic blinding attack on the bits that Alice sent to Bob, that is, each time Eve intercepts information with a certain probability by the probability control block, then makes Bob blind, and resends faked states to Bob operated by the probability control block. After a series of operation in such a manner, the signals received by Bob have two parts: the classical laser light sent by Eve and the normal single-photon signals transmitted from Alice. Therefore, after Alice and Bob publicly announce basis choice, then they retain the identical basis choices, Eve will obtain part of the information. Despite previous literature showing that 100% blinding attack leads to an obvious increase in photocurrent, [29] note that Eve eavesdrops only on a small part, and due to the limited equipment accuracy resulting from restrictions of current technology, monitoring the photocurrent may fail to prevent QKD systems being attacked.
In order to prevent all kinds of blinding attacks, we propose a countermeasure that is easier to implement in large-scale applications. It can either use current equipment to achieve, or overcome the limited accuracy of current equipment that may be due to the escape of Eve. Here, we assume that all fluctuation comes from Eve’ s operation. Although this assumption might lose a few parts of keys, our measure improves the security of the QKD system. Moreover, under the detectable bound, we provide the method to remove Eve’ s information in the secure key, we also give its security analysis.
Owing to the limitations of current technology, we set the threshold value for the monitoring equipment according to the accuracy of the equipment. We use them to measure the current in Bob’ s single-photon detector. We define I0 is the current without being attacked, I1 is the current when the QKD system suffers the blinding attack, which means that the bits which are received at Bob’ s are all classical laser light sent by Eve. The difference between the two values is defined as Δ I. Then their relationship can be written as
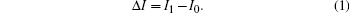
In a blinding attack, the difference can be clearly detected. By contrast, when Eve applies a probabilistic blinding attack, we assume that the percentage of the faked-state sent by Eve in all received bits at Bob’ s detector is α . The measurement accuracy of the monitoring current equipment is larger than p. Then we prove that the equipment can detect the probabilistic blinding attack if the practical current satisfies
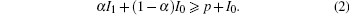
Then, the detectable minimum of the percentage of the faked-state sent by Eve in all received bits at Bob’ s could be written as
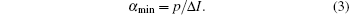
Therefore, our countermeasure can be established as follows. Within the range that the equipment can detect, this means that the percentage of the faked-state is larger than α min, we can become effectively aware of Eve’ s attack. While the percentage of the faked-state is less than α min, we can amend the scheme in privacy amplification to remove the part of eavesdropping and finally get the secure keys.
Huang[30] proposed the decoy state method, Gottesman et al.[6] gave the GLLP formula for the key generation rate as follows:
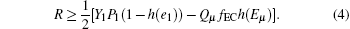
Here, 1/2 is the parameter for the BB84 protocol, Y1 is the single-photon state count rate, P1 is the sender’ s single-photon probability, e1 is bit error rate of single-photon state, μ denotes the average photon number of signal states, Qμ is the detector’ s response probability caused by signal states at Bob’ s side, fEC is the error correction inefficiency function, Eμ is the signal states bit error rate in QKD system, and h(x) is the binary Shannon information function, with the form

Note that only single-photon states can form the final key. In a probabilistic blinding attack, in order to obtain the lower bound of the secure keys, we should get the lower bound of Y1 and the upper bound of e1. When the percentage of faked states is less than α min, the original lower bound of Y1 should be corrected as (1 − α min)Y1. At the same time, e1 consists of two parts

In the case of a probabilistic blinding attack, e1sp is the bit error rate of a single-photon state attack, e1fs is the bit error rate of the faked-states sent by Eve. As e1fs ≥ 0, therefore, e1 should be correct as e1sp, and we can get the upper bound of e1sp as follows:
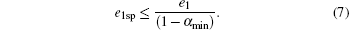
Combining all of the above, we conclude that the final secret key rate is

We give numerical simulation results based on the above analysis result. The parameters for the simulation reported in Ref. [31] are shown in Table 1.
| Table 1. List of parameters for numerical simulations. |
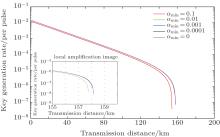
Figure 2 shows the relationship between key generation rates and the transmission distance with different α min. Thus, we can bound the threshold to prevent information leakage. Under the detectable bound, we provide the method to remove Eve’ s information in the secure key, and finally get the secure keys.
In this section, we discuss the range of QBER caused by Eve when Eve can eavesdrop on information. In a practical probabilistic blinding attack, Alice and Bob usually tolerate a nonzero QBER, so Eve might introduce a small QBER without being revealed. The detection probability for the faked state when Eve uses the matched basis is less than 1, which will lead to the loss, and the detection probability of half power of the faked state when Eve uses the mismatched basis is greater than 0, which will contribute to extra QBER. Although dark counts could also add to the error rate, however, we can assume that Eve can minimize the dark counts. Consequently, to simplify the analysis, we define the QBER as all coming from the eavesdropper, where dark counts have been omitted. Therefore, the QBER introduced by Eve in each attack is σ . In a probabilistic blinding attack, considering the probabilistic blinding parameter α defined in Section 3, the final QBER e can be given by

The security key rate formula BB84 protocol can be given by the formula of the entanglement purification protocol. The bit error is equal to the phase error, so the consumption of key correction is h2(e), and the consumption of privacy amplification is 1 − h2(e), [4] and then the secure key rate can be expressed as follows:
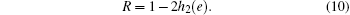
Let the above formula be zero, and we can obtain the critical error rate is 11%, which means that no secret key can be generated if e ≥ 11%. Suppose that the amount of raw key for legitimate communicating parties is R, and then the consumed key in post-processing is Rh2(e). The amount of raw key for Eve in a probabilistic blinding attack is
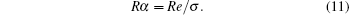
For Eve to obtain information, the amount of raw key for Eve in a probabilistic blinding attack should be more than the amount of raw key for the legitimate communicating parties
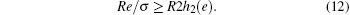
We can deduce the upper bound of σ to be
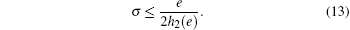
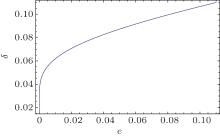
Figure 3 displays the relationship between the QBER introduced by Eve in each attack σ and the final QBER in the whole process e. The scope of e is not more than 11% because Alice and Bob usually tolerate typically less than 11%. The region below the solid curve means that Eve can obtain part of the information, as the amount of raw key for the legitimate parties is smaller than the amount of raw key for Eve in a probabilistic blinding attack. The tolerable range of QBER caused by Eve should be satisfied in the region, which is also a necessary condition for Eve to implement a successful probabilistic blinding attack in the absence of any countermeasure.
In summary, we propose a probabilistic blinding attack model in this work. It is a general attack model for APDs singe-photon detectors and suitable for all operation modes, which can help Eve to avoid the photocurrent detection compared with the original blinding attack model. Moreover, we consider all the fluctuation of photocurrent due to Eve’ s attack in order to improve the security of QKD. We then give a countermeasure against all kinds of blinding attacks, along with a precise security analysis to remove Eve’ s information in the secure key. Finally, we discuss the upper bound value of QBER caused by Eve to obtain the secret key information in a blinding attack. Given the detectable photocurrent parameter, we can employ the post processing to avoid this attack, thus it can be directly applied in the practical QKD systems.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|