†Corresponding author. E-mail: mffang@hunnu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11374096 and 11074072).
We investigate the quantum-memory-assisted entropic uncertainty for an entangled two-qubit system in a local quantum noise channel with
Conventional quantum mechanics requires the Hermiticity of the Hamiltonian of a physical system to ensure that the energy of the system is real and that the time evolution is unitary. In 1998, Bender et al. proposed a class of Hamiltonian, the so called parity– time (
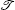

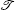
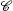
The 
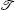

where s is a general scaling constant of the matrix, angle α ∈ (− π /2, π /2) characterizes the non-Hermiticity of the Hamiltonian, and s and α are real numbers. If α = 0, then H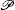


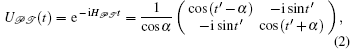
where t′ = Δ Et/2, Δ E = E+ − E− , and E± = ± scosα are the eigenvalues of H
On the other hand, as one of the fundamental ideas of quantum theory, the uncertainty principle reveals that the characteristics of quantum mechanics distinctively differ from those of the classical world. The principle constrains the uncertainty about the outcomes of two incompatible measurements performed on a particle. A good way to understand the uncertainty principle is through the uncertainty game between two players, Alice and Bob. They begin the game by agreeing on two measurements Q and R. Bob then prepares a particle A and sends it to Alice. Alice performs one of the two measurements randomly on the particle A and announces her choice but not the outcomes to Bob. The question is whether Bob can predict Alice' s measurement outcomes, this uncertainty can be quantified by the entropic uncertainty relation[12– 14]
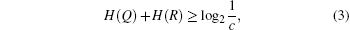
where H(X) denotes the Shannon entropy of the probability distribution of the measurement outcomes of observable X, which can be diagonalized by eigenstates 
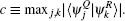
However, when the particle A is initially prepared in an entangled state with another particle B, then the particle B can provide quantum information as an aid to minimize the uncertainty about all of the possible measurements on the particle A, and hence Bob can beat the bound. The particle B can be seen as a quantum memory. If A and B are maximally entangled, then the uncertainty of the two measurements vanishes and Bob can guess both Q and R perfectly. The improved entropic uncertainty relation depending on the amount of entanglement is[15]

where S(A| B) is the conditional von Neumann entropy.[16]S(X| B) is the conditional von Neumann entropy of the post-measurement state. Mathematically, a lower bound could be obtained in Eq. (4) by a negative conditional entropy S(A| B) for the entangled system. Equation (4) is named the quantum-memory-assisted entropic uncertainty relation and it has been experimentally proven by Berta et al.[17, 18]
In effective quantum information processing, however, quantum systems are inevitably exposed to environmental noise.[19] One of the consequences of the interaction between the system and its environment is decoherence, which can be viewed as the loss of information of the system and thus system' s entropic uncertainty increases.[20, 21] As far as we know, few operations have been discovered to reduce the entropic uncertainty of a quantum system. In this paper, we investigate the behavior of quantum-memory-assisted entropic uncertainty in an entangled qubits system under local 


We consider the uncertainty game for a two-qubit system. Initially, Bob prepares a pair of qubits in the maximally entangled state

and then sends qubit A to Alice. For quantum information processing, qubit A suffers from an amplitude damping noise channel identified by damping rate r, while qubit B is free from environmental noise as a quantum memory kept by Bob. The amplitude damping channel can be described by operation elements as[16]
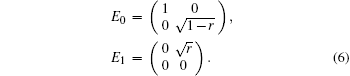
The state of the qubits system after passing through the local amplitude damping channel can be given in sum-operator representation as
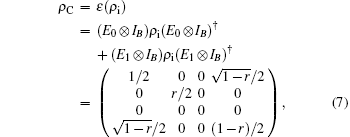
where IB is the identity operator of qubit B (similarly hereinafter), and ρ i = | Ψ i⟩ ⟨ Ψ i| .
After qubit A experiences the noise channel, we immediately perform a local 
The evolved state of the system can be obtained by using the time-evolution operator introduced in Eq. (2). Then, the final state of the system is
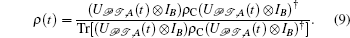
To evaluate the quantum-memory-assisted entropic uncertainty, we employ the Pauli operators for measurements. Without loss of generality, let Q = σ x and R = σ z. After qubit A has been measured, the post-measurement state of the system will be
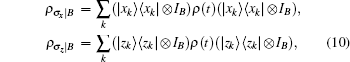
where {| xk⟩ } ({| zk⟩ }) are the eigenstates of the observable σ x (σ z).
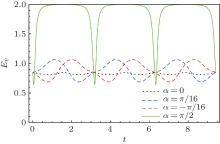
We use EU to represent the quantum-memory-assisted entropic uncertainty in the system. The dynamics of EU under the local 


To further illustrate the efficiency of the local 

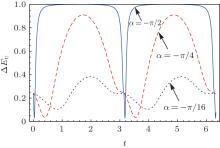
Another task is to reduce EU to its lower bound. We use EU, b to represent the lower bound of EU. The EU reaches its lower bound EU, b for the maximally entangled state Ψ i given by Eq. (5). However, after being subjected to the amplitude damping channel, EU is greater than EU, b. By performing the local 
We give possible physical explanations for the above behavior of EU based on the property of entanglement of the qubits system and the Non-Hermiticity of the 
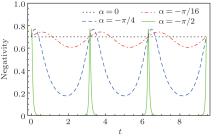
As one of the most important resources in quantum information and quantum computation, quantum entanglement[22– 24] has attracted much attention in recent years.[25– 29] The increase of entanglement can be employed to account for the reduction of EU according to the conception of the quantum-memory-assisted entropic uncertainty relation. We use negativity to measure the degree of entanglement[30]

which is equal to the absolute value of the sum of negative eigenvalues of ρ (t)T. Here ρ (t)T is the partial transposition of ρ (t). Figure 5 gives N against t when a local 


Another more essential explanation for the reduction of the entropic uncertainty in the qubits system by the local 
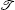

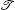
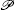
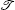

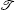
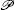


with
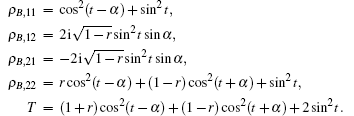
This means that the local non-Hermitian 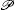
We have investigated the reduction of the entropic uncertainty in an entangled qubits system via the amplitude damping channel by a local 
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|