†Corresponding author. E-mail: hszeng@hunnu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11275064 and 11075050), the Specialized Research Fund for the Doctoral Program of Higher Education, China (Grant No. 20124306110003), the Scientific Research Foundation of the Education Department of Hunan Province, China (Grant No. 13C039), and the Construct Program of the National Key Discipline, China.
We study the effects of the interaction strength and the initial phase on the dynamics of quantum discord in a two-qubit system under both spontaneous emission and dephasing noisy channels. It is shown that the time evolution of quantum discord displays quicker oscillations with increasing inter-qubit interaction strength but the effect of the initial phase closely depends on the interaction between the qubits. Only for non-zero inter-qubit interaction cases, the evolution of quantum discord is affected by the initial phase and its oscillating amplitude increases with increasing initial phase. A comparison between evolutions of quantum discord and entanglement is also made.
Quantum correlation, as a distinctive characteristic of the quantum world that distinguishes it from its classical counterpart, has aroused the curiosity of scientists.[1] As forms of the description of quantum correlation, quantum entanglement (QE)[2] and quantum discord (QD)[3] have been successively proposed and they have attracted extensive research.[4– 6] QD is usually regarded as the measure of all nonclassical correlations in a bipartite system, which includes QE as a particular case. It has been shown that separable states with nonzero QD can be used to perform quantum computation.[7, 8] However, the evaluation of QD is in general more sophisticated than QE and analytical expressions are known only for certain classes of states.[9– 15]
A quantum system inevitably interacts with its environment, leading to the change of the quantum correlation. Over the past decade, the influence of the environment on QE[16– 18] and QD[19– 24] has been extensively investigated. A well-known phenomenon, the so-called entanglement sudden death (ESD), [25] in an entangled two-qubit system exposed to local Markovian environments has been discovered and demonstrated experimentally.[26] By contrast, QD in similar conditions only decays in asymptotic ways, [27] which means that QD is more robust against Markovian noises than QE. Even in non-Markovian environments, QD seems to preserve this superiority.[28]
In the previous study of the evolution of quantum correlation in open quantum systems, most works have mainly concentrated on those cases in which the multi-body system is in a correlated initial state and there is no interaction between the components.[29– 34] Although some works[35– 37] have also investigated coupled open quantum systems, there are still some problems that need more discussion and further study. In this paper, we study the QD dynamics of a pair of coupled qubits that are initially in a specific entangled state and influenced by spontaneous emission or dephasing noises. We find that QD displays faster oscillations with increasing inter-qubit interaction strength. Furthermore, when the interaction is absent, the evolution of QD is independent of the initial phase of the state. With non-zero interactions, the oscillation amplitude of QD increases with the initial phase. We compare the evolutions between QD and QE in the considered noisy channels.
The rest of this paper is arranged as follows. In Section 2, we introduce the definition of QD and present a method to calculate both QD and QE for the X state. In Section 3, we present the analytical expressions for the dynamical evolution of the coupled qubit system under the influence of spontaneous emission and dephasing noises, respectively. In Section 4, we numerically discuss the dynamical features of QD and QE. Finally, we give a summary of our results in Section 5.
Quantum discord, which was initially introduced by Ollivier and Zurek, [3] is defined as the difference between total and classical correlations

Here the total correlation of a bipartite quantum state ρ is measured by quantum mutual information I(ρ ) = S(ρ A) + S(ρ B) − S(ρ ), where S(ρ ) = − Tr(ρ log2ρ ) is the von Neumann entropy, and ρ A(B) = TrB(A)(ρ ) are the reduced density operators for subsystems A (B). The classical correlation may be expressed as C(ρ ) = S(ρ A) − min{Π k}S(ρ | {Π k}), where we have assumed that an orthogonal projector measurement {Π k} is performed on sub-system B, with pk = Tr(I ⊗ Π k)ρ (I ⊗ Π k) being the probability of outcome k, and ρ k = 1/pk(I ⊗ Π k)ρ (I ⊗ Π k) and S(ρ | {Π k}) = Σ kpkS(ρ k) are the corresponding conditional density matrix and conditional entropy. The minimum is across all possible orthogonal projector measurements. Clearly, QD may be equivalently expressed as
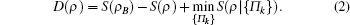
In this paper, we are mainly interested in the dynamics of two-qubit X states. For this class of states, QD may be calculated analytically. Consider a two-qubit X state with density operator
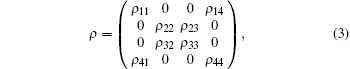
which has eigenvalues
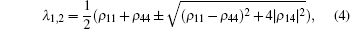
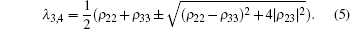
The mutual information can be expressed as
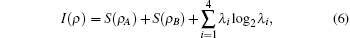
with
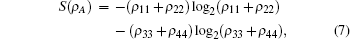
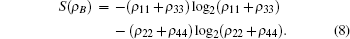
The calculation of the classical correlation is a bit complex due to the minimization of the conditional entropy but is possible in principal. Using the method in Refs. [28] and [38], we finally obtain the analytical expression of QD for the above X state
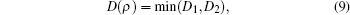
where 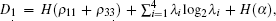
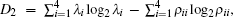
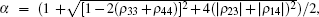
Besides QD, we also investigate the evolution of QE and compare it with the dynamics of QD. We use Wootter’ s concurrence as the measure of QE.[39, 40] For the X state given above, the concurrence may be expressed as
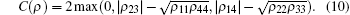
In the model discussed below, due to ρ 14 = 0, the concurrence reduces further to

Different environments can cause different decoherence effects for a given open quantum system. In this section, we consider a system that consists of two identical coupled qubits A and B, which has Hamiltonian (setting ħ = 1),

where v is the interaction strength between the two qubits, and 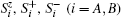
First, we consider the case in which the two qubits encounter independently spontaneous emission noises. The dynamics of the system are governed by the quantum master equation
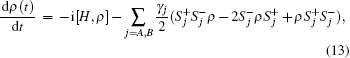
where ρ (t) is the reduced density operator of the two qubits, and γ A and γ B are the spontaneous decay rates of qubits A and B, respectively. In order to investigate the dynamics of QD, we assume a class of initial states ρ (0) = 1/3(a| ee⟩ ⟨ ee| + d| gg⟩ ⟨ gg| + | ψ ⟩ ⟨ ψ | ), where | ψ ⟩ = | eg⟩ + z| ge⟩ and a ≥ 0, d = 1 − a, z = eiχ . This state has the structure of the Werner state, [41] and the real parameter χ is the initial phase to be concerned. In the qubit standard product basis {| ee⟩ , | eg⟩ , | ge⟩ , | gg⟩ }, the initial state has the form of X state,
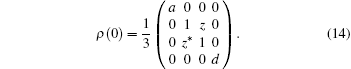
We can prove from the quantum master equation (13) that the dynamical evolution of this initial state preserves the X-state form.[37] For the sake of simplicity, we assume equal decay rates γ A = γ B = γ for the two qubits. After some tedious calculations, we obtain the reduced density matrix of the qubit system at time t

with the nonzero density matrix elements given by
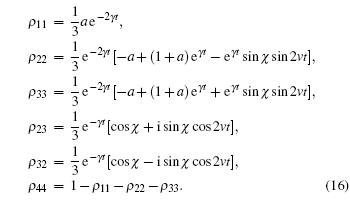
With these results, the quantum correlations given by Eqs. (9) and (11) can be calculated directly, either analytically or numerically.
Next, we consider the well-known model of the so-called pure dephasing noise, i.e., the coupled two qubits encounter independent dephasing noises. The master equation that governed the evolution of the reduced system reads
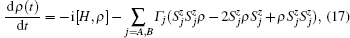
where 2Γ A(B) is the dephasing rate of qubit A (B). For simplicity, we assume Γ A = Γ B = Γ and v > 2Γ . Under the same initial condition of Eq. (14), the dynamical state of the reduced system at any time still has the form of Eq. (15). The nonzero matrix elements can now be written as
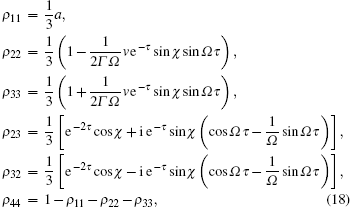
with 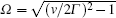
In this section, we investigate the evolutional features of quantum correlation of the coupled qubit system in the noisy channels. First, we consider the case with spontaneous emission noise. In Fig. 1, we plot QD as a function of the rescaled time γ t for the system with different inter-qubit interaction strength v, where the qubits are initially in the entangled state given by Eq. (14) with a = 0.4 and χ = π /2. It can be seen that when the interaction strength v = 0, i.e., the two qubits in the system are not coupled, QD exhibits a monotonic decay with time. For non-zero inter-qubit interactions (say v = 5γ , 10γ in the figure), QD displays damped oscillations. The larger that the interaction strength is, the quicker the QD oscillates. Interestingly, all of the oscillation curves have the same envelope, which is given by the damping line with v = 0. Physically, the oscillations arise from the inter-qubit interaction and the damping envelope is due to the spontaneous emission.
 | Fig. 1. Time evolution of QD under spontaneous emission noise for different interacting strengths: v = 0, v = 5γ , and v = 10γ . The initial state is given by Eq. (14) with a = 0.4 and χ = π /2. |
In Fig. 2, we show the QD as a function of the rescaled time γ t for the given X state with different initial phase χ , where we set a = 0.4 and v = 5γ . The initial phase is chosen to be χ = π /6, π /4, and π /2, respectively. It can be seen that the dynamics of QD depends closely on the initial phase χ . The larger the initial phase, the larger the amplitude of the QD oscillation. These oscillation curves also have a common envelope which is still given by the monotonic decay line with v = 0 (not shown in the figure). It is worth pointing out that the phase dependence of QD exists only for nonzero inter-qubit interaction cases. If the interaction vanishes, then the dependency of QD on phase χ would also disappear, which may be verified directly by putting Eq. (16) into Eq. (9). Because of the complexity of the expression, we do not present it here. The phenomenon that the relation between QD and the initial phase is modulated by the inter-qubit interaction is one of main results in this paper.
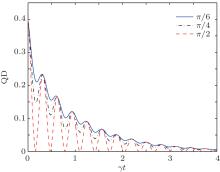 | Fig. 2. Time evolution of QD under spontaneous emission noise for different initial phases: χ = π /6, χ = π /4, and χ = π /2. The initial state is given by Eq. (14) with a = 0.4, and the inter-qubit interaction strength is v = 5γ . |
To compare the QD and QE dynamics, we show the time evolutions of QD and concurrence in the same figure (Fig. 3), where we set a = 0.4, χ = π /2, and v = 5γ . It is shown that the evolutional forms of QD and concurrence are basically the same, while the oscillation of QD sustains longer, indicating that QD is more robust than entanglement in the spontaneous emission noise. The robustness of QD was previously shown.[27, 42]
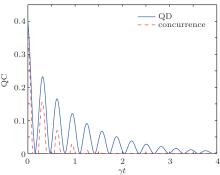 | Fig. 3. Quantum correlation as a function of rescaled time γ t for the qubit system under the spontaneous emission noise. Here a = 0.4, χ = π /2, and v = 5γ . |
Next, we address the evolution of QD in the considered system under dephasing noise. In Fig. 4, we plot the time evolution of QD for the given X-state with a = 0.4, χ = π /2, and different interaction strengths. It is not difficult to find that the evolution of QD is similar to that under spontaneous emission noise (see Fig. 1), i.e., QD decays monotonically in the zero interaction case and oscillates more quickly with the increase of the interaction strength. The difference is that here QD exhibits a sudden change for the zero interaction and the oscillation curves for non-zero interactions have no common envelope. In Fig. 5, we show the time evolution of QD for different initial phases under dephasing noise. It also exhibits a similar behavior as that under the spontaneous emission noise (see Fig. 2); i.e., the oscillation amplitude of QD increases with the phase χ when the inter-qubit interaction is non-zero. Similarly, the oscillation curves have no common envelope. We can also directly verify with Eqs. (9) and (18) that the effect of the initial phase on the evolution of QD exists only in the non-zero interaction cases. In the zero inter-qubit interaction case, QD does not depend on the initial phase. Finally, we compare the evolutions of QD and concurrence in this dephasing model, as shown in Fig. 6. The similarity in the evolution of QD and concurrence, and the robustness of QD are apparent.
 | Fig. 4. Time evolution of QD under dephasing noise for different interacting strengths: v = 0, v = 5Γ , and v = 10Γ . Here a = 0.4 and χ = π /2. |
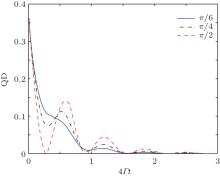 | Fig. 5. Time evolution of QD under dephasing noise for different initial phases: χ = π /6, χ = π /4, and χ = π /2. Here a = 0.4 and v = 10Γ . |
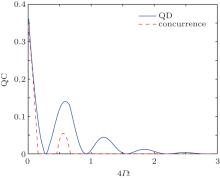 | Fig. 6. Quantum correlation as a function of rescaled time 4Γ t for the qubit system under dephasing noise with a = 0.4, χ = π /2, and v = 10Γ . |
Note that the dynamics of concurrence for two coupled qubits under the influence of spontaneous emission and dephasing noises was studied.[37] Comparing our results of QD with theirs for QE, we find that the evolutions of the two kinds of quantum correlations have some similar features, such as the similar dependence of QD and QE on the inter-qubit interaction. This of course does not mean the triviality of our work, because QD and QE are essentially two different quantities. In fact, we have also found some new results; for example, the inter-qubit interaction can modulate the effect of the initial phase on the QD dynamics.
We have investigated the QD dynamics of two coupled qubits embedded, respectively, in spontaneous emission and dephasing noisy channels. We have found that, in general, the QD evolution depends not only on the inter-qubit interaction but also on the phase of the initial entangled state. QD displays quicker oscillations with increasing interaction strength under either spontaneous emission noise or dephasing noise. The effect of the initial phase is modulated by the inter-qubit interaction strength. When the interaction is absent, the dynamics of QD are independent of the initial phase. For non-zero inter-qubit interaction cases, the evolution of QD depends closely on the initial phase. The larger the initial phase, the larger the amplitude of the QD oscillation. Distinctively, in the case of spontaneous emission noise, the damping oscillations of QD for different inter-qubit interactions or initial phases have a common envelope, while for the case of dephasing noise this property disappears. We have also compared the evolutions of QD and QE, and have found that they display some similar behaviors and QD is more robust than QE in both kinds of noisy channels.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|


