Quantum phase transitions (QPTs) are driven purely by the quantum fluctuations when a parameter of the Hamiltonian describing the system varies.^{[1– 3]} Traditionally, QPTs can be well understood in the framework of the Landau– Ginzburg– Wilson paradigm by resorting to the notions of local-order parameter, long-range correlations and the symmetry breaking. In the past few years, a lot of efforts have been devoted into understanding the QPTs from the information-geometry perspectives, ^{[4, 5]} such as quantum entanglement, ^{[6– 9]} entanglement entropy, ^{[10, 11]} quantum discord, ^{[12– 14]} quantum fidelity and fidelity susceptibility, ^{[15– 21]} Berry phase^{[22– 32]} and the quantum geometric tensor (QGT).^{[33– 41]}

Generally, QPTs can be witnessed by some qualitative changes of the ground-state properties when some parameters of the Hamiltonian move across the quantum critical point (QCP). The underlying physical mechanism lies in the fact that the different phases are unconnected by the adiabatic evolution of the ground state. In the vicinity of the QCP, the ground state driven by the parameters of the Hamiltonian will lead to an avoided energy-level crossing between the ground state and the first excited state, where the adiabatic evolution can be destroyed by a vanishing energy gap as the system size tends to infinity. From the perspective of the information geometry, a monopole as a gapless point in the Hamiltonian parameters space will generate interesting effects on the ground-state local or topological properties. The local properties can be captured by some local quantities, i.e., the fidelity susceptibility and the Berry curvature. The topological properties will be captured by some topological quantum numbers, i.e., the Chern number, ^{[42, 43]}Z₂ number, ^{[44– 47]} and recently the Euler number of the Bloch states manifold.^{[48– 51]}

Recently, the concept of quantum geometric tensor based on the information-geometry^{[52, 53]} of the ground state has been introduced to understand the QPTs in quantum many-body systems.^{[37– 41]} What is surprising is that the two approaches of the ground-state Berry curvature and the fidelity susceptibility as some witness to QPTs are unified. Specifically, the real part of the QGT is a Riemannian metric defined in the parameter manifold which has been recognized as the essential part of the fidelity susceptibility. Meanwhile its imaginary part is the Berry curvature whose flux gives rise to the Berry phase. Generally speaking, the Riemannian metric and the Berry curvature will exhibit some singularity or scaling behavior in the quantum critical region under the thermodynamic limit. Particularly, a scaling analysis of the ground-state quantum geometric tensor in the vicinity of the critical points has been performed. So far, these approaches have been applied to detect the phase boundaries in various systems.

In this work, we propose a cyclic quantum distance of the ground state to detect the QPTs in a transverse field inhomogeneous Ising spin-1/2 chain, ^{[54, 55]} in which the nearest-neighbor exchange interactions will take alternating parameters between the neighbor sites. This model can be solved exactly by introducing a general canonical transformation to diagonalize the fermionic Hamiltonian mapped from the spin Hamiltonian by the Jordan– Wigner transformation. In our scheme, an extra local gauge transformation is performed to the spin system by a twist operator, which endows the Hamiltonian of the system with a topology of a ring S¹ without changing its energy spectrum. We obtain the exact expression of the ground-state Riemannian metric and study the cyclic quantum distance of the ground state on the parameter manifold. We study extensively the ground-state Riemannian metric in different parameter regions of the inhomogeneous Ising chain. Particularly, we show that the quantum ferromagnetic phase in the uniform Ising chain can be marked by an invariant cyclic quantum distance of the ground state, and meanwhile, this distance will decay to zero rapidly in the paramagnetic phase.

Let us consider an inhomogeneous two-sublattice Ising spin-1/2 chain in an external magnetic field, which consists of N cells with two sites in each cell. The Hamiltonian reads

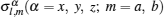
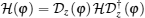
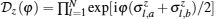
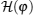
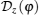
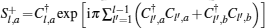
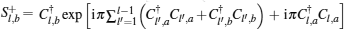
where are the local Pauli operators, J_a (J_b) is the exchange coupling, h is the external field and the periodic boundary condition (PBC) has been assumed. In order to investigate the model in a two-dimensional quasi-momentum space, we put this model on an external parameter φ -ring S¹. This can be achieved by subjecting the system to a local gauge transformation by a twist operator , which in fact makes the system rotate on the spin along the z direction. It can be verified that is π periodic in the parameter φ . Considering the unitarity of the twist operator , the energy spectrum and critical behavior of the system are obviously independent with the parameter φ . The spin Hamiltonian can be mapped exactly on a spinless fermion model through the Jordan– Wigner transformation, i.e., and , where are the spin ladder operators, and C_{l, a(b)} are the fermion operators. Hamiltonian is transformed into

Note that the PBC on the spin degrees of freedom implies that C_{N+ 1, m} = e^{iπ N_F}C_{1, m}, where denotes the total fermion number. Thus the boundary conditions on the fermionic system will obey PBC or anti-PBC depending on whether N_F is even or odd. However, the differences between the two boundary conditions are negligible in the thermodynamic limit. Without loss of generality, we take the PBC on the fermionic system, which means C_{N+ 1, m} = C_{1, m}. Apply the following Fourier transformation and to the Hamiltonian H(φ ), where k = (2π /2aN)n, (n = 0, 1, 2, … , N − 1 and R_la (R_lb = R_la + a) is the coordinate of site a (b) in the l-th cell with the lattice parameter 2a. We can rewrite Hamiltonian in the quasi-momentum space

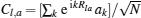
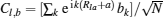
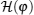
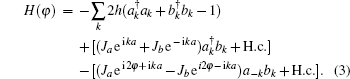
This Hamiltonian H(φ ) can be exactly diagonalized as

by using the following canonical transformation:

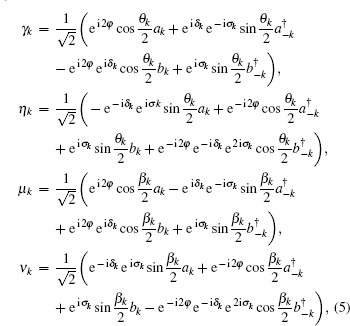
where

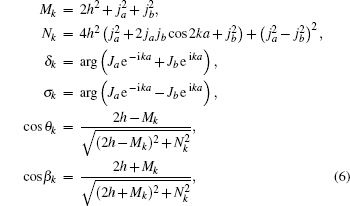
and the quasi-particle energy spectrums are

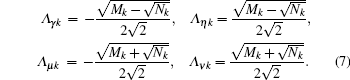
Now, we focus on the geometric properties of the ground state. The Hamiltonian H(φ ) in Eq.  (4) has been diagonalized in the set of quasi-particle number operators, which allows us to determine all the eigenvalues and eigenvectors. We note that the energy spectrums Λ _{η k} ≥ 0, Λ _{ν k} ≥ 0 and Λ _{γ k} ≤ 0, Λ _{μ k} ≤ 0. The ground state, denoted as | g(φ )〉 , corresponds to the state with the lowest energy, which consists of a state with no η and ν fermions occupied but with γ and μ fermions occupied. Explicitly, the ground state can be constructed as follows:

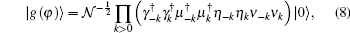
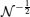
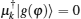
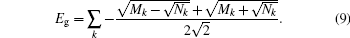
where is the normalized factor, and | 0〉 is the vacuum states of fermionic operators a_k and b_k, respectively. It is easy to check that η _k| g(φ )〉 = 0, ν _k| g(φ )〉 = 0 and , for all k. The corresponding ground-state energy E_g is

Now, we introduce the notion of the quantum geometric tensor of the ground state on the Hamiltonian parameter φ manifold. It can be verified that the quantum geometric tensor can be derived from a gauge invariant distance between two ground states on the U(1) line bundle induced by the quantum adiabatic evolution of the ground state in the parameter φ space. The quantum distance dS between two ground states | g(φ )〉 and | g(φ + δ φ )〉 is given by dS² = 〈 ∂ _φ g(φ )dφ | ∂ _φ g(φ )dφ 〉 . 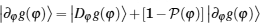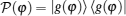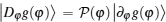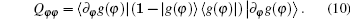Note that the term | ∂ _φ g(φ )〉 can be decomposed as , where is the projection operator and is the covariant derivative of | g(φ )〉 on the U(1) line bundle. Under the condition of the quantum adiabatic evolution, the evolution from | g(φ )〉 to | g(φ + δ φ )〉 will undergo a parallel transport in the sense of Levi– Cività from φ to φ + δ φ on the parameter manifold, and hence we can get | D_φ g(φ )〉 = 0. Finally, we can obtain the quantum distance as dS² = Q_{φ φ} dφ ², where Q_{φ φ} is defined as the quantum geometric tensor

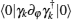
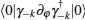
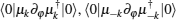
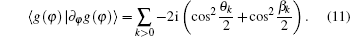
The concrete expression of Q_{φ φ} can be derived by substituting Eq.  (8) into Eq.  (10). Obviously, the straightforward calculation is tedious, however, it can be derived concisely from the following consideration. Notice that the term 〈 g(φ )| ∂ _φ g(φ )〉 is nothing but the Berry– Simon connection of the ground state, which can be calculated by considering that each term as and will yield the same result as − 2i cos²(θ _k/2), and will yield the result as − 2i cos²(β _k/2), and meanwhile, all the other terms are zero. Finally, we can get

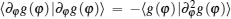
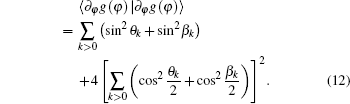
In order to calculate the term of 〈 ∂ _φ g(φ )| ∂ _φ g(φ )〉 , we note that because ∂ _φ 〈 g(φ )| ∂ _φ g(φ ) 〉 = 0 (see Eq.  (11)), and so we have

Substituting Eqs.  (11) and (12) into Eq.  (10), we can finally obtain the result as

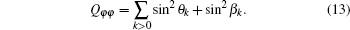
Now, let us focus on the characterization of the geometric properties for the ground state. In our approach, the ground state | g(φ )〉 is defined in a U(1) line bundle located over a one-dimensional parameter manifold S¹, and hence the Riemannian metric as the real part of the QGT is just Q_{φ φ} itself. As discussed above, the ground-state Riemannian metric provide a gauge invariant distance measurement of the ground state on the parameter φ manifold. The quantum distance l between two ground states | g(φ A)〉 and | g(φ B)〉 is given by

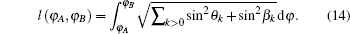
To have an explicit view of the dependence of the Riemannian metric on the system size, we can perform a scaling transform to the Q_{φ φ} and denote the Riemannian metric as 𝒢 _{φ φ} = Q_{φ φ} /L^d = [∑ _{k> 0} (sin²θ _k + sin²β _k)]/N, where L^d = N as the number of the site and here d = 1 is the dimension of the system. To study the quantum criticality, we are interested in the properties under the thermodynamic limit as N → ∞ , and we have the Riemannian metric

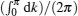
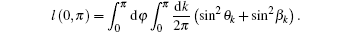
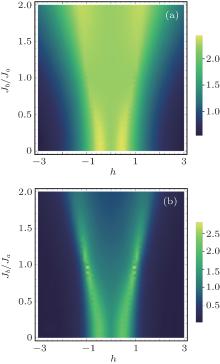
where the summation (∑ _{k> 0)/N} has been replaced by the integral . Obviously, the quantum distance l(0, π ) for a cyclical evolution from | g(0)〉 to | g(π )〉 is given by

In Fig.  1(a), we plot the cyclic quantum distance l(0, π ) as a function of h and α = J_b/J_a with the system size N → ∞ . As a comparison, we also provide numerical results of the second derivative of the ground-state energy with respect to h, as a function of J_b/J_a and h with the system size N = 1001 (see Fig.  1(b)). The cyclic quantum distance l(0, π ) as a function of the external field h with the fixed parameters J_a = 1 and J_b = 1.5 is shown in Fig.  2. In the region of the inhomogeneous coupling J_a ≠ J_b, the cyclic quantum distance and the Riemannian metric have similar trends with the second derivative of the ground-state energy.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) The cyclical quantum distance l(0, π ) as a function of Jb/Ja and h with the fixed parameter Ja = 1, and the system size N → ∞ ; (b) the second derivative of the ground-state energy Eg/N with respect to h, as a function of Jb/Ja and h with the fixed parameter Ja = 1, and the system size N = 1001.

Fig.  2.

	Figure Option ViewDownloadNew Window
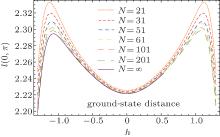	Fig.  2. The cyclical quantum distance l(0, π ) as a function h with the fixed parameters Ja = 1 and Jb = 1.5, and with different system sizes.

It is worth reminding that, in the uniform exchange coupling case J_a = J_b = 1 and the system size N → ∞ , the ground-state Riemannian metric 𝒢 _{φ φ} can be exactly solved as

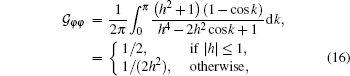
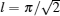
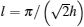
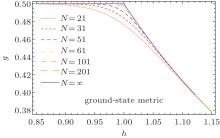which leads to an invariant ground-state cyclical distance in the ferromagnetic phase, and in the paramagnetic phase. In Fig.  3, we show the properties of the Riemannian metric in the vicinity of the critical points with fixed parameters J_a = J_b = 1 and different system sizes N. As shown in Fig.  3, the Riemannian metric of the ground state in the ferromagnetic phase is in close to the constant 0.5 with the increase of the system size N. In the thermodynamic limit N → ∞ , the first derivative of the cyclic distance and the metric are discontinuous in the critical point.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. The Riemannian metric g as a function of h with the fixed parameters Ja = Ja = 1, and with different system sizes.

For a measurable consequence of the Riemannian metric, it has been recently shown that the quantum geometric tensor of the Bloch bands can be measured by the current noise spectrum of the band insulators. The current noise spectrum can be expressed as (Eq.  (13) in Ref.  [40])

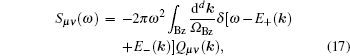
where Ω _BZ denotes the volume of the Brillouin zone and d denotes the dimension of the quasi-momentum space. The current noise spectrum is just defined as the Fourier transform of the current– current correlation function

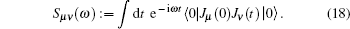
On the other hand, Marzari and Vanderbilt^[49] have pointed out that the integral of the trace of the Riemannian metric over the Brillouin zone can be regarded as a gauge invariant measure

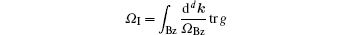
of the delocalization or spread of the Wannier functions.

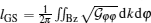
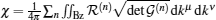
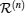
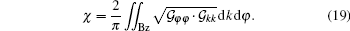
It is worth noting that the metric component Q_{φ φ} of the Bloch band is closely related to the ground-state quantum distance in the parameter φ space. In fact, the ground state | g(φ )〉 is π periodic in the parameter φ . In the condition of the large sites limit N → ∞ , a cyclic ground-state distance l_GS along the φ -ring can be calculated as , which only relates to the metric 𝒢 _{φ φ} on the Bloch band and the concrete expression of the ground state is not required. On the other hand, the topological Euler number index χ of the Bloch band is (see Ref.  [48]) given by , where is the Ricci scalar curvature associate to the Bloch state | u_n(k)〉 of the n-th Bloch band. In the present model, the expression of Euler number χ can be simplified as

The relation between the cyclic ground-state distance l_GS and the Euler number χ of the Bloch band illustrates that the cyclic ground-state distance is an intrinsic property of the Bloch bands. Meanwhile, this relation also tells us that the cyclic ground-state distance l_GS in the ferromagnetic phase of a uniform Ising chain is equivalent to the topological Euler number of the band in the quasi-momentum space.

In summary, we study the ground-state geometric properties of a two-sublattice quantum Ising chain in a transverse field. In particular, we introduce a gauge transformation to the spin system by a twist operator, which endows the Hamiltonian of the system with a topology of a ring S¹ without changing its energy spectrum. 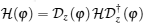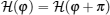The advantages of introducing the twist parameter is that the Hamiltonian describing the system is periodic of the parameter φ , i.e., . Hence, we can naturally discuss the Berry phase and the cyclic quantum distance on the φ -ring S¹. On the other hand, our approach can be easily extended to two dimensions because the fermionized system has a natural S¹ topology (the periodic gauge | u_n (k)〉 = e^{iG· r} | u_n(k + G)〉 , G denotes the reciprocal lattice vector) on the first Brillouin zone. Finally, the spin Hamiltonian can be naturally regarded as a fermionic Hamiltonian on a 2-torus T² = S¹ × S¹ in the parameter space (k, φ ). However, it is hard to find a natural S¹ or T² topological structure for the Hamiltonian if we take the Hamiltonian parameters J_a, J_b or h as the parameters manifold. Note that a nontrivial topological number for the quantum states requires a nontrivial topological structure of the Hamiltonian. This is the reason why we introduce a twist parameter to the Hamiltonian instead of using the Hamiltonian parameters J_a, J_b and h as the parameter manifold.

On the φ parameter manifold S¹, we derive the exact expression of the ground-state Riemannian metric and define a cyclic quantum distance of the ground state. We study extensively the ground-state Riemannian metric and the cyclic quantum distance in different parameter regions of the two-sublattice Ising chain. Furthermore, we show that the ferromagnetic phase of a uniform Ising chain can be characterized by an invariant quantum metric G_{φ φ} = 1/2 and this metric will decay to zero with h^{− 2} in the paramagnetic phase. While the metric G_{φ φ} is continuous in the critical point, the singularity will appear when we take the derivative of G_{φ φ} with respect to the external field h. This approach provides an intrinsic description of the geometric properties of the ground state. We hope that the current work will raise renewed interest in the understanding of the geometric nature of the ground state in quantum condensed-matter systems.