†Corresponding author. E-mail: bywang@njupt.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 61271232 and 61372126) and the University Postgraduate Research and Innovation Project in Jiangsu Province, China (Grant No. CXZZ12-0472).
Security against eavesdroppers is a critical issue in cognitive radio networks (CRNs). In this paper, a scenario consisting of one primary pair and multiple secondary pairs is considered. The secondary transmitters (STs) work in half-duplex mode and they are potential eavesdroppers on the primary transmission unless they are allowed to simultaneously transmit with the primary transmitter (PT). A modified second-price sealed-bid auction scheme is employed to model the interaction between the PT and STs. With the proposed auction scheme, the hostile relationship between the PT and STs is transformed into a cooperative relationship. An iterative algorithm based on the max–min criteria is proposed to find the optimal bidding power of the STs for an access chance in the presence of multiple eavesdroppers. Numerical results show that the proposed auction scheme not only improves the PT’s security but also increases the access opportunities of the STs.
Currently, demand for the wireless spectrum is increasing thanks to the rapid development of wireless communication. The cognitive radio network (CRN)[1] is a promising technique to solve this problem because it allows unlicensed users to coexist with licensed users.[2] However, it also introduces more security issues, which have attracted considerable attention.
Game theory is not only a proper mathematical tool but it is also a social science that can be used to analyze the behavior of rational nodes.[3, 4] In order to improve the wireless communication security in CRNs, many researchers have employed game theory to study potential cooperation among nodes.[5, 6]
In Ref. [5], the author proposed a game theoretic scheme in which users that have their own information to transmit can reinforce the secure communication of the primary link by acting as cooperative jammers if they are granted access to the spectrum to separately transmit their own data. In Ref. [6] the secondary transmitter (ST) cooperates with the primary transmitter (PT) to deliver information securely by relaying the PT’ s data, in return it is granted spectrum access opportunities. Both of these studies have assumed that cooperative nodes are trusted. If the cooperative nodes are malicious, it is possible for them to act as eavesdroppers. The cooperation between such nodes becomes complex[7, 8] because it is not clear if cooperation can enhance security.
In Ref. [9], a scenario was considered where an untrusted ST is willing to cooperate with the PT by relaying the PT’ s data for the chance of using the licensed spectrum. The cooperation takes effect but the ST has the opportunity to decode the PT’ s messages. An information-theoretic approach was adopted to solve this question. If the PT can secure the message from the STs by encoding a message into a codeword for the eavesdropping channel, then the ST will be allowed to relay the PT’ s data and transmit its own data. A different cognitive scenario was considered in Ref. [10], where the primary transmission must be secured from the secondary receiver. The ST is permitted to access the legitimate spectrum if it is willing to relay the PT’ s information or employ some Gaussian jamming to help the PT to lessen the probable leakage to the secondary receiver. First, the author found achievable rate regions and investigated several optimization problems. Furthermore, a Stackelberg game was employed to analyze the cooperation between the PT and STs. In Ref. [11], the STs work at half-duplex form, i.e., they can choose to either eavesdrop or transmit at any given time slot, and they prefer to transmit than eavesdrop. Hence, they are potential eavesdroppers on the primary traffic when they are not allowed to send their own data. Thus, it will increase the achievable secrecy rate for the PT to select an appropriate ST to transmit simultaneously. The author modeled the interaction between the PT and STs as a Stackelberg game in which the PT is a leader and the STs are followers. The drawback of this approach is that the STs only passively choose to eavesdrop or transmit with a fixed power level. This scheme works but it fails to fully exploit the rational and selfish features of multiple STs, which can lead to further improvement for the secrecy rate of the PT and the access chance of the STs.
In this paper, another kind of game theory: the second-price sealed-bid auction, [12, 13] is employed to model the interaction between the PT and untrusted STs, which are considered as the auctioneer and bidders, respectively. The bid is the achievable secrecy rate at the primary receiver (PR) when the bidder simultaneously transmits its own data with the PT. The strategy of each ST is its power choice, and the winning ST will be rewarded with the right of using the licensed spectrum and will only be required to provide the second largest bid. Because the STs prefer to transmit than eavesdrop, they will improve the PT’ s secrecy rate as far as possible. The main contributions of this work are summarized as follows: (i) With the proposed auction scheme, the hostile relationship between the PT and untrusted STs is transformed into a cooperative relationship. Therefore, the PT’ s secrecy rate and the STs’ access chance are both increased. (ii) An iterative algorithm based on the maxmin rule is proposed to find the optimal bidding power of STs for the access chance in the presence of multiple eavesdroppers.
The remainder of the paper is organized as follows. In Section 2, the system model is presented. In Section 3, the interaction between the PT and STs is modeled as the second-price sealed-bid auction, and some preliminaries are introduced. In Sections 4 and 5, we consider the cooperation between the PT and multiple STs using the proposed auction scheme and obtain the equilibrium. Simulation results are provided in Section 6, which is followed by the conclusion in Section 7.
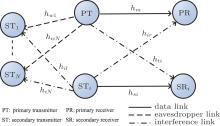
We consider a CRN model consisting of one primary pair and multiple secondary pairs (i = 1, 2, … , N), as depicted in Fig. 1.
The STs work at half-duplex mode, i.e., they can choose to eavesdrop or transmit, and they prefer to transmit than eavesdrop. Therefore, they are potential eavesdroppers on the primary transmission when they are not allowed to send their own data. It is assumed that the STs do not collude. Clearly, when the channel between the primary pair is worse than the eavesdropping channel, the secrecy rate is zero. In this model the receivers are assumed to regard the information from unintended transmitters as noise. In some cases the selected STs cause more interference to unselected STs; i.e., the eavesdroppers than to the PR. To improve the secrecy rate, the PT would select one appropriate ST to transmit simultaneously using the licensed spectrum.
The instantaneous power channel gain between the PT and PR is denoted as hm, between the PT and ST i as hwi, and between the ST i and ST j as hij. Similarly, we have hsi, hir, and hti as depicted in Fig. 1. The transmitted powers for the PT and ST i are Pp and Psi, respectively. The maximum transmitted power for the STs is Pmax. Without loss of generality, we assume that the noise power is the same for all of the links, denoted by σ 2. For better readability, the parameters of this paper are summarized in Table 1.
| Table 1. Parameters. |
If the ST i is selected by the PT, then other unselected STs eavesdrop as usual and the achievable secrecy rate at the PR in the presence of ST j is
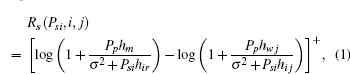
where [x]+ = max(x, 0). The achievable secrecy rate at the PR in the presence of all unselected STs is
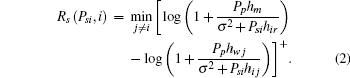
The achievable rate at the secondary receiver i is defined as

where Psi ≤ Pmax.
Throughout this paper the nodes are assumed to be rational and selfish.[14] Game theory is not only a proper mathematical tool but also a social science that can be used to analyze the behavior of such nodes. Auction, a kind of game theory, is a promising scheme to analyze how to realize efficient resource allocations in an environment where each bidder has its own preference. Auctions are generally classified into four types, which are: English auction (ascending price auction), Dutch auction (descending price auction), the first-price sealed-bid auction, and the second-price sealed-bid auction.[14] The former two auctions are open-outcry auctions because the bids of all of the bidders are disclosed to each other during the auction.[14] However, it is impossible that the private information (including the bid) of each ST is known by each other in the CRN. The latter two are sealed-bid auctions in which the privacy of the bidders is protected. When a sealed-bid auction is exploited to assign the object, the bidders submit bids simultaneously. The object is given to the bidder who submits the highest bid, in exchange for a payment. In a first-price sealed-bid auction scheme, the payment of the winning bidder is the price that it bids, and in a second-price sealed-bid auction scheme the payment of the winning bidder is the second highest bid among all of the bids. A second-price sealed-bid auction, which is known as a Vickrey auction, is individually rational for each bidder to bid truthfully with its own valuation, i.e., the maximum amount, it would like to pay for the object. To provide an intuitive understanding about this truthful bidding property, the winning opportunity of the bidder is reduced if the bid is less than its own valuation. If the bid is larger than its own valuation, then it would increase the winning opportunity of the bidder and its payoff would be negative. Moreover, such a truthful strategic choice is the dominant strategy equilibrium (DSE), which is defined as a strategy profile in which all of the players find the perfect strategy, no matter how the other players may play.[14] Therefore, in the DSE for a second-price sealed-bid auction, the strategy of every bidder is irrespective of the information on other bidders.
In summary, the second-price sealed-bid auction is employed to model the interaction between the PT and untrusted STs. The PT acts as the auctioneer and the STs are bidders. The object is the usage right of the licensed spectrum if it won the auction, and zero otherwise. The bidder’ s strategy is its transmitted power Psi and its utility is defined by
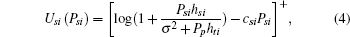
where csi is the cost per unit transmission power.
The bid of ST i is the secrecy rate defined by Eq. (2). This implies that the bidder i must know the PT’ s parameters hm and hwi (i = 1, 2, … , N). The PT sets the reserve price as
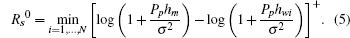
The PT only accepts a bid larger than Rs0.
The winning ST will be rewarded with the right of using the licensed spectrum and is only charged the second largest bid. Denoting the strategy of bidder i in the DSE as Psibid, the index of the winning bidder is

if Rs(Psv, v) > Rs0, otherwise no ST is chosen. In the case of multiple equal highest offers, it is resolved randomly. Furthermore, the second highest bid is

In order to find the DSE, in this subsection we will introduce some properties of the functions relevant to (1) and (4) in advance.
Denoting
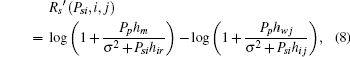
thus 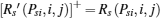
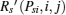
Theorem 1 For Psi ≥ 0, the function 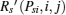
(i) If A(i, j) > 0, C(i, j) < 0, B(i, j) > 0, then 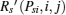
(ii) If A(i, j) > 0, C(i, j) < 0, B(i, j) ≤ 0, then 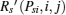
(iii) If A(i, j) ≥ 0, C(i, j) > 0, B(i, j) > 0, then 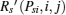
(iv) If A(i, j) < 0, C(i, j) > 0, B(i, j) > 0, then 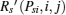
(v) When the above conditions are not satisfied, there is no proper value of Psi which makes 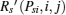
Here,
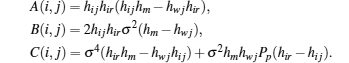
The first four cases are depicted in Fig. 2.
Proof Firstly, let 
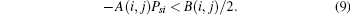
Secondly, set the derivative of 

The two solutions of Eq. (10) are
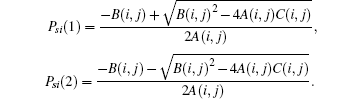
If A(i, j) > 0, C(i, j) < 0, and B(i, j) ≥ 0, then 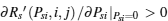

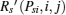
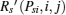
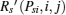
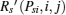
Other cases can be proved similarly.
Next, the properties of the winning bidder’ s utility Usi(Psi) are introduced by Theorem 2.
Theorem 2 The function Usi(Psi) (Psi ≥ 0) is concave in Psi and will be a positive value in the range of 0 ≤ Psi ≤ Psi0, if the following condition is satisfied:

where Dsi = ∂ Usi (Psi)/∂ Psi| Psi = 0, Psi0 is the nonzero solution of Usi(Psi) = 0 and csi is the cost per unit transmission power.
Proof It is easy to see that Usi (Psi) is concave in Psi and below zero when Psi → ∞ . Because Usi(0) equals zero, for the function Usi(Psi) to be a positive value over the range of 0 ≤ Psi ≤ Psi0, the condition Dsi = ∂ Usi (Psi)/∂ Psi| Psi = 0. > 0 must be satisfied.
According to Theorem 2, only the condition (11) is satisfied, and the ST i is willing to participate in the bidding.
In this section, the cooperation between the PT and two STs is presented using the second-price sealed-bid auction.
In such a case, when the ST i has won the auction, the achievable secrecy rate at the PR is

where j ≠ i. The utility of winning ST is defined as (4).
Assume 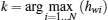

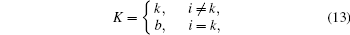
thus the ST K is the eavesdropper when the ST i simultaneously transmits with the PT.
When Dsi > 0, A(i, K) > 0, C(i, K) < 0, and B(i, K) > 0, the condition of Case 1 in Theorem 1 is satisfied, the ST i’ s cooperation can increase the achievable secrecy rate at the PR. From Fig. 2, it can be observed that in the case of Dsi > 0, A(i, K) > 0, C(i, K) < 0, and B(i, K) ≤ 0, Rs0 equals zero. In such a case, if Psi > − B(i, K)/2A(i, K), the achievable secrecy rate at the PR in the presence of ST K is larger than Rs0. In the case of Dsi > 0, C(i, K) > 0, B(i, K) > 0, the condition of Case 3 or 4 in Theorem 1 is satisfied. Under this circumstance, the security can be enhanced if i = k and the ST i simultaneously transmits with the PT. Above all, the achievable secrecy rate can be improved due to the ST i’ s cooperation if one of the following conditions is satisfied:

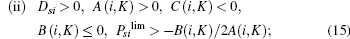
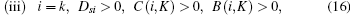
where
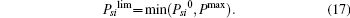
Recall that a second-price sealed-bid auction is individually rational for each bidder to bid truthfully with its own valuation, so they will bid with the maximum amount they would be willing to pay for the object. As mentioned in subsection 3.1, the game-theoretic concept of the DSE is such a truthful strategic choice.
On the basis of the above discussion, the dominant bidding strategy Psibid and the bid Rsibid of a bidder i (i = 1, 2) are given by Theorem 3.
Theorem 3 If one of the conditions (14)– (16) is satisfied, then the achievable secrecy rate Rs (Psi, i) can be improved due to a bidder i’ s cooperation. The dominant bidding strategy Psibid and the bid Rsibid of a bidder i (i = 1, 2) are given as
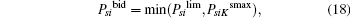
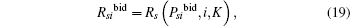
where K and Psilim are given by Eqs. (13) and (17), and PsiKsmax is expressed as
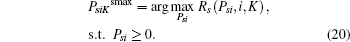
Proof Recall that the ST i likes transmitting better than eavesdropping, so it will do its best to improve the PT’ s secrecy rate to maximize its winning opportunity. As 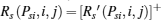
(i) Dsi > 0, A(i, K) > 0, C(i, K) < 0, B(i, K) > 0.
This case corresponds to Case 1 in Theorem 1. When PsiKsmax ≤ Psilim, the dominant strategy of ST i is bidding with PsiKsmax to maximize its winning opportunity as PsiKsmax maximizes Rs (Psi, i, K). When PsiKsmax > Psilim, PsiKsmax is out of the power range that the ST i can accept. Under this circumstance Rs (Psi, i, K) increases in the range of 0 ≤ Psi ≤ Psilim, so the dominant strategy of ST i is bidding with Psilim to improve its winning opportunity.
(ii) Dsi > 0, A(i, K) > 0, C(i, K) < 0, B(i, K) ≤ 0, Psilim > − B(i, k)/2A(i, k).
In the case of A(i, K) > 0, C(i, K) < 0, B(i, K) ≤ 0, if Psilim ≤ − B(i, K)/2A(i, K), the achievable secrecy rate at the PR in the presence of ST K is limited by Psilim and equal to Rs0, i.e., 0. When Psilim > − B(i, K)/2A(i, K), it can be proven as above.
(iii) i = k, Dsi > 0, C(i, K) > 0, and B(i, K) > 0.
Now K = b. This case corresponds to Case 3 or Case 4 in Theorem 1. From Fig. 2, it is easy to see that the dominant strategy of ST i is bidding with zero and PsiKsmax = 0. It is proved.
Remark 1 The scheme that we employed is a second-price sealed-bid auction, and the winning ST is only required to offer the second highest achievable secrecy rate. If the ST whose bidding strategy is zero wins the auction, then it can transmit with a power larger than zero.
Remark 2 When hwk = hwb, if one of the conditions (14) and (15) is satisfied, the achievable secrecy rate at the PR can be improved due to the ST i’ s cooperation and the ST i bids with the power of min(Psilim, PsiKsmax).
The index of the winning bidder v is defined as (6).
In traditional auction theory, the utilities of the auctioneer and the winning bidder are monotonically increasing and decreasing, respectively, as the price increases; namely, one’ s utility increase causes another’ s utility decrease. However, in this paper, because of their concavity, the utilities of the auctioneer and winning bidder v (i.e., Rs (Psv, v) and Usv (Psv)) may have the same monotonicity in some specific ranges of Psv, as shown in the red dashed rectangular areas of Fig. 3. Hence, we will introduce a modification of the second-price sealed-bid auction:[5] the winning bidder is charged at least the second highest bid by the auctioneer. In this setting, it can be seen from Fig. 3 that the winning bidder v may select a proper transmitted power to maximize its utility Usv (Psv) with the limitation Rs (Psv, v) ≥ Rs2, which can bring the simultaneous increase of Rs (Psv, v) and Usv (Psv). It is worth noting that this modification does not harm the benefits of the auctioneer and bidder, even if their concavity is not satisfied.
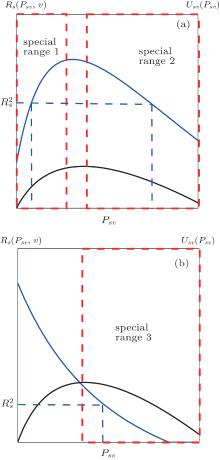 | Fig. 3. Illustration of the auction scheme’ s modification. (a) Case 1 or case 2 in Theorem 1; (b) case 3 or 4 in Theorem 1. |
In short, the outcome of this auction is given by Theorem 4.
Theorem 4 The proper power Psv* selected by the winning ST v is

where Rs2 is given by (7), and Psvopt is the power maximizing utility of the winning ST v and can be expressed as

Psh and Psl (the winning ST’ s transmitted power levels which make the achievable secrecy rate equal to Rs2) are given by (i) If Rs(0, v) ≥ Rs2, then Psl = 0; otherwise, Psl is the solution of Rs (Psv, v)) = Rs2 lying in the range of 0 < Psv < Psvbid; (ii) If Rs (Psvlim, v)) ≥ Rs2, then Psh = Psvlim; otherwise, Psh is the solution of Rs (Psv, v)) = Rs2 lying in the range of Psvbid < Psv < Psvlim.
Proof Recall that the winning ST v is charged at least the second highest bid by the PT, so it will maximize its utility Usv(Psv) on the basis that the utility of the PT Rs (Psv, v) is no less than Rs2, and its selection for Psv* is illustrated in Fig. 4.
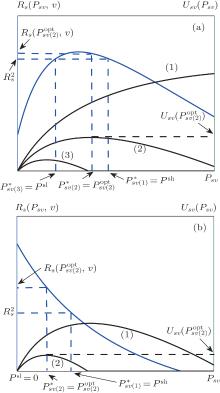 | Fig. 4. Illustration of Theorem 4. (a) Case 1 or case 2 in Theorem 1. (b) Case 3 or case 4 in Theorem 1. |
If traditional auction theory is employed in our system model, then the utilities of the PT and winning ST v are Rs2 and Usv (Psl)(or Usv (Psh)), respectively. From formula (21) and Fig. 4, for the case Psl ≤ Psvopt ≤ Psh, it can be seen that the modification of the second-price sealed-bid auction increases these two utilities to Rs(Psvopt, v)) and 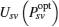
In this section, we consider the cooperation between the PT and more than two STs using the modified second-price sealed-bid auction. In this case, if the ST i has won the auction, then the PT transmits with the help of ST i in the presence of multiple eavesdroppers, i.e., unselected STs. The achievable secrecy rate at the PR is defined as (2). The utility of the winning ST is defined as (4).
Recall that the ST i will do its best to improve the PT’ s secrecy rate to maximize its winning opportunity, so Psibid is the solution of the following max– min problem:
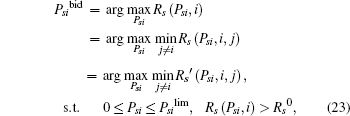
where Rs (Psi, i), Rs (Psi, i, j), and 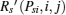
Therefore, the dominant bidding strategy Psibid and the bid Rsibid of a bidder i (i = 1 … N, N ≥ 3) are given by Theorem 5.
Theorem 5 If one of the conditions (14)– (16) is satisfied, then the achievable secrecy rate Rs (Psi, i) can be improved due to a bidder i’ s cooperation. The dominant bidding strategy Psibid and the bid Rsibid of a bidder i (i = 1 … N, N ≥ 3) are given by Algorithm 1.
Proof Similar to Section 4, the achievable secrecy rate Rs (Psi, i) may be larger than Rs0 if one of the conditions (14)– (16) is satisfied.
Let 
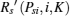
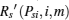
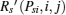
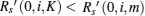


Assume Psira > Psiinter(K, m) and
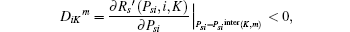
then 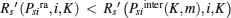



i.e., 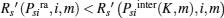
Above all, the values of DiKm and DimK can be divided into three categories: i) DiKm < 0, DimK < 0; ii) DiKm > 0, DimK < 0; and, iii) DiKm > 0, DimK > 0.
To solve the max– min problem (23), two situations are analyzed according to the values of A(i, K), B(i, K), C(i, K), Dsi, and k.
(i) i = k, Dsi > 0, C(i, K) > 0, and B(i, K) > 0.
If Dsi > 0, C(i, K) > 0, and B(i, K) > 0, the condition of Case 3 or Case 4 in Theorem 1 is satisfied. It is seen from Fig. 2 that DiKm < 0 and 
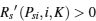
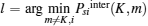
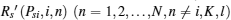
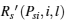
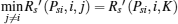


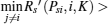
(ii) Dsi > 0, A(i, K) > 0, C(i, K) < 0.
As mentioned above, we can get 
Firstly, we assume the situation that DiKm > 0 and DilK > 0 does not happen. Let Psiinter0 = 0, three different cases are analyzed according to various situations of the intersection Psiinter(K, l).
(i) Psiinter(K, l) ∉ (Psiinter0, Psilim] or 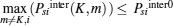
In such a case, the optimization problem (23) can be expressed as (24).
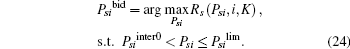
Hence, Psibid = min (Psilim, PsiKsmax), Rsibid = Rs (Psibid, i, K).
(ii) DiKl < 0 and DilK < 0, Psiinter(K, l) ∈ (Psiinter0, Psilim].
As DilK < 0, the function 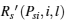
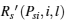
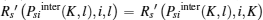

Then, we can reformulate (23) as
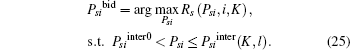
As DiKl < 0 and Rs (Psi, i, K) is concave in Psi for Psi > Psiinter0, the solution of (25) is Psibid = min(Psilim, PsiKsmax).
(iii) DiKl > 0 and DilK < 0, Psiinter(K, l) ∈ (Psiinter0, Psilim].
Similarly, in this case the problem (23) is rewritten as (25). As DiKl > 0 and 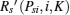
In such a case, it can be observed from Fig. 2 that 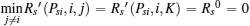
Next, we consider the case of DiKl > 0 and DilK > 0.
(iv) DiKl > 0 and DilK > 0, Psiinter(K, l) ∈ (Psiinter0, Psilim].
As DiKl > 0 and DilK > 0, 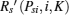
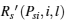

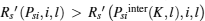
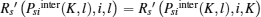

Because 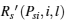
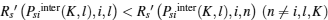
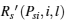
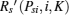
All of the above steps can be summarized as Algorithm 1 “ maxmin algorithm for the dominant strategy equilibrium” .
Because N and Psilim are both finite values, the problem (23) must have a solution if one of the conditions (14)– (16) is satisfied.
Remark 3 Similar to Remark 2, in a case where there are multiple equal largest hwi, the ST who meets the condition (14) or (15) bids according to Algorithm 1, but the ST who meets the conditions (16) quits from the bidding.
Remark 4 In Algorithm 1, the arrays PsiL and RsiL are used to record the power value and the achievable secrecy rate corresponding to the intersections lying on the curve 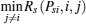
The index of the winning bidder v is defined as (6). It has to provide the PT, at least Rs2, given by Eq. (7).
Similar to Algorithm 1, Algorithm 2 is used to calculate the information of the intersections lying on the curve 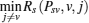

Similar to subsection 4.2, the modified second-price sealed-bid auction scheme is employed and the outcome of the auction is given by Theorem 6.
Theorem 6 The proper power Psv* selected by the winning ST v is

where Rs2 and Psvopt are given by (7) and (22), respectively, PSH and PSL (the winning ST’ s transmitted power levels which make the achievable secrecy rate exactly equal to Rs2) are given by (i) If RsvL(1) ≥ Rs2, then PSL = 0; otherwise, if RsvL(T) < Rs2 ≤ RsvL(T + 1) (1 ≤ T < tv), let x = LRN(T), then PSL is the solution of Rs(Psv, v, x) = Rs2; (ii) If RsvR(wv) ≥ Rs2, then PSH = Psvlim; otherwise, if RsvR(W) < Rs2 ≤ RsvR(W − 1), (1 < W ≤ wv), let y = RLN(W), then PSH is the solution of Rs (Psv, v, y) = Rs2.
Proof The proof is similar to Theorem 4 but there are some differences from Theorem 4 in the selection for PSH and PSL. Recall that the arrays PsvL and RsvL have recorded the power value and the achievable secrecy rate corresponding to the intersections lying on the curve 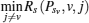
One illustration of the selection for PSH and PSL is shown in Fig. 5. In Fig. 5, the thick curve indicates the value of 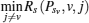
In this section, we present the numerical results to illustrate the proposed auction scheme. We consider a simple geometrical model where the STs are all placed at approximately the same normalized distance from the PT and the PR. A flat Rayleigh fading environment is considered, with the average power channel gains are given by E[hm] = E[hsi] = E[hwi] = 1, E[hij] = E[hir] = E[hti] = 0.1, Pp, Pmax, and noise power σ 2 are set to 10 mW, 10 mW, and 1 mW, respectively. The cost per unit transmission power csi is set to be c, as shown in the figures. The displayed results are obtained through 105 trials.
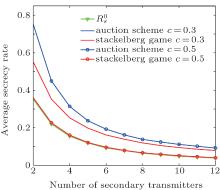
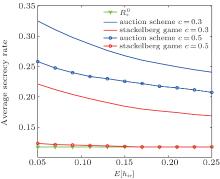
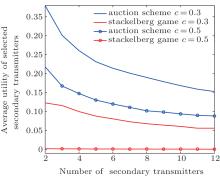
Figures 6– 8 show the average secrecy rate of the PT versus the number N of STs, the average eavesdropping power channel gain hwi and the average interference power channel gain hir, respectively, using our proposed auction scheme and the Stackelberg scheme proposed in Ref. [11]. Figures 9– 11 demonstrate the average utility of the selected ST as a function of the number N of STs, the average eavesdropping power channel gain hwi and the average interference power channel gain hir, respectively, using the same two schemes. In Figs. 7– 8 and Figs. 10– 11, the parameter N is set to 5.
From Figs. 6– 11, it is seen that both two schemes can improve the average secrecy rate of the PT and the average utility of the selected ST compared with a situation where no ST is selected. It is worth noting that the utilities and rates of STs which are not selected are zero. When the Stackelberg scheme is used, the STs can only choose to eavesdrop or transmit with a fixed power Pmax. The larger cost per unit transmission power csi leads to a higher possibility that the utility of the selected ST is not positive. The STs may be willing to eavesdrop for a large enough csi. In the case of csi = 0.5, the Stackelberg scheme could hardly improve the performance of the PT and the selected ST. Due to competitiveness of the STs, greater performance improvements are achieved for the PT with our proposed auction scheme than with the Stackelberg scheme proposed in Ref. [11], as shown in Figs. 6– 8. A similar phenomenon holds for the performance of the selected ST as shown in Figs. 9– 11 because our auction scheme increases the access chance of the STs.
 | Fig. 10. Average utility of the selected ST versus average power channel gain hir. |
 | Fig. 11. Average utility of the selected ST versus average eavesdropping channel gain hwi. |
As the number of STs increases, the average secrecy rates with these two schemes obviously decrease, as shown in Fig. 6, since the number of eavesdroppers increases at the same time. A similar case holds for the selected ST’ s performance due to competitiveness, as shown in Fig. 9.
With the increase in the interference power channel gain hir, the advantage of these two schemes diminishes, as shown in Figs. 7 and 10, because the selected ST causes more interference to the PR. This implies that the larger values of hir compared to hij benefit these two schemes.
Above all, significant performance improvements can be achieved for the PT and the selected ST with our proposed scheme.
In this paper, we considered a scenario in which the multiple half-duplex STs threaten the security performance of the primary link by eavesdropping when they are not allowed to use the licensed spectrum.
A modified second-price sealed-bid auction scheme was proposed to analyze the interaction between the PT and untrusted STs. With the presented scheme, the PT and STs became allies instead of foes. Based on the max– min rule, an iterative algorithm was proposed to find the optimal bidding power of the STs in the presence of multiple eavesdroppers. If a proper ST is granted to access the licensed spectrum, it will help the PT to enhance the security by creating more interference to other unselected STs than to the PR. Numerical results show that both the PT and the selected ST can achieve significant performance improvements with our proposed scheme because it not only helps the PT select one proper cooperating ST but also increases the access chance of the STs. In our further work, the scenario in which the power of the PT can be adjusted will be investigated.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|