†Corresponding author. E-mail: yfnie@nwpu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 11471262), the National Basic Research Program of China (Grant No. 2012CB025904), and the State Key Laboratory of Science and Engineering Computing and the Center for High Performance Computing of Northwestern Polytechnical University, China.
We study the hyperbolic–parabolic equations with rapidly oscillating coefficients. The formal second-order two-scale asymptotic expansion solutions are constructed by the multiscale asymptotic analysis. In addition, we theoretically explain the importance of the second-order two-scale solution by the error analysis in the pointwise sense. The associated explicit convergence rates are also obtained. Then a second-order two-scale numerical method based on the Newmark scheme is presented to solve the equations. Finally, some numerical examples are used to verify the effectiveness and efficiency of the multiscale numerical algorithm we proposed.
In recent years, composite materials have been widely used in engineering applications owing to their attractive physical and mechanical properties. Due to large heterogeneities (caused by inclusions or holes) in the composite structures (see Fig. 1 for example), the direct numerical computation of the composite materials needs a huge amount of computational resources and a prohibitive amount of computational time because it requires a very fine mesh to capture the micro-scale behavior. Fortunately, mathematicians and engineers have developed some multiscale methods to solve this difficult problem in the past thirty years, such as the asymptotic homogenization method (AHM), heterogeneous multiscale method (HMM), variational multiscale method (VMS), and multiscale finite element method (MSFEM). We refer the interested readers to Ref. [1] for the details. The basic idea of the homogenization method is to give the global equivalent behavior of the composite structure by smoothing the micro-scale fluctuations due to the heterogeneities. However, small periodic parameter ε , while small, often does not reach zero in many engineering applications. At this time, the numerical accuracy of the standard homogenization method may not meet the actual need (see Refs. [2]– [11]). To this end, multiscale asymptotic methods and associated numerical algorithms are developed to capture the microscopic properties of the composite materials. The main idea of the multiscale asymptotic methods is to add corrector terms to the homogenized solution (see Refs. [2]– [11]).
 | Fig. 1. The whole domain Ω and the unit cell Y.[1] |
To the best of our knowledge, hyperbolic– parabolic equations with rapidly oscillating coefficients have a wide range of practical applications in composite structures, which describe the wave scattering and diffraction with damping in a heterogeneous medium (see Refs. [12]– [14]). In addition, the hyperbolic– parabolic equations are the model equations of nonclassical heat conduction problems under the ultra conventional heating (cooling) condition. This model is widely used in the fields of micro-electro-mechanical systems, laser, and aerospace technology (see Ref. [15]). Therefore, it is significant to study the hyperbolic– parabolic equations with rapidly oscillating coefficients. The homogenization of the linear hyperbolic– parabolic equations in the perforated domains can be found in Ref. [12]. In addition, an asymptotic analysis for a weakly damped wave equation in an elastic problem can be found in Ref. [13]. The author proved a homogenization theorem for the weakly damped wave equation. Besides, the authors in Ref. [16] analyzed the effective behavior of the solution of a wave equation with interior and boundary damping defined in a periodical perforated medium. The analysis of this problem is more difficult than that in Ref. [12]. Moreover, the homogenization of the weakly damped nonlinear hyperbolic– parabolic equations was studied in Ref. [17]. The author proved that the solutions of a class of highly oscillatory nonlinear evolution problems converge to the solution of a homogenized quasilinear hyperbolic– parabolic problem based on the sigma-convergence method. On the other hand, there is much literature focusing on the concern weighted (in time) and pointwise (in time) energy decay estimates of the damped wave equations (see Refs. [14] and [18]– [20]). In summary, the current research on the hyperbolic– parabolic equation with damping mainly focuses on the homogenized analysis and the energy decay estimates.
In this paper, we focus on the second-order two-scale analysis for the hyperbolic– parabolic equations with rapidly oscillating coefficients in order to capture the micro-scale behavior. To our knowledge, it is difficult to obtain the explicit convergence rate for the wave equation with non-homogeneous boundary condition, because it is extremely difficult to obtain explicitly a prior estimate of the solution (see Refs. [6] and [7]). Therefore, obtaining the explicit convergence rate for the hyperbolic– parabolic equation will be a more difficult problem. The main idea of this paper is to impose the homogeneous Dirichlet boundary conditions on the auxiliary cell problems (see Refs. [4]– [10]). If Ω is the union of the entire periodic cells, the second-order two-scale solution of problem (1) will satisfy automatically the boundary conditions on ∂ Ω . In this case, we can obtain the explicit convergence rate and improve the error estimate order of the second-order two-scale solution under some extra assumptions. The main result of this paper is Theorems 3 and 4 in Section 3. Surprisingly, the error estimate of the hyperbolic– parabolic equations can devolve back to the error estimate of the hyperbolic equation.
This paper is organized as follows. In Section 2, the detailed construction of the second-order two-scale solution to the hyperbolic– parabolic equations is given by multiscale asymptotic analysis. In addition, we give the error analysis in the pointwise sense of first-order two-scale solution and second-order two-scale solution. Through the above analysis, we theoretically explain the importance of the second-order solution in capturing the micro-scale oscillating information. In Section 3, we derive the explicit convergence order of the second-order two-scale solution. From the convergence results, we can easily obtain the convergence conclusion for the hyperbolic equation. In Section 4, we give the finite element approximation schemes for the auxiliary cell problems and the homogenization problem of the hyperbolic– parabolic equations. After that, we present a second-order two-scale numerical method to solve the hyperbolic– parabolic equations based on the Newmark scheme (see Ref. [21]) and the average technique (see Ref. [2]), and give a detailed comparison and analysis of the computational efficiency and stability between the second-order two-scale method and the direct finite element method. In Section 5, some numerical examples are given, which illustrate our method. Finally, the conclusions are given in Section 6.
For convenience, we use the Einstein summation convention on repeated indices in this paper.
Consider the initial-boundary value problems of the hyperbolic– parabolic equations with rapidly oscillating coefficients as follows:

where Ω is a bounded convex domain in ℝ n(n = 2, 3) with a boundary ∂ Ω , and f(x, t), ϕ (x, t), u0(x), u1 (x) are given functions. The coefficient ρ ε (x, t) and the matrix 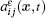
At first, we set y = x/ε and make the following hypothesis to obtain a series of conclusions:
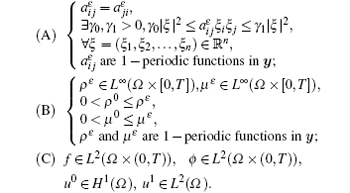
In this section, we first give the specific construction process of the first-order two-scale asymptotic solution and the second-order two-scale asymptotic solution to the problem (1). In order to save the length of article, we denote the first-order two-scale solution and the second-order two-scale solution as FOTS and SOTS, respectively. The error analysis in the pointwise sense of FOTS and SOTS is also given, which neatly illustrates the extreme necessity of SOTS. We analyze the error in the pointwise sense first because it will give the residual equations which is of vital significance for error analysis in the integral sense.
To the problem (1), we suppose that uε (x, t) can be expressed in the following asymptotic form:

Due to y = x/ε ∈ Y (Y is the unit cell, where Y = (0, 1)n, n = 2, 3), the chain rule can be denoted as 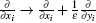

After that, a series of equations are obtained if the coefficients of ε i (i = − 2, − 1, 0, 1, … ) from both sides of Eq. (3) are set to be equal to each other, which are listed as follows:
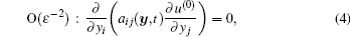

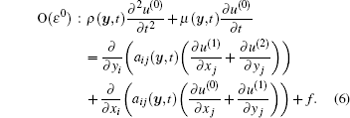
Now we solve the asymptotic expansion terms recursively. Firstly, applying the standard asymptotic homogenization theory to Eq. (4), we know that the first term of the asymptotic expansion (2) only depends on macroscopic scale x, which can be expressed as u(0) = u(0)(x, t).
Secondly, it can be easily recognized that equation (5) is linear with respect to u(0), so u(1) can be defined as

where Nα 1(x, y, t) is the first-order auxiliary cell function defined in unit cell Y. Substituting u(1) into Eq. (5), we obtain the following equation with attaching boundary condition:
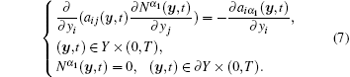
Remark 1 According to Lax– Milgram theorem and assumption (A), it is easy to prove that problem (7) has the unique solution for any fixed time variable t.
Then, inspired by Refs. [7] and [11], we can be define the homogenized material coefficients 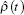

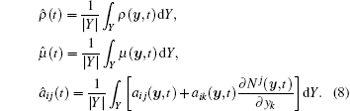
Further, we can define the homogenized problem as follows:
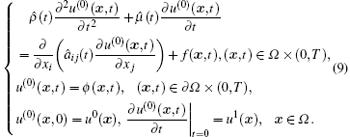
Remark 2 Under assumptions (A) and (B), we can prove that the homogenized coefficient tensor â ij(t) is symmetric, positive-definite, and bounded (see Ref. [7]). Besides, it is easy to prove that 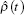
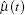
Finally, from Eqs. (6) and (9), the following equation is obtained:

Thus u(2) can be defined as follows:
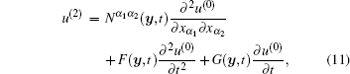
where Nα 1α 2(y, t), F(y, t), and G(y, t) are the second-order auxiliary cell functions defined in unit cell Y. Substituting Eq. (11) into Eq. (10), we obtain a series of equations which attach the zero boundary condition
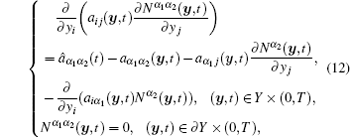
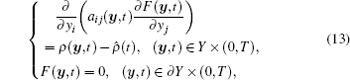
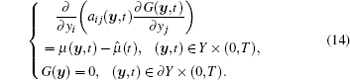
Remark 3 According to the Lax– Milgram theorem and assumptions (A) and (B), it is easy to prove that problems (12)– (14) have a unique solution for any fixed time variable t.
Summing up, we define the FOTS and SOTS of problem (1) as follows:

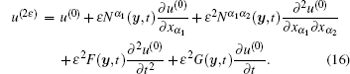
Notably, the difference from the wave equation in Ref. [7] lies in that there exist second-order auxiliary cell functions F(y, t) and G(y, t) which are used to eliminate the effects of the inertial term and the damping term.
Theorem 1 The hyperbolic– parabolic equations (1) with rapidly oscillating coefficients have an SOTS approximate solution as follows:
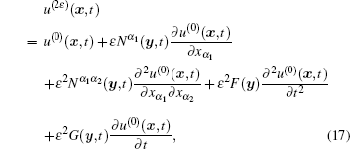
where u(0) is the solution of the homogenized problem (9), Nα 1 is the first-order auxiliary cell function defined by Eq. (7), and Nα 1α 2, F, and G are the second-order auxiliary cell functions defined by Eqs. (12)– (14), respectively.
In this subsection, we give the specific error analysis of FOTS and SOTS in the pointwise sense. Firstly, we denote the error functions of FOTS and SOTS as ω (1)(x, t) = u(ε )(x, t) – u(1ε )(x, t) and ω (2)(x, t) = u(ε )(x, t) – u(2ε )(x, t). Suppose that Ω is the union of the entire periodic cells, i.e., 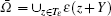
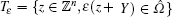
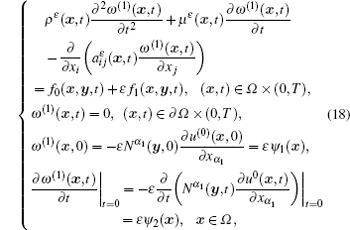
where
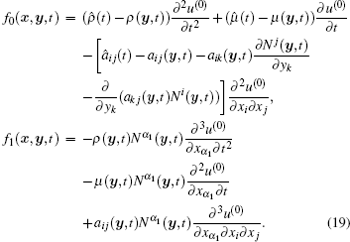
Secondly, using the same method, we derive the following residual equation of SOTS which holds similarly in the distribution sense:

where

Now we can give a conclusion about the error analysis in the pointwise sense. From the residual equation (17), one easily finds that the residual of FOTS is O(1) in the pointwise sense due to the term f0(x, y, t). This is not acceptable in practical engineering calculation. However, it is easy to see from the residual equation (18) that the residual of SOTS is O(ε ) in the pointwise sense. Thus, the SOTS can have the required accuracy for engineering calculations and capture the the micro-scale behavior of composite materials when ε is a sufficiently small constant. This is the main reason and motivation to develop the SOTS.
In this section, we give the proof of the explicit convergence order of SOTS in the integral sense for the hyperbolic– parabolic equations with rapidly oscillating coefficients. Moreover, we give the degradation of the hyperbolic– parabolic equation’ s error estimate. In order to obtain the explicit convergence order of SOTS, we need to give some lemmas first.
As we all know, the auxiliary cell functions are defined with the periodic boundary conditions in the classical homogenization methods (see Refs. [22]– [24]). In this case, the auxiliary cell functions have enough regularity on the boundary of the unit cell. However, the normal derivatives of the auxiliary cell functions defined with the Dirichlet boundary conditions only are continuous on the boundary of the unit cell under the geometric symmetry and regularity assumptions of the hyperbolic– parabolic equation’ s coefficients (see Refs. [4]– [10]).
To obtain the regularity of the cell functions, we make the following assumptions similar to Refs. [6]– [10]: (i) (ii) let Δ 1, … , Δ n (n = 2, 3) be the middle superplanes of the reference cell Y = (0, 1)n, then set y = x/ε and assume that aii(y, t), ρ (y, t), μ (y, t) are symmetric with respect to Δ 1, … , Δ n(n = 2, 3) and aij(y, t), i ≠ j are anti-symmetric with respect to Δ 1, … , Δ n (n = 2, 3) in Y for any fixed t ∈ [0, T].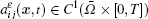
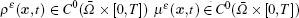
Lemma 1 Under assumptions (A)– (C) and (i) and (ii), the normal derivatives σ Y(Nα 1), σ Y(Nα 1α 2), σ Y(F), and σ Y(G) can be proved to be continuous on the boundary for any fixed t ∈ [0, T] by using the same method in Refs. [6]– [10], where operator 
Theorem 2 Suppose that Ω ⊂ ℝ n is the union of the entire periodic cells, i.e., 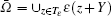

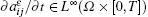
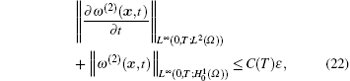
where C(T) is a constant independent of ε , but dependent on T.
Proof Firstly, from Eqs. (7), (8), and (12)– (14), we have the following result:
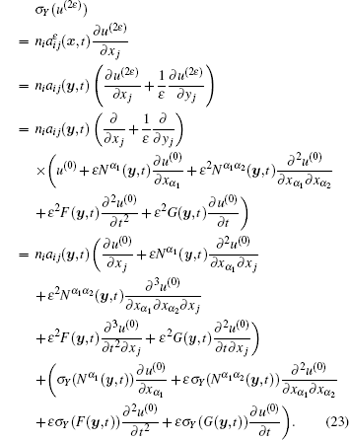
This formula will be used in the following proof.
Secondly, we use the residual equation (18) to complete the error estimate of SOTS for the hyperbolic– parabolic equations with rapidly oscillating coefficients. Since ∂ ω (2)/∂ t is in L∞ (0, T; L2(Ω )), we cannot use ∂ ω (2)/∂ t as the test function for residual equation (18) directly. To overcome this difficulty, we use the density argument (see Refs. [6], [7], and [24]). In order to simplify the process of proof, we omit this detail. Then, multiplying ∂ ω (2)/∂ t on both sides of Eq. (18) and integrating by parts on Ω , we obtain
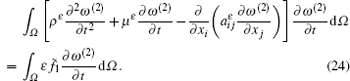
Using Green’ s formula to simplify the above identity (21), we obtain
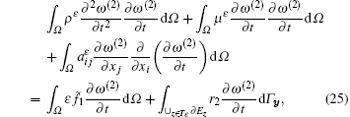
where r2 results from using the Green’ s formula on ∂ Ez (see Refs. [25] and [26]).
Combining Eq. (20) and Lemma 2, we obtain
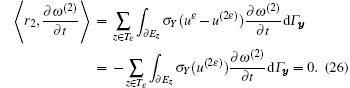
After that, we can easily derive the following identity by combining Eqs. (22) and (23):
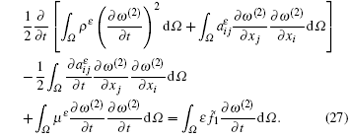
Then, we integrate both sides from 0 to t (0 < t ≤ T) and obtain
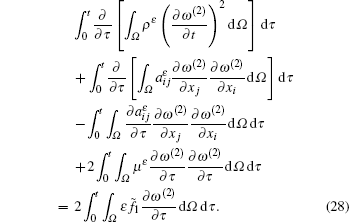
After a simple calculation, we obtain the following equation:
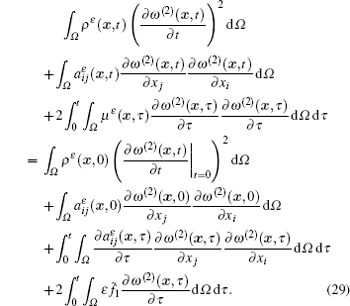
Then substituting the initial conditions and the boundary conditions of residual equation (18) into the above identity (26), we have
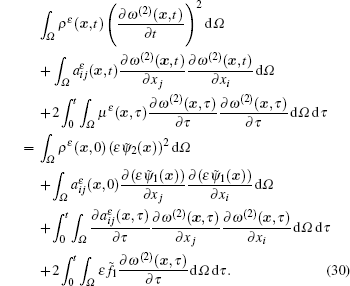
So far, we have obtained the essential identity for Theorem 3. Starting from here, we will give the final proof. First of all, owing to assumptions (A) and (B) and using the Poincaré – Friedrichs inequality, we have the following inequality by transforming the left side of Eq. (27):
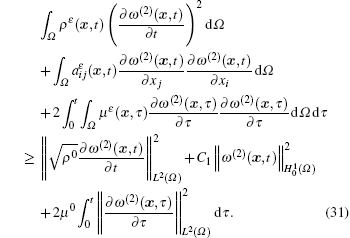
Then, due to 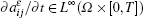

After that, using the Young’ s inequality ab ≤ (λ a2 + λ b2/λ )/2, ∀ λ ∈ ℝ + with parameter λ and assumptions (A)– (C), and choosing the same parameter λ at ∀ τ ∈ [0, T], we obtain the following inequality by transforming the right side of Eq. (27):

Choosing a sufficiently big λ > 0 fulfilled λ − 2μ 0 > 0 and combining Eqs. (28) and (30), we have
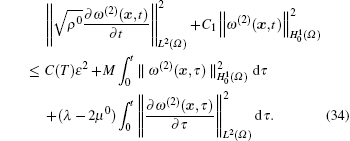
Denoting δ 1 = min(ρ 0, C1) and δ 2 = max(M, λ − 2μ 0), we have
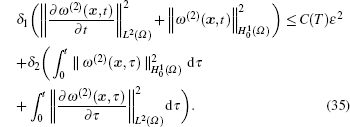
Without loss of generality, we denote C(T) = C(T)/δ 1 and δ = δ 2/δ 1 and obtain the following inequality:
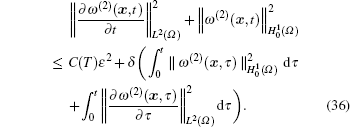
Setting
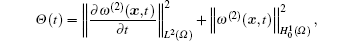
then we obtain 
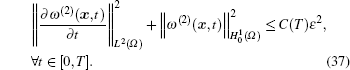
Then by using the AM– GM inequality 
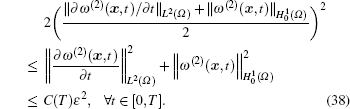
With the arbitrariness of time variable t and squaring root on both sides of inequality (35), we obtain the final convergence result

where C(T) is a constant independent of ε , but dependent on T.
In this section, we give the SOTS’ s convergence theorem of the hyperbolic equation by the degradation of Theorem 2. In general, for ρ ε ≠ 0 and μ ε = 0, equation (1) is called the hyperbolic wave equation, which describes the wave scattering and diffraction behavior of the composite structure. In the past, the convergence analysis of the hyperbolic equation is done separately. Now, we can obtain the convergence results of the hyperbolic equation from the degradation of Theorem 2.
Theorem 3 Assume that the definitions of Ω , 


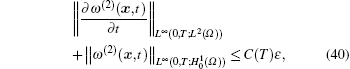
where C(T) is a constant independent of ε , but dependent on T.
Proof Under the situation of ρ ε ≠ 0 and μ ε = 0, the term 

where the constant μ 0 = 0 due to μ ε = 0.
Then using the same proof method and denoting δ 1 = min(ρ 0, C1) and δ 2 = λ , we can obtain the following inequality:
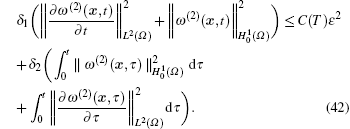
After that, using Gronwall’ s inequality (see Ref. [6] and [7]) and AM– GM inequality 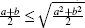
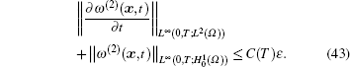
The obtained convergence result of the hyperbolic wave equation is in completely accord with that in Ref. [7].
In this section, we firstly give the finite element approximation schemes for the auxiliary cell problems and the homogenization problem of hyperbolic– parabolic equations (1). Then, we present a second-order two-scale numerical method to efficiently solve hyperbolic– parabolic equations (1).
It is easy to see that auxiliary cell problems (7) and (12)– (14) are all elliptic equations, where the time variable t only plays the role of a parameter. So we can solve these auxiliary cell problems with the standard finite element method. Considering the internal geometric structure complexity of the unit cell, we should use the triangular element in ℝ 2 and the tetrahedral element in ℝ 3 to solve the auxiliary cell problems. Without loss of generality, we only discuss the two-dimensional problem in this paper. Let Jh = {K} be a regular family of triangulation of the reference unit cell Y, where h = maxK{hK}. Define the linear conforming finite element space for solving the auxiliary cell problems as 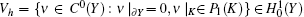
As we all know, the homogenized coefficients â ij(t) are derived from Eq. (8). So â ij(t) depend on the finite element calculation of the auxiliary cell problem Nα 1(y, t). Suppose that 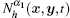
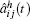
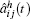
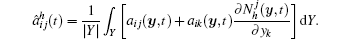
Therefore, we need to solve the following modified homogenized equation:

According to our knowledge, the numerical accuracy of the modified homogenization problem (41) directly affects the accuracy of SOTS. To improve the accuracy of the modified homogenization problem (41), we solve the modified homogenized equation with the quadratic element. Let Jh0 = {e} be a regular family of triangulation of the spatial region Ω , where h0 = max{he}. Define the quadratic finite element space as 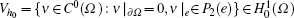
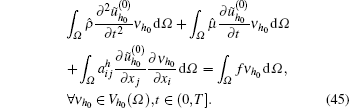
Secondly, let 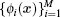
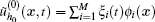
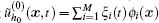
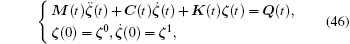
where ζ (t) = [ξ 1(t), ξ 2(t), … , ξ M(t)]T, M(t), C(t), and K(t) are the mass matrix, the damping matrix, and the stiffness matrix, respectively, and Q(t) is the load vector (see Ref. [21]), which can be obtained by the following expressions:
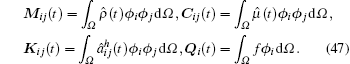
Now, we introduce the Newmark scheme for solving the ordinary differential system (44). As we all know, the Newmark difference scheme is an unconditional stable and convergent difference scheme when scheme parameters δ ≥ 0.5 and α ≥ 0.25 (δ + 0.5)2 (see Refs. [21] and [25]) and we choose δ = 0.5 and α = 0.25 in this paper. On the other hand, from Theorem 1, we know that the calculation of SOTS needs the values of acceleration ∂ 2u(0)/∂ t2 and velocity ∂ u(0)/∂ t at every time step. The Newmark scheme not only can solve u(0), but also simultaneously solve ∂ 2u(0)/∂ t2 and ∂ u(0)/∂ t. So we use the Newmark scheme to solve the ordinary differential system (43) at any time step. The detailed procedure of the Newmark scheme for system (43) is listed as follows.
Step 1 Construct mass matrix M(t), damping matrix C(t), stiffness matrix K(t), and load vector Q(t).
Step 2 Use the initial and boundary conditions ζ (0) = ζ 0 and 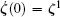
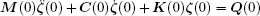
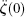
Step 3 Choose the time step Δ t and parameters δ , α . For each time step, we should know ζ (t), 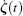
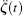
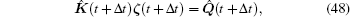
where

Finally, we can derive 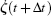
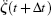
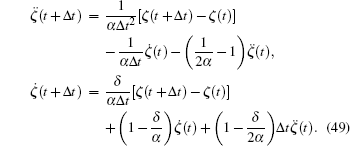
Step 4 Repeat step 3 for all time steps, then we can obtain the value of the ordinary differential system (43) at any time step.
In this subsection, we present a second-order two-scale numerical method to efficiently solve the hyperbolic– parabolic equations with rapidly oscillating coefficients. Firstly, we give the algorithm of the second-order two-scale numerical method. After that, we give the analysis of SOTS’ s computational efficiency and superiority to explain why the second-order two-scale numerical method can greatly reduce the calculation compared with the direct finite element method.
Step I Generate a geometric model of the unit cell and compute auxiliary cell functions 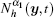
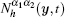
Step II Calculate the homogenized coefficients 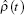
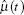

Step III Solve the spatial variable derivatives ∂ ũ (0)/∂ xα 1, ∂ 2ũ (0)/∂ xα 1∂ xα 2 of the homogenized solutions ũ (0)(x, t) by the average technique on relative elements (see Refs. [2] and [6]) and the temporal variable derivatives ∂ ũ (0)/∂ t, ∂ 2ũ (0)/∂ t2 by using the difference schemes (46) in subsection 4.1. The following formulas are used for evaluating the high order partial derivatives of the spatial and temporal variables:
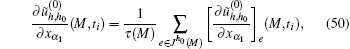
where M is the node of FEM set Jh0, Jh0(M) denotes the set of elements with the same node M, τ (M) is the number of elements in Jh0(M), 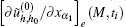
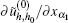
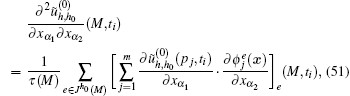
where m is the number of node freedom on element e, and 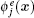
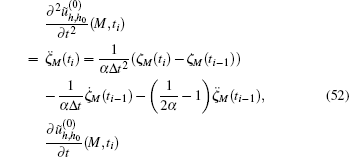

where ζ M(ti) denotes the value of node M at time t = ti, 

Step IV Use the auxiliary cell functions in step 1 to assemble SOTS as follows:
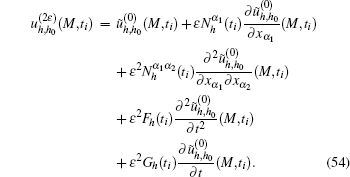
Step V For arbitrary point (x, t) ∈ Ω × [0, T], we use the higher-order interpolation method to obtain the high-precision SOTS value as follows:
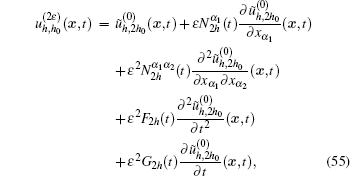
where
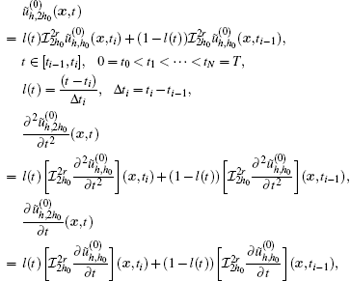
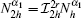

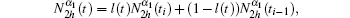
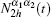
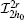
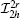
The main motivation to develop multiscale methods is to solve the problems which cannot be solved by the conventional numerical methods. So the analysis of the computational efficiency of multiscale methods only can be done when we assume that the multiscale problems can be solved by the conventional numerical methods. Firstly, we give a specific analysis to explain why the SOTS can greatly reduce computational cost compared with the direct FEM. We assume that the whole domain Ω consists of n × n entire periodic cells. If we need m elements to mesh every unit cell in Ω , the total number of elements is n × n × m in the direct FEM calculation. Fortunately, SOTS only needs the grid information of a single cell to solve the auxiliary cell problems. From Section 2, we know that there are two auxiliary cell problems Nα 1(y, t), four Nα 1α 2(y, t), one F(y, t), and one G(y, t) for the two-dimensional hyperbolic– parabolic equations. Thus, the total number of elements to solve the auxiliary cell problems is 8m. Luckily, this number does not increase even if the cell number of the whole domain Ω increases. On the other hand, we assume that the elements for solving the homogenization problem is c × n × n × m (0 < c ≪ 1). In the general calculation, c is in the range from 1/20 to 1/5 (see Refs. [3]– [7], and [11]). In summary, the total element number of SOTS is (cn2 + 8m) at every time step. With the rapid increase of cell number n × n, it is easy to know SOTS can save 19/20– 4/5 of the elements in the two-dimensional hyperbolic– parabolic equations. By a similar analysis, we know that SOTS for the three-dimensional equations still can save 19/20– 4/5 of the elements. So one can understand why SOTS can greatly reduce the computing resources and improve the computational efficiency.
Now, we give a detailed analysis of the SOTS’ s stability. Due to the great difference of material coefficients between different kinds of materials in the composite structure, if we use the finite element method to solve problem (1) directly, the overall damping matrix and stiffness matrix are ill-conditioned matrices. Although they are all symmetric definite matrices, the difference between the maximum eigenvalue and the minimum eigenvalue of the overall damping matrix and the stiffness matrix is too big. So the numerical results will be unstable, which causes a larger error. Fortunately, if we use SOTS to solve problem (1), the overall damping matrix and the stiffness matrix have good properties because the homogenized material coefficients of homogenization problem (41) are functions which vary slowly. Therefore, the numerical algorithms we presented have good stability compared with the direct FEM. At the same time, we can use a large time step to solve homogenization problem (41) because the overall damping matrix and the stiffness matrix are both well-conditioned matrices.
Example 1 In this example, we verify our algorithms for problem (1) in which the material coefficients are all time-independent in the two-dimensional situation and we denote this case as case 1. Here Y1 represents the matrix and Y2 represents inclusions in the composite structure. Besides, we let the size ε of the periodic cell equal to 1/10. The material coefficients are

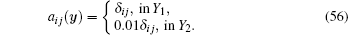
The undefined functions in problem (1) are

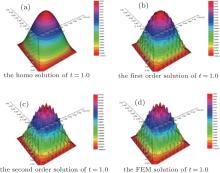
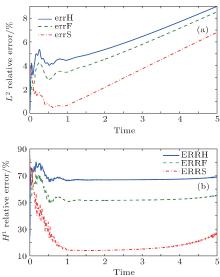
As is known to all, problem (1) does not have any analytical solution. We denote fine FEM as uε . From Table 1, it is easy to see that SOTS can greatly reduce the computational time. Figures 3 and 4 show the numerical results of u(0), u(1ε ), u(2ε ), and uε at time t = 1.0 and t = 3.0, respectively. From Figs. 3 and 4, one can find that only SOTS can accurately capture the micro-scale oscillating information and FOTS is far from enough to obtain the high accuracy solution. In Fig. 5, the damping decay behavior of point (0.45, 0.45) is shown. One can clearly see that SOTS and uε fit perfectly. Figure 6 shows that whether it is the L2 norm or the H1 norm, the accuracy of SOTS is much better than FOTS and the homogenized solution. Especially for the H1 norm, SOTS has more advantages. In practical engineering applications, engineers are more concerned about the gradient of uε because the gradient represents the flux or strain.
| Table 1. Comparison of computational cost (Δ t = 0.005, t ∈ [0, 5]). |
Remark 4 From Figs. 5 and 6, one can see that there is a bigger difference between the solution of SOTS and the fine FEM in a very short time at the beginning of the calculation. This phenomenon is because SOTS is used to capture the micro-scale fluctuation information due to the heterogeneities, but in fact the exact solutions of problem (1) do not have severe fluctuations due to the damping at the beginning. This situation is easy to handle. For example, we can use FOTS to replace SOTS or abandon the term 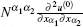
Remark 5 Notably, we use a small time step Δ t = 0.005 in the above calculation. This is only for the computational stability of the fine FEM which is needed in the error analysis. In fact, our second-order two-scale algorithm can take a large time step in practical computations and still be stable.
Example 2 In this example, we verify our algorithms for problem (1) in which the material coefficients are all time-dependent in the two-dimensional situation and we denote this case as case 2. The definitions of Y1, Y2, and ε are the same as those in example 1. The material coefficients are
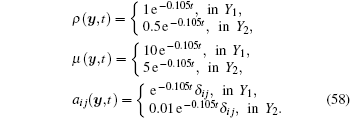
The undefined functions in equations (1) are
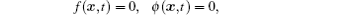
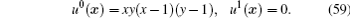
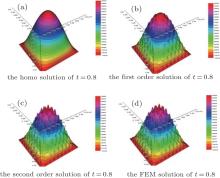
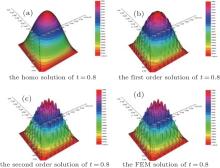
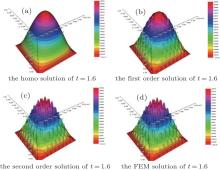
From Table 2, it is easy to see that SOTS still can greatly reduce the computational time. Figures 8 and 9 show the numerical results at time t = 0.8 and t = 1.6. From these two figures, one can find that only SOTS can accurately capture the oscillating information in the micro scale and FOTS cannot obtain the high accuracy solution of multiscale problem (1). In Fig. 10(a), the dynamic homogenized coefficient â 11(t) is shown. One can find that homogenized coefficient â 11(t) falls between the upper bound and the lower bound of the Hashin– Shtrikman bounds and the three-point bounds at every time step. Figure 10(b) shows that the accuracy of SOTS is much better than FOTS and the homogenized solution in the H1 norm sense.
| Table 2. Comparison of computational cost (Δ t = 0.002, t ∈ [0, 2]). |
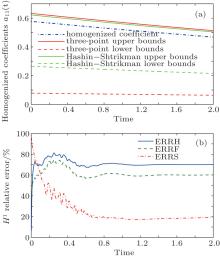 | Fig. 10. (a) â 11(t) and (b) H1 relative error of case 2. |
We discuss the second-order two-scale analysis and multiscale numerical algorithms for the hyperbolic– parabolic equations with rapidly oscillating coefficients. The new contributions of this paper include the second-order two-scale analysis, the determination of the SOTS’ s convergence rate under some assumptions, and the corresponding second-order two-scale numerical method. Numerical experiments show that the multiscale numerical algorithm we proposed is stable and efficient. Furthermore, the numerical results show that only SOTS can accurately capture the micro-scale oscillating information of multiscale problem (1).
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|