Delay systems and especially their asymptotic stability have been widely studied for several decades.^{[1– 5]} Study of the delay phenomenon is motivated by its applied aspect. Indeed, many processes include dead-time phenomena in their dynamics such as manufacturing system, turbojet engine, telecommunication, economic system, and chemical engineering system.^[6] It is generally regarded as a source of instability and poor performance which often appears in many dynamic systems, for example, chemical systems, metallurgical processing systems, nuclear reactors, long-transmission lines in pneumatic, hydraulic systems, and electrical networks.^[7] Stability analysis of dynamic systems with time delay is thus the focus of theoretical and practical importance, with many researchers recently paying heed to delay-dependent^[8] stability criteria, generally less conservative than delay-independent ones.^[9] In practice, systems almost always present uncertainty, since it is very difficult to obtain an exact mathematical model due to environmental noise, uncertain or slowly varying parameters, etc. Considerable efforts have been devoted to stability for uncertain time-delay systems.^{[10, 11]}

In recent years, the following basic mathematical model has been widely studied:^{[12, 13]}

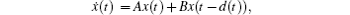
where d(t) is a time delay in the state x(t), meeting the condition 0 ≤ d(t) ≤ d and ḋ (t) ≤ μ . In Ref.  [14], the author proposed a new mathematical model with multiple additive time delays, which relates to the practical situation in a networked control system in the following form:

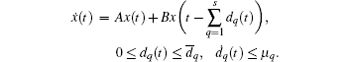
This model contains multiple delay components in the state. In Refs.  [15] and [16], the authors analyzed the stability of systems with two successive delay components,

Two additive time-varying delay models have a strapping application background in a remote control and control system.^{[17, 18]} For example, we consider a state-feedback networked control, where the physical plant, controller, sensor, and actuator are placed at different places and signals are transmitted from one device to another. Along with the delays, there are two network-induced ones, one from the sensor to the controller, and the other from the controller to the actuator. Then, the closed loop system will appear with two additive time delays in the state. Thus, in the network transmission settings, the two delays are usually time-varying with dissimilar properties. Therefore, it is of great importance to study the stability of systems with two additive time-varying delay components.^{[19, 20]}

In practice, the interest in stability analysis of various delay differential systems has been growing rapidly due to their successful applications in practical fields, such as circuit theory, chemical processes, population dynamics, distributed networks, manual control, and so on.^[21] The control design for uncertain systems with two additive time-varying delays has been a hard problem of control theory. Theoretically, the controller could be solved by the LKF approach. H_∞ performance is usually analyzed in control theory to synthesize controllers achieving stabilization with guaranteed performance. To use H_∞ methods, a control designer expresses the control problem as a mathematical optimization problem and then finds the controller that solves this optimization. H_∞ techniques have the advantage over classical control techniques in that they are readily applicable to problems involving multivariate systems with cross-coupling between channels. Thus, the problem of delay-dependent stability analysis and H_∞ control for delayed systems has received substantial observation among the control community for the past few decades.^{[22, 23]}

The H_∞ control theory considers the worst case of external disturbances to design an optimal controller to achieve the desired performance. More recently, H_∞ control theory has also been applied to an actual building in Tokyo, Japan using a pair of mass dampers to reduce the bending-torsion motion due to earthquakes.^[24] Furthermore, a liquid mono propellant rocket motor with a pressure feeding system has been considered as a numerical design example in Ref.  [25] and [26]. In Ref.  [27], the problem of controlling the yaw angles of a satellite system with delays has been discussed. This satellite system consisting of two rigid bodies joined by a flexible link is assumed to have the state-space representations. However, H_∞ control synthesis for systems with two additive time-varying delays has not been considered yet. This motivates this study.

From the above discussion, we establish a new LMI condition by using the LKF with triple integral terms and applying the Lemma in Ref.  [28] together with the zero function to guarantee the asymptotic stability of the system. A sufficient condition for the solvability of this problem is proposed in terms of LMI and the expression of desired controllers is given. Particularly, the minimal allowable length of H_∞ performance is obtained from LMI and the validity of this result is checked numerically using the effective LMI control toolbox in Matlab.^[29] The results are also compared with existing methods.

Notations Throughout this paper, ℜ ⁿ and ℜ ^{n× n} denote, respectively, the n-dimensional Euclidean space and the set of all n × n real matrices. For a matrix B and two symmetric matrices A and C, denote the symmetric matrix, where the notation * represents the entries implied by symmetry. The A^T and A^{− 1} denotes the matrix transpose and inverse of A, respectively. We say X > 0 means that the matrix X is real symmetric positive definite with appropriate dimensions. I denotes the identity matrix with appropriate dimensions. Let , f (t) ∈ L₂[0, ∞ ) ∥ f∥ refer to the Euclidean norm of the function f(t) at time t. L₂[0, ∞ ) is the space of square integrable vectors in [0, ∞ ).

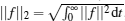
Consider an uncertain system with two additive time-varying delays of the form,

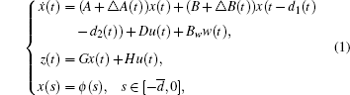
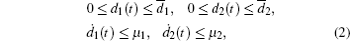
where x(t) ∈ ℜ ⁿ and x(t) is the state at time t defined by x_t(θ ) : = x(t + θ ), ∀ θ ∈ [− d, 0], u(t) ∈ ℜ ^m is the control input, and w(t) ∈ ℜ ^p is the disturbance input which belongs to L₂[0, ∞ ). z(t) ∈ ℜ ^q is the controlled output of the system. The initial vector ϕ ∈ C₀, where C₀ is the set of continuous functions from [− d, 0] to ℜ ⁿ. d₁(t) and d₂(t) denote the time-varying delays, and are assumed to satisfy

where d₁, d₂, μ ₁ and μ ₂ are positive constants. We denote

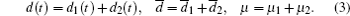
The matrices A, B, D, B_w, G, and H are known real constant matrices with appropriate dimensions. Δ A(t) and Δ B(t) are real-valued unknown matrices representing time-varying parameter uncertainties, and are assumed to be of the form

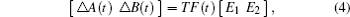
where T and E_j (j = 1, 2) are known real constant matrices, and F(t) is unknown time-varying matrix functions satisfying

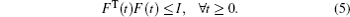
Lemma 2.1^[28] Let M, P, and Q be given matrices such that Q > 0, then

Lemma 2.2^[30] For any constant matrix Z ∈ R^{n× n}, Z = Z^T > 0, scalars h₂ > h₁ > 0, such that the following integrations concerned are well defined:

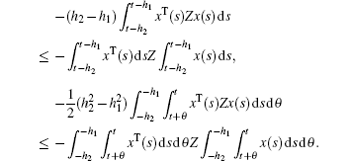
Lemma 2.3^[31] Ξ ₁, Ξ ₂, and Ω are constant matrices of appropriate dimensions and 0 ≤ d₁ ≤ d(t) ≤ d₂, then

if and only if

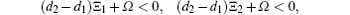
hold.

Lemma 2.4^[32] Let D, E, and F(t) be real matrices of appropriate dimensions, and F(t) satisfy F^T(t)F(t) ≤ I. Then, the following inequality holds for any constant ε > 0:

Lemma 2.5^[33] Let T > 0, any appropriate dimension S and 0 ≤ d(t) ≤ d, then

holds.

In this section, we derive a new delay-dependent criterion for the system  (1) without uncertainties (Δ A(t) = Δ B(t) = 0) using the LKF method combining with LMI technique. System  (1) can be written as follows:

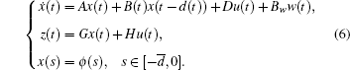
Firstly, we establish a new delay-dependent stability criterion for the system  (6) with u(t) ≡ 0.

Theorem 3.1 For a prescribed scalar γ > 0 and some given scalars d₁ > 0, d₂ > 0, μ ₁ > 0, and μ ₂ > 0, the system described in Eq.  (6) with u(t) ≡ 0 is asymptotically stable and satisfies ∥ z(t)∥ ₂ ≤ γ ∥ w(t)∥ ₂ for all nonzero w(t) ∈ L₂[0, ∞ ) if there exist matrices P₁₁ > 0, R₁₁ > 0, R₁₂, R₂₂ > 0, Q_r > 0 (r = 1, … , 6), Z_s > 0 (s = 1, … , 7) and appropriately dimensioned matrices W, N_i, M_i, L_i, S_i, V_i (i = 1, … , 10), such that the following LMI is satisfied:

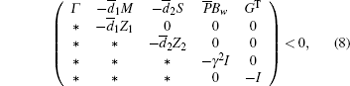
where

with

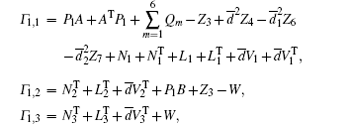
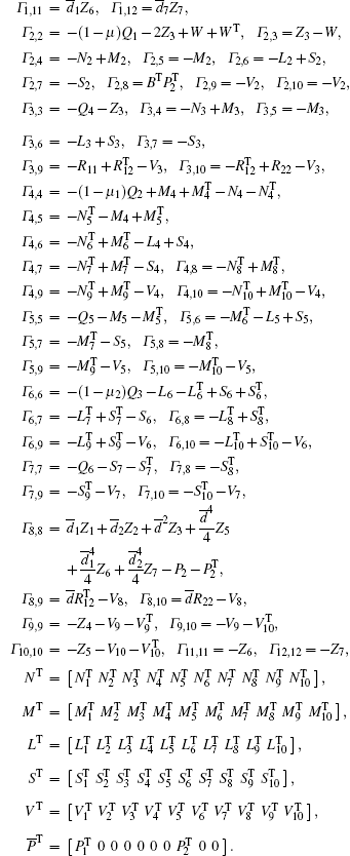
Proof Define the Lyapunov functional candidate as

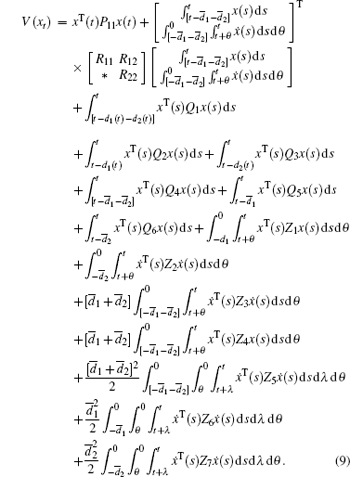
The time derivative of V (x_t) is given by

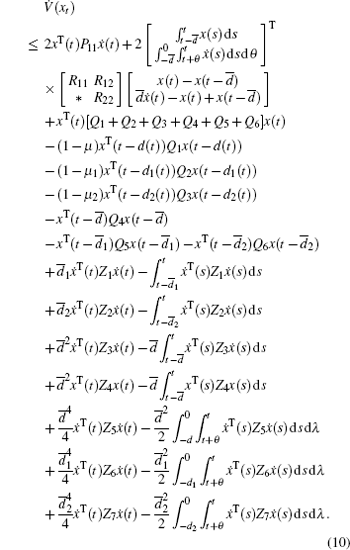
By using Lemma 2.3, the above equation can be written as

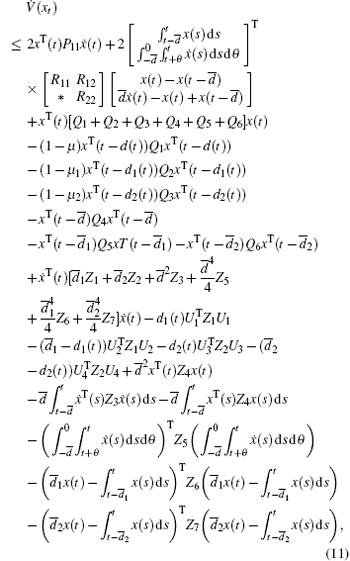
where

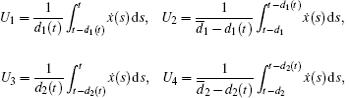
and

Based on Lemma 2.5, we have

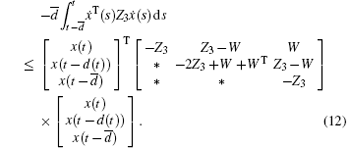
From Leibniz– Newton' s formula, the following equations are true for any matrices N, M, L, S, V, P with appropriate dimensions:

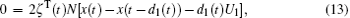
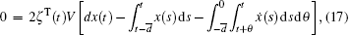
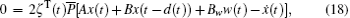
where

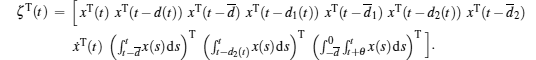
Combining Eqs.  (10)– (18), we obtain

where

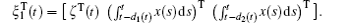
We can write V̇ (x_t) as

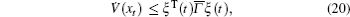
where

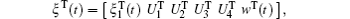
and

Note that

where

Under the zero initial conditions for the system (1), we have

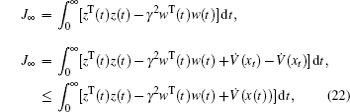
where V (x_t) is given by Eq.  (9). By substituting Eq.  (21) into Eq.  (22), we have

where

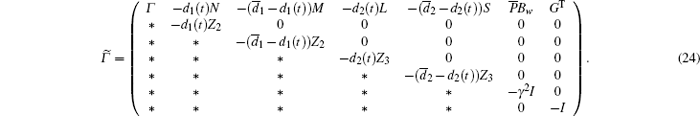
By using Lemma 2.3, we know that equation  (24) is equivalent to Eqs.  (7) and (8). Now it is easy to see that ∥ z∥ ₂ ≤ γ ∥ w∥ ₂, for any nonzero w(t) ∈ L₂[0, ∞ ) is satisfied.

Theorem 3.2 For a prescribed scalar γ > 0 and some given scalars d₁ > 0, d₂ > 0, μ ₁ > 0, and μ ₂ > 0, the system described in Eq.  (1) with u(t) ≡ 0 is asymptotically stable and satisfies ∥ z(t)∥ ₂ ≤ γ ∥ w(t)∥ ₂ for all nonzero w(t) ∈ L₂[0, ∞ ) if there exist matrices P₁₁ > 0, R₁₁ > 0, R₁₂, R₂₂ > 0, Q_r > 0 (r = 1, … , 6) Z_s > 0, (s = 1, … , 7), and appropriately dimensioned matrices W, N_i, M_i, L_i, S_i, V_i (i = 1, … , 10), and a scalar ε > 0 such that the following LMI is satisfied:

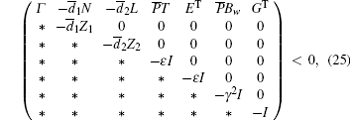
where

Proof Replace A and B in Γ ̃ by A + Δ A(t) and B + Δ A(t), respectively, we obtain

From Lemma 2.4 we know that equation  (27) is equivalent to

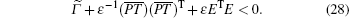
Obviously, by using the Schur complement Lemma and Lemma 2.3, we obtain Eqs.  (25) and (26).

Remark 3.1 It should be noted that, when deriving an upper bound of the time derivative of V (x_t) in Eq.  (9) it includes not only single integral terms of states but also triple integral terms of states. In stability analysis of uncertain systems with two additive time-varying delays, this consideration has not been utilized in previous results.^[21] Thus, more information on states can be utilized in the criterion presented in Theorem 3.1.

In this section, we present a delay-dependent H_∞ sufficient condition for the system  (1). Using the state feedback controller u(t) = Kx(t), the following theorem is derived by extending Theorem 3.2. That is, u(t) ≠ 0.

Theorem 4.1 For a prescribed scalar γ > 0 and some given scalars d₁ > 0, d₂ > 0, μ ₁ > 0, μ ₂ > 0, and a > 0, the system described by Eq.  (1) is asymptotically stable and satisfies ∥ z(t)∥ ₂ ≤ γ ∥ w(t)∥ ₂ for all nonzero w(t) ∈ L₂[0, ∞ ) if there exist matrices , X > 0, Y, and appropriately dimensioned matrices , and a scalar ε > 0 such that the following LMI is satisfied:

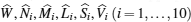
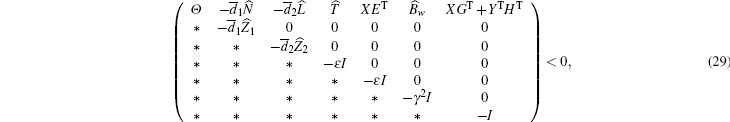
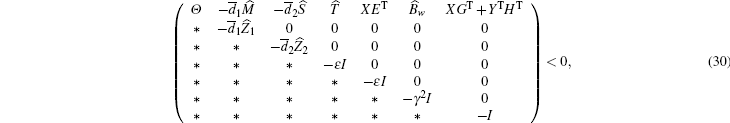
where

with

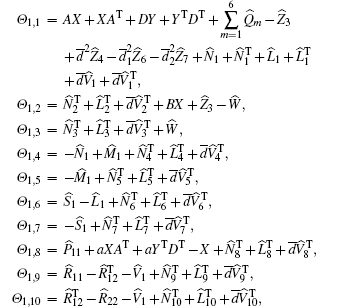
and the feedback gain matrix is given by K = YX^{− 1}.

Proof Now we define P₁ = P, P₂ = a₂P, and P₃ = a₃P, where P is a nonsingular matrix and a_i > 0 (i = 2, 3). Furthermore, we define

Then pre and post multiplying LMIs  (25) and (26) by diag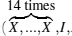 and its transpose, respectively, we can obtain Eqs.  (29) and (30).

Remark 4.1 In order to show the lesser conservatism of our stability criteria, we consider the following system, as a special case of the system  (1).

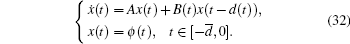
Corollary 4.1 For some given scalars d₁ > 0, d₂ > 0, μ ₁ > 0, and μ ₂ > 0, the system described in  (32) is asymptotically stable if there exist matrices P₁₁ > 0, R₁₁ > 0, R₁₂, R₂₂ > 0, Q_r > 0 (r = 1, … , 6), Z_s > 0 (s = 1, … , 7) and appropriately dimensioned matrices W, N_i, M_i, L_i, S_i, V_i (i = 1, … , 10), such that the following LMI is satisfied:

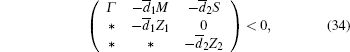
where Γ , N, M, L, and S are the same as defined in Theorem 3.1. The proof of the above corollary is the same as that in the proof of Theorem 3.1. Hence it is omitted.

Remark 4.2 In this paper, we contribute to the improvement of the robust stability analysis of delay-dependent H_∞ control of uncertain systems with additive time-varying delays which lies in the above results. First, new robust stabilization criteria were established on the basis of a novel LKFs with triple integral terms for additive time-varying delays. Second, by introducing free-weighting matrices and using a convex combination technique, sufficient conditions (robust H_∞ control) are derived for the considered uncertain system in terms of LMIs, which can be easily calculated by using Matlab LMI control toolbox.

Remark 4.3 From Corollary 4.1, we can obtain the delay bounds d₁ or d₂ when the other is known through solving the following convex problem:

In this section, some numerical examples are provided to demonstrate that the proposed method in this paper is effective and less conservative than the existing methods.

Example 1 Consider the uncertain system (1) with the following matrix parameters:

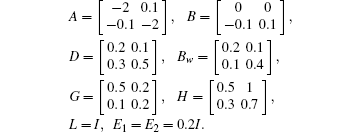
In order to design a delay-dependent H_∞ controller, taking u₁ = 0.4, u₂ = 0.5, d₁ = 1.5, d₂ = 1.5, and a = 0.2, applying the Theorem 4.1 in Matlab LMI Toolbox, the feasible solutions are

Based on Theorem 4.1, we can obtain the desired state feedback controller as follows:

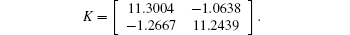
Therefore, the concerned system is asymptotically stable.

Example 2 Consider the following system with matrix parameters in Ref.  [16]:

with

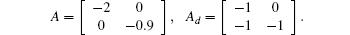
When μ ₁ = 0.1 and μ ₂ = 0.8, by solving Example 2 using LMI in Corollary 4.1, we obtain the delay bounds in different cases. The admissible maximum allowable delay bound d₂ and d₁ are listed in Tables  1 and 2, respectively. This indicates that the results obtained in this paper are significantly better than those in Refs.  [16]– [21].

Table 1.

Table 1.

Table 1. Example 2. Delay bounds d2 for given d1. Methods d1 = 1 d1 = 1.1 d1 = 1.2 d1 = 1.5 Corollary 4.1 3.751 3.651 3.551 3.251 Theorem 1[21] 1.416 1.316 1.216 0.916 Proposition 2[20] 0.873 – 0.673 0.373 Theorem 1[19] 0.872 0.772 0.672 0.372 Theorem 1[18] 0.596 – 0.463 0.313 Theorem 2[17] 0.583 – 0.519 0.421 Theorem 1[16] 0.519 0.486 0.453 0.378

Table 1. Example 2. Delay bounds d2 for given d1.

Table 2.

Table 2.

Table 2. Delay bounds d1 for given d2. Methods d2 = 0.1 d2 = 0.2 d2 = 0.3 d2 = 0.4 d2 = 0.5 Corollary 4.1 4.652 4.552 4.452 4.352 4.252 Theorem 1[21] – – 2.116 2.106 1.916 Theorem 2[17] 2.998 2.332 1.900 1.473 1.373 Proposition 2[20] – – 1.573 1.473 1.373 Theorem 1[19] – – 1.572 1.472 1.372 Theorem 1[16] 2.918 2.330 1.833 1.413 1.060 Theorem 1[18] 2.340 1.834 1.532 1.313 1.140

Table 2. Delay bounds d1 for given d2.

In this work, we have studied the robust H_∞ control of uncertain systems with two additive time-varying delays. On the basis of the Lyapunov method, a delay-dependent H_∞ control scheme is presented in terms of linear matrix inequalities. It has been shown that a desired state feedback controller can be constructed when the given linear matrix inequalities are feasible. Some numerical examples have shown that our results are less conservative than existing methods. We would like to point out that it is possible to extend our main results to a more general H_∞ control for uncertain stochastic systems with two additive time-varying delays. The results will be obtained soon.