The terahertz (THz) range of the electromagnetic spectrum serves as a bridge between the world of traditional electronics and optics. However, scientific hurdles, such as effectively generating and detecting THz wave, restrict its applications. Consequently, many scientists and engineers have made efforts to solve these two issues in past decades.^{[1– 7]} For THz generation, thanks to the advent of ultrashort laser pulse with millijoule energy, single-cycle electromagnetic radiation covering THz gap (0.1  THz– 10  THz) with MV/cm electric field amplitude can be generated from laser-induced gas plasma.^{[8– 11]}

Generation of THz radiation from gas plasma scheme was first demonstrated by Hamster et al.^{[12, 13]} One single frequency femtosecond (fs) laser beam is focused in the air to ionize the gas, and conical THz emission can be detected at an angle with respect to the direction of propagation. The underlying mechanism was explained as ponderomotive acceleration of the ionized electrons in the plasma.^[13] Since then, other gas-plasma THz generation schemes, such as the “ DC-bias” method^[14] and the “ AC-bias” method, ^[15] have been demonstrated. In particular, the “ AC-bias” method, also known as ω – 2ω scheme or two-color scheme, can significantly improve THz generation efficiency. Its physical mechanism was initially treated as a four-wave mixing (FWM) process.^[16] However, this nonlinear model failed to explain some subsequently measured results, e.g. saturation of THz output.^{[15, 16, 17]} Kim et al. developed a so-called transient photocurrent (PC) model, which claimed that coherent THz waves originated from a net electron current surge generated by an asymmetric two-color laser field.^{[18– 21]}

According to the PC model, the asymmetry of two-color field leads to the asymmetric ionization of bound electrons and asymmetric acceleration process of ionized electrons, during which ultra-broadband THz wave with high E-field amplitude is radiated. Based on this, stronger THz radiation should be expected if the symmetry of the total field is further broken by adding more color laser fields. In this paper, we theoretically investigate the generation of THz waves from the gas-plasma induced by tri-color ultrashort laser fields. The transient photocurrent model of three-color mixing field is used, and we obtain enhancement, suppression, and polarity modulation of THz radiation by adjusting the relative phase between 3ω and ω field, with the relative phase between 2ω and ω fields fixed to be a certain value. We clearly reveal how the 3ω laser pulse affects the non-vanishing net electronic current surge by analyzing the ionization process in one optical period. The simulation results show that the relative phase between 3ω and ω fields plays a key role in the generation process, which offers a way to control the generation of THz radiation from the gas plasma, such as the intensity and polarity of THz waves.

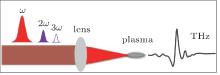
Generation of THz wave from gas plasma induced by tri-color ultrashort laser pulses is sketched in Fig.  1. Three fs-laser pulses (ω + 2ω + 3ω ) are synchronally and collinearly focused to ionize the gas, from which radiates an electromagnetic wave (including THz wave band).

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Schematic diagram of a tri-color mixing THz wave generation.

Let the energy of the fundamental light (800  nm) be J₁, the field amplitude can be expressed as

where c is the speed of light in vacuum, ε ₀ is the permittivity in air, w₀ = 10  μ m represents radius of 1/e²-beam waist, T₁ is the pulse duration (relative to the full width at half maximum (FWHM) width via , T_FWHM = 30  fs). Assume a Gaussian envelope, the electric field of the ω pulse can be written as^[10]

Similarly, the electric fields of 2ω and 3ω can be written as

Here, θ ₂ is the relative phase between 2ω and ω fields, and θ ₃ is the relative phase between 3ω and ω fields. The total laser field is the superposition of the three fields and is expressed as

Supposing the ionization to be a static tunneling (ST) process, ^{[10, 22– 25]} one can write the ionization rate in the form of

where is the electric field in atomic units (E_a = 5.14× 10¹¹  V/m), , is atomic frequency unit, r_H is the ionization potential of the target molecules relative to that of hydrogen by Here we assume that the gas is composed of neutral nitrogen molecules with , and the initial gas molecule density is N_g = 2.4× 10²⁵  m ^{− 3} (under standard pressure). The evolution of the generated electron density N_e(t) at moment t can be derived from the rate equation^[10]

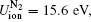
Once the bound electrons of nitrogen molecules are stripped off by the laser field, their ensuing movement can be described with classical mechanics. The ionized electrons will be accelerated by an external laser field at an acceleration of

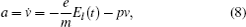
where e and m are the electron charge and mass, respectively, − pv represents attenuation item caused by electron– ion collision with scattering time 1/p. In our case, the laser pulse duration (∼ 30  fs) is much shorter than the scattering time (∼ 1  ps), ^[24] thus − pv item can be ignored and the acceleration is then simplified into v̇ = − eE_l(t)/m. Assuming that the ionized electrons are at rest at the ionization instant t₀, the velocity at a subsequent time t is

The transverse electronic current density at time t can be calculated from

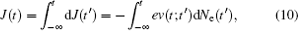
where dN_e(t′ ) denotes the increment of electron density in the interval between time t′ and t′ + dt′ , v(t; t′ ) is the velocity of those electrons at t. This current surge gives rise to electromagnetic radiation, covering the THz wave band. The electrical field of the radiation is proportional to rate of change of the current density as E_T ∝ dJ/dt. The spectrum is obtained from a Fourier transform of dJ/dt, the time domain waveform is achieved after filtering and inverse Fourier transformation.

The dependence of ionized electron density on pulse energy is first depicted in Fig.  2, in which the red and blue lines represent the results obtained from tri-color and two-color schemes, respectively. Note that the N₂ molecule is ionized up to with the characteristic stepwise ionization twice per laser cycle.^{[18, 24, 25]} Points A (A′ ), B (B′ ), C (C′ ), D (D′ ), and E (E′ ) correspond to five typical status: threshold point, inflection of the primary ionization, saturation of the primary ionization, inflection of the secondary ionization, and saturation of the secondary ionization, respectively. From these points, it is clearly seen that the tri-color scheme needs lower energy than two-color scheme for the same state because the symmetry of the total field is further broken in the former scheme. Since the generation of THz wave mainly corresponds to the first saturation, the laser energy in the following calculations is fixed to be no more than J₁ = 14.05  μ J.

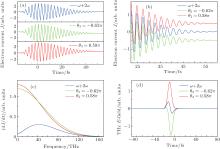
For a two-color scheme, the THz yield is strongly phase-dependent. The THz radiation is strongest at θ ₂ = 0.5π and weakest at θ ₂ = 0, ^{[18, 20, 21]} which, according to the PC model, means that the symmetry of laser field has a largest break at θ ₂ = 0.5π and a smallest break at θ ₂ = 0. Therefore, we set the values of θ ₂ to these two values and set the value of θ ₃ to be varying in a 2π period to study its influence. Figure  3 illustrates the dependences of THz field on θ ₃ in tri-color scheme. Here, the energy ratio of 2ω pulse to ω pulse and that of 3ω pulse to ω pulse are fixed to be 0.2 and 0.05, respectively, assuming that their corresponding conversion efficiencies are 20% and 5%.^{[20, 26]}

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Plots of maximum electron density versus pulse energy, where points A (A′ ), B (B′ ), C (C′ ), D (D′ ), and E (E′ ) represent threshold point, inflection of the first ionization, saturation of the first ionization, inflection of the secondary ionization and saturation of the secondary ionization, respectively.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. ((a), (b), (d), and (e)) Maximum THz yields versus relative phase θ 3, and ((c) and (f)) comparisons between the increment of THz radiation and that of the two-color scheme.

As shown in Figs.  3(a) and 3(b), the THz field and energy have maximums at θ ₃ = − π or π when θ ₂ = 0.5π , respectively. Figure  3(c) gives the increment of THz electrical field and energy, which are compared with those of two-color scheme, are 75% and 180%, respectively. Whereas the minimums are obtained at θ ₃ = 0, with electric field decreasing 40% and energy decreasing 80%, respectively. However, the situation is a little different when θ ₂ = 0. The maximums of THz field appear at around θ ₃ = ± 0.6π and its minimums are at around θ ₃ = 0 (or ± π ). Besides, the polarity of the electric field as shown in Fig.  3(d) is suddenly reversed at θ ₃ = − 0.04π , which does not appear when θ ₂ = 0.5π . THz energy reaches the maximums at θ ₃ = − 0.65π and 0.63π , with increments of about 1200% and 1300% compared with those of two-color scheme.

From the above results, one can conclude that the THz emission can be affected by adding a 3ω field, and modulated with relative phase θ ₃. Note that although higher intensity of THz yield is acquired for θ ₂ = 0.5π , the modulation of THz wave is weaker. While for θ ₂ = 0, larger modulation capacity is expected, and even the polarity of THz electrical field can be reversed by changing the relative phase θ ₃.

To further understand the above enhancement, suppression, and reversed polarity of THz radiation phenomena, we perform the following calculations.

The evolutions of total laser field (including three cases: (i)ω + 2ω field (base case), (ii)θ ₃ = 0 (maximum inhibition) and (iii)θ ₃ = π (maximum enhancement)) and electron density with time are illustrated in Fig.  4(a). As can be seen, the increment of electron density mainly occurs in a time range from − 15  fs to 0  fs, which are zoomed and illustrated in Figs.  4(b)– 4(d).

Fig.  4.

	Figure Option ViewDownloadNew Window
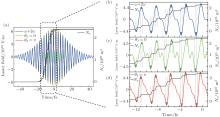	Fig.  4. Laser electric field and electron density versus time in case (i)(blue line), case (ii)(green line), and case (iii)(red line).(a):Overall trend. (b)– (d): Zoomed portion of graph (a).

The ionization process, corresponding to the increment of electron density, mainly takes place in the areas between the dotted lines in Figs.  4(b)– 4(d). According to the former analysis, the reason why the mixed two-color field enhances THz radiation lies in the fact that the symmetry of ω -field is broken by adding the introduced 2ω -field. The acceleration time of ionized electrons in the first half laser cycle is different from that in the second half cycle. Thus, the macroscopic electronic currents along the two directions of laser polarity cannot be offset and tends to cumulatively increase along one direction, finally forming a non-zero electron current surge, which gives rise to terahertz emission. The larger the current surge, the stronger the THz radiation is, just like what equation  (10) indicates. For the tri-color scheme, the third harmonic field will further change the symmetry of the total laser field at different relative phases, and bring about different results for THz generation.

Figure  5(a) shows the variations of the electronic currents of the above three cases with time, and figure  5(b) display their zoomed portions. As can be seen, the ultimate current surges for the three cases are in a order of case (iii) > case (i) > case (ii), which is in accordance with the relations among strengths of spectra and among the waveforms of the three cases depicted in Figs.  5(c) and 5(d), respectively. This result satisfies our theory and can be roughly explained below.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. (a) Time-varying electronic currents produced by plasma in case (i) (without 3ω pulse, blue line), case (ii) (θ 3 = 0, green line), and case (iii) (θ 3 = π , red line). (b) Zoomed portions of curves in panel (a). (c) Time-varying spectra of the three cases. (d) Time-varying THz waveforms of the three cases.

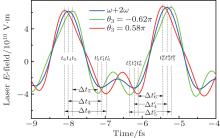
We elaborate the above result in the aspects of photoionization and acceleration process. Figure  6 shows the total laser fields in one cycle (in a time range from about − 10  fs to − 6  fs) for three cases, respectively. The t₁, t₂, and t₃ represent the instants of the first time ionization in one optical period under circumstances of 2ω field (case (i), blue line), θ ₃ = 0 (case (ii), green line), and θ ₃ = π (case (iii), red line), respectively. The , and represent the second time ionization instant, respectively. The , , and are the first time ionization instant in next period. Therefore, represents the acceleration time of ionized electrons in the first time ionization in case (i) (case (ii)/case (iii)). While denotes acceleration time of ionized electrons in the second time ionization in case (i) (case (ii)/case (iii)). It is obvious from Fig.  6 that , i.e., the difference in acceleration time between the two ionized electrons obeys such a relationship: case (ii) < case (i) < case (iii). Thus, the net current after offsetting for three cases in one optical cycle obeys the same situation. Within each cycle in which the photoionization occurs, the net currents after offsetting all behave in the same manner, therefore the ultimate non-zero electron current as well as the terahertz yield from it, all follow the same relation of case (ii) < case (i) < case (iii), as evidenced in Figs.  5(a)– 5(d). In other words, a 3ω field with θ ₃ = π brings the largest asymmetry to the total field, while a 3ω field with θ ₃ = 0 cancels for the most effect (compared with the ω – 2ω case). As a result, terahertz emission with disparity substantial in strength are obtained, as the PC model predicts.

Fig.  6.

	Figure Option ViewDownloadNew Window
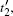
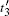
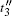
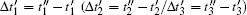
	Fig.  6. Laser electric fields versus time in one cycle of case (ii) (blue line), case (ii) (green line), and case (iii) (red line).

From Figs.  5(c) and 5(d), it is clear that introduction of a 3ω field can affect the radiation intensity but not the width of the spectrum. Another point that should be noted is, with θ ₂ = 0.5π the polarities of THz waveforms are all along the same direction for the three cases. Namely, the capability of controlling THz polarity is missing for θ ₂ = 0.5π . The reason for the absence may be as follows. According to the PC model, it is the asymmetry of the laser field that results in effective THz emission. This is why a single frequency fs-laser (with long pulse duration) could not achieve the terahertz generation but a few-cycle laser could. With θ ₂ = 0.5π , the symmetry of the total field is broken so hard that the addition of a 3ω pulse can only enhance or suppress this trend to some extent but cannot change it radically. However, for θ ₂ = 0, the ω – 2ω field itself is symmetrical, and is ready to be changed along different directions by adding a 3ω pulse with different relative phases. Therefore, although THz radiation is relatively weak, large modulation ability should be expected for θ ₂ = 0, which is clearly seen from Fig.  3 and will be discussed in detail in the next subsection.

Figures  7(a)– 7(d) show the evolutions of the laser field and electron density with time in three cases: (iv) 2ω field (base case), (v) θ ₃ = − 0.62π (maximum inhibition), and (vi) θ ₃ = 0.58π (maximum enhancement), respectively.

Fig.  7.

	Figure Option ViewDownloadNew Window
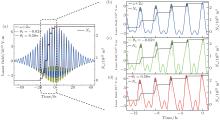	Fig.  7. Laser electric fields and electron densities versus time in case (iv) (blue line), (v) (green line), and (vi) (red line). (a): Overall trend. (b)– (d): Zoomed portion of curves in panel (a).

Figure  8(a) shows the time evolutions of electron current for the above three cases, and figures  8(c) and 8(d) display the spectrum and time domain waveforms, respectively. As can be seen from Fig.  8(d), the THz fields in the cases (v) and (vi), with opposite polarities, are much larger in strength than that in case (iv). The same trend is shown in Fig.  8(b), in which ultimate current surge is plotted. The reason for this is similar to earlier analysis, and can be roughly described as follows.

Fig.  8.

	Figure Option ViewDownloadNew Window
	Fig.  8. (a) Time-varying electron current produced by plasma in the case (iv) (without 3ω pulse, blue line), case (v) (θ 3 = − 0.62π , green line), and case (vi) (θ 3 = 0.58π , red line). (b) Zoomed portions of curves in panel (a). (c) Spectra of the three cases. (d) THz waveforms of the three cases.

Figure  9 shows the laser fields in one cycle (in a time range from about − 9  fs to − 4  fs) for the three cases, respectively. For case (iv) (only ω + 2ω scheme, blue line), the total field is an even function since both the ω field and 2ω field are even (see Eqs.  (2)– (5)). Therefore, the time interval from peak to valley equals that from valley to peak during which the effect of electron acceleration largely offsets and results in a near-zero net current and weak THz emission.^{[18– 20]} As for θ ₃ = 0.58π (case (vi), red line) and θ ₃ = − 0.62π (case (v), green line), the symmetry of the electric field is broken along different directions: acceleration time for case (v) is longer than in one cycle, while opposite for case (vi) , . So the net currents accumulated in the photoionization process for cases (v) and (vi) as shown in Figs.  8(a) and 8(b), are both non-zero, leading to a strong THz wave compared with that in case (iv). It is worth noting that since the accumulated net currents for cases (v) and (vi) are along the opposite directions, THz waves with opposite polarities are obtained, as shown in Fig.  8(d).

Fig.  9.

	Figure Option ViewDownloadNew Window
	Fig.  9. Laser electric fields versus time in one cycle of case (iv) (blue line), case (v) (green line), and case (vi) (red line).

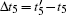
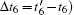
In this work we theoretically studied the THz generation from gas plasma induced by tri-color ultrashort laser pulses. Numerical calculations show that the relative phase θ ₃ between 3ω and ω plays a key role in this process; that is, THz generation is phase-dependent and can be modulated by varying θ ₃. In addition, we provide a simple but clear perspective to understand this effect from point view of photoionization process. It should be noted that the above discussion is on condition that the energy ratio between contributing pulses are fixed to a certain value. Besides, macroscopic effects, such as laser pulse propagation, dispersion, and absorption of THz in air and plasma are not included in this model, and will be considered theoretically and experimentally for further discussion.