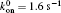Focal adhesions are discrete adhesive sites existing between cell and its extracellular matrix. These adhesive plagues are multi-protein complexes, comprised of almost 200 different proteins.^[1] Each complex is connected to a stress fiber inside the cell and also coupled to the extracellular matrix through a layer of transmembrane receptors, which are mainly of integrins. Since the connected stress fibers are contractile, pulling forces on focal adhesions are generally generated.^[2] Indeed, focal adhesions are force-responsive, which can grow with forces and shrink without forces.^{[3– 5]} A mature focal adhesion is often of a slender structure with a size falling about 1 μ m.^{[4, 6]} Through focal adhesions, cell actively senses and responds to the mechanical signals from its environment, including mechanical forces, stiffness, and deformation, which then regulate various cellular processes and functions.

Under physiological conditions, various cells are constantly subjected to fluctuated forces, for example, due to the pulsating heart beats. These fluctuated forces can be critical to the normal functions of these cells.^{[7, 8]} In vitro experiments it was demonstrated that cell adhered to elastic substrates reoriented themselves nearly perpendicular to the stretching direction when substrates were subjected to uniaxial cyclic stretch.^{[8– 20]} It looks as if cell tried to avoid a fatiguing load on them. The characteristic time of reorientation for fibroblasts at sub-confluent densities was quantified, which depends on both the fluctuation amplitude and the fluctuation frequency.^[11] It was shown that this characteristic time decreased with the fluctuation amplitude and the fluctuation frequency until it became saturated above 1 Hz at a fixed amplitude.^[11]

In probing the effects of fluctuated forces on the stability of focal adhesions, Chen X and Chen B^[21] directly simulated the stability of a cluster of slip bonds subjected to fluctuated forces with a coupled finite element analysis (FEA) and Monte Carlo method. The simulation results indicated that the lifetime of the bond cluster, in many cases, decreased with increasing fluctuation amplitude and also decreased with increasing fluctuation frequency, which appeared to be saturate at high fluctuation frequencies.^[21] These results were consistent with the experimental reports, suggesting the possible role of slip bonds in cellular reorientation under cyclic stretches.^[21] However, an unusual case was also reported, where a fluctuated force dramatically increased the lifetime of the bond cluster.^[21] This unusual observation occurred only when the fluctuation frequency was relatively low but the fluctuation magnitude was relatively high.^[21] We refer to the observation that the lifetime of the bond cluster substantially increases with fluctuation frequency as “ unusual stability enhancement” .

The “ unusual stability enhancement” only occurring at relatively large stretch magnitude is quite surprising and difficult to explain. For example, the system under investigation by Chen X and Chen B^[21] might bear some similarities to a fatigue test. In light of fracture theory, the lifetime of a fatigue crack would decrease with the fluctuation amplitude instead, according to the well-known Paris’ law.^[22] Thus, the prediction of fracture theory would contradict to this “ unusual stability enhancement” . Then, one may wonder whether such a phenomenon of “ unusual stability enhancement” is robust or what it depends on.

To answer these questions, here we carry out parametric studies on the “ unusual stability enhancement” of a cluster of slip bonds subjected to fluctuated forces. Our intensive simulation results indicate that the “ unusual stability enhancement” often occurs when fluctuation frequency is relatively low and fluctuation amplitude is relatively high, which, however, is affected by the stochastic features of a single bond and the profile of the fluctuated forces, such as the average value of bond force. Since it was recently found that the traction forces within a focal adhesion can coincidentally fluctuate at a frequency of about 0.1  Hz with a relatively large fluctuation amplitude, ^[6] we then suggest that the fluctuation of traction forces within a focal adhesion might enhance its stability in this way.

Following the study by Chen X and Chen B, ^[21] a focal adhesion is represented with a cluster of molecular bonds, which adheres an elastic fiber to a rigid substrate as schematically shown in Fig.  1. The stretch stiffness of the fiber is denoted as EA. The fiber is subjected to a fluctuated force along the horizontal direction on its right end, described by^[23]

where P₀ is the average force within one period, related to the homeostatic tension within a stress fiber, f is the fluctuation frequency, t is the time, and α is termed the fluctuation amplitude, ranging from 0 to 1.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. A cluster of slip bonds representing a single focal adhesion (FA) existing between a rigid substrate and a stress fiber (SF). The fiber is subjected to a fluctuated force, P(t), along the horizontal direction on the right end.

We let ligands uniformly be distributed on a portion of the substrate surface and the receptors be uniformly distributed along the fiber as shown in Fig.  1.^[21] There are N_R receptors on the fiber and N_L ligands on the substrate with N_L > N_R. The distances between neighboring receptors and ligands are the same, denoted as l₀. Initially, closed bonds are formed between all receptors and their ligands, which behave as slip bonds under forces.^[21] For a slip bond, its dissociation rate is governed by the Bell’ s law, ^[24]

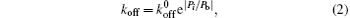
where 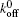is the spontaneous dissociation rate without force, P_i is the force on the i-th bond, and P_b is a force scale, typically about a few pNs.

Due to thermal fluctuation, a dissociated receptor can be rebound into a free ligand on substrate surface to form a new bond. The corresponding rebinding rate is given by^[21]

where is the reaction rate of a bond when the ligand and its receptor are within binding distance l_bind, k_LR is the spring constant of the bond, K_B is the Boltzmann constant, T is the absolute temperature, v₀ = a/τ ₀ is an intrinsic velocity, ^[25] with a being a length scale ∼ 10  nm and τ ₀ being an intrinsic association time, ranging from 0.01  s to 1  s.^{[26, 27]}

We model the elastic fiber as a one-dimensional (1D) elastic rod and also the molecular bonds as linear springs.^[21] Following the work by Chen X and Chen B, ^[21] the system is simulated with a coupled Monte Carlo method and finite element analysis. At each time step, the forces and displacement in the system at any future time are solved with finite element analysis.^[21] Next, we use the kinetic Monte Carlo method to determine where and when the next random event would occur.^[21] Let r_i denote the dissociation rate if a bond is currently closed or the rebinding rate if the bond is currently open. A series of random numbers, ξ _i, uniformly distributed between 0 and 1, are generated and the duration needed for the i-th random event to take place, τ _i, is obtained by solving^[28]

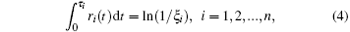
where n is the current number of possible random events. The time step for the next random event to occur, Δ t, would be the smallest one in all τ _i (i = 1, 2, ..., n), given by

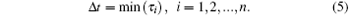
The next random event is also determined. The system is subsequently updated. The bond will be open if it is currently closed or be closed if it is currently open at the place where the random event takes place. The simulation will then proceed to the next step. The above procedure is looped until all the bonds are open or t is larger than a very large value, set to be 4000  s in the simulation. The mean lifetime of the bond cluster is obtained by running the simulation 100 times.^[21] The default values in the simulation include EA = 45.6  nN, ^[29]N_R = 40, N_L = 80, l_bind = 2  nm, and l₀ = 32  nm.^[30]

We then carry out parametric studies on the “ unusual stability enhancement” of the bond cluster under fluctuated forces. We first investigate the effects of parameters in the dissociation rate of a single slip bond in Eq.  (2), and P_b. The effects of are shown in Fig.  2. We find that increasing generally reduces the lifetime of the cluster. As seen in Fig.  2(a), when and α = 1, there may exist the “ unusual stability enhancement” . When , the “ unusual stability enhancement” clearly exists for α = 0.8 or 1.0. The critical f at which the lifetime of the bond cluster is highest, falls about 0.2  Hz. When , there does not exist any clear “ unusual stability enhancement” .

Fig.  2.

	Figure Option ViewDownloadNew Window
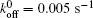
	Fig.  2. Variations of lifetime with fluctuation frequency when 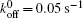(a), (b), and (c), with other parameters being kLR = 0.25  pN/nm, P0 = 70  pN, Pb = 3  pN, , and v0 = 100  nm/s.

The effects of P_b are shown in Fig.  3. We find that the “ unusual stability enhancement” of the bond cluster is also strongly affected by P_b. There is no clear “ unusual stability enhancement” when P_b = 1  pN, shown in Fig.  4(a). When P_b = 3  pN, the stability of the cluster is substantially enhanced for α = 1 or 0.8, with the critical f falling around 0.2  Hz. The comparison of Fig.  2 with Fig.  3 shows that the effects of increasing P_b on the enhancement may be equivalent to those of decreasing , which can also be inferred from Eq.  (2). These data suggest that the dissociation rate of a single bond has a strong effect of the “ unusual stability enhancement” of the bond cluster.

We then investigate the effects of some parameters in the binding rate of a single slip bond in Eq.  (3), i.e., , k_LR, and v₀. Effects of are shown in Fig.  4. When , there exists a relatively weak “ unusual stability enhancement”

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Variations of lifetime with fluctuation frequency for (a) Pb = 1  pN, (b) Pb = 3  pN, and (c) Pb = 6  pN, with other parameters being kLR = 0.25  pN/nm, P0 = 70  pN, 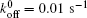, , and v0 = 100  nm/s.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Variations of lifetime with fluctuation frequency for (a) , (b) , and (c) , with other parameters being kLR = 0.25  pN/nm, P0 = 70  pN, , Pb = 3  pN, and v0 = 100  nm/s.

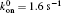
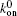
We also investigate the effects of the average value of the fluctuated force, P₀, as shown in Fig.  7. Though the “ unusual stability enhancement” occurs for α = 1 or 0.8 for all investigated values of P₀, with the critical f falling about 0.2  Hz, it appears to turn weaker at a higher P₀. It seems that the stability enhancement becomes more evident and the frequency range also becomes slightly broader, when the average force P₀ is lower. The effects of the total number of receptors on the stress fiber, N_R, or ligands on the surface of the substrate, N_L, are also investigated. In one case of our simulation, we let N_R = 80 and N_L = 120. In another case, we let N_R = 120 and N_L = 160. Our simulation results indicate that the difference among results of different sets of N_R and N_L are trivial.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Variations of lifetime with fluctuation frequency for (a) kLR = 0.1  pN/nm, (b) kLR = 0.25  pN/nm, and (c) kLR = 1  pN/nm, with other parameters being P0 = 70  pN, , Pb = 3  pN, , and v0 = 100  nm/s.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. Variations of lifetime with fluctuation frequency for (a) v0 = 30  nm/s, (b) v0 = 100  nm/s, and (c) v0 = 500  nm/s, with other parameters being kLR = 0.25  pN/nm, , Pb = 3  pN, , and P0 = 70  pN.

Fig.  7.

	Figure Option ViewDownloadNew Window
	Fig.  7. Variations of lifetime with cyclic frequency for (a) P0 = 60  pN, (b) P0 = 70  pN, (c) P0 = 80  pN, and (d) P0 = 100  pN, with other parameters being kLR = 0.25  pN/nm, , Pb = 3  pN, , and v0 = 100  nm/s.

Taken together, the above results show that the phenomenon of “ unusual stability enhancement” of bond cluster is quite robust in the simulations. Both dissociation rate and the binding rate of a single slip bond, and also the profile of the fluctuated forces, such as the average value of bond force, can have a strong effect on the “ unusual stability enhancement” . It is also shown that the stability enhancement often occurs at a fluctuation frequency around a few tenths of 1  Hz and a relatively large fluctuation amplitude. When looking at the evolution of the displacement at the right end of the fiber, we find the fiber often moves back and forward for multiple times when the “ unusual stability enhancement” occurs.^[21]

Fluctuated traction forces within focal adhesions may be induced by applying cyclic stretches to substrates to which cell adheres. The previous analysis indicated that the traction force would then fluctuate around a homeostatic value with the same frequency as the applied stretches under this condition.^[23] The model prediction^[23] also suggested that such fluctuation forces may induce the instability of focal adhesions so that focal adhesions tend to slide or rotate toward a direction in which they are stablest, which is in consistence with experimental results.^[11] To validate this model prediction, Chen X and Chen B^[21] represented a single focal adhesion with a cluster of slip bonds and directly simulated the stability of the bond cluster under fluctuated forces with a coupled finite element analysis and Monte Carlo method. The simulation results showed that the bond cluster did indeed often become unstable under fluctuated forces, suggesting the possible role of slip bonds in cellular reorientation under cyclic stretches.^[21]

In the simulation by Chen X and Chen B, ^[21] however, an unusual case was also reported, where fluctuated forces with very low fluctuation frequencies and large fluctuation amplitudes led to a very long lifetime of the cluster. Such an “ unusual stability enhancement” occurring only at relatively large stretch magnitude is quite surprising and difficult to explain.^[21] For example, the system under investigation by Chen X and Chen B^[21] might bear some similarities to a fatigue test. In light of fracture theory, the lifetime of a fatigue crack would decrease with the stretch amplitude instead, according to the well-known Paris’ s law.^[22] In the study of fatigue cracks within rubbers, Lake and Thomas^[31] also demonstrated that there exists a critical tearing energy, below which crack does not grow. The critical tearing energy was shown to correspond to the energy required to rupture the polymer chains lying across crack growth path.^[31] Thus, the prediction of the conventional fracture theory may contradict to this “ unusual stability enhancement” , though a distinct feature of the system under current investigation is stochastic.

To understand whether such an “ unusual stability enhancement” is robust and what it depends on, we carry out parametric studies on the stability of a cluster of slip bonds under fluctuated forces in the present work. Our intensive simulation results indicate that the “ unusual stability enhancement” is robust and often occurs when the fluctuation frequency is relatively low and the fluctuation amplitude is relatively high. However, the exact frequency or amplitude at which it occurs depends on the stochastic features of a single bond, and the profile of the fluctuated forces as well. The simulation indicates that the “ unusual stability enhancement” often occurs at a fluctuation frequency around a few tenths of 1  Hz and a relative stretch amplitude over ∼ 0.5.

From the evolution of the displacement at the end of the fiber, we find that the fiber often moves back and forward a very short distance for many rounds when the “ unusual stability enhancement” occurs.^[21] It appears that the phase with lower force values during the fluctuation would facilitate the rebinding of dissociated bonds, which might induce the “ unusual stability enhancement” . This makes us postulate that a part of input mechanical energy might be able to be utilized to re-heal the cracked interface, when the adhesive bonds are stochastic in feature. This new viewpoint in physics has not been considered in the conventional theory framework of fracture theory on fatigue, which may account for the contradiction of current results against the prediction of conventional fracture theory.

In understanding how cell on elastic substrates tends to migrate toward regions of higher stiffness, traction forces within single mature focal adhesion were measured with traction force microscopy.^[6] It was revealed that the traction force within an individual focal adhesion may fluctuate with a relatively low fluctuation frequency, ∼ 0.1  Hz, and a relatively large fluctuation amplitude, ∼ 0.5.^[6] It was also suggested that individual focal adhesions used such fluctuated forces to dynamically sense substrate stiffness to guide durotaxis.^[6] Since the reported fluctuated force within focal adhesions also has a relatively low fluctuation frequency and relatively large fluctuation amplitude, ^[6] we then suggest that such a fluctuation of traction force within a focal adhesion might help enhance its stability. In this way, it can be safe when the force on a focal adhesion is fluctuated to dynamically sense substrate stiffness.^[6]

Through intensive simulations, we studied the “ unusual stability enhancement” of a bond cluster under fluctuated forces. Based on detailed parametric studies, we conclude that the “ unusual stability enhancement” is robust. We find that it often takes place at a relatively low fluctuation frequency and large fluctuation amplitude, depending on the intrinsic properties of bonds, such as dissociation rate and binding rate, as well as the profile of the fluctuated force, such as the average value of bond force. Since it was recently found that the traction forces with a focal adhesion can coincidentally fluctuate at a frequency about 0.1  Hz with a relatively large fluctuation amplitude, ^[6] we then suggest that the fluctuation of traction force within a focal adhesion might help enhance its stability in this way.