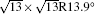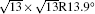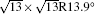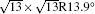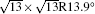†Corresponding author. E-mail: clin@ams.k.u-tokyo.ac.jp
‡Corresponding author. E-mail: n-takagi@k.u-tokyo.ac.jp
*Project supported by the Ministry of Education, Culture, Sports, Science and Technology (MEXT) through Grants-in-Aid for Scientific Research (Grant Nos. 24241040 and 25110008) and the World Premier International Research Center Initiative (WPI), MEXT, Japan.
The electronic structures of monolayer silicenes (4 × 4 and
Silicene, the two-dimensional (2D) honeycomb lattice of Si atoms, has received a lot of attention because it shares remarkable properties with graphene. Density functional theory (DFT) calculations[1, 2] have demonstrated that freestanding silicene takes a buckled structure where two Si atoms in the unit cell are displaced in the opposite directions perpendicular to the basal plane. In spite of the buckling, silicene hosts Dirac fermions similarly to graphene. The combination of the Dirac fermion characteristics with sizable spin-orbital coupling (SOC) of Si adds exotic properties to silicene.[3– 6] An energy gap opens at the Dirac cone where two linear bands cross at the Fermi level, and topologically protected states emerge at the edges of 2D silicene. This indicates that silicene is promising as a material for realizing the theoretical prediction of Kane and Mele.[7] Besides, silicene is expected to be compatible with the current process technologies to fabricate electronic devices on Si platform.
In the last few years, silicene has not been only in the theoretical calculation; it has successfully been synthesized on many different substrates, such as Ag (110), [8] Ag (111), [9– 11] Ir (111), [12] ZrB2-covered Si (111), [13] and MoS2 crystal, [14] of which, the silicene synthesized on Ag (111) is investigated most.[9– 11, 15– 39] Several phases such as 4 × 4, 


The whole experiments were performed in an ultra-high vacuum chamber with a base pressure less than 1 × 10− 10 Torr (1 Torr = 1.33322 × 102 Pa). To grow silicene on Ag (111) substrate, Si atoms were deposited onto the clean Ag (111) substrate in a constant rate of 0.03 ML/min (1 ML = 1 × 1015 atoms· cm− 2 from a heated (> 1100 ° C) Si wafer. The Ag (111) substrate was cleaned by repeated cycles of Ar + sputtering and annealing at 500 ° C. The trick to crystalize silicene is the precise control of the Ag (111) substrate temperature. In our experiments, the temperature was kept at 260 ° C during the deposition. After sample preparation, the STM and STS measurements were carried out at 6 K.
The DFT calculations were carried out by the plane-wave-based Vienna Ab initio Simulation Package (short as VASP)[41, 42] with the projected augmented wave (PAW)[43] potentials in the generalized gradient approximation (GGA). The exchange– correlation functional of Perdew– Burke– Ernzerhof (PBE)[44] was used. The kinetic-energy cutoff for the plane-wave basis was set to be 400 eV. The silicene grown on Ag (111) was modeled by using a supercell, which consists of a silicene layer on a 5-layer Ag slab with a vacuum of ∼ 18 Å thick along the surface normal. The supercell used for the 4 × 4 (
Figure 1(a) shows an STM image of monolayer silicene grown on Ag (111). Both 4 × 4 and 

Figure 1(c) shows the typical STS spectra acquired on 4 × 4 and 



In contrast, the unoccupied electronic states in higher energy range are different. Figure 1(d) shows the dZ/dV spectra acquired in a bias range from 1.0 V to 3.8 V. In the
Z– V spectrum, the displacement of the tip (Z) is measured as a function of bias voltage (V) applied to the STM junction with holding the feedback loop on. The tip promptly retracts from the surface to keep the tunneling current constant when the density of states increases at certain voltages. In other words, the displacement of the tip depends on how the density of states varies with energy. By differentiating the Z– V curve, peaks appear at the voltages where the density of states is relatively high. Therefore, the dZ/dV spectrum is basically proportional to the density of states; it reveals the electronic structure as well as the conventional STS spectrum.[45– 47] The spectra shown here are obtained by a lock-in technique with a modulation voltage of 14 mV at 512 Hz. A sharp peak appears at 2.95 V in 4 × 4 phase while a broad peak around 2.70 V and a shoulder near 3.40 V are observed for 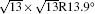
To understand the variations in the electronic structures of two phases, the electronic band structures are calculated for both 4 × 4 and 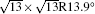
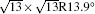

overlap with the bands derived from Si. (ii) The bands relevant to the Si 3pz orbital hybridize with the substrate Ag states and their contributions are scattered.
The band structures of the 4 × 4 and 
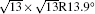
One can easily see the difference in band structure between the 4 × 4 and 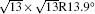


The difference in geometric configuration between 4 × 4 and 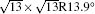





Table 1. Structural parameters of the 4 × 4 and  |
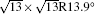
Before closing discussion, we come to discuss the geometric structure of 



Silicene has been acknowledged as a new allotrope of Si. Comparing with graphene, silicene is more flexible in structure. Different buckled configurations are found from the silicene synthesized on Ag (111) surface. By the combination of STS measurements and DFT calculations, we successfully find the difference in electronic structure between the 4 × 4 and 

Computation in this work was performed by using the facilities of the Supercomputer Center, the Institute for Solid State Physics, University of Tokyo.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|