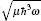†Corresponding author. E-mail: ybzhang@sxu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11234008 and 11474189), the National Basic Research Program of China (Grant No. 2011CB921601), and the Program for Changjiang Scholars and Innovative Research Team in University, China (Grant No. IRT13076).
A more reasonable trial ground state wave function is constructed for the relative motion of an interacting two-fermion system in a one-dimensional (1D) harmonic potential. At the boundaries both the wave function and its first derivative are continuous and the quasi-momentum is determined by a more practical constraint condition which associates two variational parameters. The upper bound of the ground state energy is obtained by applying the variational principle to the expectation value of the Hamiltonian of relative motion on the trial wave function. The resulted energy and wave function show better agreement with the analytical solution than the original proposal.
Tremendous progress in cooling, trapping, and manipulating ultracold samples makes it possible to experimentally study few-body phenomena in trapped atomic and molecular systems with precise control.[1– 6] The study of trapped few-atom systems provides a bridge between small and large systems and the treatment of such mesoscopic systems is complementary to the interpretation derived within effective many-body frameworks. Systems made of just two interacting atoms are especially relevant due to its role as building blocks of many-body strongly correlated states. Two-body system with tunable interactions has been realized in the Heidelberg experiment[2, 3] using two fermionic 6Li atoms in the ground state of a potential created by an optical dipole trap. In this experiment, the interaction energy of two distinguishable fermions as a function of the interaction strength has been measured showing the experimental capability to simulate strongly correlated few-body quantum systems. An exceptional property of the two-body interacting system is that there exists an analytical solution for arbitrary values of the interparticle interaction.[7– 13] For the strongly interacting limit, the exact results has been generalized to the model of other external potential.[13, 14] A theory for the tunneling of one atom out of a trap containing two interacting cold atoms is developed by introducing the quasi-particle wave function.[15, 16] Unfortunately, no theoretical solution is available for more complex systems even if one more atom is included.
It is thus of interest to seek for some approximation methods which may potentially be generalized to more than two particles. Reference [17] provides such an example, which calculated the ground-state energy of the relative motion of a system of two fermions with spin up and spin down interacting via a delta-function potential in a one-dimensional (1D) harmonic trap. The authors divided the relative coordinates space into three regions and established a trial ground state wave function according to the Bethe-ansatz solution[18, 19] for a system with delta-function interaction and the ground state wave function of harmonic potential. They directly applied the periodic boundary conditions to obtain the Bethe ansatz equation, which was taken as the constraint condition for quasi-momentum. By analyzing solution of the Bethe ansatz equation, we know that the possible values for the quasi-momenta k depend on the value of c.[20– 26] For the repulsive case (c > 0), only real values of k are ground-state solutions of the Bethe ansatz equation. For the attractive case (c < 0), only the purely imaginary numbers k satisfy for the ground state. For both cases they found the numerical minimization of expectation value of the ground state energy by introducing two variational parameters. This work provides a starting point for the investigation of more complex few-body systems where no exact theoretical solution is available.
In this paper we improve the trial ground state wave function proposed in Ref. [17] from two aspects. Firstly not only wave function but also its derivative are continuous at the boundaries, which avoids introducing the discontinuity of the first derivative of the wave function for regular potential. Secondly instead of using Bethe ansatz equation as the constraint condition, we find a more practical constraint condition for the quasi-momentum which incorporates the two variational parameters and the contact interaction strength. There, the solutions of the constraint condition no longer depend on the sign of c. This approach may be employed to deal with the interacting two-atom system trapped in more general external potentials.
The paper is organized as follows. In Section 2, we introduce the modified trial ground state wave function for the system of two interacting fermionic atoms. At the boundaries both the wave function and its first derivative are continuous and we obtain a similar constraint condition for the two variational parameters. Then the variational principle is applied to the expectation value of the Hamiltonian of relative motion on the conjectured wave function in Section 3. In Section 4. Our results are compared with the analytical result obtained in Refs. [7] and [8] and the approximate result obtained in Ref. [17]. In addition the density distributions for various interaction constants also show good agreement with the analytical solution. We conclude our results in Section 5.
We shall consider the same system of two interacting fermionic atoms with mass m loaded in a harmonic trap of frequency ω as in Ref. [17]. The Hamiltonian can be formulated as
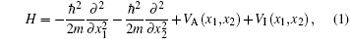
where VA(x1, x2) is the trapping potential for atoms located at x1 and x2
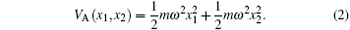
The interaction potential VI is assumed to be s-wave contact potential represented by a delta-function
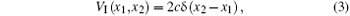
where the interaction strength c can be tuned via magnetic Feshbach resonance from − ∞ to + ∞ .
Introducing the center-of-mass and relative coordinates x = x1 − x2, X = (x1 + x2)/2 allows us to decompose the Hamiltonian (1) into the center-of-mass part
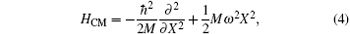
and relative motion part

The Hamiltonian of the center-of-mass is nothing but a simple harmonic oscillator with total mass M = 2m, while the relative part describes an oscillator with reduced mass μ = m/2 and a delta potential well/barrier in the trap center. The latter has been exactly solved in Ref. [7].
In Ref. [17] the authors built a variational trial wave function ψ (x, {α , L}) based on the Bethe ansatz solution of two particles and it was shown that applying the same principle for a large number of fermions is possible. The parameters α and L controls the decay of the trial function outside the trap and the region where the decay occurs. Minimizing the expectation value of the Hamiltonian Hrel on the conjectured wave function ψ (x, {α , L}) by setting the derivatives with respect to these two parameters zero gives the upper bound of the ground state energy of the system
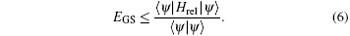
The trial wave function ψ is continuous in Ref. [17], however, the first derivatives of the wave function develop an unphysical discontinuity at x = ± L. We know from basic quantum mechanics that in matching the wave functions in different regions the wave function ψ is always continuous and the first derivative dψ /dx is continuous except at points where the potential is infinite, i.e., δ potential. In our problem there do not exist such δ potential points at x = ± L hence discontinuity of the first derivative there should be excluded. As we shall see below a simple improvement of the trial wave function will help us get rid of this dilemma and the resulted ground state energy matches the analytical result even better.
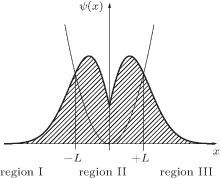
In the following we introduce the variational ansatz and the modification of the trial ground state wave function. As shown in Fig. 1, the wave function is continuous and it’ s derivative is also continuous, which is much closer to the real wave function.
How do we build the trial ground state wave function for the two-body problem of Hamiltonian Hrel? The space is divided into three regions by the parameter L. The wave functions in the regions I and III are chosen as eigenstates of 1D harmonic oscillator center at x = 0, instead of at x = ± L as done in Ref. [17], ψ I and ψ III have the form of the Gaussian with the parameter α . In the regions II, i.e., in the vicinity of the δ potential center, the contact interaction term plays the dominant role and the harmonic potential can be neglected. The wave function takes the form of two distinct fermions with a contact interaction. Formally, we assumes the trial ground state wave function as the following configuration:
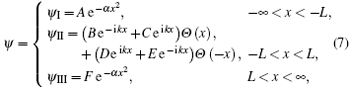
where Θ is the Heaviside step function
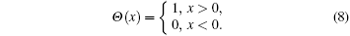
The remaining work is to match the wave functions in different regions through the boundary conditions. In region II, the continuity of the wave function ψ II at x = 0 gives the following coefficient relation:
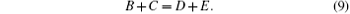
By integrating the eigenequation Ĥ ψ II = Eψ II from the negative infinitesimal to the positive infinitesimal, we do find a jump of the first derivative of wave function at x = 0
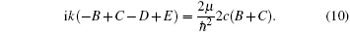
Because the potential is axially symmetric, the ground state wave function must be spatially symmetric and has zero nodes, so

According to the above three equations, we obtain
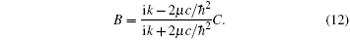
At x = − L or x = L, the wave function is continuous, which means
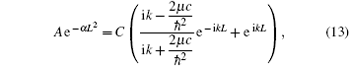
and the first derivative of ψ is continuous too, we obtain
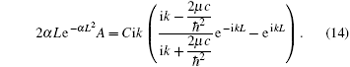
The combination of Eqs. (13) and (14) leads us to a constraint condition
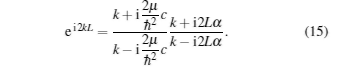
This equation plays a similar role as that of Bethe ansatz equation. It is, however, irrelevant with the boundary conditions (periodic or open) for the two-fermion system which should always be chosen before one deals with the exactly solvable models. In this way, we avoid artificially imposing the periodic boundary condition onto the system. And we find no obstacles to generalize this constraint condition to N fermions following a similar scheme as in the Appendix of Ref. [17].
On the basis of above restrictions to the coefficients, we obtain the following trial ground state wave function subject to normalization:
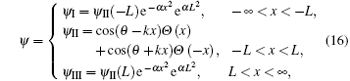
where θ satisfies the following relation:
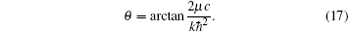
This trial ground state wave function, composed of pure elementary functions, offers convenient analysis due to the continuity of both its first derivative and itself. We schematically show the configuration of the potential and the wave functions in Fig. 1, which join each other smoothly at the boundaries for all three regions.
We choose α and L as our variational parameters and aim to find the least possible value of the ground state energy on the trial wave function for different interaction strength c subject to the constraint condition (15). Contrary to the original proposal (Eq. (3.2) in Ref. [17]), in our scheme, both variational parameters α and L enter into the constraint condition, which determines the quasi momentum k. To apply the variational principle, we need to compute the normalization factor of the wave function, which yields
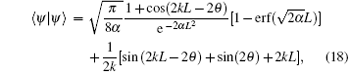
where the error function erf(x) is defined as
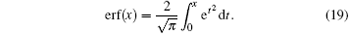
Moreover, the expectation value of Hrel on the ground state (16) is calculated as
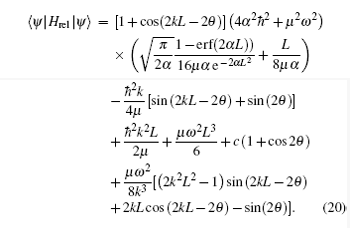
It is interesting to consider first the limiting case of L → 0, c → 0, that is, a simple harmonic oscillator. Accordingly the upper bound for the ground state energy (6) reduces to
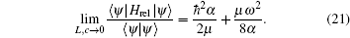
The minimum value of the energy can be found by setting the first derivative with respect to α to zero. We find the extreme value of α , which indicates the decay of the trial function, to be α * = μ ω /2ħ , such that
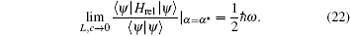
In this case we recover precisely the ground state energy of the simple harmonic oscillator.
For the model system, the constraint condition (15) for the trial wave function reduces to

Putting this back into inequality (6), we sweep over all values of L and k for each assigned c and minimize the expression (6) numerically. We call the extreme parameters L* and k* when the minimization point has been reached. In this way, we determine the ground state energy of the two-fermion system as a function of the coupling c via the variational principle, for both repulsive and attractive interactions. The result is depicted in Fig. 2 in terms of the physical variables ε and a1D, which are related to the energy EGS and interaction strength c through
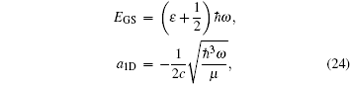
and the value of ε is determined by the following implicit equation:
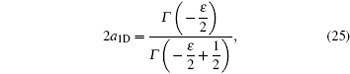
where Γ (x) is the complete gamma function. We notice that by combining the variational principle and continuity of the wave function derivatives, a better agreement is achieved between this analytical result (black dotted line in Fig. 2) and our result (red solid line in Fig. 2(b)) than that obtained with the Bethe ansatz equation as constraint condition (blue solid line in Fig. 2(a)). In the repulsive case, the modified variational curve lies exactly on the top of analytical one and the effective matching range of the approximation in the attractive case is also much wider than the original proposal.
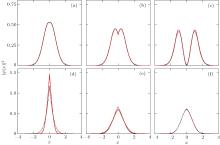
Inserting the parameters L* and k* back into Eq. (23), we obtain the corresponding α * . The trial wave function (16) is determined by these parameters L* , α * , and k* for each value of c. The probability densities of the trial ground state wave function in the relative coordinate are illustrated in Fig. 3 over the whole range of c. It reveals that our variational wavefunctions near perfectly match the analytical ground state wave functions of the relative motion Hamiltonian Hrel, which is Ref. [7] (see Figs. 3(a) and 3(b)), which is[7]
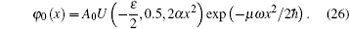
The extension to weakly attractive case is possible (Figs. 3(e) and 3(f)), but not too far. If the interaction is negative, the ground state is the McGuires cluster state, [27, 28] which is a bound state and would decay quickly via molecular channels. We see that whereas our variational theory yields surprisingly accurate energies, the wave functions are notoriously poor for finite attraction (Fig. 3(d)).
In conclusion, we have found a much better trail wave function that approximates the ground state energy of two interaction fermions in a 1D harmonic trap via variational principle with the constraint conditions of the continuity of both wave function and its derivative. This provides a modified scheme which enables us to get rid of the idealized periodic boundary condition in the central region − L < x < L. Instead, we connect the wave functions and derivatives at x = ± L by simple quantum mechanics rules. A constraint condition is obtained to determine the quasi momentum, under which the variational principle is applied to minimize the ground state energy. This offers a new approach to solve the few-body problem and the better agreement between our results and the analytical solution shows that it is convincing to extend our method to many-body systems, which arouse experimental interest.[29]
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|