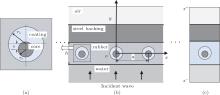
Figure  1(a) shows the cross section of one LRS unit, i.e., the heavy core (with radius r_c) non-coaxially coated by soft rubber (with outer radius r_s). The longitudinal eccentricity between the heavy core and soft rubber is e. The infinite long cylindrical LRSs are arranged in the rubber matrix along the x direction with the single period a, and the axis of the cylinder is parallel to the z direction as shown in Fig.  1(b). The thickness of the material is h, a plane longitudinal incident wave is from the semi-infinite water and perpendicular to the xoz plane. The viscoelastic panel is bonded to a steel slab followed by semi-infinite air. The whole structure can be regarded as a sequence of different layers perpendicular to the y direction.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) Cross section of one LRS unit, i.e., a heavy core with radius rc and an eccentrically coated rubber layer with outer radius rs and a longitudinal eccentricity e. (b) Schematic diagram of the absorption structure and steel backing. (c) Schematic description of one Bloch unit cell.

Because of the invariance in the z direction, the original three-dimensional (3D) structure can be simplified into a 2D model as shown in Fig.  1(b). According to the Bloch condition, the displacement u in solid and the sound pressure p in water can be incorporated into the following form:

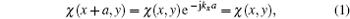
where a is the period (or lattice constant) along the x axis and the wave vector in the x direction is k_x = 0. Therefore, we can simplify the absorption problem of the infinite panel into the analysis of one Bloch unit cell as shown in Fig.  1(c). The unit cell is divided into four parts, in which, the first part is semi-infinite water domain, the second part is of viscoelastic material, and the other two parts are steel backing and semi-infinite air domain, the two semi-infinite domains are limited by the surface s⁻ and s⁺ . Omitting the time dependence e^{− jω t}, the external incident wave can be written as

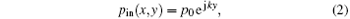
where the wave number k = ω /c, with c being the sound speed in water, ω the angular frequency, and p₀ is the magnitude of incident wave.

In the domain below the s⁻ surface, the total wave field, including both the incident wave and the reflected wave, can be written in a general form:

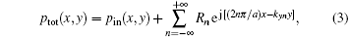
where .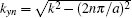

Analogously, in the domain above the s⁺ surface, the transmitted wave can be written in a general form:

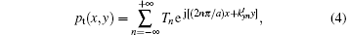
where

with k′ being the wave number in air.

The finite element description equations for the fluid-structure interaction of a single cell are written as an incorporated matrix form^{[9, 23]}

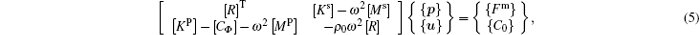
where ρ ₀ is the fluid density, ω denotes the angular frequency, [K] and [M] are, respectively, the structure stiffness and coherent mass matrices, the superscript s and p denote the solid and fluid component, respectively, [R] is a connectivity matrix that shows the coupling between the structure and the fluid and also relates to the kinematical and dynamical interface continuity equations, {F^m} denotes the nodal value of the applied force, [C_Φ ] and {C₀} contain the nodal values of the pressure normal gradients on the fluid domain boundaries of surface s⁻ and s⁺ .

Combining the boundary condition Eq.  (1), and solving Eq.  (5), one can obtain displacement u in solid and pressure p in fluid. Then according to the continuity of the normal velocities at the interfaces s⁻ and s⁺ , the unknown coefficients R_n and T_n of the harmonics can be obtained. The energy reflectance and transmittance are defined as follows:

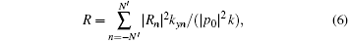
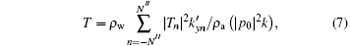
where N′ and N″ are the orders of the occurring reflection wave and transmission wave, ρ _w and ρ _a are the densities of water and air, respectively. For energy conservation, the absorption coefficient is defined as follows:

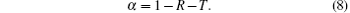
The thickness of the viscoelastic material h is 10  mm, the lattice constant a is 20  mm, the radius of coating layer r_s is 4  mm, the radius of heavy core r_c is 2  mm, and the distance from the center of the coating layer to the interface is h/2. The elastic parameters of the components are listed in Table  1. To simplify the problem, it is assumed that the viscoelastic properties of the material do not vary with frequency. The unit cell is meshed with triangular elements. For each material domain, the discretization ensures that the largest length of elements is smaller than a quarter of transverse wavelength in respective material.^[9] The boundaries between different material domains meet the displacement continuity conditions.

Table 1.

Table 1.

Table 1. Material properties of the LRSM panel. Material Young ’ s modulus/MPa Damping factor Poisson’ s ratio Density/(kg/m3) Rubber matrix 30 0.5 0.497 1100 Coating rubber 0.5 0.3 0.49 1100 Steel core 2.05× 105 0 0.28 7890

Table 1. Material properties of the LRSM panel.

Figure  2(a) shows the comparison among the absorptances of different values of longitudinal eccentricity e of the heavy core in a frequency range of 500  Hz– 3000  Hz. Here the values of e are chosen to be 0  mm, 1  mm, and 2  mm assigned as position 1, 2, and 3 respectively. It is shown in the figure that the core position has a considerable influence on the absorption performance of the viscoelastic panel. By changing the eccentricity of the core in LRS, two different types of absorptance curves are found. For positions 1 and 2, in the absorptance spectrum there appear apparent absorption peaks around 1650  Hz and 1800  Hz respectively. For position 3, there are two absorption peaks near 1500  Hz and 2250  Hz. Comparing the three absorption curves in detail, one can find that there are few changes in the absorptance at the frequencies below 1500  Hz with increasing the longitudinal eccentricity e, however, the absorptances above 1500  Hz becomes gradually better.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. (a) Comparison among the absorptances for three core positions. The dot– dashed line, the dashed line, and the solid line represent positions 1, 2, and 3, respectively. (b) Valid absorption (with absorptance above 0.8) frequency band (VAFB) varying with longitudinal eccentricity e.

Figure  2(b) shows the variation of valid absorption (with absorptance above 0.8) frequency band (VAFB) with eccentricity e. It can be seen that with increasing the eccentricity e, the lower frequency limit of the VAFB changes little, however, the upper frequency limit significantly increases. For position  3 (e = 2  mm), the upper limit frequency of the valid absorption band increases from 2100  Hz to 3000  Hz compared with that of position 1 (e = 0  mm). Thus, the VAFB of the viscoelastic panel becomes gradually broader as e increases.

In order to clarify the mechanism for the influence of core position on the sound absorption of the viscoelastic panel, we first calculate the frequency-dependent average difference of the longitudinal displacement (ADLD) between the upper surface and lower surface of the viscoelastic panel, by using the method in Ref.  [12],

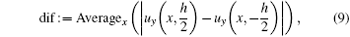
where Average_x means calculating the average value along the x direction, u_y denotes the y component of the displacement of the viscoelastic panel. Figure  3 shows the average displacement-difference spectra for different core positions. It can be seen that each of all curves has a displacement-difference peak near 1450  Hz, and the peak amplitudes are almost unchanged. It suggests that the largest overall deformation occurs at around 1450  Hz for all three viscoelastic panels with different core positions.

Fig.  3.

	Figure Option ViewDownloadNew Window
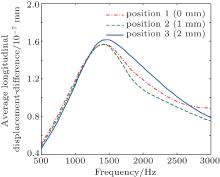	Fig.  3. Variations of average longitudinal displacement-difference spectra with frequency for core positions 1, 2, and 3.

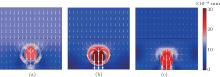
Furthermore, figure  4 shows the displacement fields of both the viscoelastic panel and the steel backing at 1450  Hz for the three different core positions. It shows that the displacement fields of the viscoelastic panel for different core positions follow the same pattern which can be called overall resonance mode (ORM).^{[8, 10]} The steel slab and the bottom area (near the steel slab) of the viscoelastic panel show the larger displacement amplitude than that of the other portion in the panel. The displacement around the LRS changes with core position, however, the amplitude is much less than the steel slab. It suggests that the resonance absorption of the viscoelastic panel is determined mainly by the vibration of the steel backing, but not the LRSs. Therefore, as the eccentricity of the heavy core varies, there occur few differences in the sound absorption performance (around 1450  Hz in Fig.  2(a)) of the viscoelastic panel.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. The displacement fields of both the viscoelastic panel and the steel backing at 1450  Hz for core positions 1 (a), 2 (b), and 3 (c)). The linear color bar indicates the magnitudes of the total displacements of the structures. The arrows denote the displacement vectors of the nodes of the structures, and the arrow length is scaled by the displacement amplitude.

Comparing Fig.  2(a) with Fig.  3, one can see that only for the core position 3, the first absorption peak (near 1500  Hz) of the viscoelastic panel can agree well with the peak frequency (near 1450  Hz) of the ADLD. For positions  1 and 2, their absorption peaks occur near 1650  Hz and 1800  Hz respectively. Figures  5(a) and 5(b) show the displacement fields of the viscoelastic panel and the steel slab corresponding to these two absorption peaks. One can see that the core of LRS vibrates as a whole and has more obvious displacements than the steel slab and the rubber matrix. It shows that the LRS exhibits a rigid body resonance^{[9– 11]} which we refer to as core resonance mode (CRM). Figure  5(c) further shows the displacement field of the viscoelastic panel at the second absorption peak (near 2250  Hz in Fig.  2(a)) for position  3. It shows that the LRS has a similar displacement pattern to the cases of positions  1 and 2, however, the displacement amplitude of the steel slab and the rubber matrix are smaller. Considering all three displacement fields in Fig.  5, it can be found that at the absorptance peak frequencies for different core positions, the displacement amplitudes in the steel slab and the rubber matrix decrease gradually with increasing the eccentricity e. Thus, for positions  1 and 2, because of the coupling effect between the CRM and ORM, in the absorptance spectra there occurs first absorption peak that is broader around each of 1650  Hz and 1800  Hz respectively, thereby leading to the peak-frequency difference between the absorptance spectrums and the ADLD. From another perspective, the steel core in conjunction with its coating layer can be considered as a spring-and-mass system.^[1] With increasing the longitudinal eccentricity e of the heavy core, the effective stiffness of the coating layer of the LRS increases, then the CRM shifts toward higher frequency. In consequence, the VAFB of the panel can be broadened gradually. For example, the CRM with largest eccentricity (position 3) shifts to 2250  Hz so that it can decouple with ORM (near 1450  Hz). It results in two separate absorption peaks and then a broad VAFB forms.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Displacement fields of both the viscoelastic panel and the steel slab corresponding to the absorption peaks of (a) 1650  Hz, (b) 1800  Hz, and (c) 2250  Hz, respectively for core positions 1, 2, and 3.